HDPE 瓶顶部负载仿真分析
吴子鸣,吴映桐,孙一鸣,张立军,王立军,2,宋海燕,2
(1.天津科技大学 轻工科学与工程学院,天津 300457;2.中国轻工业食品包装材料与技术重点实验室,天津 300457)
高密度聚乙烯(High Density Polyethylene,HDPE)是目前使用量较大的聚合物材料之一。HDPE无毒、无味,具有较高的耐酸、碱腐蚀性和良好的力学性能,通常用于制造牛奶、药品或油的容器。中国2021 年生产了2 842.98 万t 液态奶制品,产量比上一年增长了 9.7%[1]。牛奶产量的增长将带来更大的HDPE 瓶使用量,这些HDPE 瓶在运输和交付过程中会受到较大的外界载荷,因此,它们需要强大的力学性能。然而,为了提高HDPE 瓶的可回收性,HDPE瓶也应当有低质量、易粉碎的特点。因此,在设计HDPE 瓶时,既需要较高的强度和刚度,也要综合考虑瓶体的厚度,避免材料浪费和环境污染。
实际生产过程中,改变吹瓶工艺耗时且成本高昂,实验研究不适用于塑料瓶的改进。因此,通常选择数值模拟的方法来改进塑料瓶,而有限元建模(Finite Element Modeling,FEM)更是首选。Huang等[2]针对2.8 L 的HDPE 牛奶瓶,设置瓶身和瓶底两部分厚度并进行顶部负载仿真实验,轻质设计后质量减少了21.4%。Keawjaroen 等[3]利用卷积神经网络设计出理想的HDPE 瓶,并对设计出的HDPE 瓶进行顶部负载测试与仿真实验。目前,针对HDPE 瓶的仿真研究较少,大部分的工作针对了PET 瓶的跌落与静压。李强等[4]对考虑了流固耦合作用的PET 瓶跌落过程进行了数值模拟,并研究了储液量、跌落角度对冲击应力的影响。Hu 等[5]根据顶部负载的应力云图优化PET 瓶的结构设计,降低了PET 瓶的质量。Masood等[6]阐述了一种用PET 材料替代PC 材料制作饮水桶的替代方案,并对PET 饮水桶进行了建模和数值仿真。Demirel 等[7]研究了瓶底几何形状对PET 力学性能的影响,并通过数值模拟的方法计算了改底后PET瓶的应力。宋卫生等[8]详述了爪瓣式瓶底结构对碳酸饮料瓶力学性能的影响,并使用有限元计算了饮料瓶充气破裂过程中的最大应力。实际应用过程中,塑料瓶的厚度远小于瓶的表面积,计算量较少的壳体模型是瓶体有限元仿真的首选。研究吹塑成型的塑料瓶时,大部分的数值模拟工作针对PET 瓶瓶坯的尺寸设计,不等壁厚的吹塑瓶有限元模型被少部分学者用于进一步的数值验证[9]。胡青春等[10]、刘良先等[11]和Woo 等[12]通过数值模拟的方法改进瓶坯的结构,得到改善了材料分布和增强了力学性能的PET 瓶。Siripath 等[13]仿真分析了吹塑的温度和时间对HDPE瓶壁厚的影响,最终壁厚的误差为0.196 22%。Nguyen等[14]描述了吹塑过程中PET 的各向异性对PET 力学性能的影响,并根据PET 瓶的顶部负载仿真实验验证了数据模拟的结果。等壁厚的壳体有限元模型被大量应用于塑料瓶瓶体的力学仿真实验,这与实际的吹塑瓶壁厚分布存在较大的差异。因此,本文通过建立不等壁厚的HDPE 瓶壳体有限元模型,减少传统瓶体建模方式带来的计算结果的误差,并仿真分析HDPE瓶瓶体的厚度组成对整瓶顶部负载能力的影响。
1 有限元模型
1.1 HDPE 瓶有限元模型的建立
重力作用下,盛装过牛奶的HDPE 瓶会发生弯曲变形,使用迅恒手持三维扫描仪,3D 扫描得到准确的HDPE 瓶点云模型,模型共包含1 346 004 个小三角形面片。使用Geomagic Studio 软件合并点云模型至49 个曲面片,并导出HDPE 瓶的数字模型。通过Solidworks 软件合并曲面片成1 个面组,最后导出HDPE 瓶几何模型。HDPE 瓶满口容积为2 L,实际灌装牛奶1.89 L,其主要尺寸如图1 所示。
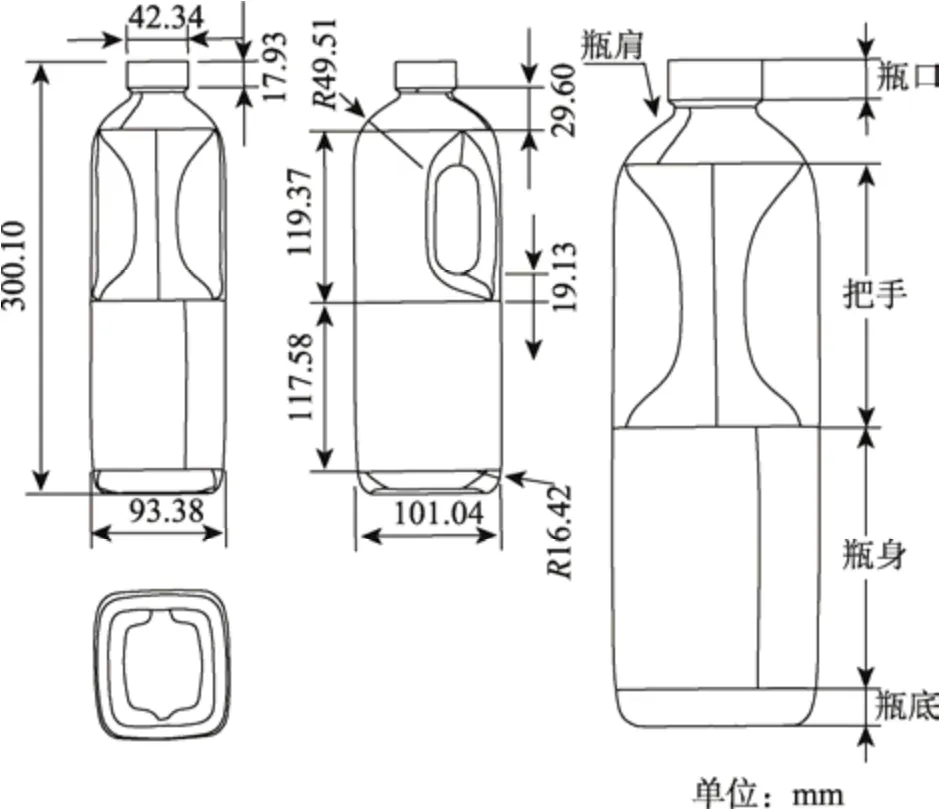
图1 HDPE 瓶主要尺寸Fig.1 Main dimensions of HDPE bottle
测量HDPE 瓶的刨面厚度得到瓶体各部分的平均壁厚。HDPE 瓶瓶口及螺纹部分平均厚度为1.50 mm,并采用圆柱壳替代原有瓶口结构。瓶肩部分平均厚度da=1.54 mm、把手部分平均厚度db=1.10 mm 以及瓶身部分的平均厚度dc=1.05 mm。整个瓶底部分划分为3 个区域:瓶底的触地面区域、瓶身部分至瓶底触地面的弧形过渡区域和瓶底的底面区域,其平均厚度分别为1.50、1.70 和1.90 mm。
采用有限元软件ABAQUS 进行数值仿真。参考塑料拉伸性能的测定标准[15],在HDPE 瓶的瓶体上切割HDPE 片材,进行拉伸速率分别为5、100 和500 mm/min的拉伸实验。拟合HDPE 材料的弹性模量,并将工程应力–应变曲线转为真实应力–应变曲线,在ABAQUS 中构建与应变率相关的HDPE 材料模型。HDPE 本构模型如图2 所示,其密度为913.85 kg/m3,弹性模量为559.415 MPa,泊松比为0.419[2]。设计牛奶瓶时,瓶盖的尺寸及螺纹拥有独立的设计标准,瓶口的尺寸设计需要参考瓶盖的标准。有限元计算时,瓶口的螺纹曲面微小复杂,占用较多的计算量。因此,使用柱形面替代原瓶口撑环及螺纹,并且忽略瓶口螺纹对HDPE 瓶力学性能的影响。
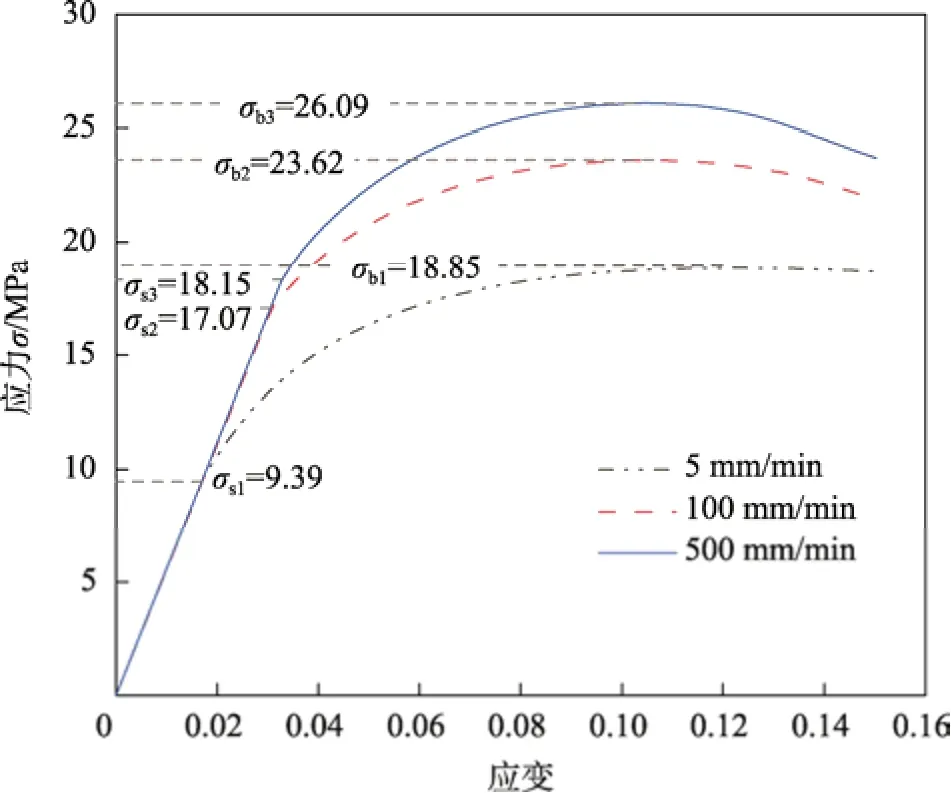
图2 HDPE 本构模型Fig.2 Constitutive model of HDPE
1.2 网格与边界条件
经网格无关化验证,对HDPE 瓶有限元模型进行网格划分,网格单元类型主要为四节点壳单元(S4R),在部分弧度较大的区域使用三角形单元(S3R)过渡,共有12 669 个网格单元。HDPE 瓶顶部负载有限元模型如图3 所示。上板等效为不可变形刚体,使用八节点六面体缩减积分单元(C3D8R)划分网格;下板设定为离散刚性壳体。整个模型包括18 986 个单元和20 894 个节点。

图3 顶部负载有限元模型Fig.3 Top load finite element model
采用显示动力学计算顶部负载有限元模型。使用通用接触定义模型间的相互接触行为,设定摩擦因数为0.2。约束下板所有方向的自由度,使上板以4 mm/s的速度向下移动,并输出上板下表面的反作用力。
1.3 有限元模型的验证
计算有限元模型仿真分析与实验的误差,验证顶部负载有限元模型的准确性。实验装置由试验机(3369 型电子万能试验机,美国instron 公司)、上压板、下板、HDPE 瓶和计算机系统等组成。图4 比较了HDPE 瓶顶部负载实验与有限元分析的载荷–位移曲线。结果表明,有限元分析和实验具有较好的一致性。临界载荷Fmax的有限元分析数值与实验数值分别为635.22 N 与651.45 N,对应的位移分别为7.04 mm与7.42 mm,2 组结果的误差仅分别为2.49%和5.11%。

图4 HDPE 瓶顶部负载实验与仿真结果Fig.4 Experiment and simulation results for top load of HDPE bottle
临界载荷时,有限元模型和实验的HDPE 瓶形变如图5 所示。有限元模型和实验的形变都表现为瓶身上部的凹折,2 组结果在实验现象上同样表现出较好的一致性。数值和现象的一致性证明了HDPE 瓶有限元模型的准确性。
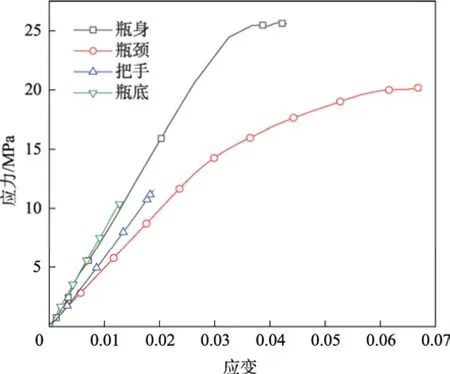
图5 HDPE 瓶顶部负载实验与有限元分析形变结果Fig.5 Experiment and simulation deformation results for top load of HDPE bottle
2 厚度对HDPE 瓶力学性能的影响
2.1 结构强度分析
瓶底的3 个区域(瓶身连接面、触地面、底面)视为一个整体。顶部负载过程中,HDPE 瓶各个部分的应力集中处的应力变化,可以表明HDPE 瓶各部分对瓶体顶部负载能力的影响。图6 为HDPE 瓶各部分应力集中处的应力–应变曲线。瓶肩与瓶底部分的厚度相近,但是瓶肩部分曲率较大,因此,瓶肩部分的刚度远小于瓶底部分;静压过程中,过大的应力导致瓶身部分的崩溃,瓶肩部分发生塑性形变几近崩溃,把手和瓶底部分始终处于弹性阶段。图7 展示了HDPE 瓶静压过程中的应力变化云图。来自上压板的压力F1经过HDPE 瓶把手传递至瓶身部分时向两边扩散,垂直方向的力与来自底板的反作用力F2平衡,两侧分力F1'作用于瓶身侧面,产生应力集中区域。因此,虽然瓶肩部分的刚度最小,但是在当前HDPE瓶厚度下,瓶身部分先于瓶肩部分崩溃。
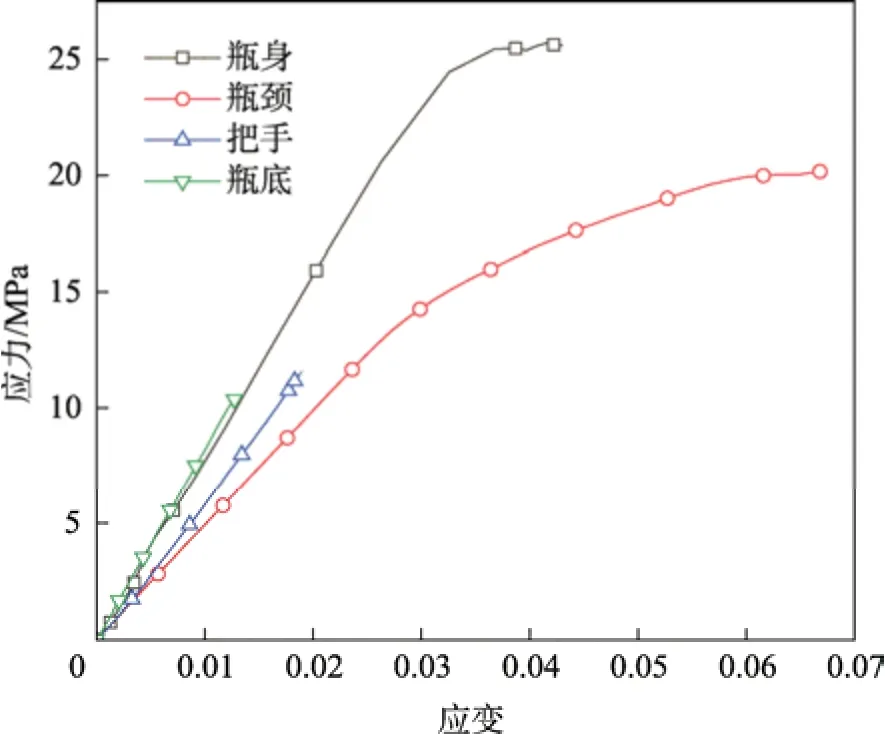
图6 HDPE 瓶各部分应力集中处应力–应变曲线Fig.6 Stress-strain curve at the stress concentration of each part of the HDPE bottle
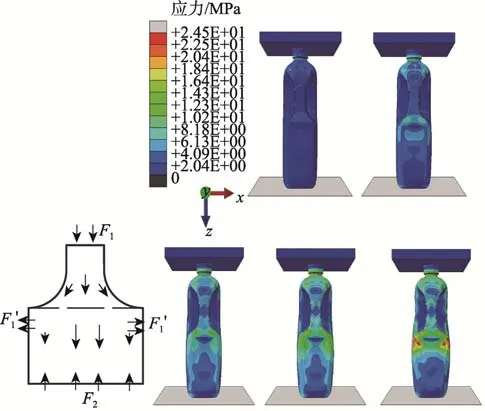
图7 HDPE 瓶顶部负载应力变化云图Fig.7 Cloud map of stress change on top load of HDPE bottle
2.2 顶部负载有限元分析
采用控制单一变量法研究HDPE 瓶各部分厚度对瓶体临界载荷的影响。有限元分析时,控制HDPE瓶某一部分的厚度改变量在0.2 mm 以内,其余部分厚度保持初始状态。不同厚度下的HDPE 瓶顶部负载临界载荷如图8 所示。单一部分的厚度增加时,顶部负载的临界载荷增大至一定数值后保持不变。这一规律表明,HDPE 瓶各个部分厚度的比值同样会影响瓶体顶部的负载能力。
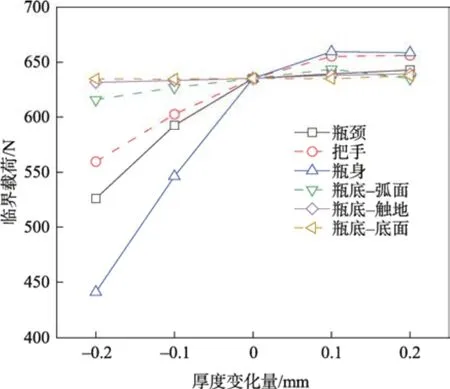
图8 不同厚度下的HDPE 瓶顶部负载临界载荷Fig.8 Critical load on top of HDPE bottle at different thickness
定义瓶肩厚度da与瓶身厚度dc的比值为厚度比η1,把手厚度db与瓶身厚度dc的比值为厚度比η2。参考HDPE 瓶初始厚度,分别改变da和dc,仿真分析η1对HDPE 瓶顶部负载的影响,结果如图9a 所示。当η1小于1.42,仅改变瓶身厚度时,顶部负载临界载荷变化趋势表明,当前厚度比下的瓶身厚度对HDPE 瓶的顶部负载能力无显著影响,HDPE 瓶顶压崩溃现象为瓶体颈部凹陷;当η1大于1.45 时,仅改变瓶肩厚度时,临界载荷停止增大,当前厚度比下的瓶肩厚度不再影响HDPE 瓶的顶部负载能力,此时,HDPE 瓶顶压崩溃的象为瓶体瓶身凹折。HDPE 瓶某一部分的厚度变化不再改变顶部负载的临界载荷时,这一部分厚度过大以致HDPE 材料浪费。因此,材料应用效率最佳时,η1的取值范围为1.42~1.45,此时,HDPE 瓶顶压崩溃应力云图如图9b 所示,现象为颈部凹陷和瓶身凹折。
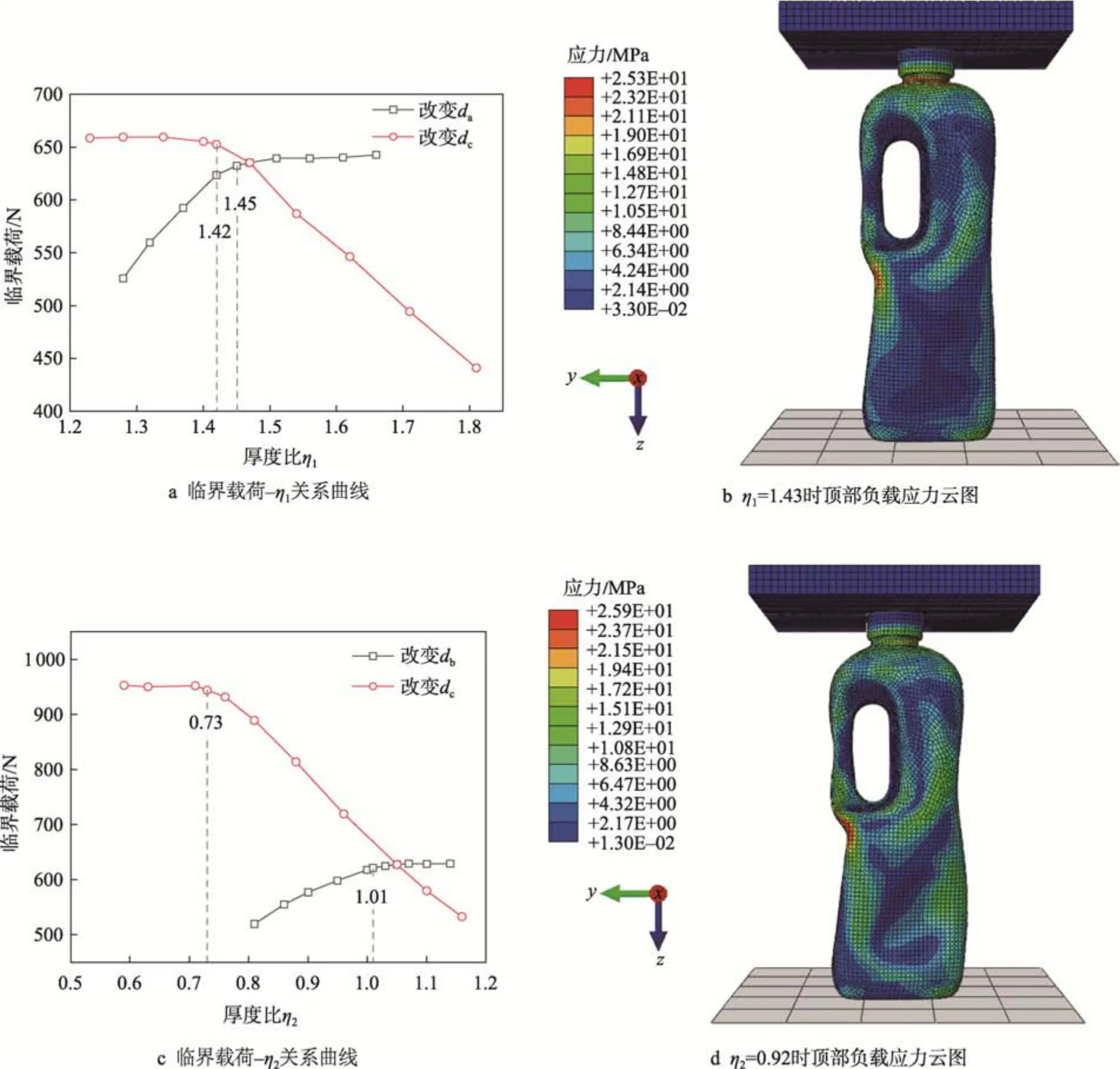
图9 临界载荷–厚度比关系曲线及仿真应力云图Fig.9 Critical load-thickness ratio curve and cloud map of simulated stress
合理的η1范围内,最佳的材料分配要求瓶肩与瓶身部分具有相同大小的临界载荷。分析临界载荷–厚度比曲线,2 条曲线分别在η1大于1.42 和η1小于1.45 时表现出线性关系,斜率k1a和k1c分别为瓶肩和瓶身厚度影响下的单位临界载荷改变量。经线性拟合得出,k1c=−553.58 N、k1a=631.86 N。根据k1a与k1c,HDPE 瓶瓶肩与瓶身部分的最佳厚度比η1=1.43。
η1=1.43 时,参考HDPE 瓶初始厚度,分别改变db与dc,仿真分析η2对HDPE 瓶顶部负载能力的影响。图9c 展示了顶部负载临界载荷与η2的关系曲线。η2大于0.73 时,瓶身的厚度对HDPE 瓶顶部负载能力产生显著影响;η2小于1.01 时,把手部分的厚度对瓶体顶部负载能力产生显著影响。拟合2 条曲线的线性部分,把手厚度影响下的单位临界载荷改变量k2b=494.01 N,瓶身厚度影响下的单位临界载荷改变量k2c=−1 006.78 N。据k2b与k2c可得,HDPE 瓶把手与瓶身部分的最佳厚度比η2=0.92。η2=0.92 时的HDPE 瓶顶压崩溃应力云图如图9d 所示。
2.3 HDPE 瓶轻量分析
通过密度法对HDPE 瓶进行轻量化分析。保持HDPE 瓶的总质量不变,瓶肩、把手和瓶身厚度处于最佳厚度比,使用ABAQUS 软件对HDPE 瓶进行拓扑优化。轻量化分析过程中,优化区域为把手和瓶身部分,最小化材料体积作为目标函数,结果如图10 所示。实际生产过程中,无法实现瓶体在较小的区域内产生多个详细定义的厚度值,因此,对拓扑优化结果进行改进设计,设计图如图11 所示。参考 GB/T 13508—2011[16]可得,白色的优化区域厚度dt=0.5 mm。
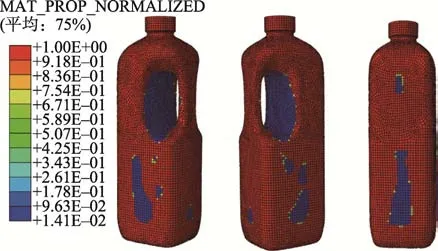
图10 拓扑优化得到的HDPE 瓶材料体积分布Fig.10 Material volume distribution of HDPE bottle obtained by topology optimization

图11 改进的HDPE 瓶壁厚分布Fig.11 Wall thickness distribution of improved HDPE bottle
分别对最佳厚度比下总质量m不变的HDPE 瓶(Design–1),以及在Design–1 基础上划分拓扑优化区域的HDPE 瓶(Design–2)进行顶部负载仿真分析,并结合2 种优化方案得到与初始HDPE 瓶(Design–0)顶部负载强度相同的HDPE 瓶(Design–3)。仿真结果见表1。
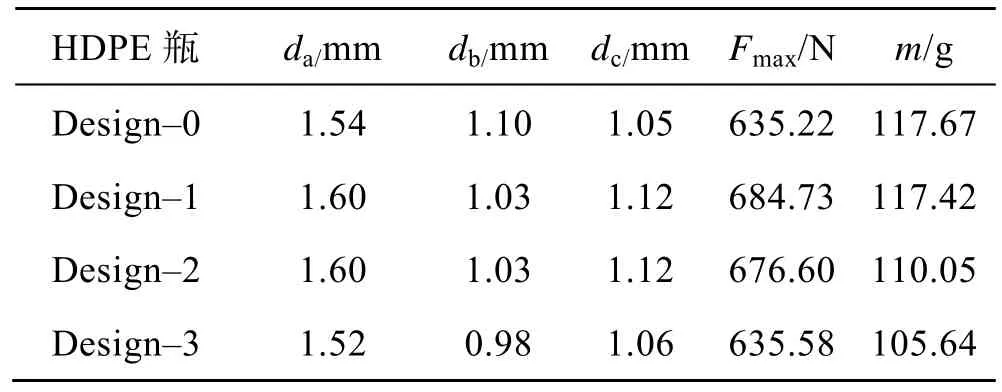
表1 各种HDPE 瓶临界载荷和质量Tab.1 Critical load and mass of various HDPE bottles
Design–1 瓶在总质量不变的前提下临界载荷增大了50 N,说明调整瓶体不同区域的厚度比可以有效改变HDPE 瓶的抗顶压能力。Design–2 瓶的临界载荷较Design–1 瓶的减少了8 N,但质量减少了7.4 g,证明了拓扑优化分析的有效性。综合2 种方案轻量化设计的Design–3 瓶在抗顶压能力不变的前提下减塑12 g。
3 结语
通过3D 扫描技术得到准确的牛奶包装HDPE 瓶外观模型,利用商业有限元软件ABAQUS 建立HDPE瓶顶部负载有限元模型,并通过静压实验验证有限元模型的准确性。分析HDPE 瓶顶部负载的过程,仿真分析瓶肩、把手和瓶身的厚度分布对HDPE 瓶顶部负载能力的影响。数值仿真的结果可以得出以下结论:
1)分段定义厚度的HDPE 瓶有限元模型可以准确预测HDPE 瓶顶部负载时的临界载荷和形变。
2)顶部负载时,瓶肩部分刚度最小,瓶底厚度对HDPE 瓶顶部负载能力无显著影响;把手结构导致瓶身部分的应力集中,瓶身部分最先崩溃。
3)设计带有把手的HDPE 瓶时,应关注HDPE瓶各部分的厚度组成,以获得更好的瓶体力学性能。

