组合参数对频变自由型垫高阻尼结构振动性能的影响

易少强，吴晓阳，赵晓明，魏 维

(武警海警学院 机电管理系，浙江 宁波 315801)

0 引 言

舰船主机、齿轮箱、轴系、螺旋桨以及其他辅助机械设备的运转所带来的振动与噪声，不仅影响舰船设备结构的稳定性与舰船的声隐蔽性，而且不利于船员正常的休息，影响工作效率。为了降低振动和噪声对舰船的危害，从而提高现代舰船的技术指标，必须对舰船进行减振降噪处理。粘弹性材料在结构振动传递的过程中有着出色的耗损机械能的能力，使共振频率降低或转移，从而达到振动级和噪声级的技术指标，因此广泛应用于各工业部门。在工程设计中,使用的粘弹性材料通常需要铺设于金属结构表面组合为复合阻尼结构,目前成熟应用的复合阻尼结构一般分为自由型阻尼结构和约束型阻尼结构，其中自由型阻尼结构早已应用在国外舰艇上，如美国、日本、印度等国舰艇的声呐舱、设备基座、浮阀等部位采用片状自由型阻尼结构[1]。为了追求更佳的减振特性，通常需要附加较厚的粘弹性材料，导致自由型阻尼结构附加质量过大，不利于改善舰船的有效载重量。随着结构轻量化设计理念的普及，对舰船减振降噪的轻量化设计提出了更高要求，如何研制兼具附加质量小、减振降噪性能优的阻尼结构就显得尤为重要。

在大量探索自由型阻尼结构减振机理的基础上，衍生出自由型垫高阻尼结构的设计思路，通过添加一层抗剪刚度极大而抗弯刚度极小的垫高层，使结构的耗能水平得到大幅度提升，同时垫高层的密度较小，也能减小附加质量的引入。Whitter等[2]从动力学的角度研究自由型垫高阻尼结构的减振机理；戴德沛[3]受自由型阻尼结构损耗因子表达式的启发，改进损耗因子的表达式，使其能表征自由型垫高阻尼结构的阻尼特性。曾海泉等[4]将垫高层的作用视为软弹簧，从而将自由型垫高阻尼结构等效为质量弹簧减振系统。陈炳等[5 – 6]构建自由型垫高阻尼结构的理论模型，并分析各结构层参数对阻尼特性的影响，后续在Ansys平台上利用PLANE183单元建立自由型垫高阻尼结构的有限元模型开展结构参数和材料参数的优化设计。易少强等[7]考虑到工程上应用自由型垫高阻尼结构采用粘结的施工工艺，构建含胶层的自由型垫高阻尼结构有限元模型，从而分析胶层参量对振动性能的影响。梁龙强等[8]制备了自由型垫高阻尼梁的样品，采用单点锤击法对悬臂自由型垫高阻尼梁进行实验，进而得到垫高层参量对结构特性的影响规律。桑英杰等[9]对自由型垫高阻尼结构进行改进，开发出开孔垫高层的复合阻尼结构，采用有限元仿真与样品试验的方式，探究孔径与复合阻尼结构阻尼性能的相关性。

粘弹性材料的复常量模型广泛应用于自由型垫高阻尼结构的数值仿真计算中，而这种简化处理忽略了粘弹性材料的频率相关性。考虑到Ansys具备可靠度较高的有限元计算功能，而Matlab具备强大的数值计算功能，同时Matlab和Ansys两者能相互调用，因此利用二者的优势对自由型垫高阻尼矩形板的几何参量、材料参量等组合参数进行仿真分析，从而探讨组合参数对频变垫高阻尼结构的振动特性的影响。

1 迭代模型的建立

自由型垫高阻尼结构的几何模型为矩形板，其结构简图如图1所示。结构参数：板长a=0.2 m，板宽b=0.1 m，基层板厚度hb=3 mm，垫高层板厚度hs=3 mm，约束层板厚度hv=3 mm。材料参数：基层板选择钢，弹性模量Eb=2.06×1011Pa，密度ρb=7 800 kg/m3，泊松比μb=0.3；垫高层板选择Dyad606材料，弹性模量Es=2.90×108Pa，密度ρs=1 200 kg/m3，泊松比μs=0.35；阻尼层板选择LD-400材料，密度ρv=1 524 kg/m3，泊松比μv=0.49,阻尼层粘弹性材料通过分数导数模型拟合其特性，表达式如下[10]：

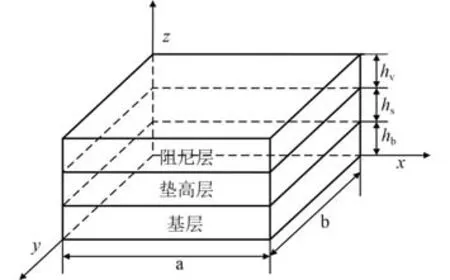
图1 自由型垫高阻尼结构示意图Fig.1 Schematic diagram of unconstrained stand-off layer damping structure

式中：E∗为粘弹性材料的复弹性模量；fr为等效频率；f为当前频率；αT为温频转换系数；T为当前温度；T0=15.6℃为参考温度。

建立悬臂自由型垫高阻尼矩形板的有限元模型时，选择具有塑性、蠕变、超弹、黏弹、黏塑和单元技术自动选择等特性的实体单元SOLID186单元，运用Ansys2022编写的APDL命令流与Matlab2022实现仿真计算数据的交互，实现迭代求解自由型垫高结构的动力学方程。仿真迭代计算的详细步骤如下：

1）定义初始温度、初始频率，对有限元模型进行仿真计算，提取模态频率；

2）将模态频率代入表征粘弹性材料特性的分数导数模型中，求得材料的初始参量；

3）更新阻尼层材料参量，进行模态分析，求解得到模态频率；

4）比较步骤1、步骤3的模态频率，如果满足收敛容差，则输出步骤3模态频率和损耗因子，否则返回步骤2，用步骤3中的模态频率更新粘弹性材料的参量，进行循环迭代，直到满足终止条件。

2 组合参数对自由型垫高阻尼结构振动特性的影响

2.1 附加层厚度的影响

垫高层、阻尼层的厚度区间选择[1,6]mm，自由型垫高阻尼矩形板的一阶模态频率和损耗因子与垫高层、阻尼层厚度的相关性为非线性关系。随着垫高层、阻尼层厚度在区间内的不断增加，引起结构整体刚度和整体质量增加，阻尼层拉伸形变的程度和粘弹性材料用量的综合效能更佳，而结构整体刚度的增益量优于整体质量的增益量。

阻尼层拉伸耗能水平逐渐增强，使系统第1阶模态频率有增大的趋势。

通过分析图2与图4曲线变化的趋势可知，第2阶模态频率的变化趋势与第1阶模态频率的变化趋势类似；通过分析图3与图5曲线变化的趋势可知，第2阶模态损耗因子的变化趋势与第1阶模态损耗因子的变化趋势类似。

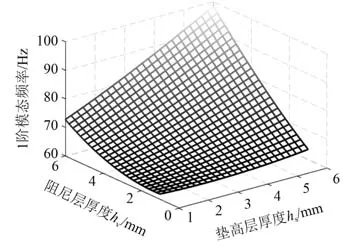
图2 附加层厚度对第1阶模态频率的影响Fig.2 Effect of additional layer thickness on first-order modal frequencies

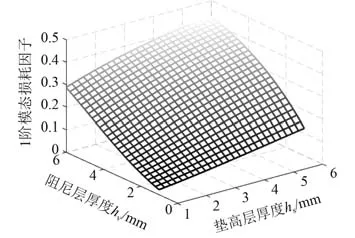
图3 附加层厚度对第1阶模态损耗因子的影响Fig.3 The effect of additional layer thickness on the first-order modal loss factor

图4 附加层厚度对第2阶模态频率的影响Fig.4 The effect of additional layer thickness on second-order mode frequencies

图5 附加层材料参量对第2阶模态损耗因子的影响Fig.5 Effect of additional layer material thickness on second-order modal loss factors

2.2 附加层材料参量的影响

垫高层弹性模量的区间选择[10,100]MPa，垫高层密度的区间选择[100,1000]kg/m3，自由型垫高阻尼矩形板的1阶模态频率与垫高层的密度相关性基本为线性关系，与垫高层弹性模量的相关性为非线性关系。当垫高层的密度不变，随着垫高层弹性模量在区间内的不断增加，引起结构整体刚度不断增加，使系统第1阶模态频率有增大的趋势；当垫高层的弹性模量不变，随着垫高层密度在区间内的不断增加，引起结构整体质量不断增加，使系统第1阶模态频率有减小的趋势。

垫高层弹性模量的区间选择[10,100]MPa，垫高层密度的区间选择[100,1000]kg/m3，自由型垫高阻尼矩形板的1阶模态损耗因子与垫高层的密度相关性基本为线性关系，与垫高层弹性模量的相关性为非线性关系。当垫高层的密度不变，随着垫高层弹性模量在区间内的不断增加，引起阻尼层拉伸形变的程度更大，使阻尼层拉伸耗能水平逐渐增强，使系统第1阶模态损耗因子有增大的趋势；当垫高层的弹性模量不变，随着垫高层密度在区间内的不断增加，引起阻尼层拉伸形变的程度几乎不变，使系统第1阶模态损耗因子基本保持不变。

通过分析图6与图8曲线变化的趋势可知，第2阶模态频率的变化趋势与第1阶模态频率的变化趋势类似；通过分析图7与图9曲线变化的趋势可知，第2阶模态损耗因子的变化趋势与第1阶模态损耗因子的变化趋势类似。

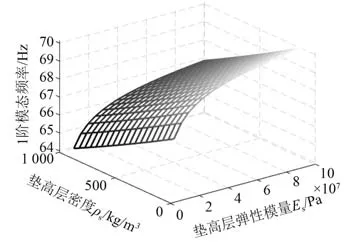
图6 附加层材料参量对第1阶模态频率的影响Fig.6 The effect of additional layer material parameters on first-order modal frequencies

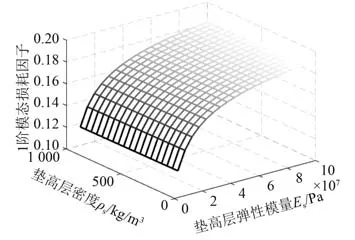
图7 附加层材料参量对第1阶模态损耗因子的影响Fig.7 The effect of additional layer material parameters on the first-order modal loss factor

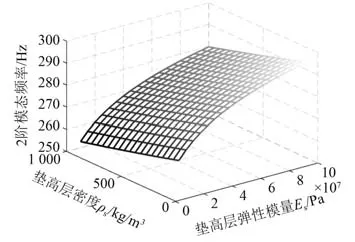
图8 附加层材料参量对第2阶模态频率的影响Fig.8 The effect of additional layer material parameters on second-order mode frequencies

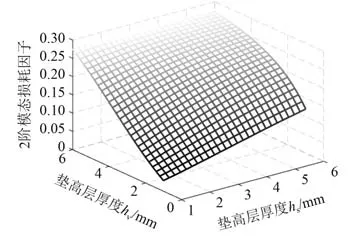
图9 附加层材料参量对第2阶模态损耗因子的影响Fig.9 Effect of additional layer material parameters on second-order modal loss factors

3 结 语

考虑粘弹性材料的频变特性，通过分数导数模型表征其材料特性，利用Ansys平台建立自由型垫高阻尼矩形板有限元模型，基于模态应变能迭代法探讨组合参数对悬臂矩形板的振动特性的影响，得到以下结论：

1）附加层结构厚度参数对系统模态损耗因子的影响主要体现在两方面：一方面垫高层对阻尼层拉伸形变的促进作用，将改善阻尼层的耗能效益；另一方面阻尼层粘弹性材料的用量，将提高阻尼层的耗能总量。因此，工程应用自由型垫高阻尼结构要充分考虑这两点的综合效能。

2）垫高层密度对模态损耗因子几乎没有影响，而垫高层弹性模量影响阻尼层的耗能水平，因此，研制大幅度提高阻尼层耗能水平，同时密度又小的垫高层材料，具有很高的工程应用价值。

3）分析组合参数的影响时，第1、第2阶模态特性具有类似的变化趋势，因此考虑系统的多阶模态特性时可以重点关注特定阶次的特性。