基于小波包和聚类算法的滚动轴承故障检测研究

杨 健，张永平

（盐城工学院 信息工程学院，江苏 盐城 224051）

随着现代工业技术的飞速发展，机器设备日益庞大复杂，机器故障特别是其中的轴承故障也日益增多，因此实时监测轴承运行状况并进行故障诊断变得越来越重要。基于无监督学习的故障诊断方法是近年来故障诊断领域的一个研究热点，Kmeans 算法是其中比较经典的算法之一，由于该算法简单、实用以及能快速收敛等特点，被运用于诸多领域。Kmeans 算法通常会随机选择k个点作为初始聚类中心，以此来确定初始划分，如果初始聚类中心的选取不合理，很容易陷入局部最优解［1］。因此，很多学者都在Kmeans 算法上作了一些改进，并取得了一系列成果。邓海等［2］将密度法与最大最小原则相结合，对Kmeans的初始聚类中心点选择进行了优化，使得算法的准确率有所提高，但时间复杂度也比较高，耗费时间较长；赵庆［3］采用Canopy 算法粗聚类数据，克服了传统Kmeans中心点随机选取的盲目性，提升了模型的精确度，但Canopy 算法的初始阈值是人工设定的，导致聚类结果不太稳定；刘纪伟等［4］用密度思想优化了Kmeans初始中心点的选取，同时引入聚类有效性判别函数确定值，提高了算法的准确度，但也增加了算法的运行时间，执行效率较低；李晓瑜等［5］用MapReduce 分布式框架并行化实现改进的Canopy-Kmeans 算法，具有很好的精确度和可扩展性，但人工设定Canopy 算法的初始阈值问题依然存在；李琪等［6］提出一种基于密度峰值的M-Canopy-Kmeans 算法，为Canopy-Kmeans算法初始中心点的随机选取、算法受噪声点影响等问题提供了解决思路；陈胜发等［7］提出基于密度加权的Canopy 改进K-medoids 算法，改善了算法的精准度；王海燕等［8］提出使用Canopy+算法用于实现对T1，T2的改进。

Canopy 算法的全局寻优性具有很好的聚类效果，可以弥补传统Kmeans算法随机选择初始聚类中心的缺陷。因此，本文在传统Kmeans算法的基础上，提出一种结合小波包分解和优化Canopy-Kmeans 算法的滚轴故障检测方法，并在西储大学滚轴数据集上进行测试，结果表明该方法可有效提高滚轴故障检测的准确性和稳定性。

1 基本理论

1.1 小波包分解

小波包分解是一种改进小波变换缺点的算法。小波变换在低频段具有较好的频率分辨率，但在高频段的频率分辨率却很差，所以信号的细节在小波变换时并不能很好地表示出来。小波包分解的基本思路是把信号分解为多个层次，即对各个频段进行分解包括分解高频部分的频段，然后根据分解后的特征选取对应的频段。图1为小波包三层分解结构图。

图1 小波包三层分解结构图Fig. 1 Structure diagram of wavelet packet three-layer decomposition

1.2 Canopy-Kmeans算法

Kmeans 算法基本思路是：在给定的数据集合中随机选择k个数据作为k个聚类的初始中心点；然后按照距离最近的原则将数据集中其余数据分配给最近的一个聚类，直到数据集是空集为止；最后，通过各个聚类的样本均值对聚类中心进行更新，直到聚类中心点没有变化或达到终止条件后再输出最终的聚类中心和k个聚类划分。

Canopy-Kmeans 算法是在Kmeans 算法的基础上加入Canopy 算法的一种优化方法，流程如图2 所示。在图2 的Canopy-Kmeans 算法中，Canopy算法首先对数据集进行“粗”聚类，然后将得到的n个Canopy 子集的中心点作为Kmeans 算法的初始中心点，再用Kmeans 算法进行“细”聚类，最终得到聚类结果。

Canopy-Kmeans 算法虽然克服了Kmeans 算法中初始中心点随机选择和人工设定的问题，但也存在如下问题：Canopy 算法的初始阈值需要经验法或交叉验证法等进行确定，使得聚类结果的稳定性下降；同时，由于时间复杂度高，导致串行运算速度慢。

1.3 I-Canopy-Kmeans聚类算法

I-Canopy-Kmeans 算法是在Canopy-Kmeans算法的基础上，对初始聚类中心的选取和阈值获取方式方面进行了优化，主要表现为：在初始聚类中心的选取方面，I-Canopy-Kmeans 算法是按照“最远最近原则”进行的，即在得到n个Canopy时，任意两个Canopy 中心点之间的距离都要尽可能地远，且第n个Canopy 中心点应该是其他数据点与前面n-1 个中心点最远距离中最小的一个；在阈值获取方式方面，主要是使用欧氏距离求出所有数据点的均值点，再计算均值点到所有数据点的距离，并用L1表示最远距离、L2表示最近距离，然后将赋值给阈值T1、赋值给阈值T2。具体地说，I-Canopy-Kmeans 算法在对初始聚类中心的选取和阈值获取方式方面进行优化的主要流程如下：

步骤1 根据给定的数据集D，计算D中所有数据间的平均距离dM。

步骤2 将平均距离dM在数据集D中对应的点称为均值点，计算均值点和所有数据之间的欧氏距离dij，并将最远的距离dij，max记为L1、最近的距离dij，min记为L2，同时将赋值给阈值T1、赋值给阈值T2。

步骤3 选取D中距离均值点最近的点c1，作为第1 个Canopy 的聚类中心，并将c1添加到中心点集合C中，即C=｛c1｝。

步骤4 计算D中所有数据与c1之间的欧氏距离dij。如果dij＜T2，就把它从数据集D中删除；如果dij＜T1，就把它分配到c1所在的Canopy 中，同时从数据集D中删除；如果dij≥T1，则比较各个dij大小，并将最大者对应的点作为第2 个Canopy 聚类中心c2，同时将该点添加到中心点集合C，使C=｛c1，c2｝。

步骤5 计算数据集D中所有数据（点c1除外）与c2之间的欧氏距离dij。如果dij＜T2，就把它从数据集D中删除；如果dij＜T1，就把它分配到c2所在的Canopy中，同时从数据集D中删除。

步骤6 在数据集D中寻找距离c1最远的点d1和距离c2最远的点d2，从中选择距离更近的点作为第3 个Canopy 聚类中心c3，并将该点添加到中心点集合C，此时C=｛c1，c2，c3｝。

步骤7 计算数据集D中所有数据（点c1、c2除外）与c3点之间欧氏距离dij。如果dij＜T2，就把它从数据集D中删除；如果dij＜T1，就把它分配到c3所在的Canopy中，同时从数据集D中删除。

步骤8 在数据集D中寻找距离c1最远的点d1、距离c2最远的点d2、距离c3最远的点d3，从中选择距离更近的点作为第4 个Canopy 聚类中心c4，并将该点添加到中心点集合C，此时C=｛c1，c2，c3，c4｝。

步骤9 计算数据集D中所有数据（点c1、c2、c3除外）与c4点之间欧氏距离dij。如果dij＜T2，就把它从数据集D中删除；如果dij＜T1，就把它分配到c4所在的Canopy中，同时从数据集D中删除。

步骤10 按照步骤8、步骤9 继续在数据集D中寻找其他聚类中心点，直到数据集D中只剩下各个中心点为止。

步骤11 将生成的Canopy 数量赋值给K，Canopy 的中心点作为聚类初始中心点进行Kmeans聚类。

上述优化流程中计算数据集中数据之间的欧氏距离如式（1）所示，计算数据集中所有数据间的平均距离如式（2）所示。

式中：dM为数据集X中所有样本元素间的平均距离，其中X＝｛x1，x2，…，xn｝是一个包含n个样本对象的数据集，每个样本对象包含d维特征属性；dij为数据集X中数据对象xi和xj之间的欧氏距离；xip（i＝1，2，…，n；p=1，2，…，d）表示第i个数据对象的第p维属性，xjp（j＝1，2，…，n；p=1，2，…，d）表示第j个数据对象的第p维属性。

2 I-Canopy-Kmeans 聚类算法的故障检测方法

I-Canopy-Kmeans 聚类算法的滚轴故障检测流程如图3 所示，主要包括基于小波包分解的数据预处理、特征向量归一化和I-Canopy-Kmeans算法的故障检测模型训练3个方面。在具体的滚轴故障检测中，先用三层小波包分解滚轴数据，求出滚动轴承特征向量；将特征向量归一化以获得新的样本集，并将样本集划分为训练集和测试集；使用I-Canopy-Kmeans 算法对训练集中的数据进行训练，建立滚轴故障检测模型后，再将测试集中的数据引入到滚轴故障检测模型中，对模型进行有效性检验。

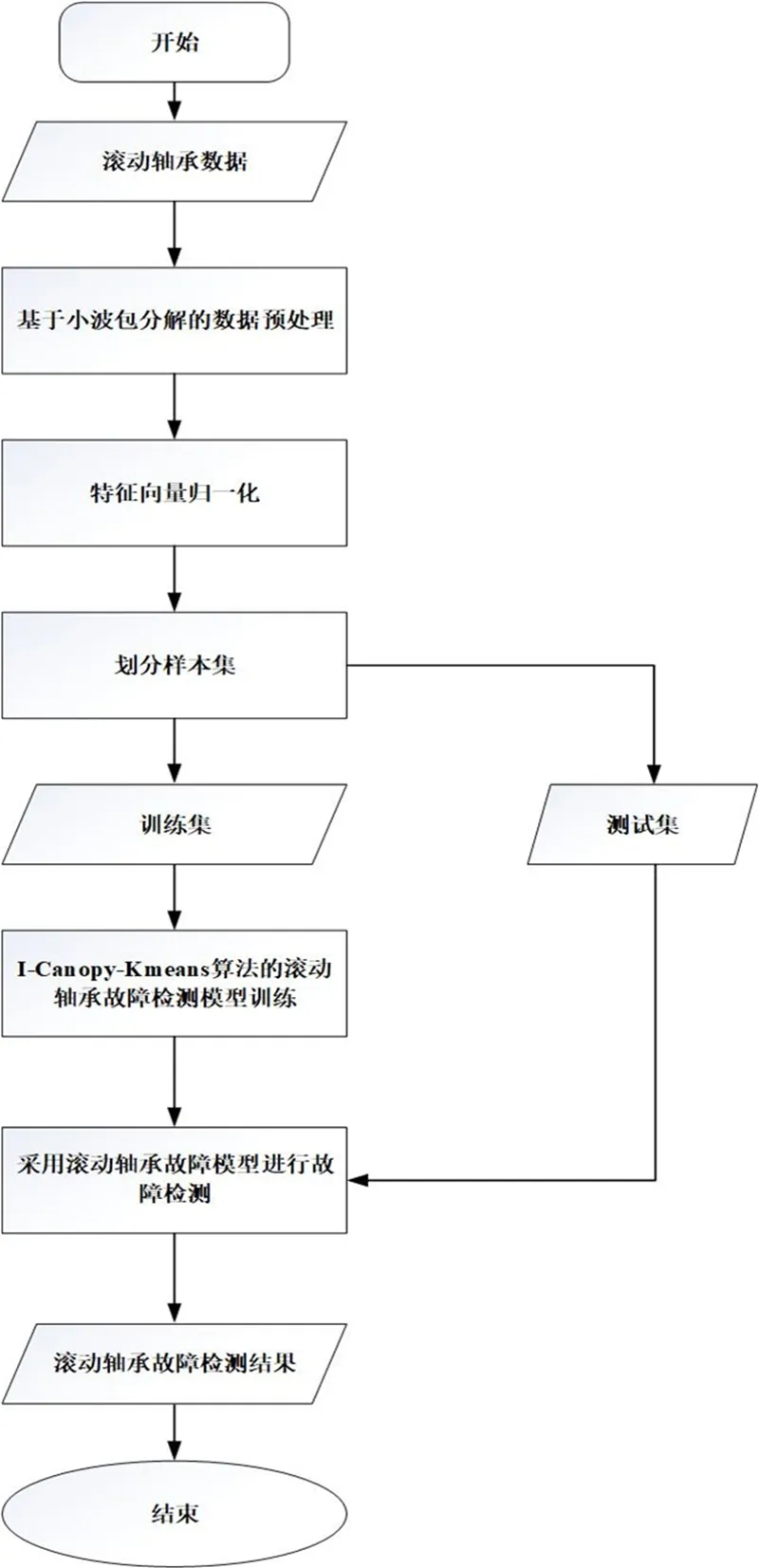
图3 滚轴故障检测流程Fig. 3 Flow of roller fault detection

2.1 基于小波包分解的数据预处理

一般来说，滚轴通常有4种运行状态，分别为正常状态、外圈故障、内圈故障和滚动体故障。由于滚轴振动信号不同频段的能量分布代表滚轴不同的运行状态［9-10］，本文采用三层小波包分解对滚轴振动信号进行分析，得到8个小波包的分解频段，再通过计算得到各频段的能量及能量所占比例，进而根据能量分布构建滚轴不同运行状态的特征向量。

按照帕塞瓦尔（Parseval）定律，信号时间内的总能量等于其频率范围内的总能量。小波包分解仅改变了信号的形态，将信号的高频成分与低频成分分开，分解前后的总能量保持不变。若对信号x（t）进行小波包分解，得到n层频带信号，则各子频带信号的能量计算如式（3）所示。

式中：Enm表示第n层第m个频段的能量，J；Sa，b表示二维系数矩阵，其中a是尺度参数，b是位移参数；xn，m(k)表示第n层第m个频段中第k个小波包的系数值；x（t）为原始信号，t为时间变量，s。

总能量E为：

如以每个子频段的能量百分比表示该信号的特征向量，则信号的特征向量T可以表示为：

通过小波包分解，获得了多个特征向量，该特征向量包括8 个频段的能量，这些特征向量将取代原有的庞大振动数据集，作为新的数据集来使用。

2.2 特征向量归一化

为提高检测模型的训练速度，需要将小波包分解后得到的特征向量T按式（6）进行归一化处理。

式中：xm′(m= 1，2，…，8)是特征向量中第m个频段归一化后的结果；xm是特征向量中第m个频段的能量值；xmax、xmin分别是特征向量中的最大值与最小值。

3 实验过程及结果分析

3.1 振动数据特征提取

基于美国凯斯西储大学提供的滚动轴承数据集［11］，采用I-Canopy-Kmeans 聚类算法的滚轴故障检测方法，对滚轴振动数据使用三层小波包分解并进行特征提取，得到不同状态下不同频段的能量百分比，如图4 所示。其中特征提取的部分数据如表1所示。

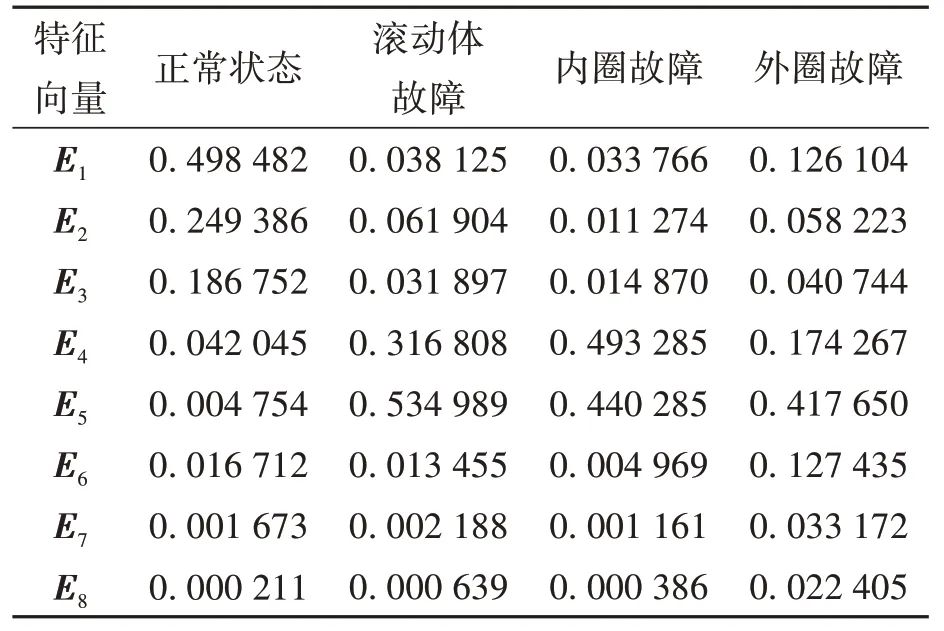
表1 特征提取的部分数据Table 1 Partial data of feature extraction

图4 滚轴不同状态下的能量谱Fig. 4 Energy spectrum of the rollers in different states

由图4 可以看出，不同状态下信号的能量分布是有差异的，其中正常状态下的滚轴能量主要分布在第1、2 频段，故障状态下的能量主要分布在第4、5 频段，且滚动体及外圈故障的能量分布在第4、5 频段更加集中，滚轴内圈故障的能量分布则稍微分散于1、2、3、6 频段；在滚动体及外圈故障中，外圈故障在第6个频段的能量分布比前3个频段更多，而滚动体故障在前3 个频段的能量分布比第6个频段更多。

3.2 实验过程及结果分析

基于表1 的特征提取数据，采用传统的Kmeans 算法和I-Canopy-Kmeans 算法分别计算两种算法下各自经历1 000 次实验的滚轴平均故障检测准确率，结果如表2 所示。由表2 可知，采用传统Kmeans 算法得到的聚类效果评价指标中标准化互信息INM为0.709 3、调整互信息IAM为0.705 7、兰德系数IR为0.849 1、调整兰德系数IAR为0.553 8，采用I-Canopy-Kmeans 得到的INM为0.782 8、IAM为0.781 3、IR为0.9093、IAR为0.775 4。显然，采用I-Canopy-Kmeans 检测算法的各项指标得到明显提高，其中，IAR提高最多，从0.553 8提高到0.775 4，提高了40.01%。

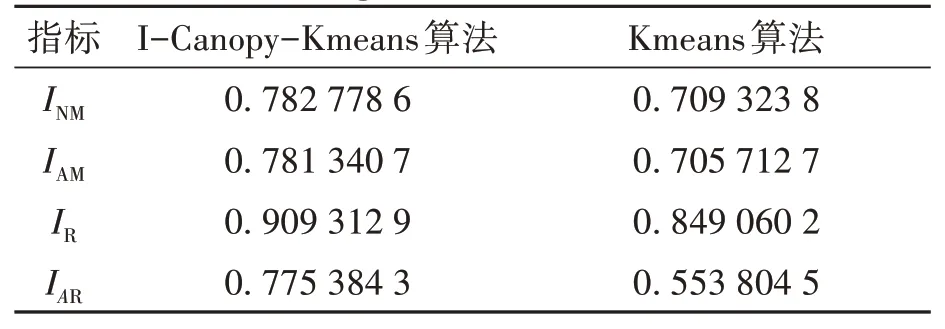
表2 算法评价指标Table 2 Algorithm evaluation metrics

经过比较分析，发现两种算法下得到的聚类中心对应的特征向量均有变化，分别如表3、表4所示。表3、表4 说明传统的Kmeans 算法可能得到了局部最优解，I-Canopy-Kmeans 算法则更可能得到了全局最优解。

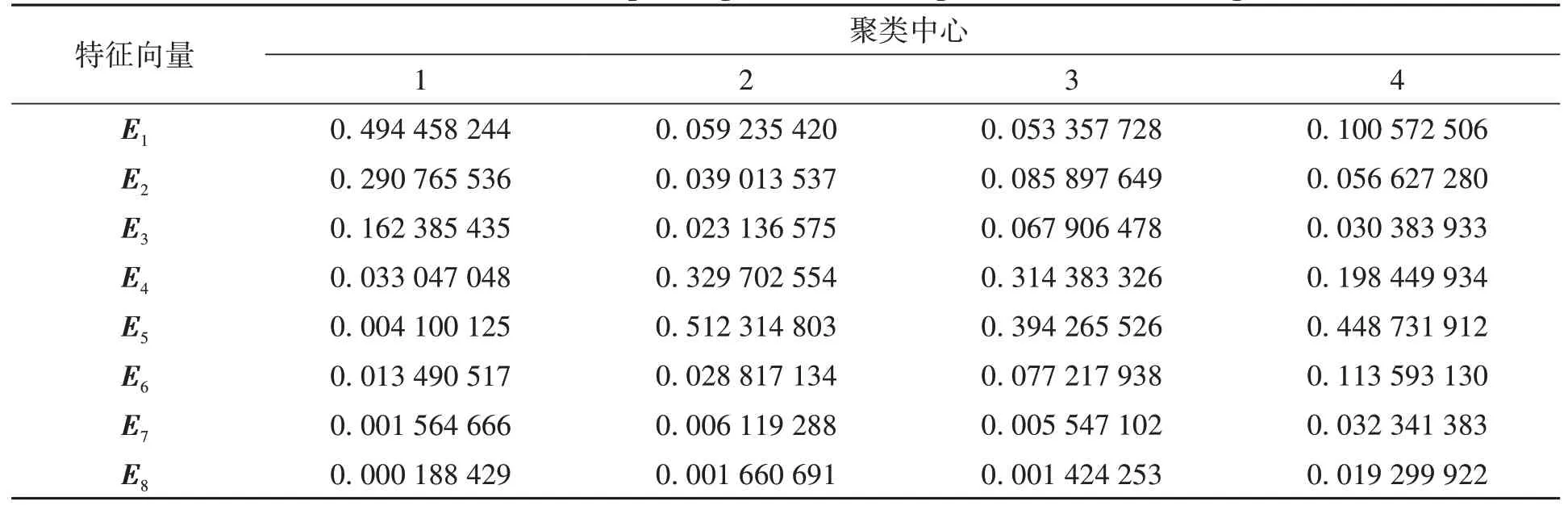
表3 使用Kmeans得到的聚类中心对应的特征向量Table 3 Feature vectors corresponding to the clustering centers obtained using Kmeans

表4 使用I-Canopy-Kmeans得到的聚类中心对应的特征向量Table 4 Eigenvectors corresponding to clustering centers obtained using I-Canopy-Kmeans

4 结束语

I-Canopy-Kmeans 算法在Canopy-Kmeans 算法的基础上，改进了初始聚类中心的选取问题，优化了阈值的选取方式。实验结果表明，与传统的Kmeans 算法相比，I-Canopy-Kmeans 算法的各项评价指标均有提高，其中指标IAR提高最多，提高了40.01%。