考虑库存与中断的双目标多式联运优化研究

王能民， 王雪宁， 史玮璇

（1.西安交通大学 管理学院，陕西 西安 710049；2.陕西省制造服务业过程挖掘工程研究中心，陕西 西安 710049）

1 引言

随着互联网的普及、国家政策的支持以及疫情的传播，方便、无接触的跨境电商［1］得到高速发展。据海关统计数据，2021年我国跨境电商进出口1.98万亿元，增长15%［2］。顾客满意度是决定电商持续发展的重要因素［3］，海外仓通过物流前置极大地缩短顾客的收货时间，进而提升其购物体验，同时海外仓还可以减少因为道路中断等风险因素对供应链的冲击。目前，中国海外仓的数量超过2000个，面积超过1600万平方米［4］。对跨境电商企业而言，同时考虑海外仓管理以及多式联运路径规划是一个复杂系统工程问题，如何在降低成本与提升顾客满意度两个目标下对其进行高效的求解具有重要的实际应用价值。

与本研究相关的研究成果主要包括两部分：考虑中断风险的多式联运的研究，以及考虑库存的多式联运的研究。关于考虑中断的多式联运类的成果以最小化成本的单目标研究为主，部分研究采用加权法将风险、时间或碳排放等多目标转化为单目标求解。Wagenaar等［5］考虑中断风险以及顾客的满意度，以最小化成本为目标，设计启发式算法进行求解。Ke［6］考虑到火车某些节点出现中断的情形，以风险和成本为双目标，采用鲁棒优化模型将成本目标转化为约束条件，将风险作为单一目标进行优化。考虑多式联运在长距离运输大批货物的优势，Demir等［7］以其为研究对象，以运输成本、违反时间窗成本与CO2排放为优化目标，通过加权法转化为单一目标进行求解，采用随机优化的方式将运输时间与需求的不确定性考虑到模型中。

关于考虑库存的多式联运优化的研究，主要以最小化成本的单目标为主：贺竹磬等［8］，魏航等［9］虽然在最小化物流费用的目标函数中包含了库存成本，但只是货物在规定的时间点前送达而产生的积压库存，是对违反时间窗的一种惩罚，而不是对库存的决策优化。Marufuzzaman和Eksioglu［10］在以生物质能转化为燃料来供应城市为背景的研究中，以最小化成本为单目标，由于生物质能产生的季节性，会在转化工厂进行存储，并将存储量作为决策变量进行优化。

综上本文解决的是考虑库存管理和道路中断的双目标多式联运优化的系统工程问题，主要创新点包括：（1）问题方面，首次考虑海外仓对跨境电商决策的影响，将多式联运、订单分配以及道路中断风险等因素联合优化。（2）模型方面，以最小化总成本与最大化顾客满意度为双目标，建立了两阶段的优化模型，第一阶段采用鲁棒优化法考虑道路中断对路径选择的影响，将决策结果作为第二阶段的参数，对订单的满足方式与时间进行决策，并据此更新库存水平。（3）算法方面，针对中小规模算例设计精确算法，基于问题特点在ε-约束法的基础上进行改进：通过性质求ε的下界，规避不可行路径以及利用改进的标号法求解子问题，得到帕累托前沿；针对大规模算例在ε-约束法的基础上设计了贪婪随机自适应搜索与模拟退火的混合启发式算法。（4）管理启示方面，发现海外仓的存在可以极大地降低成本与顾客的等待时间，而安全库存量与补货量则需要结合海外仓实际的需求量进行合理的制定，在库存成本与运输成本之间进行平衡。

2 问题描述与建模

2.1 问题描述

G（V，E，M）代表多式联运的无向交通网络［11］，其中V＝｛0，1，．．．，n｝为节点集合，E＝｛（i，j）｜i，j∈V｝为边集。M为运输方式的集合，每条弧上都有至少一种运输方式，同一条弧上不同运输方式的时间与成本不同，且遵循时间越短成本越高的基本规律［12］，当不同的运输方式之间进行转换的时候会产生转运成本与时间，为了突出重点，本文不考虑运量不匹配的问题，假设转运成本与时间为常量［10］。I⊂V为海外仓的节点集，跨境电商需对海外仓的库存进行管理。跨境电商处理订单的周期为TD，期初得到该期顾客订单集合R，每个订单信息包括需求量Qr、起点Or、终点Dr、产生时间Er以及最晚送达时间Lr。企业根据当期订单需求与库存量决策订单的满足方式，当顾客需求大于库存量时，一部分订单采用库存方式满足，根据订单的最晚送达时间要求，决策由当期还是下期库存进行满足；一部分订单采用直邮方式满足，需对直邮订单进行路径规划。该阶段的决策变量直接影响库存，当库存低于安全库存点时补货。顾客满意度与需等待的时间直接相关。S为道路中断的情景集合，不同情景会改变交通网络，本文采用鲁棒优化的最坏情况分析法［13］，以对结果影响最大的中断情景作为基准。以总成本最小和顾客满意度最大为双目标，求解跨境电商如何选择运输的方式与路径以及如何安排订单的满足方式。

本文假设包括：（1）不考虑订单的分割与合并；（2）订单只在每期期初产生；（3）不考虑最后一公里问题；（4）每周期只了解当期需求，无法预知未来；（5）不考虑仓库之间的补货；（6）不考虑运力不匹配的情况。

2.2 数学模型

2.2.1 符号说明

集合。V为节点集合，E为边集，M为运输方式的集合，T为时间集合。

参数。wr为订单r得到满足需要等待的时间。为 每单位FTU的产品从i点到j点以m方式运输的成本。为每单位FTU产品在i点从m运输方式转化为¯m的成本。为每单位FTU的产品从i点到j点以m方式运输的时间。为每单位FTU产品在i点从m运输方式转化为¯m的时间。为情景s下，从i到j采用m方式运输的路段是否中断，若中断其值为0，否则为1。Ii为仓库i的初始库存。INit为仓库i在t时的库存。Qit为仓库i在t时运达的货物数量。Qi为仓库i的补货量。Hi为仓库i储存一个FEU集装箱所载产品的单位时间库存成本。Ai为仓库i的安全库存量，低于此值的时候，发出补货请求。Ci为每个FEU集装箱产品从起点到仓库i的补货运输成本。LTi为每个FEU集装箱产品从起点到仓库i的补货运输时间。Bit为仓库i在t时是否进行补货。CZr为订单r采用直邮方式运输时决策者偏好方案的运输与转运成本。TZr为订单r采用直邮方式运输时决策者偏好方案的等待时间。

yrim ¯m，0-1变量，1表示订单r在i点从运输方式m转化为¯m，否则为0。Zr，0-1变量，1表示用订单r由海外仓库存满足，0表示用直邮方式满足。Tr，表示订单r由库存满足的时刻，决策由当期或是下期库存满足。

2.2.2 第一阶段

针对每个订单在保证不违背其时间窗以及考虑各种道路中断的情景的前提下，对其运输路径以及运输方式进行决策，模型如下

目标（1）最小化在对结果影响最大的中断情景下每个订单由直邮产生的运输与转运费用，目标（2）最小化在对结果影响最大的中断情景下每个订单由直邮运输所需的平均等待时间，（3）每个中断情景下的直邮的运输与转运费用，（4）每个中断情景下直邮订单等待的时间，（5）节点i与j之间只能采用一种方式进行运输，（6）节点i最多只能转运一次，（7）表示运输服务的连续性，（8）保证节点间流量守恒，（9）保证处于中断状态的路径不可以通行，（10）和（11）表示不能违背订单的时间窗约束，（12）和（13）为决策变量的取值范围。

2.2.3 第二阶段

据第一阶段计算得出的每个订单采用直邮的帕累托前沿，决策者从中选择一个偏好方案作为第二阶段的参数，之后需要针对每个订单是否采用库存进行满足以及满足的时间进行决策，并根据决策结果对库存水平进行更新，模型如下

目标（14）最小化总成本，包括海外仓产生的库存成本，补货的运输成本以及直邮成本，目标（15）最小化总时间，包括海外仓满足的订单所需的等待时间，以及直邮的运输时间，（16）初始化每个海外仓的库存，（17）每个周期根据是否有补货到达以及订单需求量来更新库存水平，（18）保证海外仓的库存水平不为负值，（19）根据库存水平判断是否下达补货请求，（20）在补货请求下达一个提前期的时间以后货物到达海外仓，（21）海外仓满足的订单不能超过每个订单规定的时间窗，（22）和（23）规定了决策变量的取值范围。

3 模型分析与求解

本文涉及不同的交通方式间转换的成本与时间，将现实的点按其拥有的交通方式转化为几个虚拟点［14］，转运时间和成本转化为虚拟点间路径的时间与成本，这样第一阶段的子问题可以转化为有时间约束的最短路问题，属于资源约束的最短路问题，是NP-hard问题［15］。因此本文求解的问题也是NP-hard问题。

3.1 基于ε-约束法的精确算法

第一阶段按不同的中断情景拆分，分别计算不同情景对目标函数的影响，本文的鲁棒优化采用最坏情况分析法，最后以对结果影响最大的中断情景为基准。那么原问题可以转化为多个双目标整数规划问题P。针对多目标问题，加权法因操作简便得到了最广泛的应用，但此方法无法得到完整的帕累托前沿。因此ε-约束法［16］被提出，其思想为将除一个目标以外的其他所有目标转化为约束条件，将多目标问题转化为多个单目标问题。本文基于ε-约束法将多目标问题P转化为多个单目标问题P0。其中ε的取值范围表示为）和。此后根据本文问题特点，在经典ε-约束基础上做出三处改进。

问题P

s.t.约束（3）～（13）

问题P0

3.1.1 确定ε的取值范围

对于ε-约束法，首先需要确定ε的取值范围，令εU与εL分别代表ε的上下界，其中，其中可通过求解问题P2得到，同理可以通过求解问题P1得到。

问题P1

s.t.约束（3）～（13）

问题P2

s.t.约束（3）～（13）

经典的ε-约束法需求解混合整数规划模型问题P1和问题P2。本文通过分析问题结构的特殊性得到如下性质，可以用一个时间复杂度为O（nlogn）的迪杰斯特拉算法［17］计算得到fI2。

性质问题P2是以时间为权重的最短路问题。

证明每条弧有（时间，成本）两个数据，只取弧上的时间作为权重，求解起点到终点的最短路径，即为问题P2的解。

3.1.2 确定不可行路径集合

因为ε-约束法每次迭代不同的问题P0时，其约束中的ε一直在减小，每次迭代生成的解x*的路径总是会因为ε约束的收紧而减少，而被淘汰的路径在后续的迭代过程中一定是不满足更加严格的ε约束的，因此可以在计算之前就将这些路径划分在不可行路径集合中，从而在后续的迭代过程中缩小搜索范围，减少算法运行时间。向不可行路径集合中添加不可行路径的算法如下。

算法1A第1步 对于当前解x*的路径集合P*，将所有路径按照运输时间降序排列，从集合P*中按顺序依次取出路径，记为pi。第2步 如果T（pi）＞ε，将pi放入不可行路径集合Pinf中，返回上一步，否则终止算法。

3.1.3 改进的标号法

在解决带资源约束的最短路问题的精确算法中，基于动态规划的标号法占主导地位［18］。但传统的标号法没有对不可行路径的判断，需在原算法的基础上改进，具体步骤如算法1B所示。

1B输入：路径网络数据，订单的时间约束、初始点Or和终点Dr，以及不可行路径集合P算法inf初始化：集合U←（Or），P←Ø当U≠Ø时一直进行如下循环：（路径扩展）选择一条路径Q∈U并将其从集合U中移除：对于以点vQ为起始点的所有的弧（vQ，w）∈A：如果路径（Q，w）不属于Pinf也不违反订单的时间约束，并且w不在路径Q中：将路径（Q，w）添加到集合U中P←P∪｛Q｝（支配检验）对于集合U∪P中的路径应用支配规则从集合P中识别出总成本最小的路径并输出输出：最短路径

综上，在传统ε-约束法的基础上做出三处改进后的整体求解思路如算法1所示。

算法1第1步 确定对结果影响最大的中断情景，并以此为基准进行计算第2步 利用迪杰斯特拉算法求解问题P2，利用算法1B求解问题P1，得到ε的取值范围第3步 用算法1A更新不可行路径集合Pinf第4步 用算法1B求解问题P0，得到时间与成本的最优解向量x*，将x*加入到解列表Y′第5步 令ε＝f2（x*）-1，如果ε≥f I2，回到第3步，否则，转到下一步第6步 将Y′中的被支配解删除，得到帕累托前沿Y，决策者针对每个订单选择一个偏好解第7步 将偏好解代入第一阶段模型，计算得到最优解

3．2 基于ε-约束法的启发式算法

由于带资源约束的最短路问题是NP-hard问题，对于大规模算例，上述的精确算法无法求解，因此基于上文的ε-约束算法设计了一个贪婪随机自适应搜索（GRASP）与模拟退火（SA）的混合启发式算法，求解算法2的问题P0与问题P1。GRASP与SA 被广泛应用于调度以及车辆路径等问题［19，20］。GRASP有构造初始解和局部搜索两部分，其中局部搜索部分融合SA进行优化，根据本文问题特点分别对两部分进行设计。

3.2.1 生成初始解

在算法2A中，第6步的参数α∈［0，1］用来控制算法贪婪与随机的比重，当α＝0时，只选取最优的候选元素，是纯贪心算法；当α＝1时，所有候选元素都可以随机选择，是纯随机算法。

算法2A输入：起点o，终点d，参数α，时间矩阵，距离矩阵，时间约束第1步 初始解s为由起点与终点组成的路径第2步 初始化候选元素的集合E（指初始解中没有的元素）第3步 对候选集合中的元素e∈E进行评估。计算将元素e插入路径s中所导致的目标函数的最优改变量c（e），c（e）≥0代表加入e使得成本增加，反之代表使得成本减少第4步 当存在e使得c（e）＜0时，执行5至8步，否则返回s并结束算法第5步 令c min＝min｛c（e）｜c（e）＜0，e∈E｝，c max＝max｛c（e）｜c（e）＜0，e∈E｝第6步 选取满足c（e）≤c min＋α（c max-c min）的元素e加入限制候选列表RCL中第7步 从RCL中随机选取一个元素e，判断将其加入s是否会违反时间约束，如果不违反则s←s∪｛e｝，并更新候选集合E，否则重新选择e第8步 对候选集合中的每个元素e重新计算c（e ）

3.2.2 局部搜索

本文采用交换操作中的2＿opt算子，即反转指定区间内的元素顺序，作为邻域动作。借鉴模拟退火算法的思想设计局部搜索算法，si为当前路径，si＋1为使用2＿opt算子后的路径，T为系统温度，Tmin为温度下界，f1（s）为路径s的总成本，f2（s）为路径s的总时间，TC为时间约束，r控制降温的速度，具体如算法2B所示。

2B输入：初始路径s0，T，T min，TC，r，时间矩阵，算法距离矩阵初始化：当前路径si←s0，最优解s*←s0第1步 判断T＞T min是否满足，若满足转至第2步，否则结束算法，返回路径s*第2步 对si应用2＿opt算子得到si＋1，令Δ＝f（si）-f（si＋1）第3步 若f2（s）≤TC，转至第4步，否则返回第2步第4步 当Δ≥0时，令si←si＋1，转至第6步，否则转至第5步第5步 在［0，1］间随机生成数β，若e Δ T ＞β，令si←si＋1，转至第6步第6步 判断f（si）＜f（s*），若满足则更新最优解s*←si，转至第7步第7步 降温，令T←r×T，转至第1步

综上，混合启发式算法的整体思路如下。

2C输入：距离矩阵，时间矩阵，最大迭代次数M，起点o，终点d，算法时间约束初始化：解s←Ø，最优解s*←Ø，迭代次数k＝0第1步 判断当前迭代次数k≤M，若满足转至第2步，否则结束算法，返回最优解s*第2步 更新迭代次数k←k＋1，用算法2A生成初始可行解，并赋值给s第3步 用算法2B对s进行邻域搜索，得到一个最优解s第4步 判断f1（s）＜f1（s*），若满足更新最优解s*←s，转至第1步

将算法2C与ε-约束法结合，得到的整体算法2框架如下。

算法2第1步 确定对结果影响最大的中断情景，并以此为基准进行计算第2步 利用迪杰斯特拉算法求解问题P2，利用算法2C求解问题P1，得到ε的取值范围第3步 用算法2C求解问题P0，得到时间与成本的最优解向量x*，将x*加入到解列表Y′第4步 令ε＝f2（x*）-1，如果ε≥f I2，回到第3步，否则，转到下一步第5步 将Y′中的被支配解删除，得到帕累托前沿Y，决策者针对每个订单选择一个偏好解第6步 将偏好解代入第一阶段模型，计算得到最优解

4 算例分析

4.1 随机算例

本文借助慕尼黑工业大学研发的在线带资源约束的最短路问题工具包，随机生成不同规模算例，分别为6个小规模算例（1～6），4个中规模算例（7～10），6个大规模算例（11～16）。随机生成8个周期的订单数据，其需求量符合高斯分布。通过Python 3.8.5和Gurobi（Version 9.5.0）编程求解，所有测试均在一台个人电脑上进行（1.80 GHz CPU，16.0 GB，Windows 11）。

4.1.1 精确算法效果分析

用精确算法1计算1～10并将计算时间与用Gurobi求解的传统ε-约束法进行对比，每个算例运行5次，取均值作为最终结果，如表1所示。

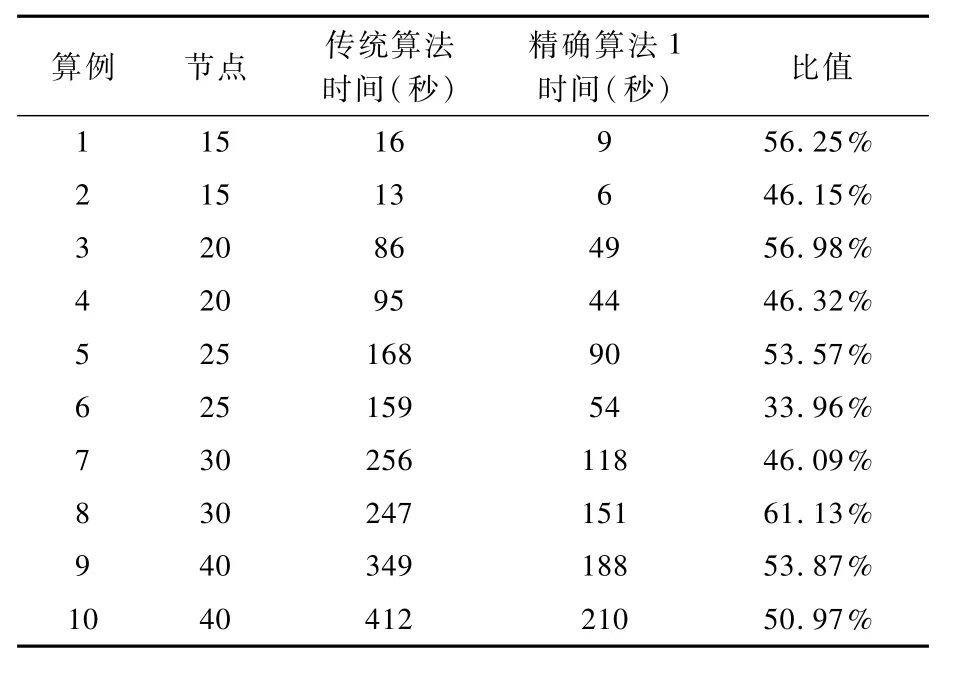
表1 传统算法与精确算法1的计算时间

在所有算例中，精确算法1的计算时间均小于传统算法，平均为传统算法的50.52%，其中表现最好的为算例6，仅为传统算法计算时间的33.96%。因此本文提出的精确算法可以有效地加速求解进程。

4.1.2 启发式算法效果分析

用启发式算法2对算例7～16进行计算，与传统算法、精确算法1和NSGA-II进行对比。其中算法2中的参数参考文献［21，22］设定为：α＝0.75，T＝f1（s0），Tmin＝0.01，r＝0.9。选定计算时间，解的数量，与最优解的平均偏离以及超体积作为衡量算法效果的指标。其中超体积指标通过计算非支配解集与参照点围成的目标空间中区域的体积［16］，来评估给定前沿的收敛性与多样性，其值越高代表解的质量越好。参考相关文献［23］，本文选择采用前文确定的作为参照点。

如表2所示，本文的启发式算法计算速度远远快于精确算法，并且精确算法无法得到大规模算例的结果；而至于计算结果，启发式算法与精确算法的成本与时间的平均偏离分别为2.15%与1.34%，超体积偏离大约在0.05～0.23之间。如表3所示，在大规模算例中，为了检验本文启发式的计算效果，我们将其与经典算法NSGA-Ⅱ的结果进行对比，可以发现在保证相同的计算时间的前提下，本文启发式算法的效果更优。

表2 传统算法与精确算法1同启发式算法2的计算效果对比

表3 启发式算法2与NSGA-Ⅱ效果对比

4.2 现实算例

4.2.1 数据说明

以南京为起点，以欧洲的不莱梅、斯武比采、巴黎与罗马为终点。节点间的距离以谷歌地图数据为基准，速度以及运费参数参照文献进行设定［24］，FEU集装箱公路运输速度按照平均值55km／h，运输费用国内以9元／箱公里，欧盟以16元／箱公里计算，铁路运输速度按照35km／h，运输费用分为独联体区段、国内段以及欧盟段，分别按照不同的价格进行计算。水运为便于计算，运输时间统一按照28天，运输费用按照26000元／箱进行计算。库存成本为每天308元／箱。不同运输方式之间转运时间与价格：公路与铁路为1h，110元／箱；公路与飞机为2h，180元／箱；铁路与飞机为3h，220元／箱。以14天为一个周期，共计算8个周期。海外仓的补货方式采用水运。所有库存以及运输单位均以FEU箱为单位，每个海外仓初始库存均为30箱，安全库存点为15箱，每次补货量为20箱。所有订单数据随机产生，其中需求量符合高斯分布。

4.2.2 现实算例分析

用传统算法与精确算法1同启发式算法2进行求解，每个算例计算5次，结果取均值。如表4，启发式算法的计算速度远大于精确算法，但是精确算法的计算效果要优于启发式算法。例如启发式算法的目标函数f1与f2平均偏离分别为2.6%与2.1%，超体积偏离在0.09～0.26之间。

表4 计算效果对比

4.2.3 不同中断情景对结果的影响

计算几个连接亚欧的长途路径中断对最优解的影响，发现只有苏州华沙铁路，杭州—列日空运，杭州—华沙公路的中断会产生影响，因此只展示这三种中断与无中断时的最优解对比。以不莱梅为终点，结果如图1所示。其中代表杭州—华沙中断的黑线之所以在无中断的红线之下，是因为黑线得出的结果数量较少导致的，而不是占优于红线。顾客的满意度随着成本的增大而提升，针对每个订单，决策者有多种选择可以达到不同水平的顾客满意度，因此需在成本和顾客满意度之间权衡。从图1可以看出，苏州—华沙的铁路中断对结果影响最大。因此本文的鲁棒优化的最差情景为苏州-华沙的铁路中断。

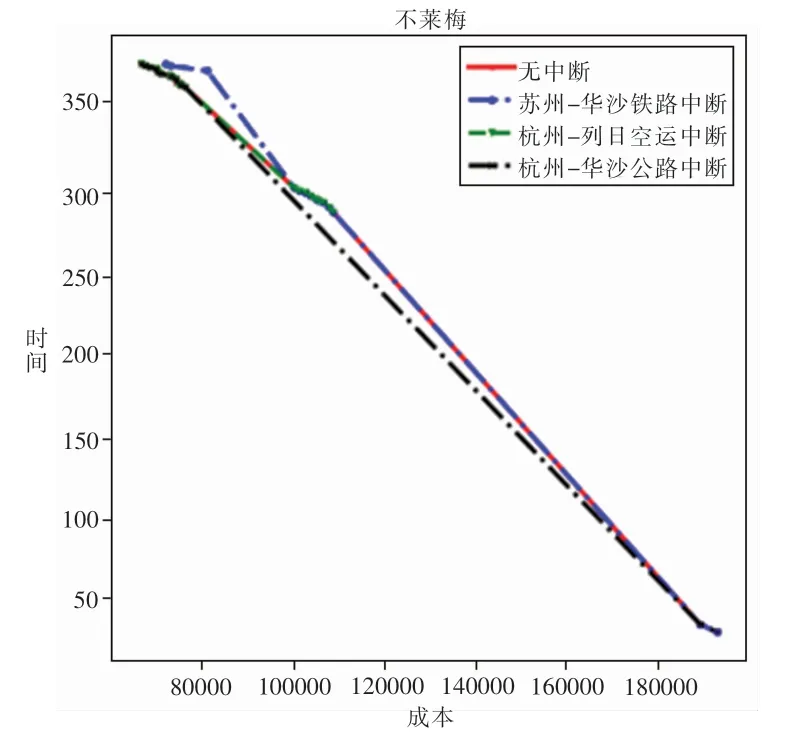
图1 不同中断情景的影响

4.2.4 模型鲁棒性检验

对比鲁棒模型与原模型得出的帕累托前沿路径方案在不同的中断情景下的表现效果。无中断情景下，原模型的表现效果更优，但一旦中断，原模型的结果波动明显，相比之下，鲁棒模型在多种不同的中断情景中，结果的平稳性大大优于原模型。深入分析原因我们发现，鲁棒模型的路径搭配更加多样，但是原模型的路径方案大部分都选用单一路段，因此抗风险性大大降低。由此可知，本文的鲁棒模型路径方案可以有效应对道路中断风险。

4.3 灵敏度分析

4.3.1 有无海外仓的结果对比

以不莱梅为终点，结果如图2所示。由图2可知，海外仓可以大幅度减少时间与成本。因为与直邮多花费的运输成本相比，因海外仓存在而增加的库存成本是很小的。这也解释了海外仓近几年越来越多的社会现象。

图2 有无海外仓的影响

4.3.2 安全库存量不同的结果对比

由图3可知，巴黎、罗马与不莱梅三个海外仓的安全库存量越高越好，而斯武比采安全库存量值越小越好。因为前三者的需求量大，当安全库存量较低时不能及时补货，部分订单需直邮，虽安全库存量值较高会增加库存成本，但与增加的直邮的运输费用与时间相比是微不足道的。而对于斯武比采而言，该地的需求量较少，因此增加安全库存量，只会导致库存的增加，安全库存量值在一定程度上减少是有利的。综上对于需求量较小的产品，应适当降低安全库存量，通过减少补货次数，降低货物积压从而降低成本。而对于需求量较大的产品，则需适当地提高安全库存量，通过增加补货次数来减少直邮，从而降低成本与等待时间。

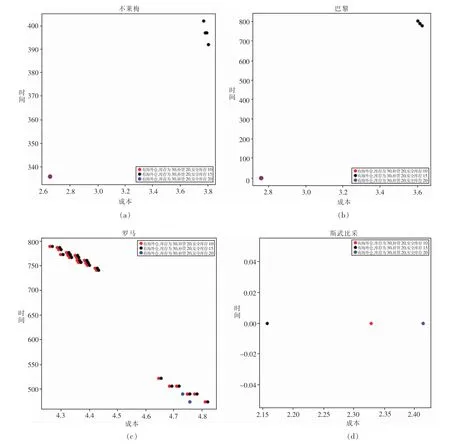
图3 安全库存点对结果的影响

4.3.3 补货量不同的结果对比

对于巴黎、罗马与不莱梅，补货量20好于30好于10，而斯武比采则是补货量10好于30好于20。因为前三者的需求量大，因此补货10单位不足以满足需求，需花费更多的成本与时间直邮，因此其结果最差；补货20可减少大部分直邮从而减少等待时间与成本；而当增加补货量为30时，虽可以进一步消除直邮，但无法抵消由此造成的库存成本的增加，导致总成本上升。而斯武比采的需求量较小，因此增加补货只会增加其库存从而增加成本，虽本文结果是补货量30好于20，但分析发现是由研究时间较短所致，若从长期的眼光来看，补货量20好于30。综上，对于需求较少的产品，需一定程度上降低补货量。而对于需求量较大的产品，需在一定范围内提高补货量，但要把握好补货的度，过高的补货量同样会导致产品积压，从而增加总成本。

5 结论与启示

本文基于跨境电商海外仓的背景，以最小化总成本与最大化顾客满意度为目标，考虑海外仓、中断以及多式联运，对其进行两阶段优化建模。针对小规模算例设计了精确算法；对于大规模算例设计了GRASP-SA的混合启发式算法。

首先用随机算例测试模型与算法，对于中小规模算例，将本文精确算法1与传统算法进行对比，证明本文算法可以加快求解速度。对于大规模算例，将启发式算法与NSGA-Ⅱ进行对比，验证启发式算法的可行性与可靠性。之后基于现实数据，运用本文精确算法与启发式算法求解，通过灵敏度分析发现：海外仓可以极大降低成本与等待时间，而安全库存量与补货量则需结合实际需求量合理地制定，对于需求较少的应适当降低安全库存量以及补货量，通过减少库存来降低总成本，而对于需求较大的产品，应适度增加安全库存与补货量，通过减少运输成本来降低总成本。

本文的不足为没有考虑未来需求，会导致决策的短视性，也因为信息的不足无法对库存补货量进行直接的优化决策。随着信息时代的到来，企业越来越重视大数据的应用［25］，未来研究可以利用机器学习预测需求来进一步对库存进行优化以提升优化效果。此外，本文没有考虑订单的合并、海外仓间的补货以及转运时的运力不匹配等问题，可以在未来补充研究。最后，可以针对这类问题开发更高效的算法。