叶片厚度分布对两级离心泵空化性能的影响

李 乐，陈二云，李国平，杨爱玲，徐 磊

（1.上海理工大学 能源与动力工程学院/上海市动力工程多相流动与传热重点实验室，上海 200093；2.上海船舶设备研究所，上海 200031）

空化在流体机械中是一种常见的不可避免的现象，空化过程中空泡的产生与溃灭会引起畸变流，并在离心泵内诱发严重的压力脉动，由此产生振动、噪声和一系列的结构性破坏［1-4］。产生这种破坏的原因之一是流体激励力，内部交替的压力场又是产生流体激励力的根源。单相流动时泵内压力场受叶轮旋转的影响发生周期性变化，空化工况下泵内压力场较为复杂，变化无明显规律。由空化诱导的压力脉动以及流体激励力会改变叶轮的受力状态［5-6］。叶片几何参数的改变能够有效改善叶轮进口的流动状态，并对空化的初生产生重要影响。因此，现对第一级叶轮叶片的厚度分布进行优化，研究其对泵外特性、非定常压力脉动以及流体激励力的影响，为降低离心泵空化损伤以及振动噪声的研究提供参考。

国内外学者针对现有离心泵叶轮存在的空化现象，分别从叶片进口角度、叶片最大厚度点、叶片进口边位置和叶片角的分布规律四个方面优化叶片［7-12］，这些研究方法应成为今后空化研究的发展方向。由前人的研究成果可知，离心泵叶轮进口的流动状态是影响空化性能的重要因素。叶轮叶片的几何参数又能对进口的流动均匀性产生重大的影响。前人通过控制叶片最大厚度点的位置来研究叶片厚度分布对离心泵空化性能的影响。值得注意的是，最大厚度点的位置在叶片上不是连续的，因此也就不能反映出泵的空化性能与叶片厚度分布规律之间的关系。

以往学者的研究对象大多集中在单级离心泵上，并考虑空化影响的情况，或者是在没有考虑空化影响条件下对两级离心泵进行研究［13-15］。因此，本文提出在考虑空化条件下，研究叶片厚度分布对两级离心泵的影响。对叶片厚度分布的研究中沿用了原始叶片对称厚度分布的规律，并采用从前缘到尾缘厚度线性过渡的方法。

1 数值计算方法

1.1 计算模型

在泵的流体计算中，一般认为水为不可压缩流体，不考虑流动过程中的能量传递过程，并且空化计算时假设温度恒定，即在整个流动过程中由于摩擦做功而产生的温度变化一般不予考虑。因此，通常在计算中只考虑质量守恒方程和动量守恒方程，而忽略能量守恒方程［16］。

（1）质量守恒方程

式中，u、v、w分别为速度矢量在x、y、z三个方向上的投影。

（2）动量守恒方程

对不可压缩流体，忽略重力，且不考虑外部体积力时，动量守恒方程可以表达为

（3）湍流模型

本文采用应用最为普遍的RNGk-ε模型，该模型对湍流黏度进行了修正，能够较好地对涡流及流动分离现象进行预测，且在分析三维旋转流体机械的流动现象时具有很好的效果［17-20］。

（4）空化模型

本文数值计算时采用全空化模型，并利用两相湍流的相互迭代，得出液相和空泡相的收敛解［21］。

1.2 参数及网格划分

整个离心泵的计算域包括：进出口延长段、第一级叶轮、正导叶、反导叶、过渡段、第二级叶轮、蜗壳。两级离心泵计算域模型如图1所示。两级离心泵结构比较复杂，因此需要对几何模型进行简化。计算域模型中忽略了正反导叶多处倒角和叶顶间隙，且不考虑转轴和全部进、出口处的密封部件。为了准确指定进、出口边界条件，分别在进、出口法兰前、后各取4倍管径的长度。为了提高计算准确度及收敛特性，采用六面体网格，并在靠近壁面处使网格自适应几何体壁面的微小变化。该泵的设计流量Q0=100m3·h-1，设计扬程H=30m ，转速n=2900r·min-1。两级离心泵各部件主要几何参数如表1所示。

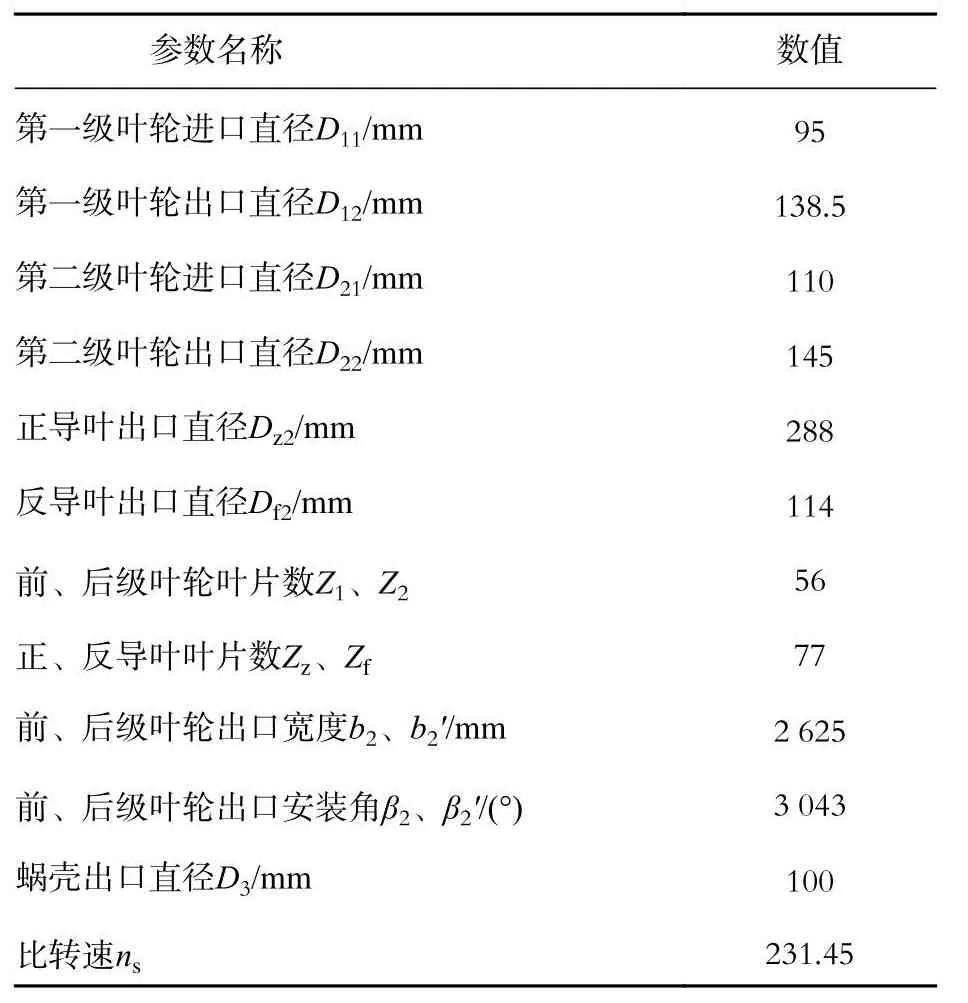
表1 两级离心泵各部件主要几何参数Tab.1 Main geometry size of each component in a double-stage centrifugal pump

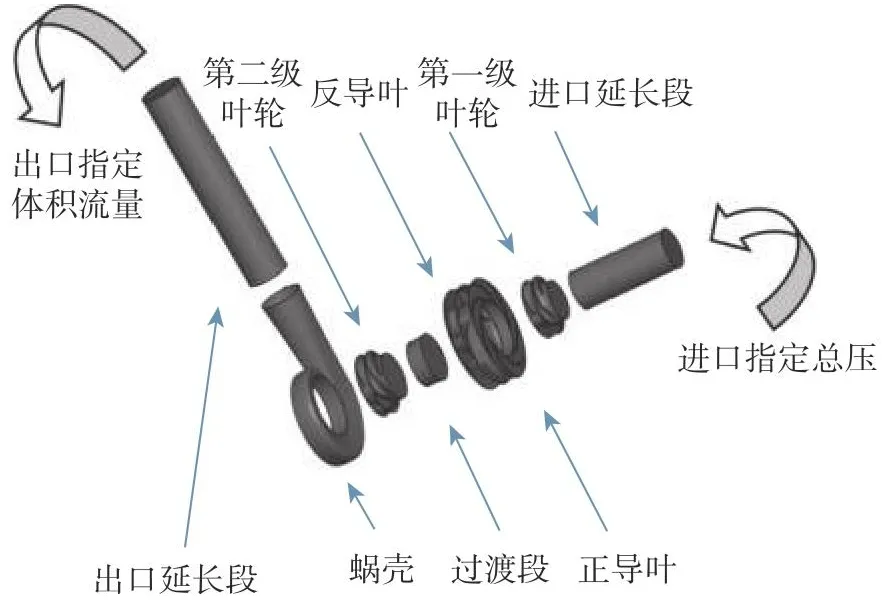
图1 两级离心泵计算域模型Fig.1 Calculation domain model of a double-stage centrifugal pump

1.3 计算方法以及边界条件

两级离心泵固壁采用无滑移、绝热边界条件，近壁面区域均使用标准壁面函数进行处理。在旋转叶轮和静止蜗壳的动静交界面采用滑移网格技术进行信息传递。

另外，来流工质包含的气体有掺混气体、水蒸气和溶解气体，为气液两相流。工质的物理参数取水温为300 K时的值，其饱和蒸汽压力pv=3 610 Pa，体积弹性模量E=2 150 MPa，蒸汽密度ρg=0.0245kg·m-3。

求解器数值差分格式采用二阶迎风格式，时间精度采用二阶精度，压力速度耦合采用SIMPLEC算法。对于收敛方案，设置最大迭代次数为200，收敛残差为10-5。

2 计算结果分析

2.1 叶片厚度分布

离心泵叶片大多采用空间扭曲形式，由于其工作面和背面均为空间曲面，叶片厚度的精确定义难以给出。为了便于理解和应用，常常用局部平面代替曲面，并引入多种叶片厚度定义方法。利用方格网保角变换绘型时，一般在轴面投影图上按照轴面截线进行加厚，以原始截线为骨线向两侧加厚，也有人利用原始骨线中的压力面或吸力面向另外一侧加厚。叶轮内流面和叶片存在交面，将此交面用锥面代替并展开成平面，此时叶片工作面和背面之间的距离为流面厚度。流面上叶片沿圆周方向的长度为圆周厚度。轴面投影图中，叶片沿流线方向的切线长度为叶片的轴面厚度。由于叶片是扭曲的，流面和叶片并不垂直，因此流面截取叶片所得的流面厚度和垂直叶片时所截得的真实厚度并不相等。

计算所用模型泵的第一级叶轮叶片为对称厚度分布，主要长度参数、主要角度参数分别如表2、3所示，叶片厚度分布如图2所示，a、b、c、d、e分别为5个控制点的相对位置，a1～e1为各点以中心线为轴的对称位置。

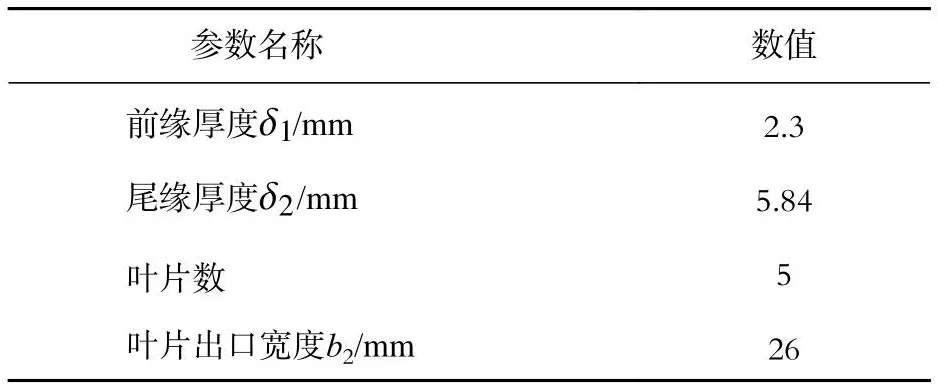
表2 模型泵第一级叶轮叶片主要长度参数Tab.2 Main length size of the first stage impeller blade of model pump

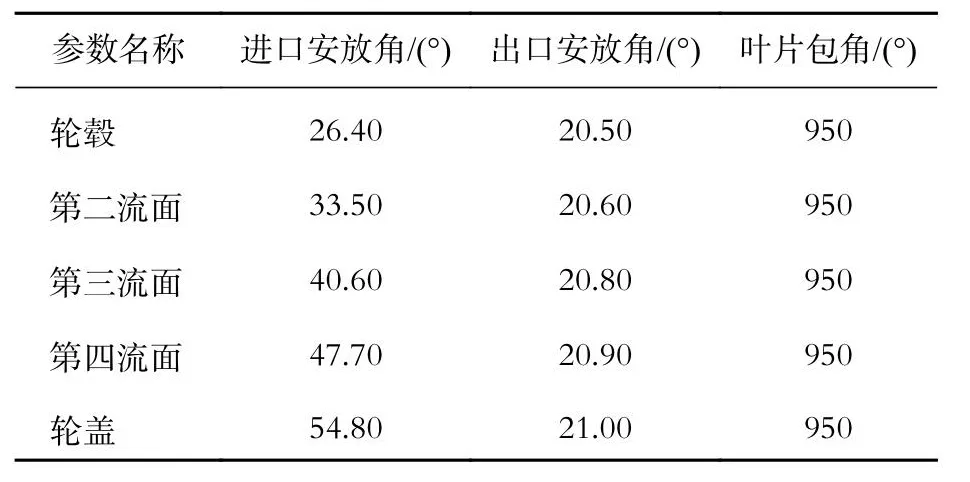
表3 模型泵第一级叶轮叶片主要角度参数Tab. 3 Main angles of the first stage impeller blade of model pump

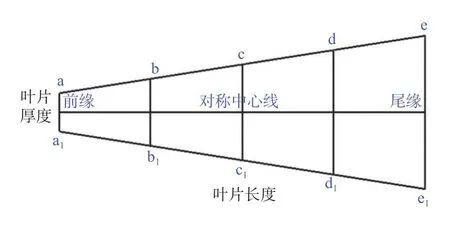
图2 叶片厚度分布Fig.2 Thickness distribution of the blade

为了研究在一定变化规律下叶片厚度分布对叶轮内部流场的影响，只改变前缘和尾缘厚度，保持叶片厚度对称分布且从前缘到尾缘呈线性变化。据此，确定了9种叶片厚度优化方案，如表4所示。

表4 叶片厚度优化方案Tab.4 Optimization of blade thickness

2.2 空化性能

图3（a）给出了两级离心泵第一级在不同方案下的空化性能曲线，其中NPSH为有效汽蚀余量。在设计工况下9种方案的空化性能曲线差异较大，表明此时叶片厚度对离心泵第一级空化性能影响较大。由图中可知：根据临界空化点的不同，9种方案大致可以分为A、B、C三组，方案1～3为A组，方案4～6为B组，方案7～9为C组。为了较为清晰地观察各种方案中的空化性能曲线在临界空化点附近的变化趋势，作局部放大图，如图3（b）。由此可见，A、B、C三组中A组曲线浮于最上方，B、C组曲线在达到临界状态之前变化趋势基本相同，但在达到临界状态之后出现了较大的差异，B组扬程下降缓慢，C组扬程下降剧烈，且C组曲线在有效汽蚀余量低于5 m后急剧下降。在工程上认为，当扬程下降3%左右时发生空化，即此时的有效空化余量为临界空化余量。可见，C组的临界空化余量最低，明显低于A、B两组。A、B两组中，A组临界空化余量最大，并且在任意工况下扬程曲线均明显高于B组。综上所述，A组方案中叶片空化性能最好。对比各组方案中叶片前缘和尾缘厚度可以发现，每组叶片前缘厚度均相同，其中A组叶片前缘厚度为三组中最小。这表明在空化流动中叶片前缘厚度对空化性能的影响较大，远远大于叶片尾缘厚度对空化性能的影响。

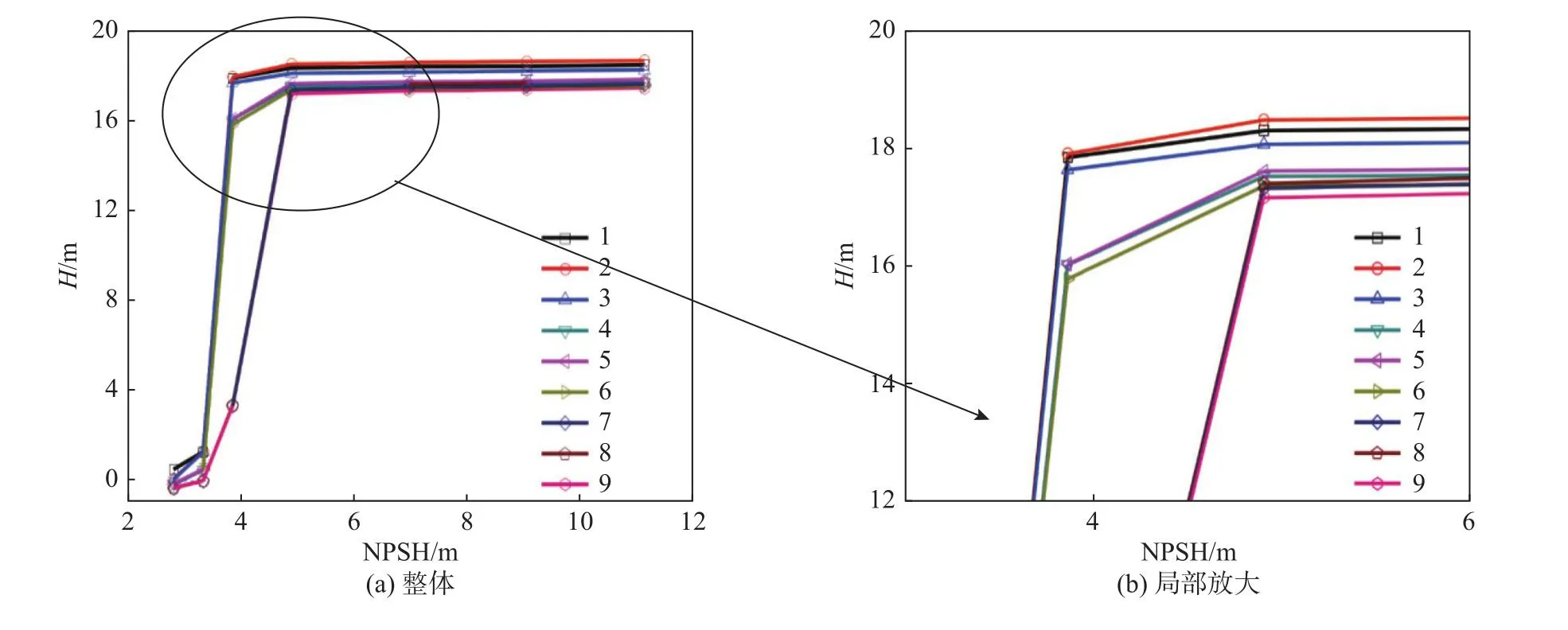
图3 两级离心泵第一级在不同方案下的空化性能曲线Fig.3 Cavitation performance curves of the first stage in the double-stage centrifugal pump in different schemes

在局部放大图3（b）中，C组的三种方案的空化性能曲线相差不大，B组各方案的临界空化余量有所差异但是相差不大，即可认为这两组方案中叶片的空化性能整体较差，可以不予考虑。A组的三种方案中临界空化余量分别为4.29、4.40、4.27 m，即方案2的空化性能最好，扬程受空化作用的影响最小，方案1次之，方案3最差。对比各方案叶片前缘和尾缘厚度发现，方案2中叶片尾缘厚度最小，方案1次之，方案3最小。这表明在具有相同叶片前缘厚度的情况下，叶片尾缘厚度越小，抗空化能力越强。

离心泵经过叶片做功后，其叶片尾缘一般处于高压区，不易发生空化；而叶片前缘靠近进口，多处于低压区，且受到运行工况等因素的影响，属于空化高发区。空化的发生会严重影响泵的性能，因此叶片前缘厚度对泵空化性能的影响较大。叶片的厚度主要影响叶轮流道的流通面积，因此当叶片较薄时，较少发生堵塞，泵的空化性能也会越好。除了考虑水力性能外，还要考虑叶片的受力情况。在叶片设计时，通过对水力性能和强度性能的综合分析，合理选择叶片的厚度，以达到经济性和稳定性的双重目标。

2.3 压力脉动结果分析

为了得到叶轮叶片厚度的改变对内部非定常流场品质的影响，在第一级叶轮某一流道的中截面位置处布置5个压力监测点，监测点1～5在叶轮流道内沿半径减小的方向布置，如图4所示。

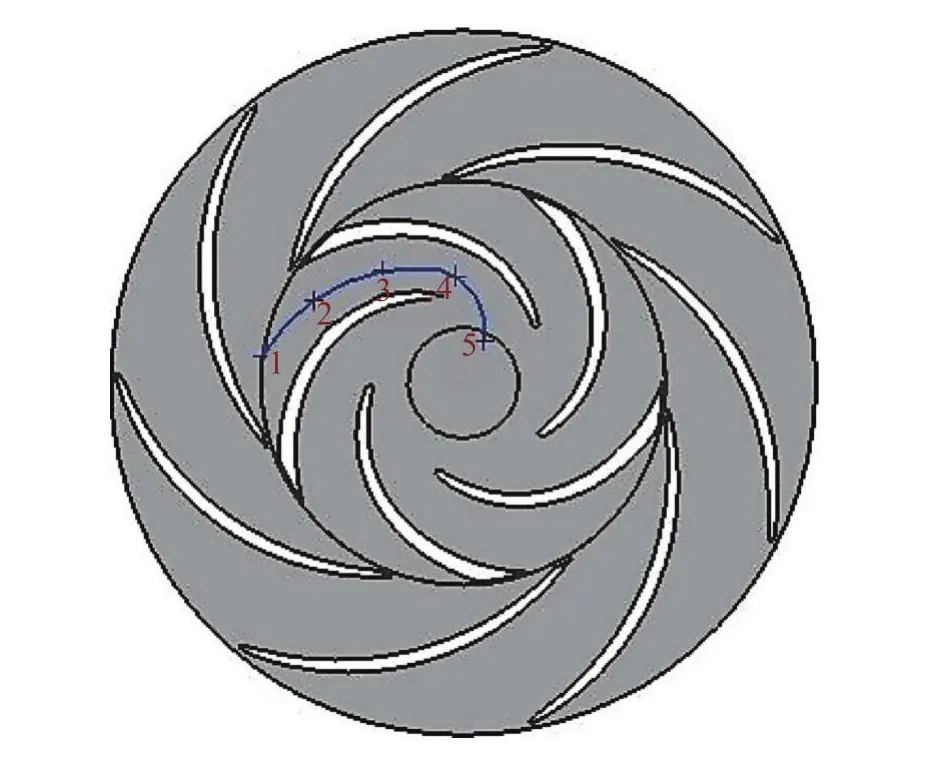
图4 第一级叶轮流道截面压力监测点分布Fig.4 Arrangement of pressure monitoring points in the cross section of the first stage impeller passage

在叶轮出口和导叶入口的狭小间隙内，沿圆周方向从导叶进口背面开始到导叶进口工作面为止设置5个压力监测点，如图5所示。在设计流量下计算10个周期后，发现压力可满足周期性要求，从而获得压力随时间的变化规律。取流动稳定后7个周期的数据进行压力脉动分析，通过快速傅里叶变换得到三种方案的压力脉动频域信号，结果如图6所示，其中：f为频率；Δp为压力脉动幅值。

图5 导叶入口压力监测点布置示意图Fig.5 Layout of pressure monitoring points at the inlet of guide vane

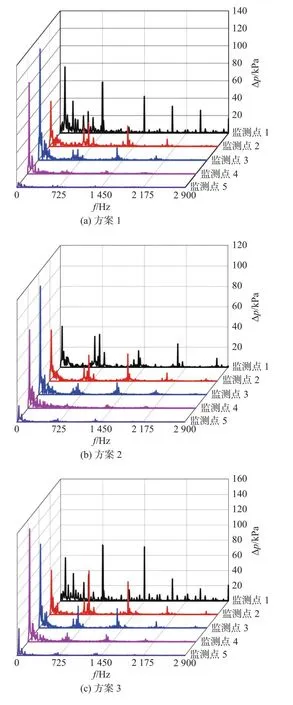
图6 不同方案中的压力脉动频谱图Fig.6 Pressure fluctuation spectra of different schemes

第一级叶轮叶片通过频率为725 Hz。由图6可知，压力脉动具有明显的离散特征，脉动峰值主要集中在低频、叶频及叶频倍频。低频压力脉动是空化的伴生现象，一般并不随着空化的加剧而增大，且在低频处还表现出高幅宽频特征。叶轮内的压力脉动主要是由叶轮旋转产生，因此脉动主频应由叶片通过频率决定。

各方案中压力脉动主要成分均为叶频及其倍频脉动，并且随着频率的增大脉动幅值逐渐降低。根据监测点1～5的数据可知：各方案中的压力脉动峰值在叶频及其倍频下均随着半径的增加逐渐增大。这主要是由于叶轮出口正对导叶，受旋转叶轮中流体射流和尾迹影响显著，动静干涉作用强烈。但是在低频区，监测点3、4的压力脉动峰值较大，并且此为各方案中的共性。这主要是由于监测点3、4位于流道喉部附近，受空化作用的影响剧烈。对比三种方案，方案3的压力脉动幅值最大，并且监测点4的压力脉动幅值已超过监测点3，可知：当叶片前缘厚度一定时，尾缘厚度越薄，叶片整体厚度越小，流道越开阔，受空化作用的影响越小；尾缘越厚，低压区前移，由于空化气体的聚集，使得喉部区域“前移”。方案2中的整体压力脉动幅值较小，由流动诱导的噪声和振动均比其他方案的低得多，因此方案2最优，核对叶片厚度后可知该方案中叶片最薄。

图7为导叶入口监测点的压力脉动情况，可见各监测点的值具有很强的一致性。导叶入口处经过叶轮做功，压力较高，因此空化初生相对较弱。但是该处可能是气泡破裂、消失的地方，仍然存在高幅宽频的低频信号，低频脉动的幅值并不随监测点的位置改变而发生较大改变，这也恰恰说明了高幅、低频的脉动现象正是空化的伴生，并不随着空化的强弱而变化。叶频信号和2倍叶频信号是整个压力脉动的主要成分，但是其主导地位与监测点位置有关。靠近导叶进口背面的监测点压力脉动幅值较大，靠近导叶进口工作面的监测点压力脉动幅值次之，流道中间位置监测点压力脉动幅值相对最小。对比三种方案可知，方案2中整体压力脉动幅值最小，对应的叶轮叶片尾缘厚度最小。

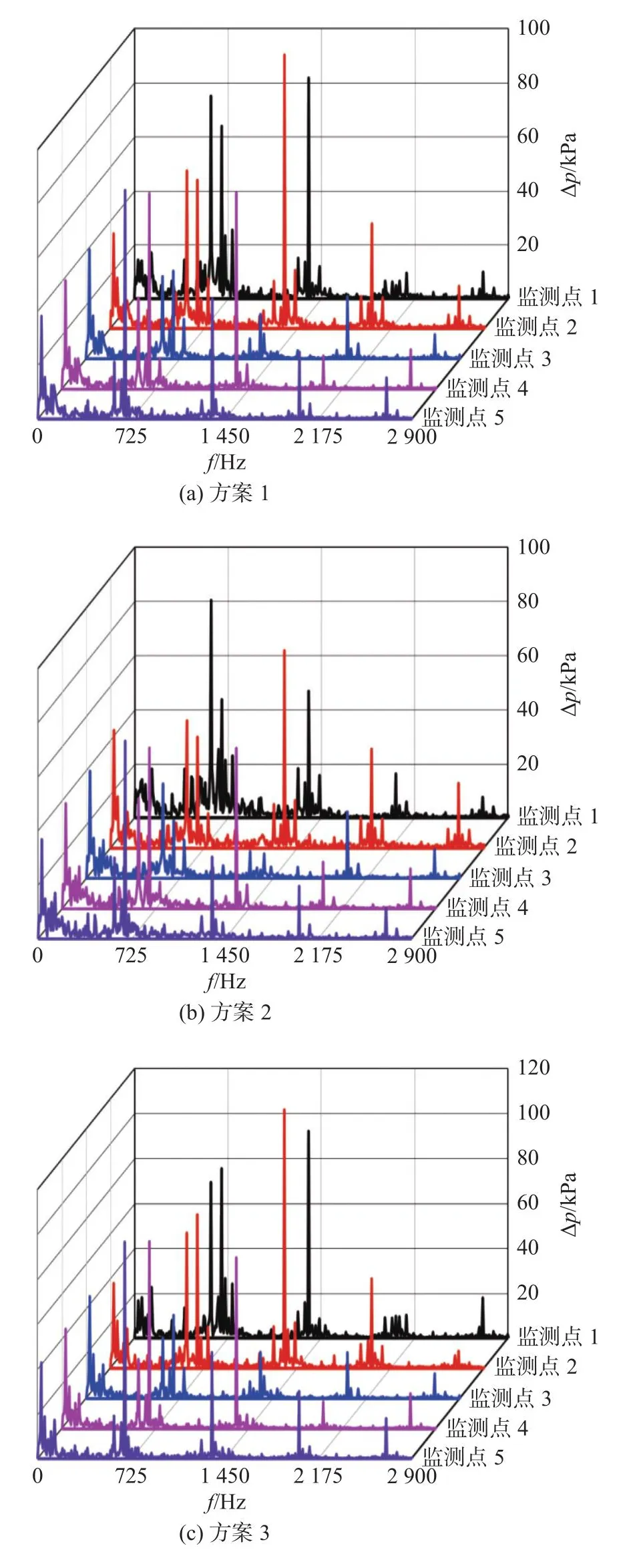
图7 各方案中导叶入口监测点的压力脉动频谱Fig.7 Pressure fluctuation spectra of monitoring points at the inlet of guide vane in each scheme

图8为各方案中第一级叶轮中截面压力分布。从图中可以看出，叶轮出口和导叶入口的狭小间隙内压力分布明显不均。由于叶轮叶片数和导叶叶片数互质，从某一时刻开始，两组叶片正对，随着叶轮的旋转，总有几个时刻，两组叶片正对。也就是说，叶轮叶片和导叶叶片的相对位置在变化，两者之间存在动静干涉。因此，从导叶入口背面到工作面的弧段上压力分布也是不均的，这也是产生如上文所述压力脉动现象的根本原因。

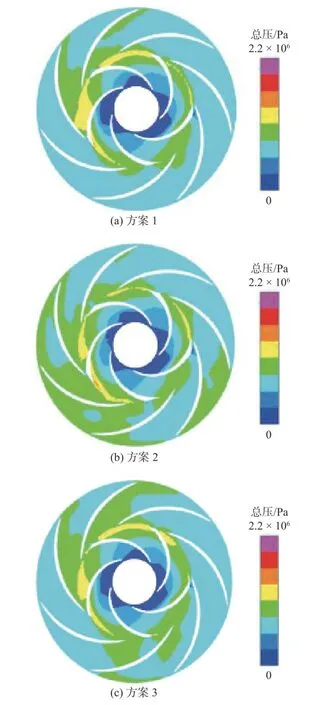
图8 各方案中第一级叶轮中截面压力分布Fig.8 Pressure distribution on the middle cross section of the first stage impeller in each scheme

2.4 流体激励力结果分析

将第一级叶轮受到的空间x、y、z三个方向激励力分别记为F1、F2和F3，各方案中叶轮所受到的三个方向的激励力（三向力）ΔF频域图如图9所示。轴向力的脉动性很小，可以忽略不计。受空化影响，ΔF同样在低频处表现出高幅宽频特征。x、y方向受力相差不大，且脉动主频均为2倍叶频，这与上文分析的结论相同。同样，随着频率的增加其频域幅值依次减弱，直到最后基本为0。方案2中叶轮所受的三向力最小，因此可认为该方案相对最优。

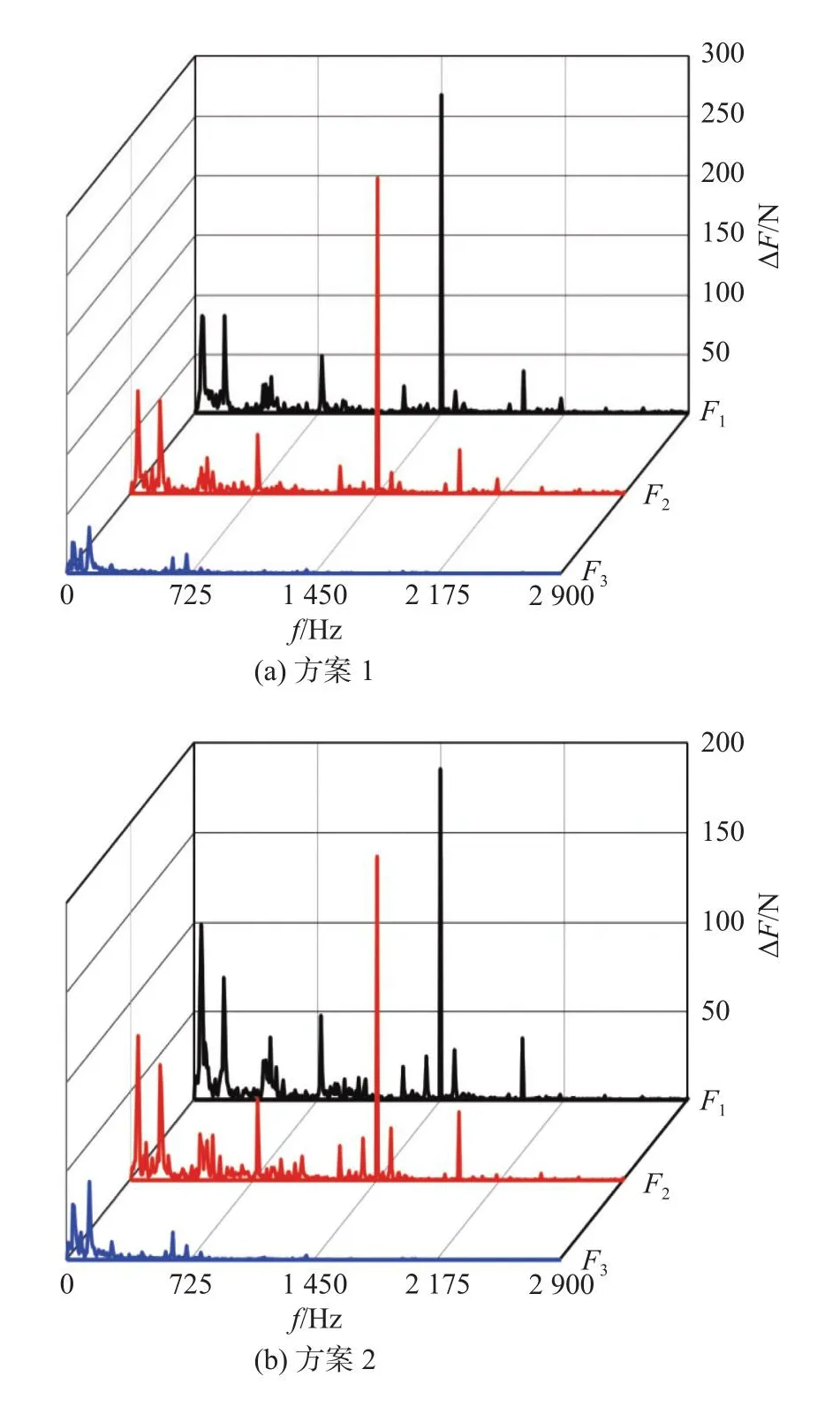
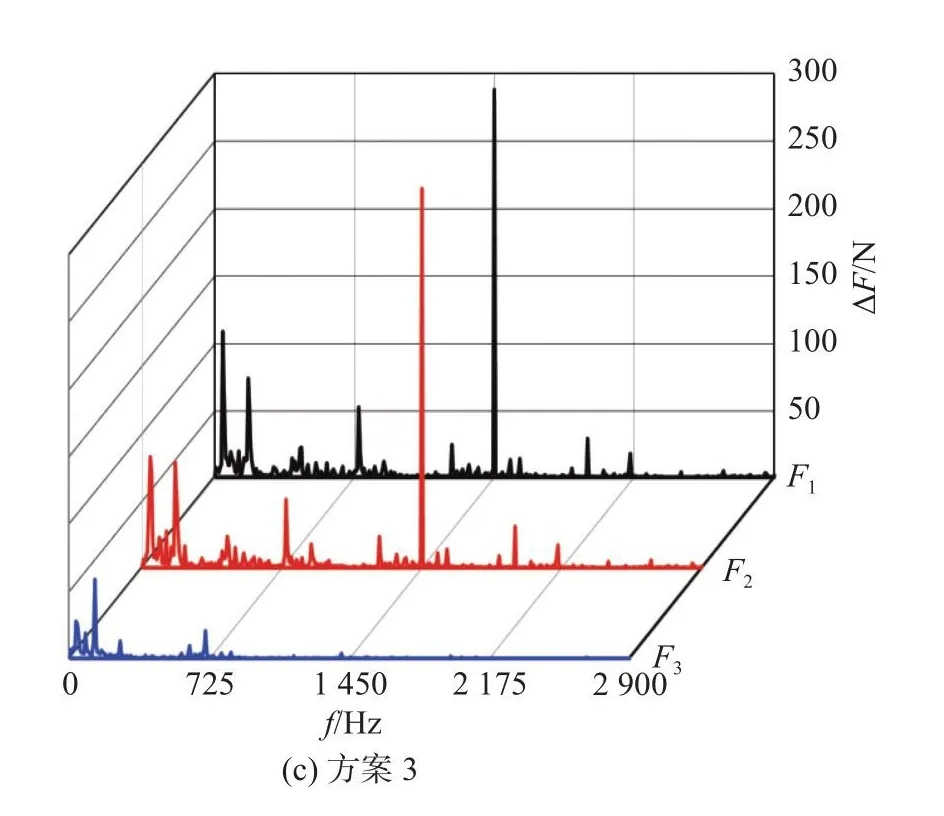
图9 各方案中第一级叶轮受到的空间三向力Fig.9 Three-axis forces on the first stage impeller in each scheme

图10为三种方案中第一级叶轮受到的径向力和轴向力频域对比，其中径向力为叶轮在x、y轴方向受力的合力。由于轴向力较小，在图10（b）中与空化伴生的高幅低频脉动成为波动的主要成分，叶频脉动并不占主导地位。与轴向力相比，径向力的频域图有较大的差别，其在低频处仍然保留宽频特征，725 Hz即叶频处也存在明显的脉动幅值，但是并不占主导地位，波动主频为2倍叶频，且在该处出现双幅值。

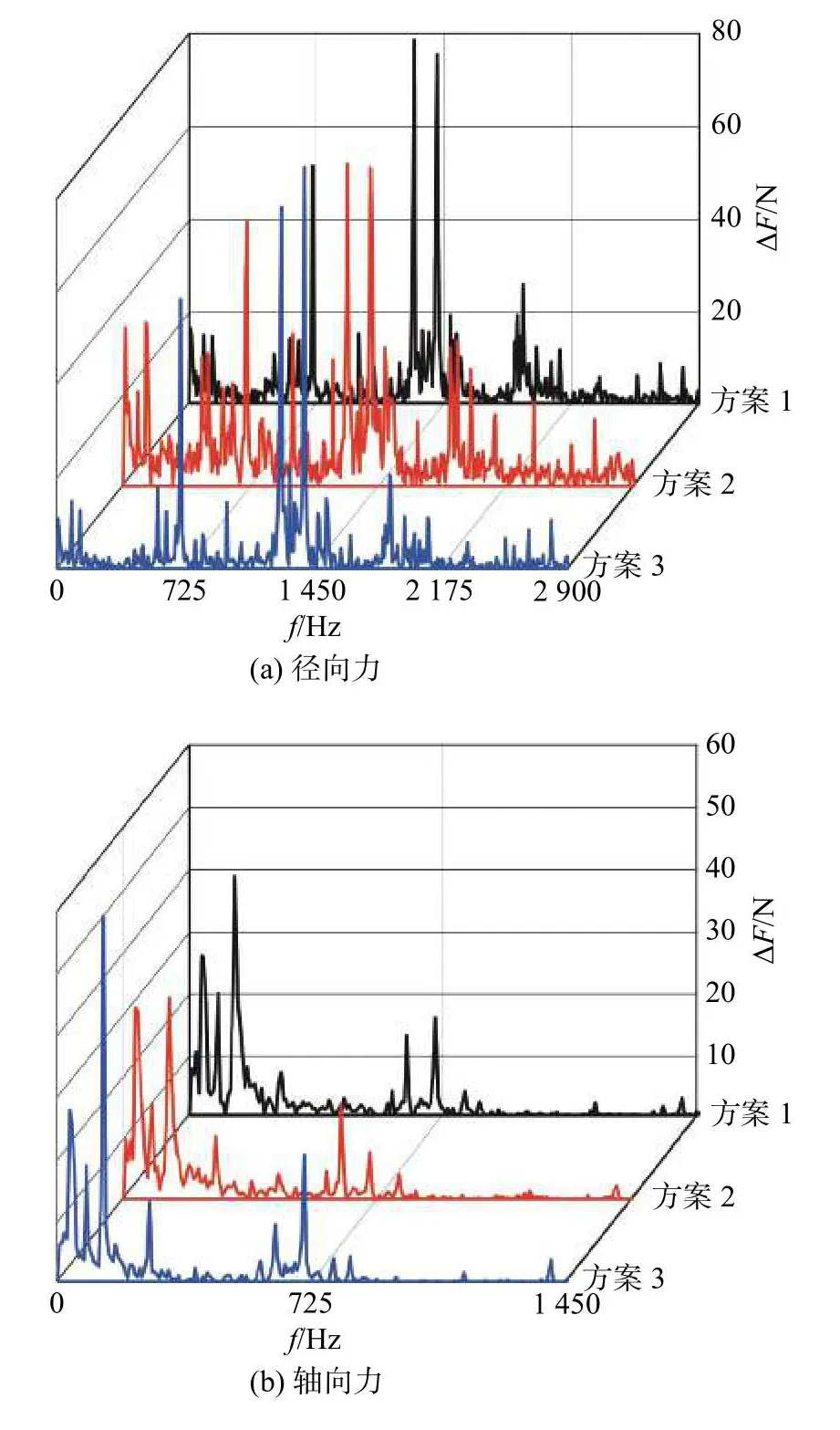
图10 三种方案中第一级叶轮受到的径向力和轴向力频域对比Fig.10 Comparison of radial force and axial force on the first stag impeller in three schemes

3 结 论

本文采用全空化模型和混合流体两相流模型对两级离心泵进行了数值模拟，分析了第一级叶轮叶片厚度分布对空化及非定常流动特性的影响，得出如下结论：

（1）叶片厚度对泵的空化特性有重要影响，采用线性厚度分布的对称叶片时，前缘厚度对空化性能的影响最大，叶片越薄，泵的抗空化能力越强。

（2）第一级叶轮流道内监测点的压力脉动主频为干涉叶频，且保留高幅低频的宽频特征。尾缘越厚，低压区前移，由于空化气体的聚集，使得喉部区域“前移”，即压力脉动幅值向叶轮进口方向偏移。叶片厚度减小，压力脉动幅值相应减小。

（3）第一级叶轮所受空间三向力的脉动主频为2倍叶频，是整个压力脉动的主要成分。轴向力较小，脉动幅值较低，可以忽略不计。径向力的脉动信号较为丰富，主要包括叶频和2倍叶频，但2倍叶频为主导频率。