基于改进NURBS曲线的水下机械臂轨迹规划*

孙颙琰 郭文勇 孙云岭 王晶航

（海军工程大学动力工程学院 武汉 430033）

1 引言

水下机械臂已经越来越多的应用于舰船水下检测与维修［1］，为了水下机械臂能够稳定、快速地完成水下维修任务，满足舰船水下应急维修的需求，基于实验室的六自由度水下机械臂如图1所示，对水下机械臂进行轨迹规划研究。

图1 水下机械臂实物图

机械臂通常主要是在关节空间或笛卡尔空间进行轨迹规划［2］。在关节空间中进行轨迹规划主要是针对机械臂各个关节变量，将关节的位移、速度、加速度等参数表示成时间的函数，由于不需要考虑末端执行机构的运动状态，该方法主要应用在点位控制（PTP）中。在笛卡尔空间中的进行轨迹规划则主要针对末端执行机构得运动状态，将末端执行机构的位姿、速度、加速度等参数表示成时间的函数，该方法适用于连续轨迹控制（CP）中，常运用于对末端执行机构的运动状态有特殊要求的轨迹规划［3］。

笛卡尔空间轨迹规划对于机械臂末端虽然能准确控制位姿、速度等参数，但是在规划过程中需要不断地进行运动学逆解来得到其他关节角，将位姿序列映射成关节角度，而运动学逆解的运算量比正解的运算量大了好几倍，使得求解时间增加，而在关节空间中进行轨迹规划则省去了这一步，使得计算量大量减少，不用考虑奇异问题［4］，还可以直接反映出各关节的参数变换，机械臂各关节的速度、加速度和加加速度等参数在关节空间中实时性更好，且控制和描述更方便［5］，因此本文采用在关节空间下进行轨迹规划的方法。

2 关节空间轨迹规划方法

在关节空间中进行轨迹规划最常用的方法有三次多项式曲线插值、五次次多项式曲线插值、B样条曲线插值和NURBS曲线插值等。

2.1 NURBS曲线插值算法

B 样条曲线是贝塞尔曲线的一般化，就是通过控制点进行局部控制形状的曲线，广泛应用于曲线拟合中。B 样条曲线在保留了贝塞尔曲线优点的基础之上，同时也克服了它的缺点，能够对曲线进行更加方便的控制，在曲线次数较低时仍有较多控制点去控制曲线；可以通过某个控制点去修改局部曲线而不会导致整个曲线形状的发生变化；同时有着更好的凸包性质，对曲线的形状能够进行更加细致的控制。常用于需要经过多个关键节点的轨迹规划中。司艳伟等［6］对通过分析三次B 样条曲线和七次B 样条曲线，证明了三次B 样条曲线比七次B 样条曲线运算效率高，且能够有效的避免龙格现象。Guan Y.S［7］结合三次B 样条四次B 样条曲线的优点，提出了4-3-4 复合轨迹规划方法，该方法在保持较高运算效率的同时，也能够保证加速度曲线的连续性与平滑性，但无法保证加加速度的连续。

NURBS（Non-Uniform Rational B-Spli-nes）即非均匀有理B 样条曲线，最早由美国西拉丘兹大学的Versprille 在其博士论文中提出。波音公司的罗温首先将有理参数曲线曲面引入到了形状设计中，随后，1991年在国际标准化组织颁布的工业产品数据交换标准STEP 中，决定将NURBS 确定为定义工业产品几何形状的唯一数学方法［8］。为解决插值点较远时曲线产生尖点和突变问题，Kubota 等［9］采用三次NURBS 曲线插值进行轨迹规划，发现三次NURBS 曲线能够较好地控制端点，有效地避免了曲线突变，得到的位移、速度曲线平滑无突变。

无论是多项式插值拟合方法还是B 样条方法，都具有很大的局限性［10］，比如对小范围复杂曲线的拟合能力差，范围过大又需要进行分段处理等。将NURBS 曲线应用在机械臂的轨迹规划方法中可以解决大部分问题，NURBS 曲线优秀的局部性能由其定义决定，通过改变任意单个参数对曲线形状的修改，均只影响相应的局部位置，整体性能不变，并且k次NURBS曲线的k-1阶导数连续［11］。为降低轨迹规划所得曲线关节位置的跟踪误差，从而减少机械臂的系统损耗，最终达到延长其使用寿命的目的，所提出的轨迹规划方法须保证结果的位移、速度、加速度平滑并且加加速度连续。故本文采用四阶导数连续的五次NURBS 曲线进行插值轨迹规划。

B样条曲线方程可以表示为

其中di(i=0，1···，n)是控制顶点。Ni，k(u)(i=0，1···n)称为基函数，u为节点矢量，是由非递减的参数组成的序列：u0≤u1≤···un+k+1。

在本文的轨迹规划问题中，用机械臂运行的时间来表示节点矢量。

B 样条有着许多种等价定义，其中最为常用的是得布尔-考克斯递推公式：

由式（2），要确定第i个k次B样条基函数需要k+2 个节点，节点矢量如下：

ui，ui+1，···，ui+k+1

由于求解曲线方程中相应n+1 个控制顶点需要n+1 个k次B 样条基函数，而确定这些基函数所需的节点构成整条曲线的节点矢量U，参数的数量为n+k+2。并且在参数u轴上任意一点u∈[ui，ui+1]处，至多有k+1 个k次B 样条基函数是非零的，即：

Nx，k(u)(x=i-k，i-k+1，···i)≠0

因为适用于自由型曲线的B 样条曲线无法满足初等曲线的要求，于是把B 样条方法改造成为有理B 样条方法来满足使用要求。而在实际应用中，B 样条曲线往往出现非均匀的特性，所以研究者们决定将这种曲线称为非均匀有理B 样条曲线，即NURBS 曲线。之所以在轨迹规划中使用NURBS曲线，是因为NURBS 曲线在进行有理的过程中引入了权因子ω，这就让曲线有了较好的几何解释，并且ω能够影响曲线的局部变化，这一点在轨迹规划中有着重要意义［12］。一条k次NURBS 曲线可表示如下：

由NURBS 曲线的定义可知，确定一条NURBS曲线需要知道节点矢量U 和控制顶点di(i=0，1···，n)，由于本文中的节点矢量代表时间分配，是待优化项，可以先采用平均分配或随机分配的方式给定初始值，确定NURBS 曲线后再对时间进行优化。所以，再通过已给定曲线需要经过的路径点求出出NURBS 曲线的控制顶点，就能够画出NURBS曲线。

给定m+1 个需要经过路径点qi，其中i=1，2，···，m-1。为方便计算取ωi=1。

则k次B样条曲线方程就可以简写为

由于控制顶点d0和dn分别与路径起点q0与终点qm重合，故d0和dn两个控制点已知，还需求出n-1 个未知控制顶点。将节点值带入式（4），即：

由式（5）可得n-k=m+1 个方程，分别对应m+1 个路径点。另外，轨迹始末速度和加速度的方程如下：

其中、为关节初始速度与加速度，、为其关节停止时速度与加速度，一般均设置为0。

于是现有n-1 个未知参数，n-k+4 个方程，当k=5 时，位置参数与方程式数相等，故当使用5次NURBS 曲线对关节位置进行插值所得轨迹曲线时，可以将初始速度与加速度、停止速度与加速度作为边界条件。由曲线特性可知，五次NURBS 曲线是C4连续的，可以满足加速度与加加速度曲线连续的要求。根据给定轨迹点可以求出NURBS 曲线的全部n+1 个控制顶点。再根据式（3）得到五次NURBS曲线方程。

2.2 基于五次多项式速度控制的NURBS 曲线插值算法

通过NURBS 曲线插值算法得到曲线，会产生曲率突变，曲线峰值过高现象，导致机械臂速度突变，抖动严重，甚至超过机械臂的加减速度的最大范围，从而无法完成规定轨迹。为改进一般NURBS 曲线插值算法的缺点，提出一种基于五次多项式速度控制的NURBS 曲线插值算法，简称QV-NURBS曲线插值算法。

该改进算法首先通过NURBS 曲线插值得到轨迹曲线，然后通过分析曲率的变化情况找到特征点，将曲线分成曲率平缓段和曲率突变段，通过对曲率突变段的曲线进行分析，获该突变段的速度、加速度以及加加速度等参数，采用五次多项式对该段进行速度规划控制，利用式（7）的C4连续性，通过控制速度使得曲率突变段更加平滑，实现在突变段能够稳定运行，以保持机械臂全程的稳定性。

该算法分为5步：

1）根据式（2）和式（3），由给定的时间节点矢量和轨迹点求出NURBS曲线。

2）扫描特征点。特征点包括曲线间断点和曲率突变点。曲线间断点一般位于节点处，能够通过节点矢量得到，不在节点处的大曲率点可以利用式（7）进行判定得到。

其中，ρi为第i各插值点的曲率半径。

3）判断相邻特征点的速度规划交叉类型。当两相邻特征点之间的曲线弧长出现较小情况时，一般由于加速度限制，速度就无法加速至最大。两相邻特征点的速度轨迹规划就出现了交叉区域。具体分为以下七种类型［13］。

类型1：速度轨迹规划无交叉区域。其中为第i-1 个特征点加速度阶段的位移，为第i个特征点减速阶段位移，Si为第和第i个特征点间的曲线弧长。

4）针对上诉7种类型进行速度规划。

（1）若判定为类型1，则加速至最大速度Vmax后，然后保持匀速运，最后到减速点后减速。

（2）若判定为类型2或类型5，速度加速到Vi后减速。Vi可以使用二分法［14］计算得到。

（3）若判定为类型3或类型4，以起始特征点开始，按照五次多项式轨迹曲线运动至终止特征点，其中五次多项式曲线的起点、终点速度与起始、终止特征点的速度相同。

（4）若判定为类型6或类型7，则把此类特征点从特征点序列中除去。

5）得到经过五次多项式速度控制的NURBS 曲线，即QV-NURBS曲线。

3 轨迹规划算法仿真分析

通过表1中的D-H 参数，利用Robotic Toolbox建立机械臂仿真模型，如图2。机械臂执行一段曲线轨迹，起点A 坐标为（0.557，-0.134，-0.289），终点坐标为（-0.458，-0.028，-0.395），通过逆运动学方程求解出各关节对应的关节角度如表2。

表1 水下机械臂D-H参数

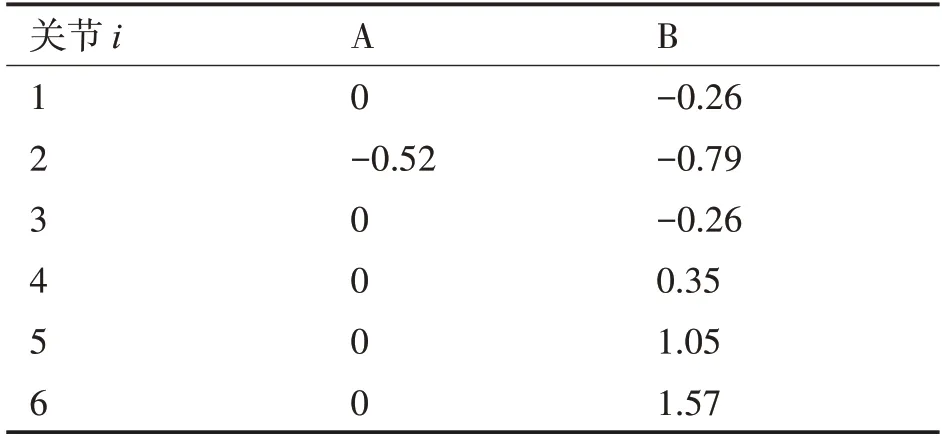
表2 起点与终点的各关节角

图2 水下机械臂仿真模型

要求机械臂末端从A 点运动到B 点，运动时间为5s，初始速度和加速度、终止速度和加速度均为0，然后运用五次多项式插值和QV-NURBS 曲线插值进行轨迹规划。其中通过五次多项式插值得到机械臂各个关节角度位移、速度、加速度以及加加速度曲线如图3所示。

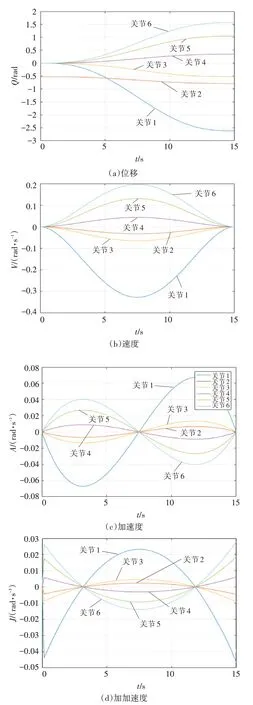
图3 五次多项式插值各个关节角度位移、速度和加速度曲线

通过图3可知，五次多项式插值的位移、速度、加速度曲线光滑连续，无突变，但是加加速度曲线初始有突变，但后续也能保持光滑连续且无突变，能够保证机械臂较为平稳的运行，但在初始阶段机械臂所受冲击较大。

通过QV-NURBS 曲线插值对路径点进行轨迹规划，得到机械臂各关节角度位移、速度、加速度和加加速度曲线如图4所示。

图4 QV-NURBS曲线插值各个关节角度位移、速度和加速度曲线

通过图4可知，QV-NURBS 曲线插值算法可以使得机械臂各关节的位移、速度、加速度以及加加速度曲线光滑连续且无突变，使得机械臂能够在运行轨迹的整个过程中保持运动的平稳性。

通过对两种种插值算法的仿真对比可知：两种插值算法均能保持位移、速度曲线的连续平滑；对于加加速度曲线，五次多项式插值在启动阶段有突变，但在运行阶段可以较好保持平滑，QV-NUBRS曲线插值则可以很好的保持曲线全程平滑。综上所述，QV-NUBRS 曲线插值可以解决起始位置的震动和运行过程的不平稳问题，从而完成对各关节运行角度、速度以及加速度的连续有效控制。

4 结语

对关节空间中NURBS 曲线插值算法进行公式推导，并针对NURBS 曲线插值算法的缺点进行改进，提出了QV-NURBS 曲线插值算法，并建立该插值算法在六轴水下机械臂轨迹规划中的数学模型。

对机械臂轨迹规划的两种插值算法进行Matlab 仿真分析，对比优劣性，结果表明基于QV-NURBS 曲线插值的轨迹规划，使得机械臂末端运行稳定，轨迹平滑连续，任意一条路径都可以采用QV-NURBS 曲线插值的方法进行规划实现，为水下机械臂试验验证以及机械臂控制系统的设计奠定了基础。