面向数据挖掘的网络流量分析及预测研究综述*

肖军弼 魏娇娇

（中国石油大学（华东）计算机科学与技术学院 青岛 266580）

1 引言

近年来，随着Internet 网络结构不断复杂化发展，以及各种网络设备类型不断涌现，网络用户的规模也在不断提高，这使得网络流量数据急剧增加，同时对网络的有效管理、负荷评估和安全预警带来了新的挑战［1］。在传统方法下网络流量特征被描述为线性相关的，然而，在现代网络环境下的网络流量呈现出多种复杂的非线性特征，如具有长相关性、自相似性、时变性、突发性、混沌性等特点［2］。面对如此复杂的网络环境，开展网络流量分析研究具有重要意义。

网络流量特性分析是进行网络流量分类及预测研究的前提与关键，分析出网络流量所具备的特性，根据其特性的变化规律，选择出一种计算量相对较小、结构简单的分类与预测模型。

通过网络流量分类研究，网络监管部门对正常流量和恶意流量进行准确、及时的分类识别，可以有效避免恶意流量对用户带来的干扰和损失［3］。同时，网络流量分类与识别在病毒入侵检测、访问认证授权等方面也发挥着重要作用［4］。在网络流量分类研究中，传统的基于特定规则的分类方法随着网络流量数据规模越来越大，流量组成越来越复杂，已经不能满足当今的网络流量分类需求，基于数据挖掘的网络流量分类方法［5～6］已经成为目前的研究热点之一，如许多学者采用有监督学习的网络流量分类方法，例如利用朴素贝叶斯（Naïve Bayes，NB）［7］、支持向量机（Support Vector Machine，SVM）［8-9］、决策树（Decision Tree）［10］、神经网络（Neural Network，NN）［11～13］等算法进行网络流量分类研究，还有学者将KNN［14～16］、K-means［14，17～18］、隐马尔科夫算法（Hidden Markov Model，HMM）［19］等无监督学习的网络流量预测方法应用于网络流量分类，此外，还有学者提出了使用基于高斯混合模型（Gaussian Mixed Model，GMM）［20］、基于半监督支持向量机（Semi-Supervised Support Vector Machine，S3VM）［21］等基于半监督学习的分类方法［22］。

通过开展网络流量预测研究，网络管理者可以实时掌握网络运行时的状态，优化网络资源分配，检测潜在的网络威胁与故障，以便提前采取措施进行干预［23～24］。随着网络流量特性愈发复杂，传统的线性模型难以准确地进行预测。近年来，许多学者和研究者开始将数据挖掘技术如支持向量机（SVM）［25］、神经网络（NN）［26～28］、长短期记忆神经网络（Long Short-Term Memory，LSTM）［29～30］、梯度提升树（Gradient Boosting Decision Tree，GBDT）［31］、决策树（Decision Tree）［32～33］、灰色模型（Grey Models，GM）［34］等与网络流量预测研究相结合，并通过实验证明这些算法能够有效提高预测精确度。

2 网络流量的特性及其分析方法

2.1 网络流量的特性

1）自相似性

网络流量的自相似特性［35］是指网络流量时间序列在时间维度上表现出在不同时间尺度下具有相同或者相似的统计特征。以下是该特性的统计学方法描述。

假设一个随机过程X(t) ，t∈R，对于所有a＞0 均满足式（1），则称X(t)是自相似系数为H的自相似过程。

其中，a表示随机过程的时间尺度变化，为渐进同分布，H为自相似Hurst参数。网络流量的自相似程度可根据参数H值来描述，H值的具体取值范围是[0 ，1] ，其大小反映了网络流量自相似性的强弱程度［12］。当0 ＜H＜0.5 时，表明该流量序列有较弱的自相似性。当0.5 ＜H＜1 时，表明该流量序列有明显的自相似性，且越接近1，该流量序列的自相似性就越强。因此，可以通过计算网络流量时间序列的Hurst值来判断该序列是否具有自相似性以及强弱程度。

2）长相关性

网络流量的长相关性［36］是指某一时刻的网络流量值与此时刻之前的所有时刻的网络流量值之间具有一定的关联性。以下是该特性的统计学方法描述。

如果随机过程X=Xt，t=1，2，…，n的自相关函数x(k)满足以下公式，则称该随机过程具有长相关性。

其中，x(k)是自相关函数，ρk是自协方差函数，E(X)是均值函数。

3）突发性

网络流量数据的突发性［37］是指网络流量在某一时刻急剧上升或下降，网络流量产生突变性的原因主要是某一时刻用户行为的频繁变化和网络设备的急剧增多引起的，比如大量用户在同一时刻访问相同的网站、某一时刻同时接入大量网络设备等。

4）周期性

网络流量的周期性［38］是指在一定时间范围内的不同时间区间里流量具有相似甚至相同的变化趋势，并且这种趋势会反复出现。在网络管理过程中，可以根据网络流量的周期规律规划网络资源使用情况，提高管理效率。

5）混沌性

网络流量的混沌性［39］是一种类似无规则的、随机的现象，既包含有序序列，又包含无序序列。即网络流量数据实际上是混杂着低维混沌噪声数据的时序序列。

2.2 网络流量的特性分析方法

网络流量的特性决定了其行为表现，准确地分析其特性有助于构造合适的分类与预测模型，进一步获得准确的分析结果。所以十分有必要在开展流量分析之前，先分析一下流量的基本特点。表1给出了主要的网络流量的特性分析方法的优缺点及适用范围。

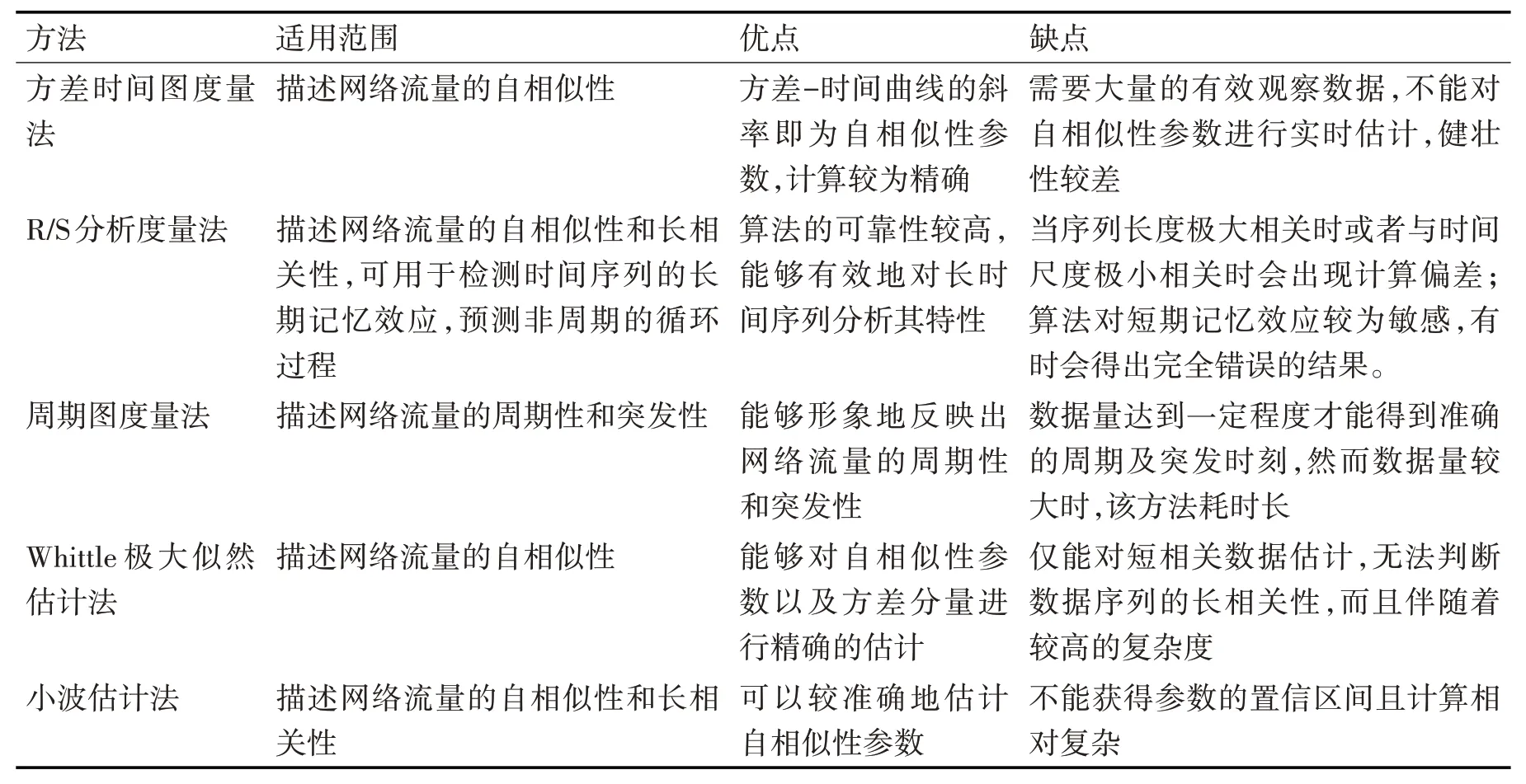
表1 网络流量特性分析方法及其特性

3 网络流量分类

3.1 网络流量分类方法的评价指标

定义TP（True Positive）表示正确分类的真例数量、TN（True Negative）表示正确分类的假例数量、FN（False Negative）表示错误分类的假例数量、FP（False Positive）表示错误分类的真例数量。

1）召回率（Recall）。召回率是TP占实际真例总数的百分比，其定义如下：

2）精确度（Precision）。精确度是TP占分类为真例个数的百分比，其定义如下：

3）F 值（F-Measure）。F-Measure 是精确度、召回率的调和平均数，结合了两者的评价标准，其定义如下：

4）准确率（Accuracy）。网络流量分类方法的准确率计算方式如下：

3.2 传统的网络流量分类方法

传统的网络流量分类研究通常采用基于特定规则的方法，比如基于端口的分类方法［40～41］与基于深度包检测［42～43］的分类方法。这类方法的特点是由人工制定规则，并且将规则进行硬编码，通过匹配硬编码的固定规则划分出网络流量类别。然而由于流量剧增及特性日益复杂化使得这类方法不再适用于当前的网络流量分类研究。

3.3 基于数据挖掘的网络流量分类

3.3.1 有监督学习的网络流量分类方法

有监督学习是指训练有输入有输出的样本。表2 给出了主要的基于有监督学习的网络流量分类方法及其特性。

表2 有监督学习的网络流量分类方法及其特性

3.3.2 无监督学习的网络流量分类方法

基于无监督学习的网络流量分类算法是通过聚类的形式来划分数据集包含的所属类，通过某种方法，在学习过程中会将特征相似的样本归为一类。此类算法的优点是具有发现新型网络应用的能力。主要的基于无监督学习的网络流量分类方法如下。

1）KNN 算法［14～16］。该算法理解简单，且模型的训练时间短。但是在进行网络流量分类时，需要计算测试集与训练集内部数据之间的相似度，计算成本高，并且在训练过程易受到噪声数据的影响。此外，由于该算法对所有的训练数据进行保存，导致内存占用大。

2）K-means 算法［14，17～18］。该算法的优点是结构简单、容易理解，并且当密集数据的类与类之间的区别明显时，能够得到很好的分类效果。但是K-means 算法中初始均值向量K 的选定是难以估计的，算法的计算时间长，当K 值选择不当时会产生很大误差，并且对异常数据在计算质心的过程中，会对结果产生很大的影响，容易陷入局部最优。

3）隐马尔科夫（Hidden Markov Model，HMM）聚类算法［19］。该算法是一种时序相关的概率模型，首先基于隐马尔科夫链生成一个不可观测的状态序列，然后根据状态序列生成预测结果。但该模型在进行网络流量分类的应用过程中具有一定缺陷，按照HMM 算法的假设，该模型不能记忆上下文信息，因此分类结果只与其前一个状态信息关联，若想利用更多的已知信息，必须建立高阶HMM模型，然而高阶模型会导致算法的复杂度较高。

3.3.3 半监督学习的网络流量分类方法

基于半监督学习的分类方法中，训练数据由大量未标记数据和少量已标记数据构成，训练过程结合了有监督学习与无监督学习的思想。半监督学习分类方法的优点是训练方法对已标记的数据的依赖程度较低。目前也有研究将这种方法应用于网络流量分类研究，比如：

1）基于高斯混合模型（Gaussian Mixed Model，GMM）的半监督分类算法［20］。该方法的优点是可以很好地描述时序数据的特征，通过收敛准则逐步迭代可以更好地拟合数据。但是该方法往往只能收敛于局部最优。

2）基于半监督支持向量机（Semi-Supervised Support Vector Machine，S3VM）的半监督分类算法［21］。该方法是利用了结构风险最小化计算方法进行网络流量分类，S3VM 假设决策超平面与无标签数据的空间分布信息的分布情况一致，然而如果实际情况不满足此假设，构造的决策超平面会产生较大误差，最终导致性能变差。

4 基于数据挖掘的网络流量预测

4.1 网络流量预测的评价指标

1）均方根误差（Root Mean Square Error，RMSE）。该值反映出流量预测值与真实值之间的距离，用于评价网络流量数据的变化程度，如果该值越小，说明当前的网络流量预测模型性能越优。RMSE 对异常大或者异常小的预测误差尤其敏感，这使其可以较好地反映预测精度。该评价指标的计算方法如式（9）所示：

其中，表示流量预测值，yj表流量实际值，n代表评估的数据总量。

2）测定系数（R-Squared，R2）。该值反映的是预测的准确率，取值范围是0～1，该值越大，说明当前的网络流量预测值的准确率越高。计算公式如式（10）所示：

3）模型的训练时间。在对网络流量数据进行预测的研究中，机器学习模型需要使用大量资源来建模，因此，在进行模型训练的过程中，需要考虑计算成本，而模型的训练时间在模型的计算成本中占据重要影响。

4）平均绝对百分比误差（Mean Absolute Percentage Error，MAPE）。该值是统计上常用于评估模型预测精确度的一个指标，该值越小，则表明预测的结果就越好。计算公式如式（11）所示：

其中，表示流量预测值，yj表流量实际值，n代表评估的数据总量。

5）准确率Accuracy。计算公式如式（12）所示：

其中，X表示真实流量矩阵，表示预测流量矩阵。

4.2 基于单个模型的网络流量预测方法

表3 给出了主要的单个网络流量预测模型的特性及其适用场景。

表3 流量预测模型特性

4.3 基于混合模型的网络流量预测方法

随着网络复杂化，应用多样化，网络流量的非线性特征愈发明显，网络流量序列的长相关性、周期性、突发性等特点使得单一的网络流量预测模型难以准确地进行预测。研究者开始将多种分析方法与网络流量预测模型相结合，并且通过实验证明组合预测模型能够有效提高预测精确度，有着良好的拟合与预测效果。例如文献［44］提出基于SVM进行预测，结合遗传算法进行优化，结果发现在流量预测方面整体性能较优，且具有较高的精度。文献［45］提出布谷鸟搜索算法与支持向量机算法相结合的网络流量预测模型（MCS-SVR 模型），并且在同一个数据集上分别与利用遗传算法和粒子群算法优化的SVM 算法做对比实验，实验结果证明MCS-SVR 模型提高了网络流量预测精度。文献［46］提出一种基于深度置信网络的预测算法，同时融入无监督学习的自动编码器AE，实验结果表明，该算法具有较好的预测性能。文献［47］提出使用灰狼算法优化支持向量机算法的参数并结合LSTM算法来建立网络流量预测模型，通过实验证明该混合模型能够有效处理非线性序列预测问题，并且具有很强的容错能力，预测精度较高。文献［48］提出一种残差卷积和循环神经网络相结合的无线网络流量预测模型，该模型能够精确提取网络流量数据的时空特性，实现了对流量的有效预测，并且设置了流量监控异常报警机制，加强了网络流量的管理与规划。文献［49］提出一种图卷积神经网络结合门控循环神经网络的混合流量预测模型，该模型基于图卷积层来提取SDN流量复杂的空间相关性，通过门控循环单元来提取SDN 网络流量的时间相关性，将空时关系相结合来进行SDN 网络流量预测，并且通过实验证明了该混合模型具有良好的性能。

5 结语

本文从网络流量特性分析、网络流量分类、网络流量预测三个方面分析了网络流量分析的研究现状，介绍了当前网络流量分析的研究内容，总结了近几年常用于网络流量分类和网络流量预测的数据挖掘方法。明确了高效的网络流量分析研究具有重要意义：有助于对网络进行更好的规划和优化，实现网络问题的提前预警，保证网络系统安全、稳定运行。但是在现有的网络流量分析的研究中，也存在一些有待解决的问题，如在对原始网络流量数据进行预处理时，预处理的结果会直接影响到模型的预测性能；使用特定的算法进行网络流量特征提取时，若模型结构的复杂度较高及模型参数的选择不当，会导致较高的成本问题。在未来的研究中，建立结构复杂度相对较低、计算量较小的分类与预测模型，同时将所提出的模型实际应用于现实场景中是网络流量分析预测研究中需要进一步考虑的问题。