基于BP神经网络的碳达峰目标下碳汇计量方法研究
陈书忠 赵泉
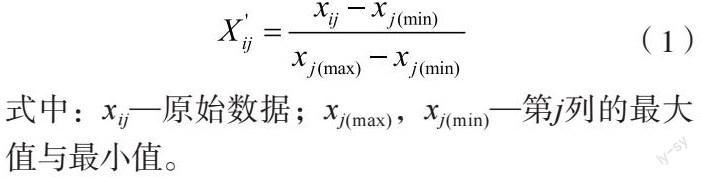

摘 要:为了解决当前碳汇计量方法存在计量误差、准确率低的问题,提出了基于BP神经网络的碳达峰目标下碳汇计量方法的研究。首先,基于碳达峰目标对碳汇数据进行预处理,获取准确度较高的碳汇数据;根据BP神经网络构建碳汇计量BP神经网络模型,输出碳汇数据集;然后综合考虑碳库选择指标,选择与碳汇数据集匹配的碳库;最后,实现碳达峰目标下碳汇计量的目标。实验证明,此种计量方法具有较高的拟合度,计算值与原值更加接近,相对误差在1.01%~1.71%,始终保持在2%以下,证明该方法的碳汇计量结果准确率较高。
关键词:BP神经网络;碳达峰;碳汇计量;准确率;拟合度;碳库
中图分类号:X38 文献标志码:A 文章编号:1673-9655(2023)01-0-05
0 引言
在全球经济体系快速发展的趋势下,人们对资源的需求量不断提高。由于各个行业领域不断地开采自然资源,为企业带来经济效益的同时,也容易产生一定的环境污染,使生态环境中的碳系统失去平衡,导致温室效应加剧[1]。为了降低碳的排放,应当采用一定的措施控制气候变化,实现碳排放达到峰值的目标[2]。碳达峰指的是二氧化碳在某个区域或一定的时间范围内排放量最高,达到了历史最高值,经过一段平台冷静期后,逐渐转化为持续下降的过程[3]。碳达峰作为监测二氧化碳排放量变化的一个拐点,标志着二氧化碳排放量由上升趋势转换为下降趋势[4]。根据碳达峰目标的不同,将碳达峰划分为两种:碳达峰年份与碳达峰峰值[5]。通过碳达峰的情况,能够判断碳中和的程度,两者之间具有一定的关联,碳达峰年份与峰值直接影响着碳中和的速度与效率[6]。在碳汇研究力度不断加大的背景下,碳汇经济发展的速度不断加快,为企业带来经济效益的同时,也对生态环境产生了较大的影响,碳汇计量方法能够估算碳排放量,评估经济与环境的發展。
有研究学者提出基于多目标模型的碳汇计量方法,以我国主要耗煤产业、电力、供热、交通以及碳汇量为研究对象建立多目标模型,实现碳汇计量[7]。但是这种方法无法在碳达峰目标下获取精准的评估结果,准确率较低,失去了计量的意义。基于此,本文结合了BP神经网络,提出了在碳达峰目标下碳汇计量方法的设计。
1 基于BP神经网络的碳达峰目标下碳汇计量方法设计
1. 1 碳达峰目标下碳汇数据预处理
碳汇储存量不仅包括自身的碳储量,在一定程度上还包括其他物质释放的碳储量。受到自然环境与其他因素的影响,对碳汇计量的准确度造成一定的影响,因此,应当首先对碳达峰目标下碳汇数据进行预处理[8]。BP神经网络包括多个单元模块,单元模块经过组合,能够与多个领域交叉应用,帮助领域解决部分复杂的难题。BP神经网络具有较广泛的适用范围,在应用过程中具有能力强、效率高以及执行力强的优势[9]。碳汇计量方法作为评估项目环境与经济效益的重要基础,在计量单位与属性上具有较高的要求[10]。
本文设计的基于BP神经网络的碳达峰目标下碳汇计量方法,能够对各种环境下的碳汇数据进行分析,通过一定的处理方式,生成符合碳达峰目标的碳汇数据。数据中各指标的量纲或数量级不同,在实质性处理之前,需要对碳达峰目标下碳汇数据进行预处理,去掉其量纲,将这些数据统一在[0,1]或[-1,1]这个区间内。将数据通过归一化方法进行处理,计算公式如下:
为了降低由于天气情况等不利因素对碳汇计量结果产生的影响,在获取碳汇数据时,尽量选择天气情况较好的时间[11]。采用MATLAB数据获取工具,将观测到的碳汇数值以原始图像的形式加载到数据获取工具的figure中,输入相应的指令,获取碳汇数据点在图像中的坐标,基于比例换算的方式,获取相关的二氧化碳通量,作为BP神经网络的主要数据。
在获取到碳汇数据后,由于二氧化碳通量形成于呼吸作用与光合作用中,应当对碳汇数据进行过滤处理,避免碳汇数据出现明显的浮动现象,缩小数据的变化范围。
对BP神经网络的收敛速度进行相关控制,对BP神经网络的训练时间进行严格的规划与记录,保证碳汇计量结果的客观性[12]。采用规范化算法,对碳汇数据进行变量转换处理。给定一个变量 f,设置f的值域范围在0到1之间,设定min和max分别表示变量f的最小值与最大值,基于规范化算法,转换f的变量形式,计算公式为:
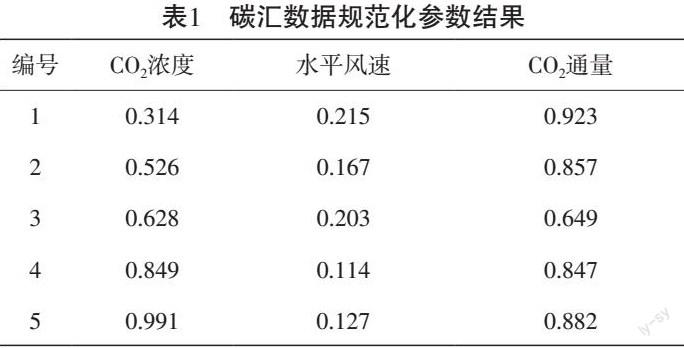
式中:xif—变量f的碳汇度量值,变量 f 包括二氧化碳的浓度、水平风速、二氧化碳通量和植物光合速率,经过上述公式的转换,获取到碳汇数据的规范化参数结果,如表1所示。
如表1所示,为本文获取到的经过预处理的碳汇数据规范化参数,在进行碳汇计量方法时,应当严格按照表1的参数进行操作。
1. 2 建立碳汇计量BP神经网络模型
基于上述碳达峰目标下碳汇数据的预处理结束后,为了提高碳汇计量结果的准确率,结合BP神经网络的特征与优势,共同建立BP神经网络模型。通常情况下,碳汇计量中涉及的因素较多,包括二氧化碳浓度、平均风速、二氧化碳通量、植物光合速率等,因此,在建立模型时,综合考虑上述影响因子对计量结果的影响。设置二氧化碳、水平风速和植物光合速率作为BP神经网络模型的基本输入;模型的输出只有一种,即二氧化碳的通量。本文将碳汇计量的BP神经网络模型结构进行了划分,具体划分为输出层、中间层与输入层三种结构。在模型中,ρc表示二氧化碳的浓度;w表示水平风速,ρd表示植物光合速率;Fc表示输出端二氧化碳的通量。设置神经网络模型的中间层为单层结构,在中间层中包含若干个节点,根据碳达峰目标下碳汇训练的样本量、模型的收敛速度,确定BP神经网络模型输入层最终的节点个数。
模型在训练样本量的学习训练过程中,输入层进行单向传播,输入的数据为二氧化碳的浓度与实际的水平风速,输出变量与输入变量的形式不同,输出变量通常在单向中间层中进行传播,输出的数据仅由二氧化碳通量组成,具有较好的泛化能力。BP神经网络模型在训练样本数量方面没有限制,能够快速地获取二氧化碳通量与各个影响因子之间的变化情况,模型的收敛速度具有较大的优势。本文设计的碳汇计量BP神经网络模型的运行流程,如图1所示。
如图1所示,首先,在模型中输入碳汇数据集,根据数据集的具体特征,分为训练数据集与测试数据集。结合离散数据网格化的算法,对BP神经网络中的碳汇数据进行排序,将模型训练样本量的数据样本进行分组处理,划分为A、B两个组,根据具体的分组情况,初始化神经网络模型,当模型读入第一个样本数据时开始相应的训练;采用算法计算出模型中输出量的输出误差,判断误差是否达到碳汇计量的精度要求,达到要求则得出最终的碳汇训练数据,达不到则返回重复上一步模型操作,直至最终达到碳汇计量精度要求为止。
接下来,要确定神经网络模型中间层节点的个数,节点的个数与碳达峰目标下碳汇计量的结果具有一定的关联。模型中间层节点个数设置过少,会降低模型训练样本的归纳与反映效果,无法清晰地获取碳汇数据样本集的变化规律;节点个数设置过多的话,在碳汇计量中会形成过量拟合的现象,降低BP神经网络模型的泛化水平,导致模型训练的时间较长,影响碳汇计量的效率。本文采用交叉验证的方式确定模型中间层的节点个数,重复训练BP神经网络模型的各个单元,保证充足的模型单元循环次数。
设置模型中的碳汇数据样本容量为500,在样本进行训练时,设置模型各个单元的学习率为0.75,模型运行的精度控制参数为0.001,在BP神经网络模型中进行拟合运算,控制拟合运算的循环次数不少于1000。结合BP神经网络惯性系数,提高神经网络模型的收敛速度与效率,避免在碳汇计量过程中出现模型训练时间过长的情况。基于神经网络算法,计算出BP神经网络模型在每次训练后的单元误差值,计算公式为:
式中:Zij—模型运行中输出矩阵的任意元素,在本文中表示二氧化碳浓度、水平风速;e—模型训练后的单元误差值;Yj—模型单元中的样本输出,即二氧化碳通量。
通过公式(3)获取到BP神经网络模型在每次训练后的单元误差值,将误差值返回到模型的上一层,与输出端结果相对比,修改单元误差值的权值,最终输出模型的碳汇数据集。
1. 3 选择碳库
根据上述建立的碳汇计量BP神经网络模型,获取到符合碳达峰目标的碳汇数据集,选择与碳汇数据集相匹配的碳库,提高碳储量的精确度。想要实现碳汇计量的目标,最常用的方法就是对项目边界内所有类型的碳库进行计量,然而,此种计量方法在一定程度上增加了项目的成本,消耗大量的人力与资源。因此,本文对此种方法进行了改进,选择一个具有代表性的碳库或者一系列主要碳库,通过估算碳库中碳存储量的变化量,实现碳汇计量的目标。由于不同碳库中碳储存量存在一定的差异,根据地理环境与自然条件的不同,碳储存量也不同,基于此,在碳库选择中,本文结合了土地利用系统的优势进行选择。
在选择过程中,综合考虑碳汇计量的成本,如果计量成本过高,对项目的顺利开展会产生较大的影响。碳库的选择具有一定的指标,包括碳汇计量项目的类型、碳汇计量成本以及项目对碳汇计量结果精度的要求。基于碳库选择指标与碳储存量的变化量,共同选择碳汇计量所需的碳库。
1. 4 碳达峰目标下碳汇计量
碳汇计量主要是对碳储量及储量变化量进行估算,计量方法的种类较多,本文采用项目碳储量变化量计量方法实现碳汇计量。项目碳储量变化量主要包括碳库中各个项目碳层生物量变化的和,减去项目引起的其他生物量碳储量的降低量,计算公式为:
式中:ΔC1—第t年碳达峰目标下碳储量的具体变化量;ΔC2、ΔC3、ΔC4和ΔC5—第t年碳达峰目标下,i碳层中碳储量变化量、生物量碳储量变化量、地下生物量碳库中碳储量的降低量和地上生物量碳库中碳储量的降低量;t—碳达峰目标下碳储量开始的年数;i—项目碳储量的碳层。
在碳库中随机设置几个小样方,采用收获法获取项目碳储量中的含碳率平均值,结合物质的量计算方法,获取项目边界内各层计量碳库基线的具体数据信息。在满足碳汇计量精度的情况下,设定碳层内样方的形状与面积相同,固定样方的数量,基于有效性计量原则,最终获取碳达峰目标下碳汇计量结果。
2 实验分析
2. 1 实验准备
基于上述的設计,为了进一步对本文设计的基于BP神经网络的碳达峰目标下碳汇计量方法作出客观的分析,采用本文设计的方法,对绿地碳汇进行计算。
选取本市郊区某校园绿地作为实验的目标对象,以该绿地2018—2021年汇总数据为本文实验数据,对该绿地的碳汇进行计算。将二氧化碳浓度、水平风速和植物光合速率作为BP神经网络模型的网络输入数据,以二氧化碳通量作为网络输出,进而训练网络。
构建BP神经网络模型,作为本次实验的核心模型,模型结构如图2所示。
本文构建的BP神经网络模型数据信息与误差均为单向传播的方式,数据信息通过正向传播,误差通过反向传播。
设置输入模式向量为X=(x1,x2,…,xn);希望输出向量为Y,将输入层的节点数设置为n,均匀分布在模型的隐含层中,其大小形态完全不同,Wa=(a=1,2,…,n)表示模型中输出层到第a节点的权值,Wta(t=1,2,…,n;a=1,2,…,n)表示输入层第t节点到隐含层第a节点的权值。隐含层各单元输入向量为B=(b1,b2,…,bn);输出层输入向量为L=(l1,l2,…,ln),输出向量为C。
调整神经网络预测的非控制性变量,进而推算出控制变量,作为本次实验碳达峰的预测分析。本次实验在总数据中选取2018—2020年数据作为训练样本,输入碳汇训练数集到模型中,结合最速下降的方法,对误差的反向传播方式进行设置,同时调整迭代次数,改变神经网络权值。通过反向传输的方式,调整神经网络的权值,减小输出向量与期望的向量之间的差值,提高计量结果的精度。将本文设计的BP神经网络隐藏层确定为6层,隐藏层中神经元为12个,对应该绿地碳排量主要因子,该绿地通过 tansig函数进行激活,学习速率设置为0.5,迭代训练次数为1500次,输出层为1个神经元,对应该工厂碳排量,以此检验BP神经网络模型的有效性。经过1500次训练后,得到神经网络模型的权值阈值结果如表2所示。
2. 2 结果分析
设置本文提出的基于BP神经网络的碳达峰目标下碳汇计量方法为实验组,将基于多目标模型的碳汇计量方法为对照组,对比两种碳汇计量方法计算结果的相对误差,将该绿地2021年数据作为测试样本,结果如表3所示。
根据表3可知,作为对照组的基于多目标模型的碳汇计量方法的计算值与原值之间差距较大,相对误差在3.64%~11.77%,波动较大;而本文提出的基于BP神经网络的碳达峰目标下碳汇计量方法的计算值与原值更加接近,相对误差在1.01%~1.71%,始终保持在2%以下,波动较小,并且误差率较低,说明本文提出方法计算结果的准确率较高,更加具有优势。
3 结束语
本文设计的基于BP神经网络的碳达峰目标下碳汇计量方法的计量结果准确率较高,具有一定的优势。本文设计的计量方法能够有效地推动我国高新技术产业的发展,具有较高的拟合优势,能提高各个领域能源的利用率,实现碳系统的平衡发展。然而,本文在碳汇计量属性方面的研究仍然存在一定的不足,在未来应当加以改进。
参考文献:
[1] 钟薇薇,高海,徐维军,于孝建.多聚类视角下的碳达峰路径探索与趋势研判——基于广东省21个地级市面板数据的分析[J].南方经济,2021(12):58-79.
[2] 盛伟,李峰,肖楠.高效碳中和示范林选择及计量监测技术[J].现代农村科技,2021(12):104.
[3] 关琰珠,钟寅翔,吴毅彬,陈澜韵.科技创新与碳达峰碳中和目标下区域碳排放与污染物协同减排的调控政策研究——以厦门市为例[J].中国发展,2021,21(5):79-88.
[4] 丁爽,姜玲玲,林翎,杨波,等.我国碳达峰碳中和标准化发展现状及对策研究[J].中国标准化,2022(1):63-70,75.
[5] 胡剑波,赵魁,杨苑翰.中国工业碳排放达峰预测及控制因素研究—基于BP-LSTM神经网络模型的实证分析[J].贵州社会科学,2021(9):135-146.
[6] 范德成,张修凡.基于PSO-BP神经网络模型的中国碳排放情景预测及低碳发展路径研究[J].中外能源,2021,26(8):11-19.
[7] 王深,吕连宏,张保留,王斯一,等.基于多目標模型的中国低成本碳达峰、碳中和路径[J].环境科学研究,2021,34(9):2044-2055.
[8] 王勇,许子易,张亚新.中国超大城市碳排放达峰的影响因素及组合情景预测—基于门限-STIRPAT模型的研究[J].环境科学学报,2019,39(12):4284-4292.
[9] 高鸣,张哲晰.碳达峰、碳中和目标下我国农业绿色发展的定位和政策建议[J].华中农业大学学报(社会科学版),2022(1):24-31.
[10] 刘梅影,罗斌华,苏利阳,刘扬.国家生态文明试验区(江西)推进碳达峰、碳中和的进展、挑战及对策分析[J].环境保护,2021,49(Z2):74-76.
[11] 李绥,石铁矛,王梓通,李滔,等.基于建筑容量的城市建设用地碳汇量核算方法[J].应用生态学报,2019,30(3):986-994.
[12] 段福梅.中国二氧化碳排放峰值的情景预测及达峰特征—基于粒子群优化算法的BP神经网络分析[J].东北财经大学学报,2018(5):19-27.

