基于自适应滑模控制器的机械臂运动控制方法①
谷 龙
(合肥通用职业技术学院,安徽 合肥 230031)
0 引 言
机械臂是一种复杂的系统,具备精度高、耦合程度强、非线性、灵活的操作性等显著特征,可在一定设定的程序下完成目标的执行[1]。机械臂可高效地完成作业,因此在诸多领域被广泛应用。但由于该系统的复杂性,在其自身多输入和输出的特性下,其在执行作业过程中,系统参数的设定、环境因素的干扰等因素的影响,会导致机械臂的动力学建模存在明显的不确定性,导致机械臂的控制存在一定误差,对机械臂的空间运动轨迹产生直接影响[2],甚至发生无法准确完成目标作业。机械臂的轨迹跟踪,是其在运动过程中的一种重要控制,该控制可保证机械臂按照理想轨迹完成运动[3]。滑模控制是通过滑膜控制器实现机械臂系统状态的转换,变成切换超平面后,在控制作用下使机械臂达到系统原点,该控制策略可较好地改善机械臂的不确定性,并有效抑制其非线性特征[4]。本文以提升机械臂的运行轨迹跟踪效果为目的,提出基于自适应滑模控制器的机械臂运动控制方法,滑模控制器能够有效的抵制干扰,降低系统抖振,保障系统稳定性,同时降低经济成本,实现机械臂运动过程中不确定因素的抑制,实现机械臂运动轨迹的精准跟踪控制。
1 自适应滑模控制器的机械臂运动控制
1.1 机械臂的动力学模型
1.1.1 机械臂位姿分析
机械臂位姿分析是其动力学建模的基础[5],文中采用矩阵法完成机械臂位姿分析OB。设p表示任意一点,其属于坐标系{A}中,且为直角;为描述其位置,采用3×1的位置矢量表示,用图1描述其位置。
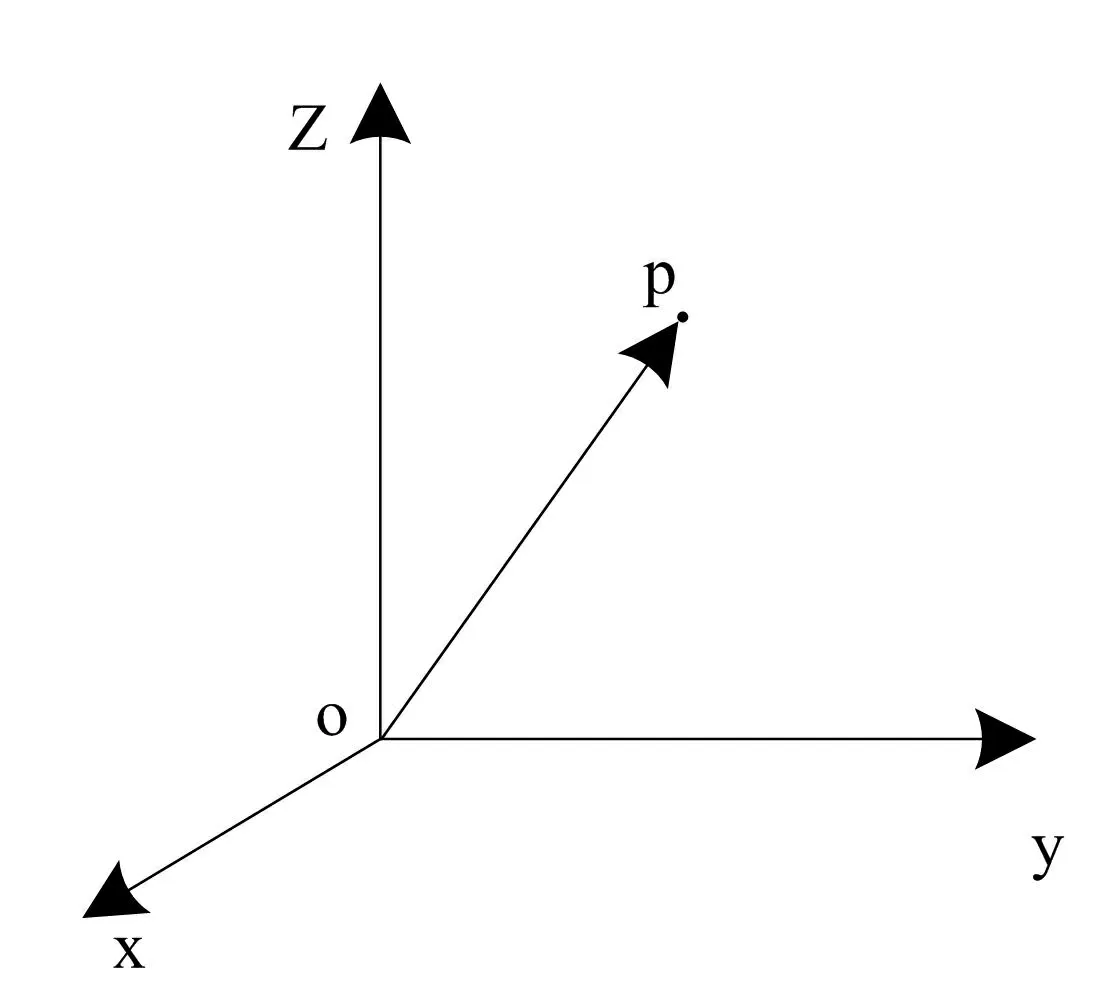
图1 位置描述
该位置矢量公式为:
(1)
式中:p的坐标分量分别用px,px,px表示,属于x,y,z轴上。
采用机械臂的固定连接坐标表示物体方位,设置新的直角坐标系为{B},其用于表示刚体B在空间内的方位,用图2描述。
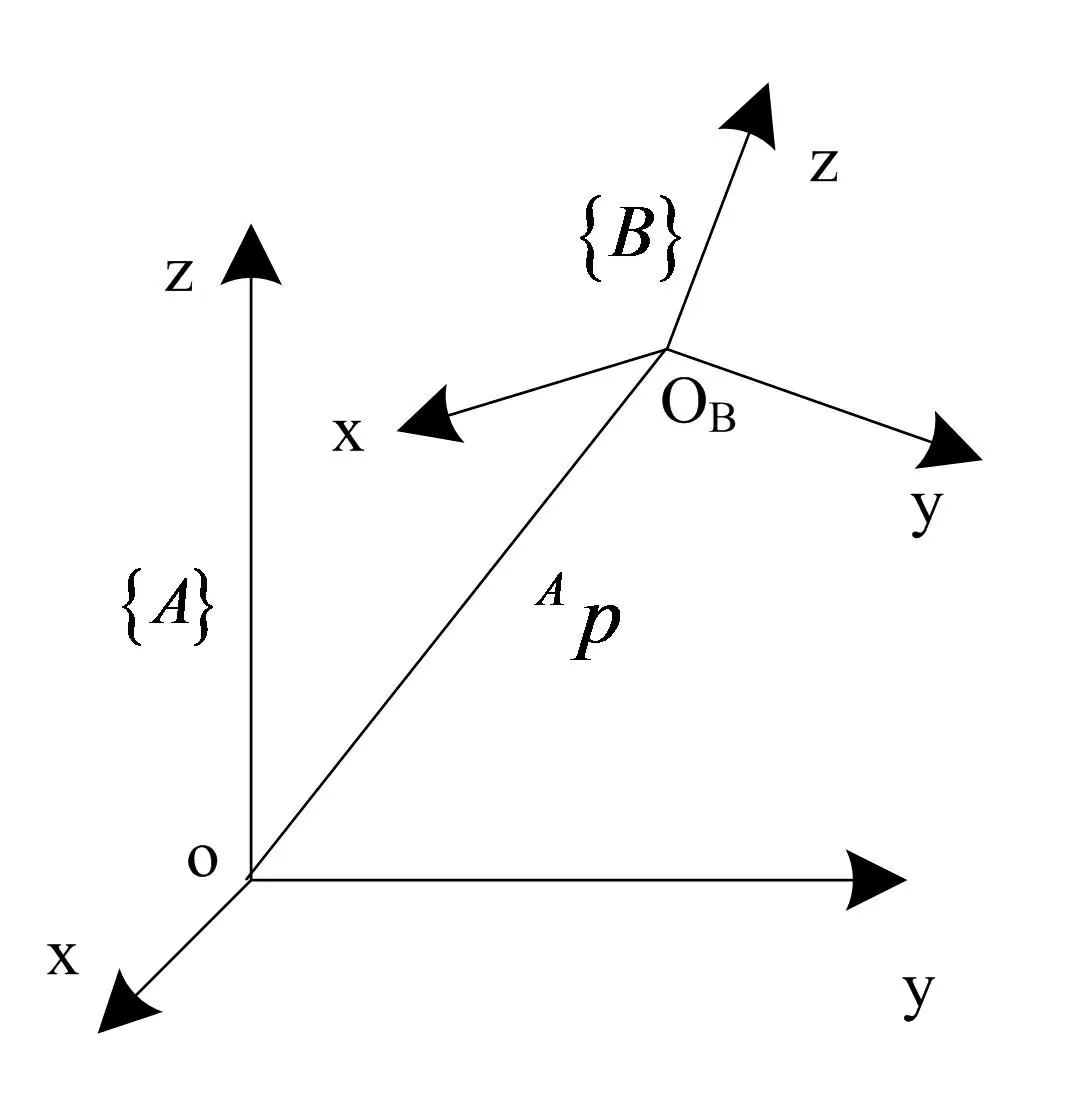
图2 刚体的方位
单位矢量用xB,yB,zB表示,其属于{B}。以{A}为参照,则{B}的位置计算公式为:
(2)
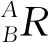
AxB·AxB=AyB·AyB=AzB·AzB=1
(3)
AxB·AyB=AyB·AzB=AzB·AxB=0
(4)
(5)
以角度θ实行B的旋转,且在x,y,z轴上,则三者的旋转矩阵用公式(6)~(8)表示:
(6)
(7)
(8)
机械臂方位的描述需通过设定参考坐标系{A}完成,ApB0则表示原点的某个位置矢量,且属于机械臂坐标系{B},因此,机械臂的方位计算公式为:
(9)
在表示位置和方位时为:
(10)
ApB0=0
(11)
1.1.2 机械臂的抖震处理和补偿
在机械臂工作过程中可产生多种抖震信号,此部分信号即便进行滤波处理,也无法去除其内部的震动,严重地影响了信号的使用效果,为此,将通过提升机械臂构固有频率的方式,降低其惯性,避免机械臂在应用过程中出现形变问题。在原有的基础上增加阻尼器,将此设备的阻尼系数提供一个等级,以此实现低震动、高质量的信号收发。设定正道信号表示为u(t),n(t)表示阻尼系数,重新得到信号为:
v(t)=u(t)+n(t)
(12)
在对机械臂驱动器的信号滤波与防震荡处理后,出现了大量不可执行的信号,导致机械臂无法完成应有的指令要求,为了提升机械臂的控制能力,将对此部分信号进行补偿,通过计算,在原有的信号中插补多条相似指令,使其贴近原始指令,计算公式如下:
(13)
式中,σ2表示方差均值;a为常数值。此时得到的信号在进行输出,能够有效的控制机械臂。
1.1.3 动力学模型
拥有n个关节的机械臂动力模型计算公式为:
(14)
式中:g(θ(t))表示离心力,角位置、角速度和角加速度属于机械臂关节分别表示为:
(15)
其中矩阵表示为:
(16)
依次分别对应正定惯性、哥式力和控制输出,均属于机械臂。
由于机械臂的动力学方程较为复杂,其各个关节均和重力以及摩擦力等因素对应,则方程中的项数会随着关节数量的增加而增加,并且各个关节间的耦合关系也较为显著,需要确定上界信息;外加多种不确定因素均会对机械臂的控制造成不同程度的影响。因此,为了更好地完成机械臂运动轨迹跟踪,其动力学模型中应引入各类不确定性,将上述不确定性均看作外部扰动,则模型的公式为:
(17)
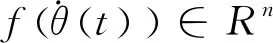
1.2 机械臂运动控制
1.2.1 机械臂运动轨迹跟踪控制器
控制输入的τ,是机械臂运动轨迹跟踪控制目标,该控制可保证机械臂的位姿误差e接近零[6],则针对随意的初始误差可表示为:
(18)
为提升机械臂运动轨迹跟踪控制效果,结合滑膜控制和自适应模糊控制方法,两者结合后设计机械臂的运动轨迹跟踪控制器,其整体结构用图3描述。该控制器无需过多系统信息,未知参数的实时估计可通过模糊规则完成,同时,该规则个估计e和其变化律[7];为保障精确的跟踪机械臂参考轨迹,需有效控制其在运动过程中的抖动现象,可通过控制律增益的逼近实现,且其输入采用模糊系统自适应完成。
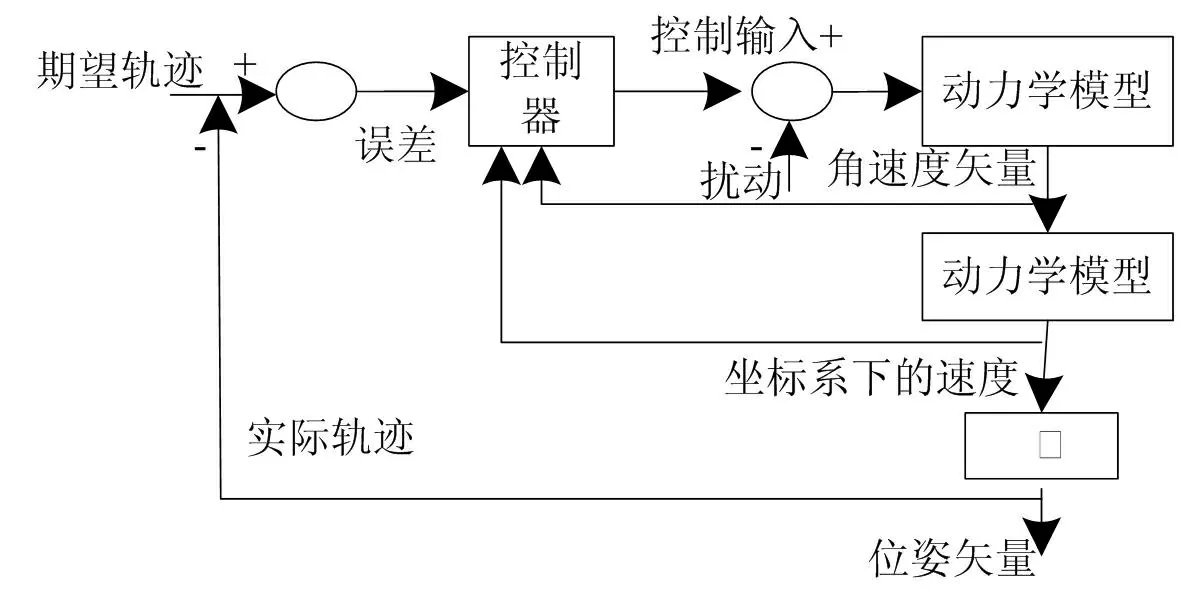
图3 机械臂的运动轨迹跟踪控制器结构
1.2.2 基于模糊增益自适应调整的滑膜控制
通过设计模糊增益调整控制律,实现切换增益的自适应调整,该控制律公式为:
(19)
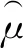
为保证机械臂的稳定性,引入李亚普洛夫函数,其为:
(20)
对公式(13)实行求导,且为对时间,在不对K实行模糊逼近的情况下,将其代入式(11)得出:
V1=sTMs=sT[-(μ+H)s+Δf-K]=
sT(Δf-K)-sT(μ+H)s=
(21)
根据式(14)可知sT(μ+H)s恒大于零,所以符合siki≥0,如果想要V1的取值不为正,则si,ki两者的符号需一致。除此之外(siΔfi-siki)的值也对机械臂的稳定性存在直接影响,如果要V1为较大的非正数,|ki‖随着|si‖的增加而增加,随其减小而减小。
1.2.3 模糊规则设计
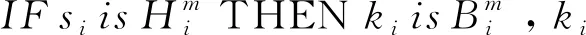
(22)
式中:α和σ表示常数,属于μH(si),则模糊系统的输出公式为:
(23)
式中:M表示模糊规则数量;θki表示矢量,属于可调节参数;ψki表示模糊基矢量。
2 测试结果与分析
为了验证研究方法的可行性,选取两关节机械臂作为测试对象。在定位实验中,通过调节软件设定固定的机械臂位置,对实验样品进行测定,将实测轨迹与预设轨迹进行对比,将两轨迹之间差异作为实验结果输出,以此完成实验实施过程。该测试采用仿真模拟的方式完成,利用Simulink工具完成测试对象的轨迹跟踪控制仿真,机械臂初始状态和外界干扰为:
z(0)=[0,2,1.5,-1]T
τd=[-sint,3cost,-2sint,sint,-cost]T
(24)
机械臂的相关参数为:移动平台质量、两节机械臂连杆质量分别为51kg,4.1kg,3.6kg;三者的转动惯量分别为1.528(kg.m2),0.14(kg.m2),0.147(kg.m2)械臂连杆长度分别50cm,35cm。依据参数通过模拟获取θL,θR,θ1,θ2的跟踪曲线,将其与实际曲线相比较,分析本文方法的控制效果,结果用图4、图5描述。根据测试结果可知:本方法在对机械臂运动控制过程中,两轮的角度跟踪和两节连杆的角度跟踪的初始位置的误差明显,但是均可在0.5s内完成参考轨迹跟踪拟合,可实现机械臂运动的有效控制。
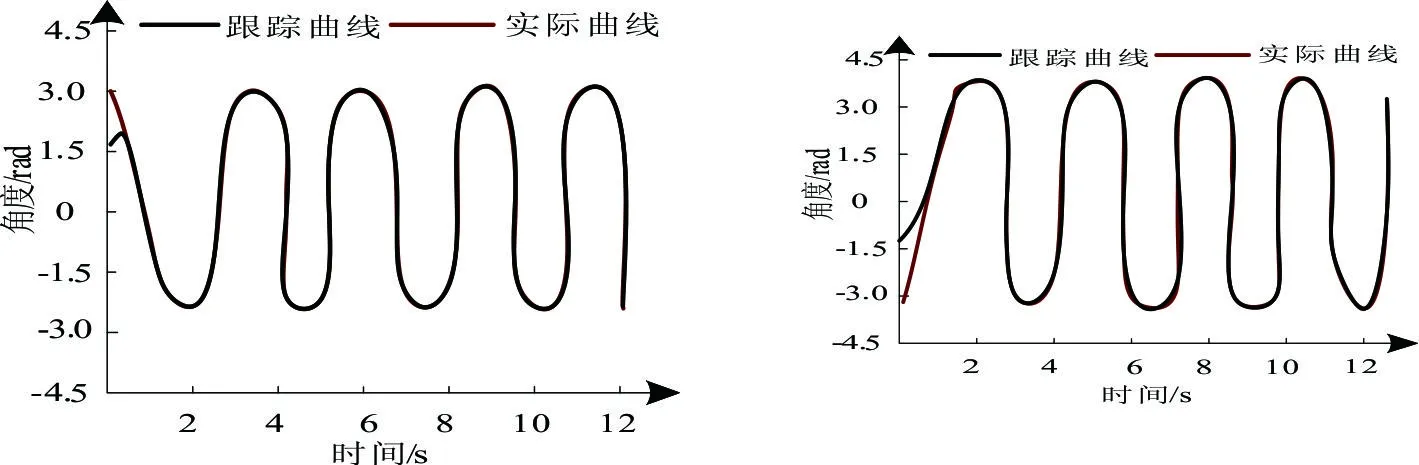
(a)左轮角度跟踪结果 (b)右轮角度跟踪结果
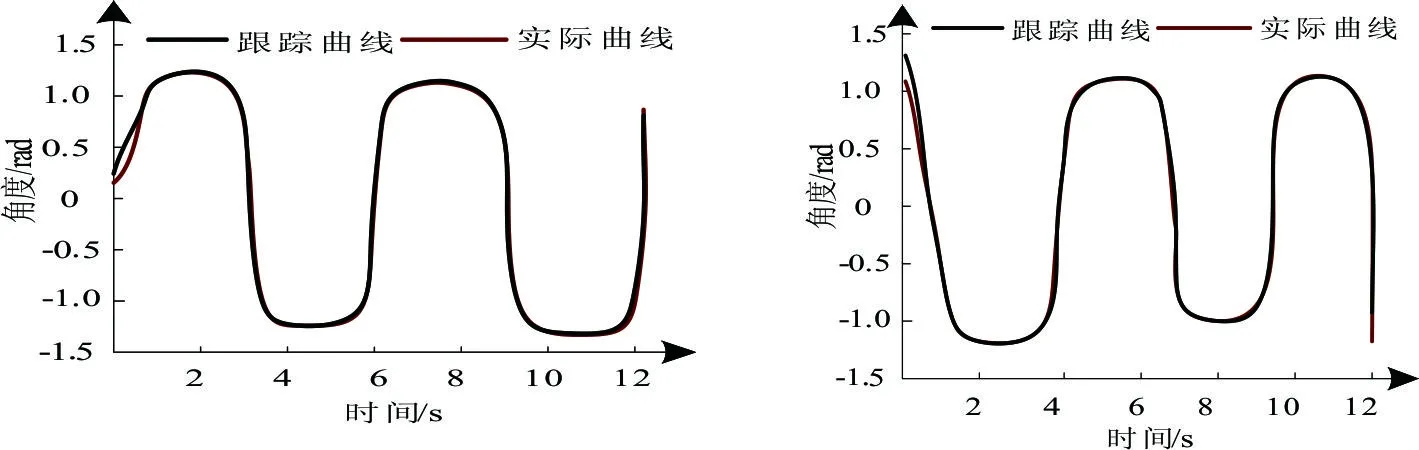
(a)关节1连杆的角度轨迹跟踪结果 (b)关节2连杆的角度轨迹跟踪结果

图6 机械臂控制输入曲线
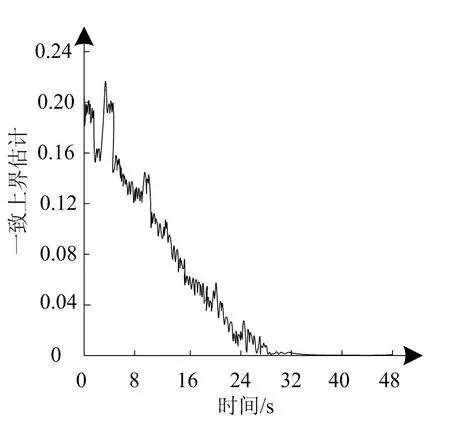
图7 系统参数上界估计曲线
机械臂控制系统的参数在线估计,可降低控制系统在运算过程中,参数较多造成干扰,为测试本文方法的抗干扰性能,通过自适应律完成机械臂控制输入和一致上界估计曲线的获取,以此衡量本文方法的抗干扰性能,结果用图6、图7描述。根据图6和图7测试结果可知:文本方法可在系统已知信息较少的情况下,实现未知参数的实时估计,使机械臂控制系统在运算过程中,面临参数发生变化的情况下,依旧可实现扰动信号一致上界的估计,具备较好的抗干扰能力,可在1.3s内有效控制力矩,有效抑制机械臂抖动现象,实现机械臂的位姿误差最小化。
为进一步分析本文方法的控制效果,测试机械在圆形轨迹和直线轨迹两种情况下的跟踪控制结果,以位置最大误差和标准差作为衡量标准,结果用表1描述。根据表1测试结果可知,本文方法大幅度降低了误差,减小了干扰,从而使机械臂的控制更加精准,效果更佳。
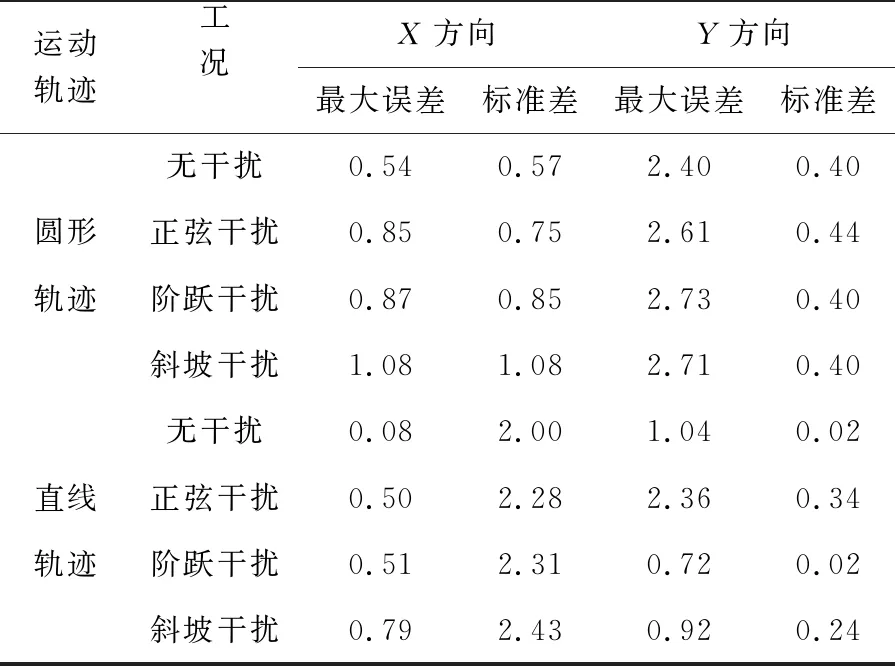
表1 本文方法两种轨迹的跟踪控制误差结果(cm)
3 结 语
机械臂运动的精准控制,是其完成目标的依据,为实现机械臂在不确定性的情况下,依旧能够较好地控制,提出基于自适应滑膜控制器的机械臂运动控制方法,对机械臂的运动轨迹实行跟踪控制。经测试:本文方法可通过自适应模糊控制,有效抑制控制过程中的抖动现象,可在较小的误差下完成期望轨迹跟踪,保证机械臂的位姿误差最小化,可完成不同工况下运动轨迹的跟踪。后期会针对该系统的稳定性和有限时间的收敛性进行研究分析,使系统更佳完善。

