智能家居中的网络路由改进算法研究①
朱丽华, 林 平
(池州职业技术学院,安徽 池州 247000)
0 引 言
智能家居系统是以住宅为平台,利用计算机技术、网络通信技术、综合布线技术、传感器技术、安防技术等打造高效、舒适、安全、智能的人文居住环境[1]。在智能家居中,所有的家庭硬件设备都基于无线传感器网络[2]的搭建而连接的,在搭建网络时,其路由算法相关的分析结果,和网络运行成本密切相关,并且影响网络效率等问题,因而算法研究极为受关注[3,4]。路由算法作为智能家居网络的核心问题,直接影响了网络的服务质量和用户的体验感。
1 网络路由优化算法
网络路由协议常用的度量一般包括以下6个方面[5]:路径长度(又称为跳数);可靠性;时延;带宽;负载;通信开销。一直以来,研究人员在网络路由算法方面做了大量的研究工作,也获得相应的成果。如N.R. Wankhade[6],Huang C F[7]研究得到了免疫克隆算法,模拟具有免疫系统的生物在细菌入侵的过程中自身免疫细胞对抗原做出免疫并产生抗体的过程,将网络路由上一次计算的最有路径进行保存,在下一次的计算过程中自动以上一次的计算结果为约束条件进行重新选路,大大提高了计算速度,但是全局搜索能力并不理想。P. Tian[8]等学者按照牛顿下山法,改进提升了克隆免疫算法,以获得更为优异的全局搜索性能,不过计算效率明显下降。王莉[9]在其研究中,则按照蚁群算法,对网络路由技术进行了分析,不过出现了局部最优化的问题。文献[10]通过对蚁群算法的深入研究,分析了蚁群算法在网络路由协议中的应用,建立了基于蚁群算法的模型,优化了网络路由的路径,但忽略了网络的费用问题。文献[11]提出一种优化的蚁群算法,并建立了带约束的网络模型,虽然优化了网络服务质量,但该蚁群算法增加了网络负载,计算复杂度也比较高。在无线传感器网络中,网络路由协议不仅要保证网络内节点的信息传输准确、高效和稳定,传输路径还要满足通信开销损耗小的条件[12]。Si J[13]等人将BFA(Bacterial Foraging Algorithm,细菌觅食算法)应用到计算机网络中的路由问题中,经比较,细菌觅食算法在精度和计算速度上优于传统算法。
2 算法思想
通过对已有的研究成果分析,传统、单一的算法应用在网络路由算法在通信开销、可靠性、计算效率等方面均达不到理想效果。通过对细菌觅食算法、免疫算法、蚁群算法和BFA等深入分析研究,结合了融合半解析解的内容[14],就算法的具体操作步骤进行了分析,得到了GFBA算法技术,该算法在细菌的趋向性、复制、迁移三个操作环节进行了重新的整合和调整,迁移的步长值可以随着计算的进行而改变,用免疫算法(generate and test)代替BFA的复制操作环节,在迁移操作环节中,对适应度最高的个体被驱散的概率进行调整。最后利用GFBA算法,建立网络模型,并针对路由优化问题进行实验仿真,从计算速度、全局搜索能力、计算精度方面验证GFBA算法对于网络路由问题的适用性和优越性。
一般BFA算法里如果其随机数要比迁移概率更低,就能完成细菌迁移,而迁移的目的是为了避免出现局部最优解问题。按照这种处理方法,会影响全部细菌,具有良好适应性的细菌,基本都能完成迁移。GFBA算法进行迁移时,适应性最理想的细菌个体,驱散概率是零,而如果该参数能达到,就能让搜索效率提升。
3 算法实现
基于算法思想,对于该算法的具体步骤如图1所示。
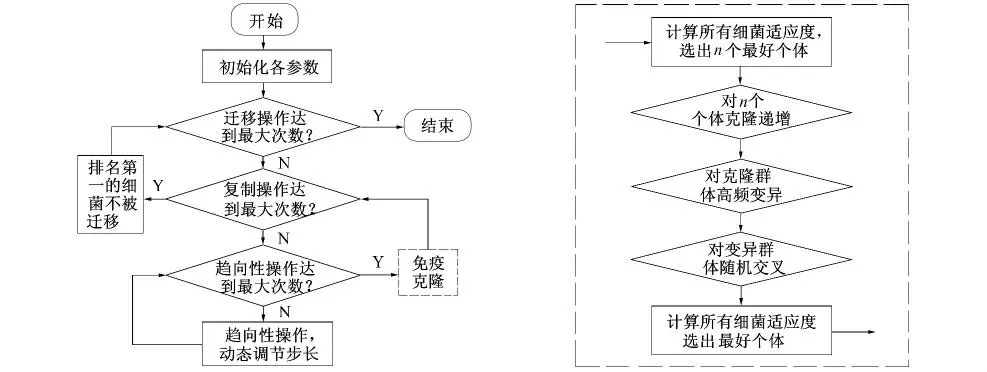
图1 GFBA算法操作步骤
4 实验仿真
4.1 拓扑模型
研究该类模型时,其拓扑图所含的n个节点都能通过对应的几率可通过下面的式子进行求解:
(1)
式(1)中,l(p,q)为网络拓扑图中两点间的欧式距离;L为网络拓扑图最大的边长;α,β为大于零小于1的两个实数:控制网络拓扑图中的边的数量,控制网络拓扑图中的短链路的数量。其对应的区域范围大小是200×200,50个节点和100个节点网络拓扑图,具体如图2、图3所示。
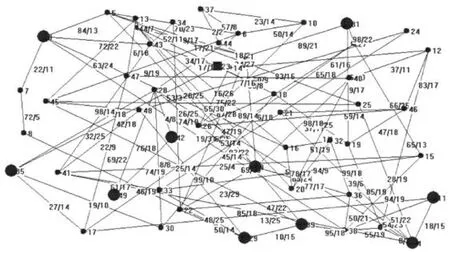
图2 50节点网络拓扑图
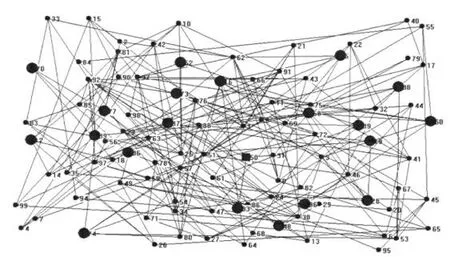
图3 100节点网络拓扑图
图2,3中方形节点为组播源,圆形节点为组播。
4.2 GFBA仿真结果
对于上面所得的拓扑模型,可利用GFBA算法求解计算,如图4和图5所示,黑色粗线为组播转发树。
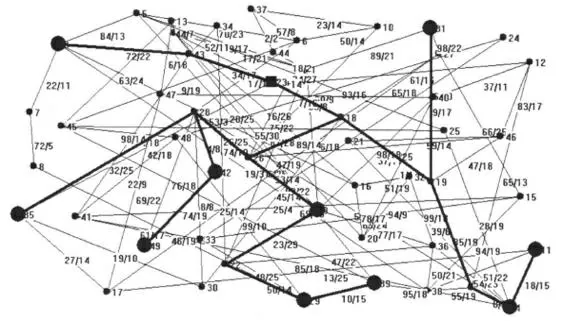
图4 50节点网络拓扑图计算结果
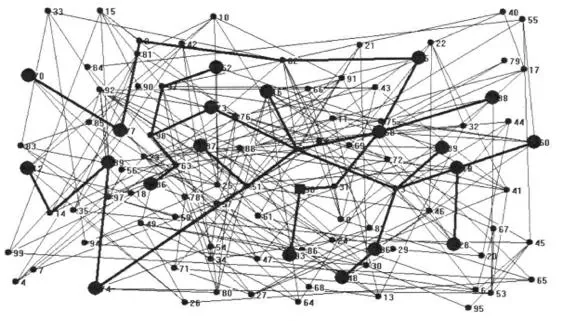
图5 100节点网络拓扑图计算结果
4.3 结果分析
针对GFBA算法里细菌个数、组播树费用值存在的关联性进行分析,可基于各个数细菌来求解50个、100个节点随机网络拓扑模型,最终结果则为得到的数据均值,具体如图6所示。
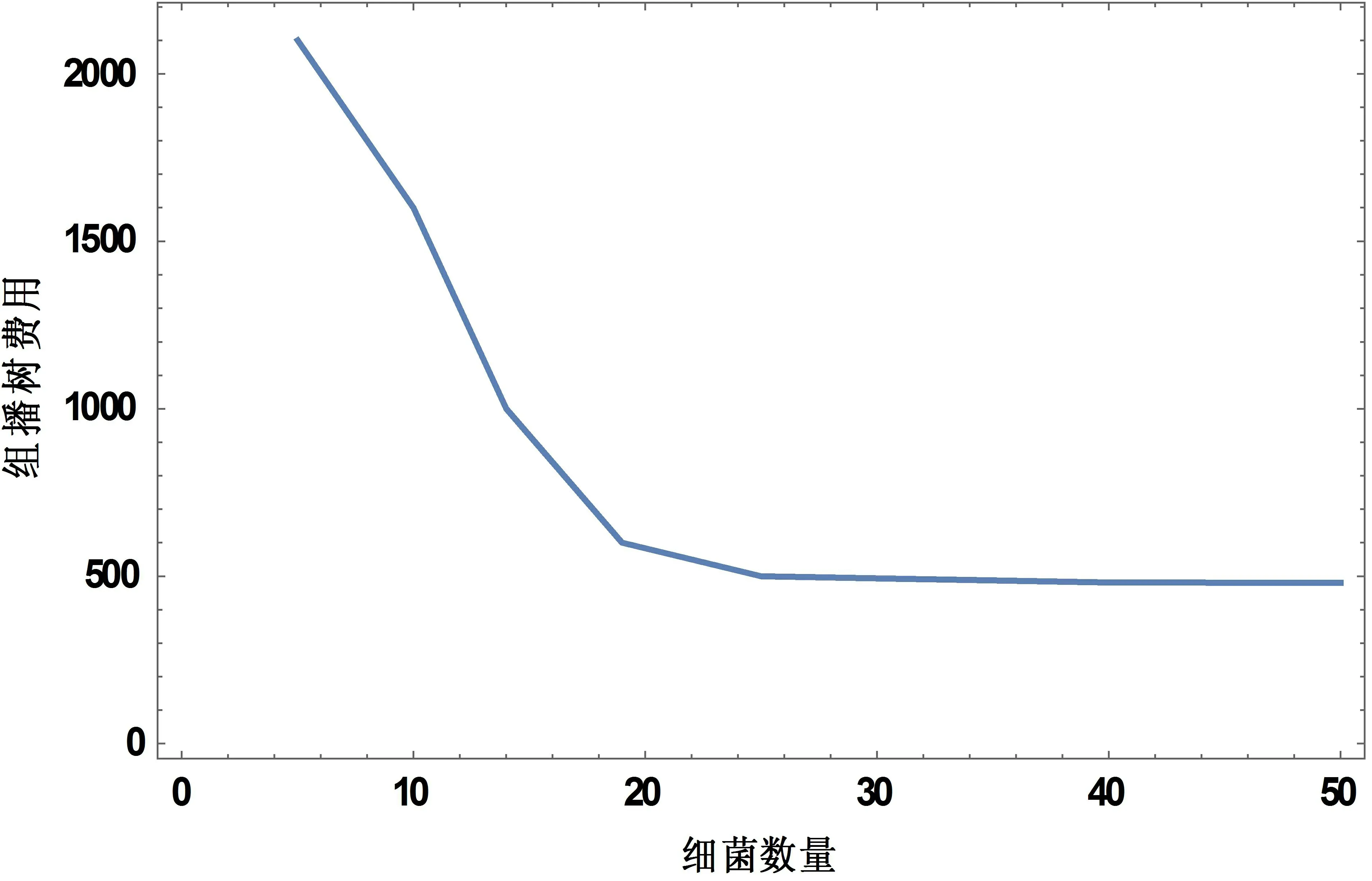
图6 细菌的数量和组播树费用值的关系
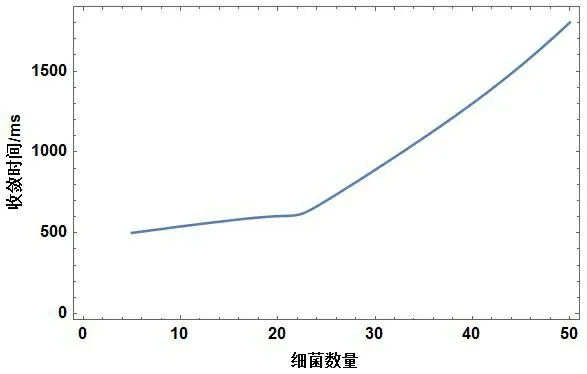
图7 细菌的数量和收敛时间的关系
如图6所示,当细菌个数小于19的时候,细菌数量的增加可以大幅度降低组播树费用,说明在这一阶段,由于细菌较少,GFBA算法对应的解也较少,其搜素最优解的范围很小,容易遗漏较小的值。当细菌个数大于19的时候,细菌数量的增加不可以大幅度降低组播树费用,说明在这一阶段,由于细菌已然足够,GFBA算法对应的解也较多,其搜索最优解的范围很广,容易找到最小的值。组播树费用、细菌个数见的关联性,以下面的数值来表达:
c=3999.387-486.792m+28.268m2-
0.656m3+0.002m4-0.000001m6+
0.00012m5-322.52cosm
(2)
式(2)中 ,c为组播树费用;m为细菌个数。
为探究GFBA算法中,细菌的数量和收敛时长见存在的关联性,通过各规模的细菌个数,求解50个、100个节点随机网络拓扑模型,最终结果则为得到的数据均值,具体如图7所示。
根据图6,7来看,细菌不足23个的情况下,其数量越多,那么收敛时长受到的影响较小,说明在这一阶段,由于细菌较少,GFBA算法的计算量也较小,容易找到所处情形下的最优解。当细菌个数大于23的时候,细菌数量的增加大幅度增加了收敛时间,说明在这一阶段,由于细菌数目增加,GFBA算法对应的解也较多,其搜素最优解的范围很广,收敛难度也增加。组播树费用和细菌数量的关联性可以表示成式(3):
t=-3576.263027036935-
734.2037534473963cosm+
20.4207599922332cotm+
1424.4592856578956lnm+
566.7544407805706secm
(3)
式(3)中,t为收敛时间(ms);m为细菌个数。
为对GFBA算法性能进行分析,了解其优势、适用性,也就是证明以下图示内容的正确性,可通过不同的算法来求解拓扑模型费用、收敛时长,也就是得到下面的图示结果,所应用的算法包括了遗传算法计、免疫克隆算法等。
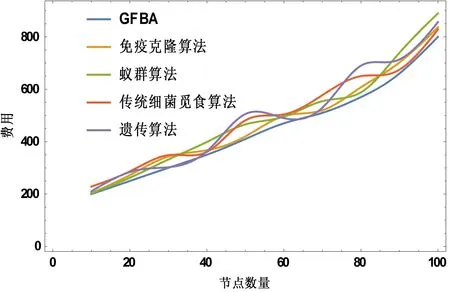
图8 不同算法节点数量和费用值的关系
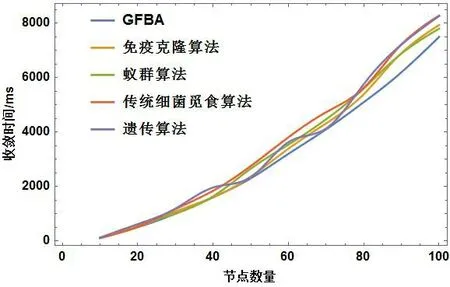
图9 各算法节点个数、收敛时长关联性
如图8所示,细菌数量越多,则费用也相对更高,本文利用GFBA算法得到的结果整体成本在随着节点数目增加的过程中,总体上要比其他算法计算得到的结果更低,说明提出的GFBA算法的全局搜索能力和收敛精度都高于免疫克隆算法、蚁群算法、传统细菌觅食算法、遗传算法。整体而言,算法提出的GFBA计算而得的费用要比其他算法更低,和免疫克隆算法、蚁群算法、传统细菌觅食算法、遗传算法比较来看,下降了5.78054%,8.49318%,10.6%,9.10569%。
如图9所示,细菌数量越多,收敛的时间也就越长,并且增大的幅度越来越大,利用GFBA算法整体时间成本随着节点数目增加的过程中,要比免疫克隆算法、蚁群算法、传统细菌觅食算法、遗传算法计算而得的收敛时间更短,说明提出的GFBA算法的计算效率高。综上所述,提出的GFBA算法计算而得的收敛时间和免疫克隆算法相比,减小了5.82%;和蚁群算法相比,减小了9.02%;和传统细菌觅食算法相比,减小了14.06%;和遗传算法求解而得的收敛时间低了14.12%。
5 结 语
针对在智能家居系统网络研究中,提出一种网络节点路由GFBA算法,该算法。在BFA、融合免疫算法(Generate and Test)基础上,又融合了半解析解的相关思想。并针对50节点和100节点的随机网络拓扑模型进行计算,验证GFBA的收敛能力。此外,通过对50网络节点和100网络节点的随机网络拓扑模型进行计算而得的收敛时间和费用进行研究,发现细菌的数量,在不足19的情况下,GFBA所得解数量相对少,覆盖面不全。反之,只要细菌数量达到一定量,那么这个算法所得解也相对多,覆盖面更广。最后,提出的GFBA算法的计算效率明显高于免疫克隆算法、蚁群算法、传统细菌觅食算法、遗传算法。相比较,费用比免疫克隆算法、蚁群算法、传统细菌觅食算法、遗传算法减小了5.781%,8.493%,10.6%,9.106%,收敛时长要比其他算法更短,对比免疫克隆算法、蚁群算法、传统细菌觅食算法、遗传算法,减小了5.815%,9.016%,14.058%,14.123%。

