斑马鱼C 型机动运动数据重构与性能分析

刘元森，余永亮，鲍麟，高梦忱

中国科学院大学 生物运动力学实验室，北京 100049

0 引 言

鱼类机动运动通常指鱼体在短时间内运动状态发生明显改变[1]，如起动、制动、转弯等。为了生存，在鱼体捕获猎物、逃避敌害、迁徙繁衍、沟通交流等行为中包含大量机动运动[2]。以身体和尾鳍做波状驱动的鱼类（如鲹科模式和鳗鲡模式），机动运动以C 型机动运动最为常见[3-4]。C 型机动运动由运动的准备阶段弯曲成“C”形而得名，包括C 型起动（Cstart）和C 型转弯（C-turn）。C 型起动持续时间较短（ 100 ms以内[4]），在转弯之后有明显鱼体反向弯曲的特征，常出现在鱼体逃逸行为中；而C 型转弯持续时间较长，鱼体在身体弯曲成C 形后逐渐伸直，不存在鱼尾反向弯曲过程[5]，主要帮助鱼体改变运动方向。

早期人们对鱼类机动运动的研究手段主要是定性观察实验[6]；Weihs[7]为了进行水动力分析，采用手绘的方式给出了鱼体的摆动和运动轨迹。此类方法定性地给出了机动运动的主要特征，促进了人们对鱼类机动运动的认识。步入21 世纪后，一方面实验仪器精度不断提高，鱼类活体实验逐步从定性观察向定量分析过度，高速摄像技术不断向更高时空分辨率、更低检测限与畸变程度发展，现已基本满足生物运动研究所需[8]；另一方面，数字图像处理技术（digital image processing）的诞生与快速发展，显著提高了数据的获取精度与效率。Bang等[9]首次基于图像处理技术完成了鱼体整体平动的追踪，但其追踪对象仅为鱼体上的特定点，而非质心。Tytell 和Lauder[10]采用半自动方法捕获了鱼体机动运动的中轴线和轮廓信息，虽然精度较高，但需要人工来识别每幅图像中鱼体头部尖端和尾鳍末端的位置。随着人们对图形学研究的深入，发展了直接从图像中提取鱼体骨骼线的数学形态学算法[11-13]，此方法鲁棒性虽好，但对鱼鳍的识别存在较大误差，从而影响鱼体运动学和动力学的分析。

为了克服图像中形状各异的鱼鳍对形态学提取造成的干扰，Fontaine 等[14]首次用建立标准几何模型的方式，对图像中的识别错误进行了有效的检验和修正。由于他们所用鱼体标准模型的形状不包含鱼鳍，导致在鱼体机动运动分析中完全忽略了鱼鳍（特别是尾鳍）的动力学贡献。然而，在鱼体机动运动的形态学重构中，鱼鳍的识别和重构是主要难点[15-16]。如何将图像中的鱼鳍通过合理的建模等效，纳入鱼体标准模型中，依然是一个悬而未决的问题。

斑马鱼易于获得和饲养，C 型机动运动特征明显，故本文将其作为实验对象。首先搭建基于机器视觉的高速摄影平台，获取顶视的序列图像；然后使用数学形态学算法提取图像中的鱼体外轮廓和中线，对尾鳍进行动力学等效建立简化三维模型；最后通过“鱼–水”系统的动量和动量矩守恒，获得鱼体的运动学数据，分析作用于鱼体的流体动力和机械能的变化规律。

1 平台搭建与测量

1.1 材料的准备与平台搭建

选取10 尾成年斑马鱼，在室温（20～25 ℃）鱼缸中集群饲养。设置昼夜各12 小时循环的光周期环境，每日上午9:00 对斑马鱼进行饵料饲喂。实验鱼体长度L=3.91±0.14 cm， 质量m=0.74±0.09 g。

为了获得拍摄视场亮度均匀稳定、鱼体与背景环境对比度高的图像，在张冰冰等[17]的研究基础上进行改进，搭建了采用直流LED 作为光源的高速摄像实验平台，如图1 所示。

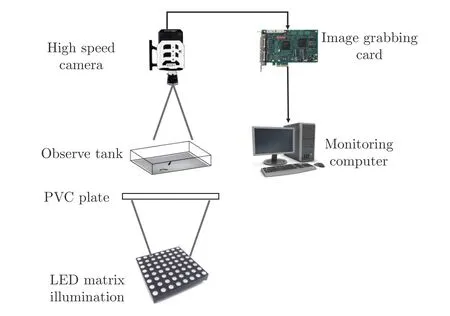
图1 斑马鱼动作捕获实验平台示意图Fig. 1 Sketch map of experimental platform for zebrafish swimming

实验时，在20 cm（长） × 20 cm（宽） × 5 cm（高）的水槽中加入饮用矿泉水，放置成年斑马鱼1 条。为防止鱼体运动时水体自由面变形，在实验中将玻璃板（厚2 mm）紧贴水体上方放置，四周留有空隙以交换空气。实验前，先将斑马鱼放置于水槽中2 h 以适应环境。实验时，使用声刺激诱使斑马鱼逃逸。

在水槽正上方约1 m 处放置高速摄像机（分辨率1080 像素 × 800 像素，比例尺约 6 135像素/m，镜头焦距 80 mm）拍摄鱼体的机动运动，拍摄频率500 Hz。

优质图像是获取高精度运动学数据的前提和保障，机器视觉领域[18-19]对其提出如下要求：1）目标与背景的边界清晰，图像对比度高；2）背景应尽量淡化且亮度均匀稳定，不对图像处理造成干扰；3）色彩真实，既保证视场明亮，又不能曝光过度。为满足以上要求，本文用直流LED 阵列（ 30×30）进行明场照明，在光源和水槽之间放置0.5 cm 厚的PVC 板以降低光强的集中度，使得光源具有高亮度、低穿透特性。

1.2 拍摄效果

图2 为拍摄得到的斑马鱼C 型起动序列图像，其中图2（f）中红色曲线为质心运动轨迹，圆点为各个特征动作时质心所处位置。经检验，图像中最大畸变误差为2 像素，相对误差 0.835%。多次实验时，视场的光照强度I 稳定在 1 225±168 Lux，拍摄图像的背景环境灰度稳定在 170±30（整型8 位灰度图），而图像中的鱼体躯干灰度在60 以下，鱼鳍灰度在60～130之间。鱼体躯干、鱼鳍和背景环境间存在差异性。

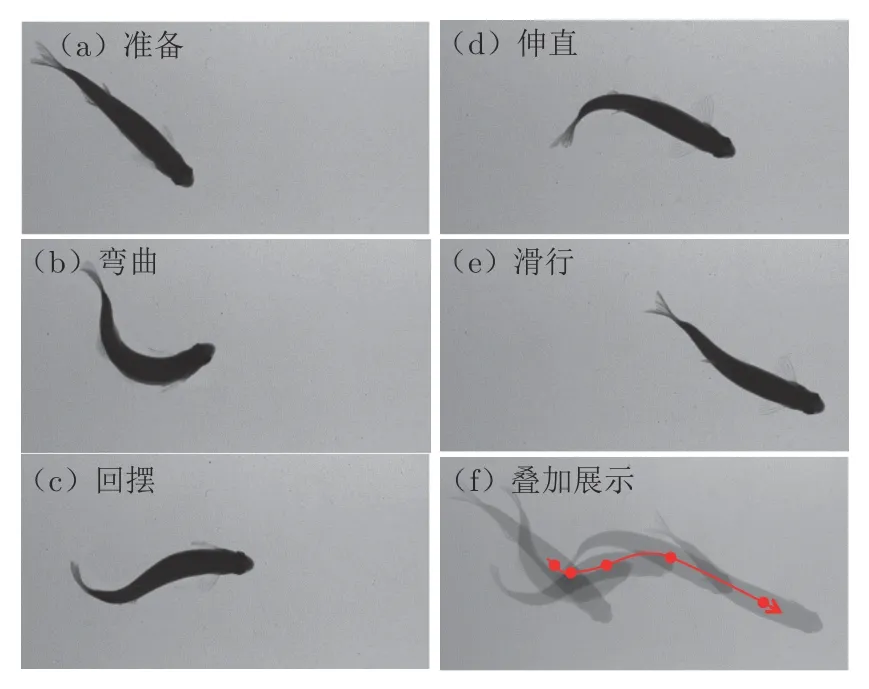
图2 C 型起动过程中典型动作的拍摄效果Fig. 2 Typical images of a C-start motion

基于机器视觉搭建的明场、背光、漫反射顶视高速摄像平台，可获取斑马鱼机动运动的高对比度优质序列图像，背景简单稳定，鱼体形态学信息清晰且易于提取。

2 图像处理与误差

2.1 问题分析

数字图像中包含的鱼体形态学信息主要为鱼体的中轴曲线、鱼体的边界轮廓和鱼鳍，其中鱼鳍又可以细分为胸鳍、背鳍、腹鳍、臀鳍和尾鳍。鱼体躯干与背景环境对比度较高，故中轴线提取难度较低。而鱼鳍与躯干的灰度范围存在重叠，将会影响鱼体轮廓的提取。且在鱼体机动运动过程中，鱼鳍往往具有姿态复杂的形状特性，难以对其进行有效识别。

图3 为斑马鱼多个C 型起动中不同阶段的数字图像和二值图像，红色虚线包围区域所示的鱼鳍将对轮廓识别带来干扰。特别是对推进起重要作用的尾鳍，在识别中会部分丢失或呈现出三维特性，如剪刀形、矩形和扇形等。因此，在鱼体机动运动序列图像的形态学特征识别中，鱼鳍的识别是主要难点。

图3 鱼体机动运动中弯曲、回摆和滑行阶段代表性动作与其二值化效果Fig. 3 Typical images and their binarization identification of the fish body and fins during bending, swinging back and coasting motions

2.2 形态学数据获取

本文使用OpenCV 数字图像处理库函数对拍摄的图像进行预处理、形态学特征提取和运动学特征提取，完成运动数据的捕获。

首先，对存在背景噪声的灰度图像（图4（a））进行预处理：使用差分算法识别图像中鱼体机动运动的范围[20]；使用3 × 3 均值滤波器对图像的灰度进行局部平均，以增强鱼体躯干、鱼鳍与背景环境3 者的灰度差异（图4（b））；将原8 位灰度图像进行二值化（图4（c）），其中二值化阈值为整幅图像平均灰度的80%（图像的平均灰度为165～190，故二值化的阈值取132～152）。在二值图像中，鱼体为面积最大的连通域，其余为噪声。

图4 形态学数据提取步骤Fig. 4 Flowchart of digital image processing for zebrafish swimming

然后，对于鱼体进行形态学（鱼体中轴线和外轮廓信息）提取，主要使用数学形态学算法：对二值图像从直接用边缘检测函数（edge）初步得到鱼体轮廓（图4（f））；对图像中的鱼体，重复使用细化（thin）操作从鱼体的外围逐层剥削像素，得到图像中仅存在单个像素宽度的笔画（图4（d）），它包含了鱼体的中轴线信息；对图像中的鱼体使用骨骼化（skeleton）操作，将视场中的鱼体视作多边形，沿轮廓检测其顶点，并将识别的顶点连接，生成鱼体的骨骼线（图4（e））。由于细化得到的曲线并不完整，骨骼化得到的曲线并不精确，故本文将骨骼曲线的首尾两段拼接于细化曲线之上，再经过毛刺剔除和曲率优化，从而获得精确的中轴线信息（图4（g））。

最后，使用获取的中轴线剔除轮廓曲线中的尾鳍识别误差，就得到了精确的鱼体轮廓信息（图4（h））。

在不同组实验中，图像灰度和噪声存在差异，使用统一的阈值参数处理难以得到理想的效果。为了充分考虑实验环境差异与鱼体的个体差异，提高数据处理精度，引入包含鱼体躯干与鱼鳍信息的标准模型修正鱼体轮廓和尾鳍长度。

在建立鱼体标准模型时，假设鱼体的横截面形状为椭圆，则可通过鱼体的主视图和俯视图（图5（a）、（b））获得椭圆截面的长轴 2a(s)和短轴 2b(s)随体长的分布（s 含义见后文）。从舒展状态的主视图（图5（c））中获取鱼鳍的相对位置，实验测得胸鳍、腹鳍、背鳍、臀鳍和尾鳍大致处于鱼体长度的0.18、0.38、0.5、0.54 和0.84 处。经验证，仅保留鱼体躯干和尾鳍，并假设鱼体密度均匀（ρ= 1.00 g/cm3），则计算得到的鱼体质量与实验测得的鱼体质量误差小于3%。

机动运动中，胸鳍和腹鳍主要维持推进稳定，背鳍和臀鳍主要防止鱼体摆动时翻滚，而尾鳍对推进有重要贡献[21-23]。故在形态学数据提取时，将胸鳍、腹鳍、背鳍、臀鳍进行位置识别，并从躯干中抹去。主要考虑鱼的躯干与尾鳍，从而建立如图5（d）所示的鱼体标准模型。

图5 基于标准模型的鱼鳍识别与修正Fig. 5 Fins recognition and correction

对尾鳍的识别和等效是困难的。侧面为剪刀形的尾鳍在运动中由于流体作用而产生三维形变，从顶视拍摄的数字图像中，呈现出如图6（a）所示的4 种形貌。AB 为尾鳍始端，即尾柄宽度；JK 为末端，出现薄片形、扇形、剪刀形和刀形。在标准模型中，对尾鳍的等效有两部分：一是通过几何对称性给出等效的尾鳍中线，即图6（a）中OE；二是通过尾鳍面积二阶矩的动力学等效原理来确定的尾鳍长度，即把剪刀形的尾鳍等效为等腰梯形，如图6（c）所示。

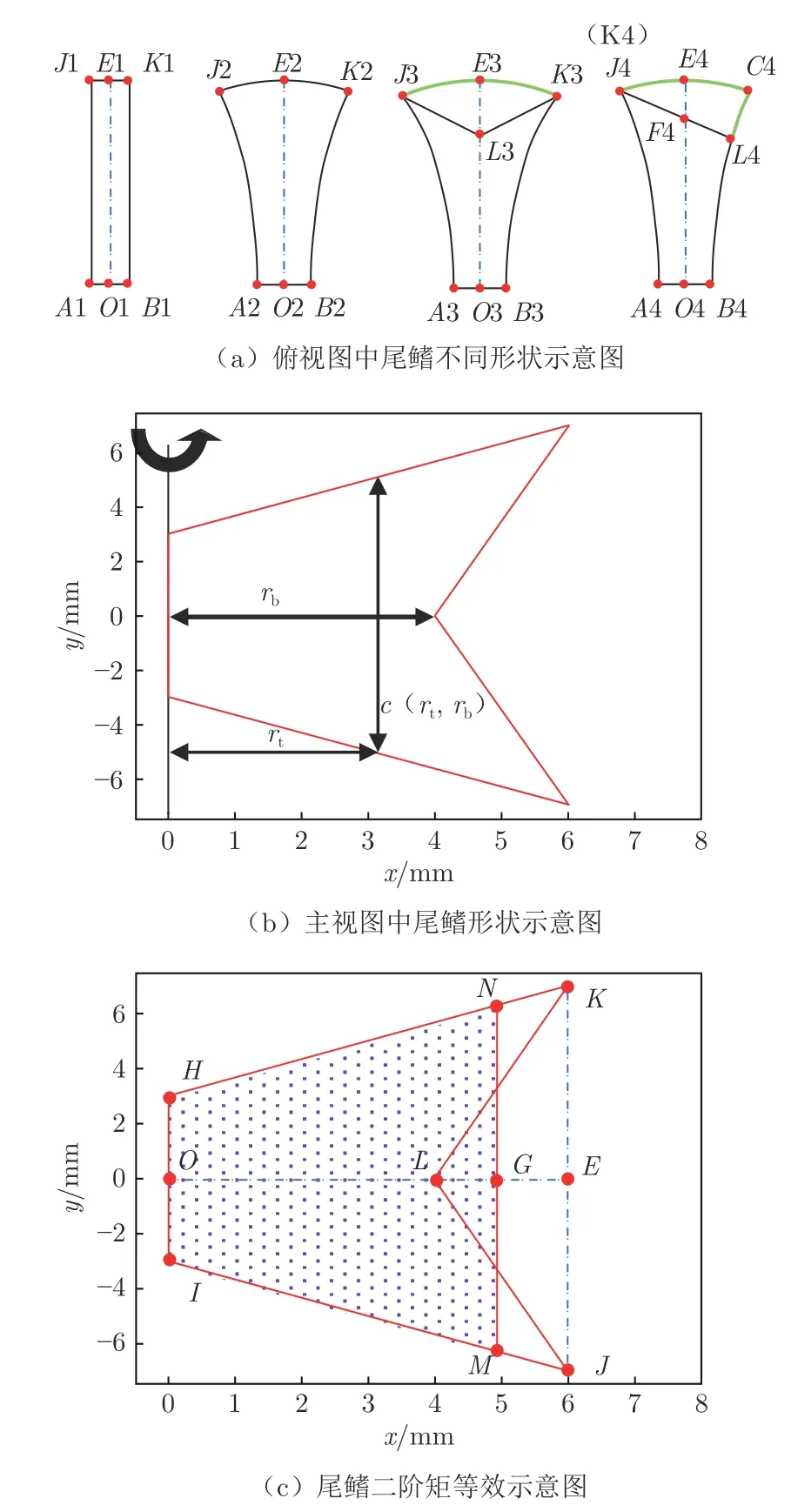
图6 尾鳍的位置识别与长度确定Fig. 6 Determination of position and length of caudal fin

Weis-Fogh[24]发现不同形状的翼拍动时，平均升力与翼型面积的二阶矩成正比，因此，可以用二阶矩等效消除不同个体尾鳍的剪刀形差异。剪刀形尾鳍HIJLK（original shape）与等效梯形尾鳍HIMN（equivalent shape）的面积二阶矩由公式（1）给出：

式中：S2os为剪刀形尾鳍的面积二阶距，S2es为等效梯形尾鳍的面积二阶距；rt为尾柄到尾鳍末端的距离，rb为尾柄到剪刀形尾鳍分叉点的距离（图6（b））；c(rt,rb)和c(rt)分别为对应位置的剪刀形尾鳍有效宽度和矩形尾鳍宽度。通过S2os=S2es解出等效鱼鳍长度OG。经过位置与长度等效，任意复杂形状的尾鳍皆可转化为动力学效应相等的等腰梯形。实验中所测斑马鱼尾鳍的等效长度OG=0.79±0.13OE。

2.3 运动学和动力学数据获取

鱼体的C 型机动包含平动与转动，平动可以通过质心的位移进行计算，转动则需通过“鱼–水”系统的动量矩守恒来求解。基于2.2 节工作中提取的形态学数据，将鱼体横截面假设为椭圆，可重构出三维鱼体，如图7 所示。鱼体上任意一点P 的运动可以分解为质心平动、绕质心转动和变形运动，3 者存在如下关系：

图7 鱼体的三维重构示意图（左）及惯性系与质心系间关系（右）Fig. 7 Sketch map of fish 3D reconstruction model Relationship between inertial system and centroid system in maneuvering motion

在图7中，Oxy为实验室坐标系，Cx′y′为鱼体质心坐标系。其中C为鱼体质心，为质心在实验室坐标系下的位置矢量，为P 点在实验室坐标系下的位置矢量，为P 点在质心坐标系下的位置矢量，s为鱼体中轴线从头至尾的自然坐标。鱼体的整体平动信息包含质心位置、平动速度、平动加速度和所受合力，依据三维的鱼体模型计算：

式中：ρ为鱼体的密度，V为鱼体体积，m为鱼体总质量，t 为时间。转动信息的求解则是依据“鱼–水”系统动量矩守恒[25]。鱼体在转动时，纯变形运动满足动量矩守恒，如式（4）所示。结合式（2）即可求得鱼体绕质心转动的角速度，如式（5）所示。然后，通过对时间的积分和微分求得整体转动的角度（转角）和角速度（式（6））。最后，通过式（7）求得鱼体所受弯矩之和，其中为鱼体在质心坐标系下的转动惯量。

在以上运动学和动力学数据的计算中，涉及对时间的求导运算，这将导致截断误差不断放大，如图8 中蓝色虚线所示。为降低误差随求导次数的累积，采用最小二乘平滑滤波（savitzky-golay filtering）方法对质心位置变化和转动速度数据进行滤波，有效地保留数据的真值。

图8 S−G 滤波对运动学数据捕获的优化效果Fig. 8 Effect of S−G filtering on kinematics data acquisition

2.4 误差与验证

本文实验误差主要由截断误差和系统误差两部分组成，而系统误差又可细分为图像畸变误差和处理算法误差。截断误差取1 像素，相对误差为0.417%（1080 像素 × 800 像素，比例尺约 6 135 像素/m，则绝对误差0.0163 cm），畸变误差实测不超过2 像素（绝对误差 0.835%）。

而对于图像处理的总误差，可通过标准算例进行验证。如表1 所示，分别设置NACA0010 翼型做匀速直线、匀加速直线、匀速圆周、匀加速圆周和波状摆动运动。考虑两种图像分辨率下，质心位置、速度、加速度、角速度和角加速度的最大误差。在直线运动中，为鱼体质心的平均运动速度；圆周运动中，鱼体以角速度ωC(t)绕头部转动；波状摆动运动中，质心的平均速度，y(s,t)为鱼体摆动时的侧向位移。设置比例尺和“拍摄”频率与实验相同，翼型长度为 4 cm， 运动持续时间为 0.2 s。对序列图像进行处理，将计算所得运动学数据与理论真值比较，获得相对误差（relative error, ER）。

表1 标准算例参数设置与运动学数据相对误差Table 1 Parameter setting of standard example and kinematic data error

结果表明，质心位置识别的最大相对误差为0.41%，速度和加速度的最大相对误差分别为1.23%和3.07%。并且，在不改变其他条件、仅提高图像分辨率情况下，数据的相对误差会随截断误差的减小而减小。

3 实验结果与分析

3.1 单次运动分析

前人对C 型机动运动进行运动阶段划分时，是依据头部角速度ωh的两个零点，将机动运动划分为准备（Stage 1）、加速推进（Stage 2）和滑行（Stage 3）3 个阶段[3,11]。本文主要研究前两个阶段的动力学特征。在准备阶段，鱼体在短时间内弯曲成“C”形，在加速推进阶段，鱼体通过回摆与水体相互作用实现推进。当鱼体无明显反向回摆动作时，规定鱼体达到伸直状态即为加速推进阶段结束。

图9 为斑马鱼一次典型C 型起动的整体平转动数据，包括质心运动速率uC与加速度aC、头部转动角度φh与角速度ωh、质心系转动角度φC与角速度ωC、质心系角加速度βC与力矩MC。对于该C 型机动运动，两阶段持续时间不超过 60 ms，符合张冰冰等[17]对C 型起动的观察结果。这说明斑马鱼在短时间内运动状态发生明显变化，以满足逃逸或捕食需要。

图9 一次C 型起动中鱼体各运动学数据随时间的变化Fig. 9 Kinematics vary over time in a fish C-start motion

鱼体在准备阶段（Stage 1），aC达到峰值（图9（a）），说明在该阶段鱼体与流体发生了强烈的相互作用。而且，头部的转动总是先于质心系的转动，转动幅度也大于质心系（图9（b）和（c））。在推进阶段（Stage 2），由于反向力矩作用，鱼体的转动角速度ωC减小，但转动的角度φC持续增大，直到在推进阶段中期达到最大转动角度（图9（c））。在此后推进阶段，鱼体反向转动，头部转角减小。

从图9（d）可见，在整个C 型起动过程中，鱼体所受合力矩MC与角加速度βC的走势基本一致，说明机动运动中鱼体转动惯量JC变化较小。但是，对比图9（b）与（d）不难发现，以运动学或动力学数据的零点作为运动阶段划分的依据，则结果并不重合。如果使用动力学特征来划分第一阶段，得到的结果将比运动学划分早 5～7 ms。

鱼体机动运动是一个动力学过程：由鱼体内部的肌肉收缩使得鱼体弯曲，进而通过鱼体与水体相互作用实现推进。在这一过程中，本应充分考虑动力学量来进行运动阶段划分，但考虑到观测的困难性和过程本身涉及复杂动力学响应[26]，采用头部转动角速度对C 型机动运动进行阶段划分仍是合理有效的。

此外，图9（c）表明，在滑行阶段虽然头部转动已经停止，但是质心系的转动仍在继续，直到起动后100 ms （图中 120 ms），鱼体才达到真正的滑行状态。

3.2 运动中的能量转化关系

从能量转化与守恒的角度看，鱼体在C 型机动运动中通过侧向摆动的方式将肌肉所做机械功传递到“鱼–水”系统，其中一部分转化为鱼体动能，另一部分转化为流体动能与耗散热。Wang 等[27-28]对鱼体机动运动过程中的能量分布进行分析，发现类似于式（2）的运动分解，鱼体的机械能Eb也可以分解为3 部分：平动能EC、 转动能Eω和变形能Ebd，如式（8）所示：

首先，选取转角为 31.0°的C型起动和109.3°的C 型转动进行对比分析，如图10（a）和（b）所示。对于C 型起动（图10（a）），其转动能在准备阶段存在峰值，但其增长的速率远小于平动能；平动能在准备阶段和加速推进阶段持续增大，直到接近加速推进阶段尾声才达到极大值；变形能在整个机动过程中相对都很小。这说明C 型机动运动的大部分机械能是为了平动推进，而转动占比小。

图10 鱼体 C 型机动运动中机械能及其分量随时间的变化Fig. 10 Variation of mechanical energy and its components with time in zebrafish C-shaped maneuvering

对于C 型转弯（图10（b）），转动能在准备阶段中占比高，而在加速推进阶段占比小；平动能在准备阶段的中期达到极值，随后变化较小；变形能在准备阶段的早期达到极大值，随后迅速下降到较小的值。这与C 型转弯在第一阶段完成整体转弯的运动学规律一致，在第二阶段，该运动仅在维持原有运动方向的基础上将身体伸直。对比发现，由于目的不同，斑马鱼的C 型起动与C 型转弯动作中，机械能的分配存在差异。

然后，选取转角为 6 6.5°和 1 64.0°的C 型转弯进行对比，如图10（c）和（d）所示。随着总转角φC的增大，C 型转弯的转动能Eω占总机械能Eb比例进一步增大，图10（d）中转动能峰值达到了总机械能峰值的81.56%。且不难发现，两个动作在推进阶段（Stage 2）都出现了平动能的增加，这是鱼尾回摆动作导致的推进现象。在C 型转弯运动中，较大幅度的鱼尾回摆会缩减加速推进阶段的持续时间，并促进转动能向平动能转化。

除平转动能分布随时间变化以外，变形能也具有独特规律。首先不论C 型转弯还是C 型起动，变形能曲线呈双峰形状，能量的峰值恰与鱼体弯曲和回摆两个特征动作对应。两峰值间存在一个低谷，此时鱼体几乎不变形，整个身体在弯曲成C 形后借助惯性做刚体式运动。由于C 型转弯主要依靠弯曲动作做功，回摆动作微弱，故变形能的谷值时刻恰为总机械能的峰值时刻。此后，鱼体的机械能逐渐耗散到流体中。

3.3 机动运动统计分析

为进行斑马鱼机动运动规律的统计分析，本文处理了160 组斑马鱼机动运动实验数据，包含C 型转弯、C 型起动和少量S 型起动，皆为斑马鱼在声源刺激下做出的机动响应。

用斑马鱼机动运动准备阶段和加速推进阶段的质心平均速度来定义雷诺数，即，其中为两阶段的平均速度大小，ν为运动黏度，查表可得ν=10−6m2/s。统计表明，雷诺数主要分布在1000～8000 范围，其频次占总数的88.1%，如图11（a）所示。强机动运动的占比较低，但雷诺数最大可达30000。图11（b）给出了不同转角（从机动运动开始到推进阶段末的总转角）出现的频次，可看出机动运动在30°和100°附近出现两个峰值。更小角度（< 20°）的C 型机动运动其姿态与S 型起动相近；而更大角度（> 150°）的C 型转弯持续时间较长，存在一个鱼体弯曲之后依靠惯性滑行的状态。

图11 斑马鱼C 型机动运动统计规律分析Fig. 11 Statistical analysis of zebrafish C-shaped maneuvering

此外，图12 （a）和（b）分别统计了机动运动中质心最大加速度aC,max与质心最大速度uC,max和质心最大角加速度βC,max的关系。结果表明，uC,max与aC,max存在二次曲线相关，aC,max与βC,max呈线性相关（R2=0.966）。

无论是C 型起动还是C 型转动，都存在平动和转动，前者主要为了获得更大的起动速度，后者是为了获得更大的转弯角度。总之，更剧烈的转动带来更强的平动，统计结果正好体现了这类机动运动的单调性特征。故图12（b）中最上方数据反映了斑马鱼机动运动中鱼体所受力矩极限（约 0.12 mN·m），最右方数据反映了鱼体所受合力极限（约 32 mN）。

图12 C 型机动过程中运动学数据的相关性Fig. 12 The relationship between kinematic parameters

3.4 结 论

本文搭建了基于机器视觉的高速摄像平台，捕获了具有背景简单稳定、鱼体形态学信息清晰特点的斑马鱼C 型机动运动的序列图像；使用数字图像处理技术获取了鱼体轮廓和中线并建立了简化的三维鱼体模型；利用变形体动力学与力能学分析手段，对机动运动中的运动学、动力学和机械能等信息进行分析。主要结论如下：

1） 使用椭圆横截面假设，建立了基于顶视投影图像的鱼体三维模型。其中，对尾鳍使用动力学二阶矩等效，消除了鱼尾的三维形态差异，并合理修正了其长度。

2） 两种C 型机动运动在做功中存在差异。C 型起动在准备阶段和加速推进阶段均不断加速，从而获得了较大的速度，其平动能远高于转动能；C 型转弯的转动能在准备阶段远高于平动能，在加速推进阶段，转动减弱，平动速度得以维持或小量增加。

3） 无论是C 型起动还是C 型转弯，最大加速度与最大速度间存在二次曲线关系，最大角加速度和最大加速度之间存在线性关系，更剧烈的转动会带来更强的平动。

C 型起动是为了短时间内获得较大平动速度，C 型转弯是为了短时间内获得较大转动角度。两者的特征在运动学、动力学和力能学方面既存在差异，又存在统计意义上的相关。