基于电网谐波阻抗估计的并联电容器组优化配置方案
甘景福 李昕朔 王月 李永刚 潘建铭 李爱民 周磊


摘 要:采用先投入高串抗率電容器、后投入低串抗率电容器这种单一配置方案,导致变电站出现高串率电容器频繁投切、寿命降低和无功容量浪费问题。为了解决这些问题,提出一种基于阻抗估计和多电能质量约束的变电站电容器组优化配置方法。首先,获取电容器投切后公共连接点母线电压电流数据;其次采用小波最大最小阈值去噪,通过Prony算法得到暂态电压、电流数据来估计系统谐波阻抗,最后结合AVC下达的调度指令和目标函数在满足电网电能质量约束条件下对电容器组进行优化配置。结果表明,在满足电能质量约束和AVC调度指令下,优化配置后高低串抗率配置频次均有所改善,高串抗率电容器组投入频次下降32%,低串抗率电容器组投入频次由26%提高至58%。由系统谐波数据、谐波源和电容器等元件组成的谐波阻抗模型,以及基于谐波谐振机理设计的电容器组配置方案,能够提高数据分析的准确性,减小电容器损坏以及解决无功容量损失问题,提高供电质量,可为变电站电容器组的配置提供借鉴。
关键词:电力系统及其自动化;变电站电容器组配置;多串抗率选择;谐波阻抗估计;小波去噪;电能质量标准
中图分类号:TM743
文献标识码:A
DOI: 10.7535/hbgykj.2023yx02004
Optimal configuration of parallel capacitor banks based on grid harmonic impedance estimation
GAN Jingfu1,LI Xinshuo2,WANG Yue3,LI Yonggang2,PAN Jianming2,LI Aimin1,ZHOU Lei1
(1.China Tangshan Power Supply Company, State Grid Jibei Electric Power Company Limited, Tangshan, Hebei 063000, China; 2.School of Electrical and Electronical Engineering, North China Electric Power University, Baoding, Hebei 071003, China; 3.Nantong Power Supply Subsidiary Company, State Grid Jiangsu Electric Power Supply Company Limited, Nantong, Jiangsu 226006, China)
Abstract:In order to improve the problems of frequent switching, lifetime reduction and reactive power capacity waste of high-series capacitors caused by the single configuration scheme of putting in high-series capacitors first and low-series capacitors later in substations, an optimal configuration method of substation capacitor bank based on impedance estimation and multiple power quality constraints was proposed. Firstly, bus voltage and current data of common connection point was obtained after capacitor switching, the wavelet maximum-minimum threshold was used to denoise, the transient voltage and current data were obtained by Prony algorithm to estimate system harmonic impedance, and the configuration of capacitor banks under the grid power quality constraints was optimized, combining with the scheduling instructions from the AVC (automatic voltage control) and objective functions. The results show that, under the condition of satisfying the power quality constraints and AVC dispatching command, the frequency of both high and low series impedance configuration is improved after the optimized configuration, and the frequency of high series impedance capacitor bank input decreases by 32%, while the frequency of low series impedance capacitor bank input increases from 26% to 58%. The harmonic impedance model consisting of system harmonic data, harmonic sources and capacitors, and the capacitor bank configuration scheme designed by the harmonic resonance mechanism improves the accuracy of data analysis, reduces capacitor damage and reactive capacity loss, and improves the quality of power supply, which can provide reference for the configuration of substation capacitor banks.
Keywords:power system and its automation; substation capacitor bank configuration; multi-string resistance rate selection; harmonic impedance estimation; wavelet denoising; power quality standards
近年来,随着电力系统中电力电子设备的大规模使用,谐波源负荷急剧增长,产生大量谐波注入电网[1-2]。电力系统中装设并联电容器起到提高系统功率因数、改善电压质量等作用,但是电容器投入后会改变电网阻抗特性,对谐波呈放大作用,严重威胁系统的安全稳定运行。
目前主要采用将电容器配合特定串抗率电抗器使用的方法来解决谐波放大问题[3-4],陈柏富等[5]基于电网中各次谐波成分大小和谐波抑制原理进行串抗率选择。翟运娟等[6]对混装电容器组谐波电流放大原理进行了分析,但并未对多电抗率电容器组并联混装运行时的配置策略进行研究。根据现有研究[7-10],自动电压控制(automatic voltage control,AVC)系统为确保谐波不会过度放大会先投入高串抗率的电容器,这会使低串抗率电容器动作次数相比高串抗率的电容器少甚至基本不投入,而高串抗率电容器频繁投入,其寿命会大大缩短。
陈伯胜[11]指出谐波放大與系统谐波阻抗有关,但是其只是简单地通过基波阻抗乘以谐波次数的经验公式进行计算,这是不够准确的。郝福忠等[12]提出电容器串联电抗器电抗率需考虑电网背景谐波的影响。张程等[13]扩充无功规划适用范围且不局限于某一负荷水平,但是并未考虑高低串抗率电容器组之间的配合问题。本文通过电容器组投切计算谐波阻抗[14-15],阻抗的获取有助于准确判断电容器组是否满足投切要求,避免经验公式计算导致的偏差过大;以系统电能质量和电容器运行工况作为约束条件[16-17],通过采用遗传算法对目标函数寻优,最终得到的电容器组优化配置方案能够缓解高串抗率电容器组频繁投入带来的寿命损失和无功容量浪费的状况,提高设备运行的经济性。
1 并联电容器对谐波的影响分析
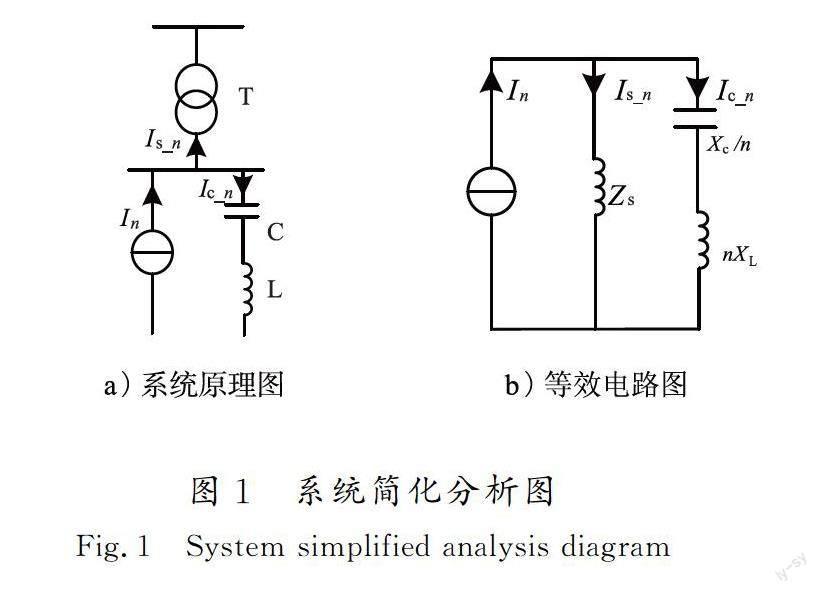
电力系统中非线性负荷构成谐波源向系统中注入谐波,电容器串接电抗器具有抑制谐波的作用,在电容器装置侧有谐波源时的等效电路模型见图1。
注入公共连接点的谐波电流分别流向系统侧和电容器支路,电容器支路和系统侧谐波电流如式(1)和式(2)所示。
式中:Is_n为系统侧谐波电流;Ic_n为电容器支路谐波电流;In为谐波源发出的谐波电流;Zs为系统谐波阻抗;XL,Xc为电容器基波感抗及容抗。
系统侧谐波电流的放大倍数Ks和电容器支路谐波电流的放大倍数Kc分别为式(3)和式(4):
式中:Ksc =Zs/j(XL-Xc)。
定义α=Xs/Xc为系统电抗比,n为谐波次数,电容器串抗率k为基频下感抗XL与容抗Xc的比值。谐波电流放大倍数与电容电抗率k、系统电抗比α以及谐波次数n之间的函数图如图2所示。从三维函数图可以直观看出,对于高次谐波,低电抗率的电容器有更高的谐波放大倍数;电抗率为6%时,对于4次及以下低次谐波会在系统电抗比为特定值时出现较高的放大,但对于高次谐波在各种情况下均有较好的抑制作用;电抗率为12%时,考虑系统电抗比在实际情况下不会趋于0,因此对于3次及以上谐波均有抑制作用。
2 基于电容器投切的谐波阻抗计算方法
2.1 暂态分量提取与谐波阻抗计算
图3为单相电路简化模型,Us为系统等效电压源Us=Asin(ωst+φs);A,ωs,φs分别是系统电源幅值、角频率和相角;Zs为系统侧阻抗,对应为Rs+jωLs;Zc为用户侧阻抗;I为系统侧电流;Uc为电容器两端的电压。以图3对电容器投切注入电网暂态电压推导。
电容器投入后Uc可分解为式(5)的2个部分,式中Ucs为稳态分量;Uct为暂态分量。
稳态分量Ucs如式(6)所示:
求暂态分量时先得到电容器未投入时刻电压Uc(0-),由于能量不能突变进而得到电容器端电压初始值Uc(0+)见式(7)。
暂态电压Uct表示为式(8):
结合式(5)、式(6)和式(8),可得式(9):
暂态电流分量It计算同上述分析过程。因为稳态分量是由Us和系统参数决定,为基波正弦量,因此需将Uc和I中基波分量滤除。即可得电容器组注入电网的任意频率下的电流和电流响应,根据式(10)计算谐波阻抗。
式中:ω0=2πf;Z(jω0)是关于频率f的公共连接点母线处的谐波阻抗,采用暂态分量而非全分量是为了避免稳态分量的频谱泄露。
本文采用Prony算法对信号Uc,I进行参数辨识,提取出稳态分量Ucs,Is,进而得到暂态分量Uct=Uc-Ucs,It=I-Is。Prony算法根据信号辨识出的参数:频率fm、衰减因子am、幅值Am、相位θm如式(11)表达。
用Prony算法对Uc,I进行分析,频率趋于50×n Hz,衰减因子am趋于0的分量即为稳态分量Ucs,Is。
2.2 噪声对谐波阻抗计算的影响
在实际测量中总是避免不了噪声的影响,本文以白噪声模型加以说明,采用小波分解去噪,如图4、图5所示,噪声多表现为低频通常包含在CD1,CD2,CD3中,以门限阈值对小波系数进行处理实现噪声。
3 并联电容器组优化配置方案
上面分析了谐波放大与谐波阻抗的关系以及谐波阻抗的计算方法,基于计算得到的系统谐波阻抗值,下面将根据优化目标函数和约束条件对电容器组进行配置。
首先从电能质量角度考虑,谐波源发出的谐波电流经PCC注入系统侧和电容器支路,系统侧谐波电流必须满足电网电能质量标准的约束
[18]。GB/T 14549—1993《电能质量 公用电网谐波》明确规定了电网谐波电流限值,如表1所示。
1)目标函数
实际应用中高串抗率优先于低串抗率的电容器投入,这就造成低串抗率电容器动作次数相比高串抗率的电容器少,甚至基本不投入,这种投切方式容易造成高串抗率电容器的损坏而且也不经济,鉴于此,本文以所有串联电抗器的串抗率之和作为优化问题的目标函数
[18]算式见式(12):
式中:m1,m2为系统电容器的组数;K1,K2为电容器组串联电抗器的串抗率。本文以6%和12%作为仿真算例。
2)约束条件
①电能质量约束 根据GB/T 14549—1993《电能质量 公用电网谐波》,在本实施例中10 kV配电网电压等级下,注入系统3次及5次谐波电流的允许限值均为20 A,电容器组优化投切方案要满足此电能质量国家标准的2个方面约束(见式(13)),本文以3次和5次谐波数据为例。
电网电压总谐波畸变率计算公式如式(14)所示,其允许限值为THDmax=4%:
式(13)和式(14)中:Is_n为系统侧谐波电流;Ic_n为电容器支路谐波电流;Vk为第k次谐波电压有效值;V1为基波电压有效值。
②电容器工作条件约束 根据并联电容器装置设计运行规范,电容器所承受的基波电压和谐波电压的几何平方根(电压有效值)不超过额定电压的1.1倍;流过电容器的基波电流和谐波电流的几何平方根(电流有效值)不超过额定电流的1.3倍,见式(15):
式中:Ic_1,Ic_3,Ic_5和IcN分别为电容器的基波电流、3次电流、5次电流和额定工作电流;
Zc_1,Zc_3和Zc_5分别为电容器支路基波、3次阻抗和5次阻抗;
UcN为电容器额定工作电压。
③电容器组数约束 基于调度自动化系统的自动电压控制系统(AVC系统)提高了电网调度自动化水平、改善电压质量。调度自动化系统采集数据并分析是否有母线电压或关口功率因数越限。在确保电网与设备安全运行的前提下进行电压无功优化控制,最终AVC系统形成电容器组设备投切指令,实现无功补偿设备合理投入。如某时刻根据电网AVC指令需要投入电容器组数为1,现场已投入运行的电容器组数为2,此时可供优化配置的电容器总组数为3。那么,在优化配置中6%和12%串抗率电容器的组数m1,m2均不能超过可供优化配置的电容器总组数3,且策略中电容器总组数要与可供优化配置的电容器总组数一致,即m1≤3,m2≤3,m1+m2=3,图6为电容器组优化配置方案策略框图。
4 算例分析
4.1 谐波阻抗计算
以双馈线模型为例,对系统谐波阻抗进行估计,验证本文系统谐波阻抗估计方法的有效性和合理性[19-20],仿真模型如图7所示。图中,Zs和Us分别为系统侧等效谐波阻抗和等效电压,Zc_i和Ic_i(i=1,2)分别为馈线i支路的等效谐波阻抗和谐波电流源,在t=0.5 s时投入电容器,用采样频率为20 kHz的示波器记录PCC母线的电压和电流。采集PCC母线谐波数据,将信号经小波分解后原信号小波系数较大,噪声的小波系数较小,通过选取合适的阈值实现去噪,大于阈值的小波系数被认为是有信号产生的,应予以保留,小于阈值的则认为是噪声产生,置为0而被去除。图8为db5小波5层分解图,采用最大最小软阈值对采集的信号降噪。
采用Prony算法对去噪后的电流Ipcc进行辨识,包括频率fm、衰减因子am、幅值Am、相位θm,从而计算出暂态分量,表2是基于Prony提取的稳态分量,图9所示为暂态电流波形。
电压暂态分量计算过程相同,通过式(10)计算系统谐波阻抗,通过3次样条插值得到整个频域下的谐波阻抗值如图10所示。
根据图10所示的仿真结果,在3次谐波对应的150 Hz处,阻抗幅值与相角的理想值分别为Zs_real,3=12.16 Ω,Phasereal,3=78.83°;阻抗幅值与相角的计算值分别为Zs_cal,3=11.64 Ω,Phasereal,3=74.10°。在5次谐波对应的250 Hz处,阻抗幅值与相角的理想值分别为Zs_real,5=17.88 Ω,Phasereal,3=76.02°;阻抗幅值与相角的计算值分别为Zs_cal,3=18.74 Ω,Phasecal,3=80.20°,由此系统谐波阻抗的相角误差与幅值误差如图11所示。
4.2 并联电容器组优化配置
搭建10 kV配电网模型,其等效电路如图12所示。PCC处连接3条馈线,馈线1和2连接的电弧炉视为系统中的谐波源,仿真模型参数设置如下:系统短路容量(Sd)为100 MVA;电容器容量(QcN) 为2 500 kVar,额定电压(UN)为10/3 kV;系统阻抗(Zs) 为4.83 Ω;电容器容抗(Xc)為48.82 Ω。采集公共连接点母线的谐波数据并进行FFT分解,得到3次和5次谐波电流,分别为I3=26.85 A,I5=26.7 A。
当AVC系统下达调度指令需投入1组电容器,现场已投入运行的电容器组数为2,电容器组数约束条件为m1≤3,m2≤3,m1+m2=3,基于系统谐波阻抗和公共连接点实时谐波数据,采用(GA)遗传算法计算满足以上3条约束条件的最优解,迭代次数达到56次,得到计算结果为m1=2,m2=1,即在2组6%和1组12%串抗率电容器组投入运行时能够在满足约束条件下使目标函数最优,最优值为0.24,如图13所示。
据此对电容器组进行优化配置,能够合理分配高低串抗率电容器投切,提高系统运行的经济性。改变电弧炉谐波源大小和AVC调度指令,基于仿真模型对本文所提优化配置策略进行多次验证,做出的5次优化配置结果见表3。
由仿真结果可知,电抗率未优化配置时,12%串抗率电抗器使用次数占总投入次数的74%,6%串抗率电抗器仅使用5次;而采用本文所提的优化配置策略后12%串抗率电抗器使用次数占总投入次数的42%,6%串抗率电抗器使用11次。频繁使
用高电抗率的电容器会缩短设备寿命。而优化投切后,低电抗率电容器在满足电能质量约束条件下投入运行次数更多,由此可见优化投切后一定程度上降低了高串抗率的频繁使用和无功容量的损失。优化配置后各个限制条件仿真校验结果如表4所示。
根据仿真结果可知,该电容器组投切优化方案下系统电能质量以及电容器的设计运行规范均能满足约束条件。
5 结 语
针对现有变电站高、低串抗率电容器组不合理配置问题,建立了配电网仿真模型,依据系统谐波阻抗和谐波谐振对谐波源放大原理,在电网电能质量和电容器组运行工况约束下,对多串抗率电容器组进行优化配置,主要结论如下。
1)基于系统谐波阻抗的计算可得到系统侧和电容器组较为准确的谐波电压、电流计算数据,将计算数据作为电容器组的投切依据,制定多串抗率电容器组配置方案。
2)以电容器组的投切作为谐波阻抗计算方法具有功能上的便利性。谐波阻抗幅值和相角最大误差分别为4.8%和6%,证实了计算结果的准确性,可为并联电容器组配置提供数据支撑。
3)电容器组优化配置后,高串抗率电容器组投入频次下降32%,低串抗率电容器组投入频次由26%提高至58%,改善高串抗率电容器频繁投入造成的设备寿命损失和无功容量的浪费问题。
由于变电站有着严格的运行规范,电容器组的投切不能随意改变,故缺少了对实际系统的验证。在后续研究中将考虑以无功损耗和串抗率作为综合目标函数,对本文模型加以进一步完善。
参考文献/References:
[1] 杨洪耕,王磊.基于拉盖尔多项式的非线性负荷谐波发射水平估计[J].中国电机工程学报,2005,25(7):81-85.
YANG Honggeng,WANG Lei.Assessing harmonic emission levels from non-loads using Laguerre polynomials[J].Proceedings of the CSEE,2005,25(7):81-85.
[2] 孙媛媛,李树荣,石访,等.含分布式谐波源的配电网多谐波源责任划分[J].中国电机工程学报,2019,39(18):5389-5398.
SUN Yuanyuan,LI Shurong,SHI Fang,et al.Multiple harmonic source contribution determination in the active distribution network with distributed harmonic sources[J].Proceedings of the CSEE,2019,39(18):5389-5398.
[3] 李天楚,伍智鹏,朱明星.配电网谐波电流限值计算与评估的若干问题探讨[J].电力电容器与无功补偿,2016,37(6):7-11.
LI Tianchu,WU Zhipeng,ZHU Mingxing.Study on several issues concerning the calculation and evaluation of harmonic current limit value in distribution network[J].Power Capacitor & Reactive Power Compensation,2016,37(6):7-11.
[4] 王继隆,李盛伟,王楠,等.变电站并联电容器组配置及分闸过电压的仿真分析[J].电力系统及其自动化学报,2019,31(1):58-64.
WANG Jilong,LI Shengwei,WANG Nan,et al.Configuration of shunt capacitor bank in substation and simulation of opening overvoltage[J].Proceedings of the CSU-EPSA,2019,31(1):58-64.
[5] 陈柏富,杨言孝.并联电容器装置在变压器空载时投入引发串联谐振[J].电力电容器与无功补偿,2017,38(6):7-11.
CHEN Baifu,YANG Yanxiao.The series resonance problem of shunt capacitor bank when transformer in no-load condition[J].Power Capacitor & Reactive Power Compensation,2017,38(6):7-11.
[6] 翟運娟,韩本帅,于丽娜.并联电容器装置串联电抗器参数分析与选择[J].国网技术学院学报,2016,19(3):17-20.
ZHAI Yunjuan,HAN Benshuai,YU Lina.Parameter analysis and selection of series reactor in parallel capacitor device[J].Journal of State Grid Technology College,2016,19(3):17-20.
[7] 高泽明,程伦,胡文平,等.电网自动电压控制精细规则自动发现技术研究[J].电网技术,2022,46(1):378-386.
GAO Zeming,CHENG Lun,HU Wenping,et al.Research on automatic discovery technology of fine rules for automatic voltage control in power grid[J].Power System Technology,2022,46(1):378-386.
[8] 林峰,梁一桥,吕佳铭,等.10kV配電线路串、并联混合电容器补偿技术研究[J].电力电容器与无功补偿,2019,40(3):10-15.
LIN Feng,LIANG Yiqiao,LYU Jiaming,et al.Study on compensation technology of series and parallel mixed capacitor at 10 kV distribution line[J].Power Capacitor & Reactive Power Compensation,2019,40(3):10-15.
[9] 朱建华,徐刚刚,刘鹏飞,等.并联电容器装置接地和电抗率选取建议[J].电力电容器与无功补偿,2017,38(5):7-11.
ZHU Jianhua,XU Ganggang,LIU Pengfei,et al.Selection advice on grounding and reactance ratio of shunt capacitor[J].Power Capacitor & Reactive Power Compensation,2017,38(5):7-11.
[10]TUSHAR M H K,ASSI C.Volt-VAR control through joint optimization of capacitor bank switching,renewable energy, and home appliances[J].IEEE Transactions on Smart Grid,2018,9(5):4077-4086.
[11]陈伯胜.串联电抗器抑制谐波的作用及电抗率的选择[J].电网技术,2003,27(12):92-95.
CHEN Bosheng.Harmonics restraining function of serial reactor and selection of reactance rate[J].Power System Technology,2003,27(12):92-95.
[12]郝福忠,赵锋,李晋城,等.考虑电网谐波影响的电容器投切研究[J].电力系统保护与控制,2011,39(4):79-83.
HAO Fuzhong,ZHAO Feng,LI Jincheng,et al.Research of capacitor switching considering harmonic influence[J].Power System Protection and Control,2011,39(4):79-83.
[13]张程,王主丁,张宗益,等.多负荷水平下配电网电容器优化配置算法[J].电网技术,2010,34(12):85-89.
ZHANG Cheng,WANG Zhuding,ZHANG Zongyi,et al.An algorithm for optimal configuration of capacitors in distribution network under multi-load levels[J].Power System Technology,2010,34(12):85-89.
[14]俞永军,张帆,骆福权,等.一种电容器组串联电抗器谐波过载保护的实现方法[J].电力电容器与无功补偿,2019,40(6):54-57.
YU Yongjun,ZHANG Fan,LUO Fuquan,et al.Achievement method on harmonic overload protection for series reactor of capacitor bank[J].Power Capacitor & Reactive Power Compensation,2019,40(6):54-57.
[15]邬光耀,徐永海,洪旺松.并联电容器串抗率的选择方法研究[J].机电信息,2014(6):21-23.
WU Guangyao,XU Yonghai,HONG Wangsong.Research on the selection method of series reactance ratio of parallel capacitors[J].Mechanical and Electrical Information,2014(6):21-23.
[16]ABEDINI M,DAVARPANAH M,SEPEHR A,et al.Shunt capacitor bank:Transient issues and analytical solutions[J].International Journal of Electrical Power & Energy Systems,2020,120:106025.
[17]肖湘宁,韩民晓,徐永海,等.电能质量分析与控制[M].北京:中国电力出版社,2010.
[18]余欣梅,李妍,熊信艮,等.基于PSO考虑谐波影响的补偿电容器优化配置[J].中国电机工程学报,2003(2):30-34.
YU Xinmei,LI Yan,XIONG Xinyin,et al.Optimal shunt capacitor placement using particle swarm optimization algorithm with harmonic distortion consideration[J].Proceedings of the CSEE,2003(2):30-34.
[19]王行亚,肖先勇,吴俊,等.基于线性度校验的二元线性回归系统谐波阻抗估计方法[J].中国电机工程学报,2020,40(9):2826-2834.
WANG Hangya,XIAO Xianyong,WU Jun,et al.Utility harmonic impedance estimation based on binary linear regression with linearity calibration[J].Proceedings of the CSEE,2020,40(9):2826-2834.
[20]徐方维,王川,郭凯,等.基于无相位实测数据的系统侧谐波阻抗估计方法改进[J].中国电机工程学报,2021,41(9):3149-3157.
XU Fangwei,WANG Chuan,GUO Kai,et al.An improved utility harmonic impedance estimation method based on measurement data without phase angle[J].Proceedings of the CSEE,2021,41(9):3149-3157.

