发散思维
小远
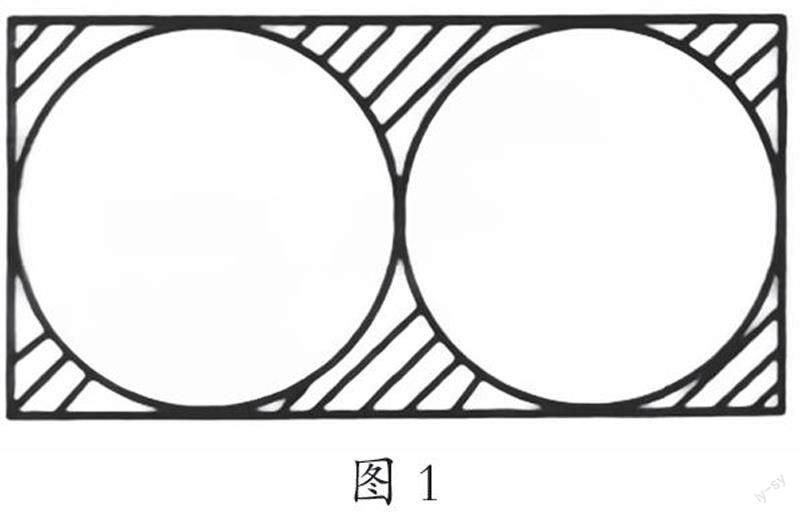
发散思维是创造性思维最主要的特点,它为人们创新源泉的流淌提供了宽广的大道。这里有一道数学题目,如图1所示,两个同样大小的圆正好放在一个长方形内。聪明的小朋友,你能不能担任小老师,为这道题目添加一个条件,求出阴影部分的面积呢?
注意!这道题目可以添加的条件有很多,添加不同的条件后,题目的难度不同,解题方法也不同。
方法一:添加条件“长方形的宽是5厘米”。
1.分析
从图1可以看出,长方形的宽等于圆的直径,知道了长方形的宽,自然也就知道了圆的直径。长方形的长是两个直径,所以,长方形的长是宽的2倍。最后,用长方形的面积减去两个圆的面积即可得到阴影部分的面积。
2.解题过程
长方形的长:5×2=10(厘米)
长方形的面积:10×5=50(平方厘米)
单个圆的面积:3.14×(5÷2)2=19.625(平方厘米)
阴影部分的面积:50-19.625×2=10.75(平方厘米)
所以,阴影部分的面积为10.75平方厘米。
方法二:添加条件“圆的半径是5厘米”。
1.分析
圆的半径是5厘米,直径就是10厘米。所以长方形的宽是10厘米,长是20厘米。最后,用長方形的面积减去两个圆的面积即可得到阴影部分的面积。
2.解题过程
长方形的宽:5×2=10(厘米)
长方形的长:10×2=20(厘米)
长方形的面积:20×10=200(平方厘米)
单个圆的面积:3.14×52=78.5(平方厘米)
阴影部分的面积:200-78.5×2=43(平方厘米)
所以,阴影部分的面积是43平方厘米。
方法三:添加条件“圆的周长为6.28厘米”。
1.分析
知道了圆的周长,就可以计算出圆的直径和半径,进而得到长方形的长、宽。最后,用长方形的面积减去两个圆的面积即可得到阴影部分的面积。
2.解题过程
圆的直径:6.28÷3.14=2(厘米)
长方形的长:2×2=4(厘米)
长方形的面积:4×2=8(平方厘米)
单个圆的面积:3.14×(2÷2)2=3.14(平方厘米)
阴影部分的面积:8-3.14×2=1.72(平方厘米)
所以,阴影部分的面积是1.72平方厘米。
除了添加以上三种条件,这个题目还可以添加其他条件来解答。聪明的你不妨发散一下思维,看看能想出多少种不同的方法。

