儿童数字线估计：不同范围和长度情境的影响

曹碧华?曾婷?廖虹?李富洪

摘 要 选取127名儿童完成数字线估计任务，探讨其在不同类型的复杂情境中对熟悉数字的估计策略。两个实验分别要求儿童对10cm长度下的不同范围（0～50和0～100），以及不同长度（10cm和18cm）对0～100范围的数字进行估计。结果显示儿童对0～50估计时绝对误差百分比曲线呈直线上升型，而对0～100范围的数字估计呈“M”型。针对范围和长度的变化，儿童分别采取心理长度和比例判断等估计策略，但受不同范围的影响更大。这表明儿童会根据具体情境灵活选择不同的估计策略，为重叠波理论提供了新的证据。

关键词 儿童；数字估计；情境；心理长度；比例判断

分类号 B842.3

DOI：10.16842/j. cnki. issn2095-5588.2023.05.001

1 引言

估计在儿童的学习中无处不在，例如估计作业和考试成绩、文具价格等。估计能力是早期数学认知发展的关键基础，对儿童数学的成就和认知能力的发展非常重要（Siegler & Booth， 2004）。其中，数字估计指数量表征转换过程中涉及的对数字的估计（莫雷等， 2010; Slusser & Barth， 2017）。研究儿童数字估计最典型的是数字线估计任务，它要求儿童在标有起点和终点的数字线上给某数字标出位置。儿童在数字线估计任务中主要存在线性表征和对数表征两种形式（Dehaene， 1997; Siegler & Booth， 2004）。线性表征是对数字的精确表征，指个体对数字进行表征的心理距离相等，相邻数字间的心理距离不会随着数字的增加而改变（Case & Okamoto， 1996）。对数表征则是不精确的，指随着需表征的数字的增加，个体相应的心理距离表现出前疏后密的特点（Dehaene， 1997）。

重叠波理论认为任何年龄阶段的儿童都知道并会使用多种相互竞争的方法（例如策略和规则）及表征模式，具体运用哪种策略和规则主要取决于问题和情境（莫雷等， 2010; Siegler， 1996）。以往研究主要考察儿童在简单情境中对数字估计的表征模式和估计策略，不同年龄的儿童仅需对相同范围或相同长度的数字进行估计（周广东等， 2009; Opfer et al.， 2016; Slusser & Barth， 2017）。近年来，研究者更关注儿童在复杂情境中数字线估计的发展趋势及策略。此时，儿童须估计两种不同范围或不同长度下的数字。结果发现情境会影响儿童对数字的表征模式和估计策略的选择（曹碧华等， 2021; 莫雷等，2010; 臧蓓蕾， 張俊， 2017; Zang et al.， 2019）。莫雷等（2010）发现一年级儿童的表征模式受到不同范围和长度的影响。当长度为15cm时，一年级儿童在0～100范围采用线性表征，而在0～1000范围采用对数表征。当长度为10cm和20cm时，在0～1000范围内随着长度的增加，线性表征占优势。臧蓓蕾等（2017， 2019）发现3～5岁学龄前幼儿在1～5、1～10和1～20三种小范围内的不同数距条件下会使用不同的表征模式。

探究表征模式只是为了解释儿童对不同数字估计准确性的问题，研究者应该更关注其背后的心理加工方式或策略的使用规律（刘国芳， 辛自强， 2012）。儿童估计数字时常使用参照点策略，它是指将线段的起点、中点、四分位点和终点作为参照点或根据自身产生的锚定点完成估计（邢强等， 2015; Barth & Paladino， 2011; Peeters et al.， 2016; Rouder& Geary， 2014）。在数字线估计中，儿童将需估计的数字与参照点进行比较，把数字之间的关系转换成空间表征，即根据参照点的位置确定估计数字的位置（Sullivan & Barner， 2014）。即使采用了参照点策略，儿童在数字线任务中也可能会采取更高级的估计策略（刘国芳， 辛自强， 2012; 臧蓓蕾等， 2019）。数包括名称、等级、等距和等比四大属性。当以起点为参照点时，一年级儿童会将低端数字与固定的长度相对应，这就是心理长度。无论需要估计的数字的范围和长度如何改变，估计低端数字1～10时都存在心理长度。这表明儿童给数字“1”赋予了心理长度，并通过叠加数数策略对其他数字进行估计，体现了儿童对等距属性的认识（曹碧华等， 2021; 莫雷等， 2010; 张帆等， 2015）；当以中点为参照点时，在标有“0”和“100”的数字线上估计“50”时，儿童会把部分（50）置于整体（100）中，即基于范围的比例来估计数字（Barth & Paladino， 2011; Slusser & Barth， 2017），体现了儿童对等比属性的认识；当以终点为参照点时，如选择密度相同的后十个末端数字要求儿童估计，有些末端数字也符合心理长度的预期，故不能完全排除儿童也采用倒数心理长度策略（曹碧华等， 2021; 莫雷等， 2010）。莫雷等（2010）认为一年级儿童在估计0～100和0～1000的低端数字时存在心理长度，但估计0～1000时倾向对数表征，说明其对数的认识尚未达到等比水平。我们认为这与一年级儿童不熟悉0～1000范围的数字和不知道1000是100的10倍有关。那么如果呈现儿童熟悉的小范围数字，且他们知道数字及长度之间的倍数关系时，儿童估计数字时是否能达到等比属性水平？

本研究的目的是考察儿童在不同类型的复杂情境中估计熟悉范围数字时采用的策略。实验一要求被试估计0～50和0～100两种熟悉范围的数字。如果一年级儿童估计所有低端数字时稳定地存在心理长度，那么本研究中儿童估计低端数字也存在心理长度，并且随着年龄的增长，二年级儿童心理长度的范围会减少（曹碧华等，2021;莫雷等， 2010）。值得注意的是，以往研究并未考察估计顺序是否对策略产生影响。尽管大班和一年级儿童尚未学习乘法，但已经知道50是100的一半，可能凭直觉进行比例判断（Barth & Paladino， 2011; Slusser & Barth， 2017）。本研究中一、二年级儿童均需估计0～50和0～100两种范围的数字，对中端和末端数字的估计可能会受到估计顺序的影响，即儿童先锚定估计范围数字的实际长度，继而以一定的方式影响后估计的数字范围。然而，是先完成0～100会影响0～50的估计，还是先完成0～50会影响0～100的估计尚不明确。因此，本研究将首次探讨估计顺序对儿童熟悉范围数字估计的影响。

实验二要求被试在10cm和18cm两种长度（1∶1.8）下对0～100进行数字估计（曹碧华等， 2021）。相对于不同范围的感知，儿童对线段长度、高度和面积等知觉线索的判断可能更为敏感和直观（Hollands & Dyre， 2000; Sella et al.， 2015; Siegler & Opfer， 2003）。因此，我们推测在0～100熟悉的范围内，两个年级儿童会根据不同的线段长度调整估计策略，对低端和末端数字的心理长度范围更小，而对中端数字的估计更可能采用比例判断策略。

更重要的是，本研究在两个实验中均设置了相同的实验条件，即10cm长度下对0～100范围的数字估计。我们将对比分析0～100（10cm）范围儿童在两个实验不同情境的估计策略，进一步探讨其是否因受到0～50（10cm）和0～100（18cm）两种不同情境的影响而使用灵活的估计策略。

2 实验一

2.1 方法

2.1.1 被试

采用G*power 3.1.9软件进行计算（Faul et al.， 2007）。对于本实验适用的重复测量方差分析，中等效应量f=0.25且显著性水平α=0.05时，预测达到95%的统计力水平的总样本量至少为54。我们共选取了63位兒童参与本实验，其中一年级儿童33 名，男生20名，女生13名（M=7.38岁，SD=0.68）；二年级儿童30名，男生17名，女生13名（M=8.41岁，SD=0.61）。由于一名一年级儿童没有理解指导语，对所有数字估计的实际长度均在中点附近；三名二年级儿童对较多数字未划线估计导致数据缺失，故这四名儿童的数据不予分析。

2.1.2 材料

实验材料为两个31页纸的小册子，第一页登记被试基本资料（包括性别、年龄及班级），其余30 页为正式的实验材料，每一页纸中间印有一条长10cm的数字线， 两端分别标为0和50（100），中间无任何标记。数字线中间上方2cm 处的圆圈里随机呈现一个让被试估计的数字。实验一在0～50和0～100范围的数字如下：

0～50：1、2、3、4、5、6、7、8、9、10、21、22、23、24、25、26、27、28、29、30、40、41、42、43、44、45、46、47、48和49。

0～100：1、2、3、4、5、6、7、8、9、10、46、47、48、49、50、51、52、53、54、55、90、91、92、93、94、95、96、97、98和99。

2.1.3 实验程序

采用纸笔测验法集体施测，禁止被试之间交流。被试在小册子的第一页填完基本信息后，被告知将做一个关于数字估计的测试。从第二页开始是测试的题目，结果不计入学业成绩。每一页的正中间有一条数字线，左端标有“0”，右端标有“50”（或“100”）。如果左边表示“0”，右边表示“50”（或“100”），那么圆圈里的数字应该在哪一个位置？请想好后用笔在线段上划一条竖线来表示数字的位置。实验过程中不能用直尺，也无任何反馈。每名被试都做两种范围的估计。为平衡和探讨顺序效应，一半被试先做0～50的估计，再做0～100的数字估计，另一半被试则相反。主试用直尺测量被试的估计结果（精确到毫米），再将实际长度转化估计值（实际长度除以线段长度乘以范围）进行分析。

2.2 结果

2.2.1 不同范围下实际长度估计的比较

首先，为考察当范围由0～50变化至0～100时儿童对数字估计是否存在心理长度，分别测量儿童估计的低端数字（1～10）、中端数字（21～30）和（46～55）的实际长度，即从起点0到数字线上标记位置之间的距离；以及末端数字（40～49和90～99）的实际长度，即分别从终点50和100到数字线上标记位置之间的距离。然后，对两种范围下的实际长度做配对t检验。如果两者的长度无显著差异，则表明存在心理长度。

结果显示一年级儿童对所有低端数字（1～10）估计的实际长度并不随着范围的增大而发生变化。这表明即使范围增大了2倍，一年级儿童仍将低端数字与某一固定的线段长度相对应，即存在心理长度。二年级儿童估计1～8范围内的数字时其实际长度未随范围改变而发生相应的变化（表1）。估计中端数字时，一、二年级儿童仅分别有四个和三个数字对差异不显著，无法说明儿童对此存在心理长度。估计末端数字时，两个年级儿童对所有数字对估计的实际长度差异显著（ps< 0.001），不存在心理长度。

其次，儿童在估计中端和末端数字时不存在心理长度，故进一步考察是否进行了比例判断。由于100是50的2倍，将0～100中端和末端数字的实际长度均乘以2，与0～50对应数字的实际长度进行配对t检验，如果两者的长度无显著差异，则表明存在比例判断。结果表明对末端数字估计时，一年级除49-99外，40-90、41-91、42-92、43-93、44-94、45-95、46-96、47-97和48-98这9个数字对没有显著差异；二年级除40-90和49-99外，41-91、42-92、43-93、44-94、45-95、46-96、47-97和48-98这八个数字对无显著差异。这说明一、二年级儿童对末端数字估计时基本上进行了比例判断，达到等比水平（图1）。

2.2.2 表征模式

以随机呈现的数值（实际值）为自变量，被试估计值的中位数为因变量（选中位数是为了排除极值的影响），选取线性和对数两种表征模式进行曲线拟合。结果表明两个年级儿童均更好地拟合了线性模型，一年级在0～50范围，R2lin=0.97>R2log=0.85；0～100：R2lin=0.99>R2log=0.86。对两模型预测值残差的配对t检验，结果显示对数和线性模型拟合度差异显著，0～50：t（29）=-8.62，p< 0.001；0～100：t（29）=-8.00，p< 0.001。二年级在0～50范围：R2lin=0.96> R2log=0.80；0～100：R2lin=0.98> R2log=0.84。两模型预测值残差的配对t检验结果显示，对数和线性模型拟合度差异显著，0～50：t（29）=-8.71，p< 0.001；0～100：t（29）=-7.45，p<0.001。

为检验个体中位数与总体估计的拟合结果是否一致，先对每个被试的估计进行曲線拟合。然后，计算儿童对0～50和0～100的数字估计所进行线性表征、对数表征以及在两种表征之间摇摆不定（即对数拟合和线性的预测力无显著差异）的人数百分比。结果显示在0～50范围，一、二年级采用线性表征的儿童分别占50%和48%，对数表征分别占9%和0%，在两者间摇摆的分别占41%和52%。在0～100范围，一、二年级符合线性表征的儿童分别为69%和92%，对数表征分别占6%和0%，两者间摇摆的分别占25%和8%。最后，分别对两个年级儿童线性表征的人数百分比进行独立样本t检验，结果显示在0～100范围，两个年级儿童的线性表征人数百分比差异显著，t（57）=-2.33，p=0.023。这表明随着年龄的增长，使用线性表征的儿童越来越多。

2.2.3 估计的准确性

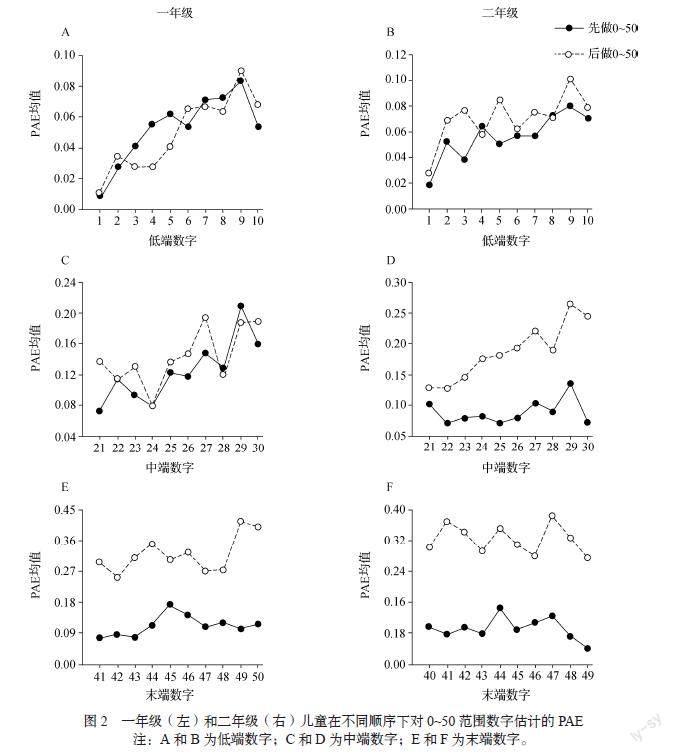
采用绝对误差百分比（Percent Absolute Error，简称PAE）作为评价儿童数字估计准确性的指标，计算公式为：PAE=|估计值-实际值|/范围，求出儿童在各段的平均PAE。由于儿童对中端和末端数字实际长度估计时可能采用了比例判断的策略，为了考察其原因，对个体平均PAE进行2（估计顺序：先做0～50，后做0～50）× 2（年级：一年级， 二年级）×2（范围：0～50，0～100）×3（数字位置：低端、中端和末端）的重复测量方差分析。其中，估计顺序和年级为被试间变量，范围和数字位置为被试内变量。结果表明估计顺序、范围和数字位置的主效应均显著，估计顺序：F（1， 28）=38.25，p< 0.001， η2=0.59；范围：F（1， 56）=125.98，p< 0.001， η2=0.82；数字位置：F（2， 86）=59.22，p< 0.001， η2=0.69。估计顺序与范围的交互作用显著，F（1， 28）=78.81，p< 0.001， η2=0.75。简单效应分析表明，在0～50范围，先做的PAE值（9.07%）显著低于后做的（18.02%），p< 0.001，说明先做的估计准确性更高（图2）。估计顺序与位置的交互作用显著，F（2， 86）=15.82，p<0.001， η2=0.37，表现为对中端数字估计时，先做0～50的PAE值（9.50%）显著低于后做（12.86%），p< 0.001。范围与位置的交互作用显著，F（2， 86）=90.56，p< 0.001， η2=0.77。简单效应分析表明，儿童对0～50范围内低端（5.74%）、中端（13.67%）和末端（21.22%）数字的PAE两两之间均存在显著差异，ps< 0.001。另外，0～50中端和末端数字的PAE均显著高于0～100的中端（8.48%）和末端（8.68%）数字，ps< 0.001，表明两个年级儿童对0～100中端和末端数字的估计准确性更高。

为进一步分析儿童数字估计准确性是否受不同参照点的影响，分别在不同范围的低端、中端和末端共取十个估计数字的PAE进行平均（Ashcraft & Moore， 2012）。结果表明在两种范围内，两个年级儿童PAE均值变化模式相同。0～50范围内，均呈直线上升型，PAE均值随着估计数值的增大而增大，即儿童在数字线估计时将起点作为参照点。在0～100范围估计的PAE均值呈“M”型，在靠近两端点和中点位置PAE均值更低，即儿童在数字线估计时，能将两端点和中点作为参照点。与方差分析结果一致，发现0～100的PAE均值更低，说明估计准确性更高（图4A）。

实验一表明儿童估计低端数字时存在心理长度，估计末端数字时则可能使用了比例判断策略。这表明儿童对熟悉范围低端数字的变化不敏感，但对末端数字的变化更为敏感。然而，尚不清楚儿童对长度的变化是否敏感。因此，实验二考察当固定范围为0～100时，改变长度后儿童在数字线估计中是否仍存在心理长度或比例判断。

3 实验二

3.1 方法

3.1.1 被试

G*power计算结果同实验一。共选取64名儿童参与本实验，其中一年级儿童31名， 男生18名， 女生13名（M=7.25岁，SD=0.46）；二年级儿童33名，男生18名，女生15名（M=8.25岁，SD=0.31）。

3.1.2 材料

实验材料与实验一基本相同。在每一页纸中间印有一条长10cm或18cm的数字线，其两端分别标为“0”和“100”。数字线中间上方2cm处的圆圈里随机呈现一个让被试估计的数字。研究范围为0～100，同样在低端、中端和末端各选十个数字（与实验一0～100范围的完全相同）。

3.1.3 实验程序

与实验一相同。

3.2 结果

3.2.1 儿童在不同长度下实际估计长度的比较

首先考察数字线长度由10cm变化至18cm时儿童在估计0～100范围内数字时是否存在心理长度，具体测量和计算方法与实验一相同。然后对相同数字在两种条件下的实际长度做配对t检验。结果显示在两种不同长度下估计低端数字时，一年级儿童对1～7，9和10的实际长度无显著差异，二年级儿童对1～5和9的实际长度无显著差异（表2）。

在两种不同长度下估计中端数字时，两个年级儿童均存在显著差异，ps< 0.001，即不存在心理长度；估计末端数字时，一、二年级儿童对94～99六个数字和97～99三个数字的估计无显著差异，符合心理长度的预期。由于对最末端部分连续的数字存在心理长度，故不能排除儿童对部分末端数字估计时使用倒数心理长度策略。然而，由于末端有些数字的实际长度未出现一致的趋势，也不能说明使用倒数的心理长度策略。

其次，由于儿童对中端数字的估计不存在心理长度，故进一步考察是否进行了比例判断。根据18cm和10cm的倍数关系，将10cm中端数字的实际长度乘以1.8后，与18cm相同数字的实际长度进行配对t检验。结果表明一年级儿童除46和50以外，另八个数字在两种长度下均无显著差异。二年级儿童估计数字46～49和55时，两种数字线的实际长度无显著差异。这表明估计中端数字时，两个年级儿童根据长度的关系进行了比例判断（图3）。

3.2.2 表征模式

以随机呈现的数值为自变量，被试估计值的中位数为因变量，选取线性及对数两种表征模式对儿童数字估计结果进行曲线拟合。结果表明在不同长度下，一、二年级儿童在0～100范围内均更好地拟合线性表征。当一年级的长度为10cm：R2lin=0.99 >R2log=0.87；18cm：R2lin=0.99>R2log=0.88。二年级的长度为10cm：R2lin=0.99>R2log=0.86；18cm：R2lin=0.99>R2log=0.84。两模型预测值残差的配对t检验结果显示对数与线性模型拟合度差异显著。当一年级长度为10cm：t（29）=-8.63，p<0.001；18cm：t（29）=-7.91，p<0.001。二年级10cm时：t（29）=-7.41，p <0.001；18cm：t（29）=-11.39，p< 0.001。

对个体估计进行曲线拟合，计算当长度为10cm和18cm时，一年级儿童采用线性表征的分别为84%和91%，对数表征各占3%，在两种表征摇摆的分别为13%和7%。二年级儿童采用线性表征的分别为88%和97%，摇摆不定的分别占12%和3%。这说明随着年龄的增长和长度的增加，两个年级采用线性表征的儿童逐渐增多。最后，分别对两个年级儿童线性表征的人数百分比进行独立样本t检验，结果不存在显著差异。

3.2.3 估计的准确性

计算方法同实验一，分别求出儿童在各端的平均PAE。然后，进行2（年级：一年级，二年级）×2（长度：10cm，18cm）×3（数字位置：低端、中端和末端）的重复测量方差分析。结果表明年级、长度和位置的主效应均显著，年级：F（1，62）=19.16，p< 0.001，η2=0.24；长度：F（1，62）=5.02，p=0.029，η2=0.075；数字位置：F（2，124）=10.70，p<0.001，η2=0.15。年级与位置的交互作用显著，F（2，124）=4.87，p=0.009，η2=0.073。位置与长度的交互作用也显著，F（2，124）=12.78，p<0.001，η2=0.17。另外，年级、长度和数字位置的三维交互作用显著，F（2，124）=4.67，p=0.011，η2=0.07。简单效应分析表明，当长度为10cm时，一年级儿童对低端（7.82%）和中端数字（7.04%）估计的PAE均显著低于末端（10.60%）数字，ps< 0.01；二年级儿童对中端数字（4.80%）估计的PAE显著低于末端数字（7.15%），p=0.039。这说明在10cm长度下，末端数字估计的准确性更低。当长度为18cm时，一年级儿童对低端数字的PAE（4.49%）分别低于中端（10.41%）和末端数字（8.34%），ps<0.001。然而，二年级儿童在低端（3.45%）、中端（3.88%）和末端（5.27%）数字的PAE很低，且两两差异均不显著，说明他们对所有数字估计的准确性都很高。

为进一步分析数字估计的准确性，分别在不同长度数字线的低端、中端和末端共十个估计数字的PAE进行平均（Ashcraft & Moore， 2012）。结果发现PAE均值变化模式相同，均呈“M”型。估计低端数字时，PAE均值随估计数字的变大而增大，在起点估计精确性最高；估计中端数字时，PAE均值在中点位置明显下降；估计末端数字时，距离终点越近PAE均值越小。这些结果说明儿童在数字线估计时，能将两端点和中点作为参照点（图4B）。

3.3 儿童两个实验对0～100（10cm）估计的PAE的比较

为考察儿童在0～100（10cm）条件下PAE是否受不同实验情境的影响，对两个实验儿童估计的PAE进行2（实验：实验一，实验二）×2（年级：一年级，二年级）×3（数字位置：低端、中端和末端）重复测量方差分析。其中，实验和年级为被试间变量，数字位置为被试内变量。结果表明数字位置的主效应显著，F（2，114）=8.66，p<0.001，η2=0.13。实验和数字位置的交互作用显著，F（2，114）=3.29，p=0.041，η2=0.06。简单效应分析表明实验一中端数字的PAE（7.82%）显著高于实验二（5.92%），p=0.006，即实验二中端数字准确性更高（表3）。

4 讨论

本研究首次考察了在不同类型的复杂情境下儿童对熟悉范围数字的估计策略，主要有三个新发现：一是估计顺序会影响儿童对不同范围数字的表征模式和估计策略。二是无论是数字范围还是数字线长度发生变化，儿童对低端、中端和末端数字分别采取心理长度和比例判断等估计策略，且受不同范围的影响更大。三是即使实验条件相同0～100（10cm），儿童也会受到不同情境的影响，对中端数字使用灵活的估计策略。这些结果表明，一、二年级儿童对熟悉范围数字的认识已达到等距和等比水平，且能根據不同情境采取灵活的估计策略，为重叠波理论提供了新的证据。

4.1 不同范围情境的估计策略

本研究发现即使是熟悉范围的数字，一年级儿童对低端数字估计仍存在心理长度。心理长度指儿童将低端数字与固定长度对应起来，反映儿童对数的认识达到等距水平（莫雷等， 2010）。在测试的小册子上，部分儿童用铅笔画点或小竖线作的标记，如数数一样。即通过将“1”赋予一定的长度，使用叠加数数的策略（曹碧华等， 2021; 莫雷等， 2010）。这支持了一年级儿童在开始接受正规教育的早期，倾向于将低端数字与固定的长度对应起来。随着数字变大，他们可能发现终点数字的变化，逐渐放弃叠加数数的策略（张帆等， 2015）。莫雷等（2010）认为心理长度反映儿童高估低端数字的实际长度，并导致估计0～1000内的数字时更好地拟合对数表征。然而，本研究表明低端数字的心理长度也能解释线性表征，这与莫雷等（2010）的解释不一致。这说明儿童估计低端数字时存在心理长度是稳定的现象，与表征模式的关系需要根据不同的任务来决定。

有趣的是，本研究首次发现估计顺序会影响儿童估计0～50范围数字时的表征模式和策略。尽管0～50范围儿童估计的总体表征模式为线性表征，但个体曲线拟合结果表明一、二年级采用线性表征的儿童分别仅占50%和48%，这可能有两方面的原因：一方面，先估计0～50范围时，两个年级儿童末端先做的PAE值显著低于后做，说明先做的估计准确性更高。但先估计0～100范围，后估计0～50范围时，两个年级对末端数字40～49的估计都受到0～100末端的影响。儿童可能先将0～100估计的实际长度在大脑中进行锚定，再对40～49数字使用比例判断策略。具体表现为根据二者的倍数关系，从终点往前数数时按比例扩大2倍，再划线标记。这些结果说明儿童大脑中对末端40～49的表征虽较准确，但会受到50是100的一半的影响，即根据二者的数量关系相应地调整估计策略（臧蓓蕾等， 2019；Barth & Paladino， 2011）。

另一方面，估计0～50的中端数字时呈现出年级差异。一年级儿童先做和后做0～50的PAE曲线接近且有一定的重合，说明他们可能已经意识到了范围的不同。二年级儿童先做0～50的PAE曲线与后做的存在较大分离，其程度与末端数字的两条曲线相似。其中，先做0～50的估计准确性更高，但先做0～100再做0～50范围内的数字估计，准确性更低。

4.2 不同长度情境的估计策略

对不同长度情境下0～100范围内的数字进行估计时，儿童对低端数字的心理长度范围进一步缩小，一、二年级儿童分别仅对1～7和1～5的连续数字采取了叠加数数的策略。这表明随着低端数字的增大，儿童逐渐察觉到了长度的变化并随之调整了估计策略。估计末端数字时，一、二年级儿童分别对94～99六个数字和97～99三个数字的估计符合心理长度的预期，部分说明他们使用了倒数的心理长度策略。有意思的是，这与儿童在不同范围下对末端数字采取比例判断策略存在差异。与不同长度相比，儿童对不同范围的末端数字变化更敏感，会根据数字关系调整估计策略。

然而，两个年级儿童对中端数字估计时可能存在比例判断。这说明数字在线段上的位置相对靠后时，儿童可能才发现线段长度发生了很大变化，于是放弃继续将每个数字与固定长度相联系的数数策略（张帆等， 2015;Sietske et al.， 2013）。由于一年级儿童未学习乘法，故估计中端数字时的比例判断可能与直觉有关（Barth & Paladino， 2011; Slusser & Barth， 2017）。相反，二年级儿童开始学习乘法，故其比例判断可能与倍数有关。然而，儿童并非对所有的中端数字都存在比例判断，说明其比例判断仍处于发展状态。

与不同范围相比，两个年级儿童对线段不同长度的判断更准确。以往研究发现与阿拉伯数字所表示的数量信息相比，大班及以上年級的儿童对线段长度和面积大小等知觉线索更为敏感，类似于比例判断（Barth & Paladino， 2011; Booth & Sigler， 2006; Sella et al.， 2015; Spence， 1990）。Booth和Sigler（2006）要求儿童完成画线段和估计线段长度两种任务。结果发现随着年龄的增长，画线段任务的估计精确性提高，而估计线段长度任务的成绩与年龄无关，表明儿童对线段长度也有非常好的估计能力。

4.3 0～100（10cm）在两种不同情境下的估计策略

即使实验条件相同0～100（10cm），儿童的估计策略和PAE也会受到两个实验中不同情境的影响。结果表明0～100（10cm）的PAE都较低且呈现出“M”型，反映了儿童能有效地使用中点策略和两端点策略。这可能与儿童在学习和生活中对0～100的数字更熟悉、经验更丰富有关。Wall等（2016）认为数字的熟悉度会影响儿童数字估计的准确性，尽管0～50的范围较小，但儿童对0～100更为熟悉。进入小学后，作业和考试的评分大多为百分制，导致儿童不仅对100更熟悉，而且对90～99范围内的数字熟悉度也更高。

然而，两个实验中端数字的PAE存在显著差异，具体表现为在不同范围下，0～100中端数字的PAE显著高于不同长度的情境。这说明儿童根据情境的不同，对0～100（10cm）的中端数字灵活地使用了不同的估计策略。实际上，从中端数字实际的估计长度来看，两个年级儿童在不同范围的情境下既不存在心理长度，也未使用比例判断策略。然而，在不同长度的情境下，一、二年级儿童分别有八个和六个中端数字使用了比例判断策略。这说明儿童不仅对线段长度的变化更敏感，还能根据二者长度的关系调整策略以使估计更准确。基于数字和整体范围的比例关系，儿童容易准确标出50在0～100数字线上的位置（张帆等， 2015; Barth & Paladino， 2011; Slusser & Barth， 2017）。

数字估计能力与数学成绩存在正相关，在数字线估计任务中呈现出线性表征的儿童，其数学计算成绩往往好于对数表征的儿童（Booth & Siegler， 2006）。整数的数字线估计成绩与分数的数字线估计呈正相关，说明对整数的估计有助于提高儿童的分数表征能力（张丽等， 2014）。然而，数学学习困难的儿童在数字线估计中表现相对较差（Geary， 2011）。由此可以看出数字线估计研究的重要性，对培养儿童数学和认知能力起了引导和推动作用（刘国芳， 辛自强， 2012）。对小学数学教学的建议为，教师在进行数字比较大小和数字比例教学时，可以使用数字线估计任务辅助教学，采用不同范围大小数字且强调特殊点（两端点、中点和四分位点）的关系，帮助儿童理解数字之间的关系。同时，在进行这一任务的过程中要及时提供反馈，提高估计的准确性（Booth & Siegler， 2006; Siegler & Opfer， 2003）。另外，对于数学计算成绩较差的儿童可以使用数字线估计任务测试其数字估计能力，并通过观察估计策略的使用来判断儿童的认知水平（Joram et al.， 2005）。对于数字估计存在问题的儿童尽早干预，为提高他们的数学认知能力打好基础。

本研究也存在一些不足。以往研究选择估计的数字除低端和末端以外，还在每十个数中平均选择1～2个数字，这样对表征模式进行曲线拟合时更为全面。本研究虽包括低端、中端和末端三个区间的数字，但并未在其他部分的每十个数中选择1～2个数字，这可能会在一定程度上影响曲线拟合估计的结果。后续研究可在每十个数中平均增加一些数字，要求儿童进行估计。

5 结论

本研究的两个实验分别考察在不同类型的复杂情境下儿童数字估计的策略，结论如下：

（1） 无论是范围还是长度发生变化，儿童分别采取心理长度和比例判断等估計策略，表明对熟悉范围数字的认识已达到等距和等比水平。

（2） 即使实验条件相同0～100（10cm），儿童对中端数字的估计策略也受到不同情境的影响。

（3） 儿童会根据不同类型的复杂情境灵活地选择不同的估计策略，为重叠波理论提供了新的证据。

参考文献

曹碧华，曾春雲，廖虹，李富洪（2021）. 心理长度对二年级儿童数字线估计表征的影响. 心理发展与教育， 37（2），190-198.

刘国芳，辛自强（2012）. 数字线估计研究： “模型”背后的策略. 心理研究，5（2），27-33.

莫雷，周广东，温红博（2010）. 儿童数字估计中的心理长度. 心理学报，42（5），569-580.

邢强，徐争鸣，蔡新华（2015）. 小学生数字线估计中的分段策略. 数学教育学报，24（4），82-85.

臧蓓蕾，张俊（2017）. 基于潜在类别分析的方法探究3～5岁儿童心理数线发展的特点. 学前教育研究，12（7），49-60.

臧蓓蕾，张俊，顾荣芳（2019）. 幼儿心理数线的发展： 估计准确率与模式背后的策略. 心理与行为研究，17（6）， 795-802.

张帆，赖颖慧，陈英和（2015）. 儿童数字线表征的发展——心理长度的影响. 心理发展与教育，31（2），149-156.

张丽，卢彩芳，杨新荣（2014）. 3～6年级儿童整数数量表征与分数数量表征的关系. 心理发展与教育，30（1），1-8.

周广东，莫雷，温红博（2009）. 儿童数字估计的表征模式与发展. 心理发展与教育，25（4），21-29.

Ashcraft， M. H.， & Moore， A. M. （2012）. Cognitive pro-cesses of numerical estimation in children. Journal of Experimental Child Psychology， 111（2）， 246-267.

Barth， H. C.， & Paladino， A. M. （2011）. The development of numerical estimation： Evidence against a representational shift. Development Science， 14（1）， 125-135.

Booth， J. L.， & Siegler， R. S. （2006）. Developmental and individual differences in pure numerical estimation. Developmental Psychology， 42（1）， 189-201.

Case， R.， & Okamoto， Y. （1996）. The role of conceptual structures in the development of children's thought. Monographs of the Society for Research in Child Dev-elopment， 61（1）， 189-214.

Dehaene， S. （1997）. The number sense： How the mind cre-ates mathematics. New York：Oxford University Press.

Faul， F.， Erdfelder， E.， Lang， AG.， Buchner， A. （2007）. G*Power 3： A flexible statistical power analysis program for the social， behavioral， and biomedical sciences. Behavior Research Methods 39（2）， 175-191.

Geary， D. C.， （2011）. Consequences， characteristics， and causes of mathematical learning disabilities and persistent low achievement in mathematics. Journal of Developmental & Behavioral Pediatrics， 32（3）， 250-263.

Hollands， J.G.， &Dyre， B. （2000）. Bias in proportion judg-ments： the cyclical power model. Psychological Review， 107（3）， 500-524.

Joram， E.， Gabriele， A. J.， Bertheau， M.， Gelman， R.， & Subrahmanyam， K. （2005）. Childrens use of the refe-rence point strategy for measurement estimation. Journal for Research in Mathematics Education， 36（1）， 4-23.

Opfer， J. E.， Thompson， C. A.， & Kim， D. （2016）. Free ver-sus anchored numerical estimation： A unified approach. Cognition， 149， 11-17.

Peeters， D.， Degrande， T.， Ebersbach， M.， Verschaffel， L.， &Luwel， K. （2016）. Children's use of number line estimation strategies. European Journal of Psychology of Education， 31（2）， 117-134.

Rouder， J. N.， & Geary， D. C. （2014）. Children's cognitive representations of the mathematical number line. Dev-elopmental Science， 17（4）， 525-536.

Sella， F.， Berteletti， I.， Lucangeli， D.， &Zorzi， M. （2015）. Varieties of quantity estimation in children. Deve-lopmental Psychology， 51（6）， 758-770.

Siegler， R. S. （1996）. Emerging minds： The process of chan-ge in childrens thinking. New York： Oxford University Press.

Siegler， R. S.， & Booth， J. L. （2004）. Development of num-erical estimation in young children. Child Dev-elopment， 75（2）， 428-444.

Siegler， R. S.， &Opfer， J. E. （2003）. Thedevelopment of num-erical estimation： Evidence for multiple representations of numerical quantity. Psychological Science， 14（3）， 237-243.

Sietske， V. V.， Slot， E. M.， Kroesbergen， E. H.， Van'T， N.， &Leseman， P. （2013）. The added value of eye-tracking in diagnosing dyscalculia： A case study. Frontiers in Psychology， 4， 679.

Slusser， E.， & Barth， H. （2017）. Intuitive proportion judg-ment in number-line estimation： Converging evidence from multiple tasks. Journal of Experimental Child Psychology， 162， 181-198.

Spence， I. （1990）. Visual psychophysics of simple grap-hicalelements. Journal of Experimental Psychology： Human Perception and Performance， 16（4）， 683-692.

Sullivan， J.， &Barner， D. （2014）. The development of st-ructural analogy in number-line estimation. Journal of Experimental Child Psychology， 128， 171-189.

Wall， J. L.， Thompson， C. A.， Dunlosky， J.， & Merriman， W. E. （2016）. Children can accurately monitor and co-ntrol their number-line estimation performance. Deve-lopmental Psychology， 52（10）， 1493-1502.

Zang， B.， Zhang， J.， & Gu， R. （2019）. Chinesepreschoolers mental number line and mental number distance： valid characteristics using dirichlet process gaussian mixture model. Early Education and Development， 30（5）， 694-707.