“有理 有序 有创”让学生直面数学思维

林谢剑

一直以来，数学都以严谨的逻辑思维著称。作为一门基础性学科，数学教育不仅仅是要让学生掌握必需的数学基础知识与基本技能，更重要的是发展学生的抽象思维和推理能力。在课堂教学活动中，教师要融合新教学理念，优化教学设计，创新教学策略，让学生在运用知识解决问题的过程中直面数学思维。接下来，笔者就教学中如何有效激发学生直面数学思维、提高课堂教学效率，谈谈具体做法。

一、以前置练习为铺垫，直面数学思维的“有理性”

“理”即指理由、依据。如何让学生认识推理是有迹可寻的？在教学中，教师应该充分把握知识本身的内在逻辑性，在新知教学前巧设前置练习，以前置练习为脚手架，引发勾连，激发学生获取知识的内在需求。在数学教学活动中，只有让学生亲身尝试，才能充分体悟其中的内涵，让数学思维的生成实现“有理性”。

例如，在《表面涂色的正方体》一课教学中，旨在引导学生在通过观察找到将表面涂色的大正方体每条棱平均分成3、4、5份后，切成的小正方体涂色面的情况的基础上，比较不同涂色面的个数及位置特点，通过合情推理，进而得到将每条棱平均分成n份后，切成的小正方体不同涂色面的个数是本课的知识重点。笔者在认真研读文本和教参的基础上，结合学生的实际情况，设置了探索数字规律的前置练习：

通过这样的环节设置，让学生数形结合，在感受数字之间规律的同时正确表达规律，并能根据规律继续填写。这样一来，规律的表达在此提前进行渗透，分散了教学难点，为新知教学中让学生找准每条棱平均分成3/4/5份后不同涂色面小正方体的个数，并将之推广到n份后的情况，做好铺垫准备。

又如，在《图形的平移》一课教学中，旨在引导学生观察发现图形在平移过程中，整个图形的每一个部分都朝同一个方向移动，图形的平移实际上可以分解为对应点或者对应线的平移，这是本节课的重点。而本课的难点在于数对应点（线）之间的距离，在这一过程中，学生往往容易将起始点、终止点纳入思考范围，得到的距离比实际平移的距离多“1”或少“1”的情况。基于上述认识，笔者在课前设置了在格子图中数两个“点”、两条“线”之间距离的前置练习，让学生聚焦数距离，明确两点（线）之间的距离其实就是数它们之间的格子数。当从“点”的角度考虑，起始点表示还没开始移动，可用“0”来表示移动的距离，而后继续往下数。看似简单单一的知识，却很好地发展了学生的数学思维，起到了突破本课教学重点的作用，这样一来，数学思维的“有理性”便落到了实处。

二、以问题设计为导向，直面数学思维的“有序性”

“序”指顺序，万物生长都讲究循序渐进。在教学中，教师应当关注知识的内在生长，由易到难，层层推进，挖掘学生的最近发展区，引导学生拾阶而上，不断激发学生解决问题的热情。在数学教学活动中，只有让学生跳一跳摘苹果，才能更好地增强学生学习的兴趣，有利于学生获得学习的成就感。

例如，在《表面涂色的正方体》一课教学中，笔者设计了如下教学环节：

（一）初探平均分成3份。在新知教授环节，笔者通过动态展示将表面涂色的大正方体每条棱平均分成2份后切成的小正方体涂色面的情况，引导学生明确切成的2×2×2=6个小正方体均为3面涂色。接着让学生自主探究将大正方体每条棱平均分成3份的情况，并指出小正方体不同涂色面的位置特点。有了前面将表面涂色的大正方体每条棱平均分成2份后，切成的小正方体的涂色面情况的教学引导，这个过程的自主探究对学生而言是可实现的。学生通过观察很容易就得出3面涂色的小正方体有8个；2面涂色的有12个；1面涂色的有6个。而对于位置特点，学生存在困惑，笔者在教学实际中暂且搁置该问题。

（二）再探平均分成4/5份。笔者继续提问：如果将这个大正方体的每条棱平均分成4份、5份……切成的小正方体涂色面又会是什么结果呢？学生自主探究后再小组合作交流。由汇报结果看来，对于3面涂色的小正方体个数基本上每位同学都能清晰地得到正确的结果8个。但对于2面涂色和1面涂色的小正方体个数，多数学生无法正确表达。

（三）观察推理，规律呼之欲出。《论语》有云：“不愤不启，不悱不发。”说的是学生如果不是经过冥思苦想而又想不通时，就不去启发他；如果不是经过思考并有所体会，想说却说不出来时，就不去开导他。为此，在学生的困顿处，笔者通过课件分别呈现每条棱平均分成不同份数后的不同涂色面的图形，启发学生：不同涂色面的小正方体位置有什么特点？你能结合正方体的各部分组成要素说一说吗？有了适时的提示引导，学生自觉将目光转向正方体的组成要素：顶点、棱、面。很快就发现将大正方体每条棱平均分后，得到的小正方体3/2/1面涂色的位置分别在大正方体的顶点、棱的中间、面的中间。笔者提出问题：现在你能算出平均分成3/4/5份后3/2/1面涂色的小正方体个数了吗？学生独立计算后得到结果如下：平均分成3份时，3面涂色的小正方体有8个，2面涂色的有1×12=12个，1面涂色的有12×6=6个；平均分成4份时，3面涂色的小正方体有8个，2面涂色的有2×12=24个，1面涂色的有22×6=24个；平均分成5份时，3面涂色的小正方体有8个，2面涂色的有3×12=36个，1面涂色的有32×6=54个。

（四）歸纳推理，规律始发成型。追问：如果将大正方体每条棱平均分成6份、10份、100份……你还能算出不同涂色面小正方体的个数吗？学生自主探究、小组交流后明确平均分成n份，3面涂色的小正方体都是8个；2面涂色的有：（n-2）×12个；1面涂色的有：（n-2）2×6个。

这样的教学过程，以问题设计为引领，让学生明确探究方向，有助于捋清学生的思路。通过或启发、或提问、或点拨、或追问等形式，将学生的思维一步步推向关键处，很好地激发了学生的探究意识。由此，数学思维的“有序性”得以实现。

三、以问题情境为抓手，直面数学思维的“创造性”

“创”作为一种思辨力，是在感知的基础上形成的具有变通性，能举一而反三的优良品质。在教学中，教师应当以问题情境为抓手，拓宽知识广度，直指知识核心，让学生不仅知其然更知其所以然。这样才能进一步激发学生的探究欲望，拓展思维，发展智能，让学生感受数学的内在魅力，进而培养创新意识。

例如：在《探索三角形三边关系》一课教学中，学生通过动手围、动笔算的方法初步感知到能围成三角形的任意两边之和要大于第三条边，对于这一陈述性的知识绝大多数的学生都会描述、能识记，但在解决问题中却常常不如人意。为了让学生在感知知识的基础上进一步扩宽思维，笔者设计了如下问题情境：

将一根10cm长的小棒剪成三段，怎样剪一定能围成三角形？（要求：剪成的每一段都是整厘米数。）

（1）第一刀不能剪在哪里？为什么？

（2）第二刀不能剪哪一段？为什么？

（3）如果第一刀剪在“3”处，第二刀应在（    ）处剪，剪成的三段保证能围成一个三角形。

由问题（1）指向两边之和等于第三边则围不成三角形，到问题（2）指向任意两边之和要大于第三条边，因此不能剪短的那一段的粗略判断，再到问题（3）第一刀剪在“3”，第二刀只能剪在“6”或“7”，得到三边长度分别为3、3、4的具体剪法，让学生再次经历推理，使其思维进一步走向深刻，同时正、逆向思维的不同思考方式也有效激发了学生推理的创造性表达，再现了数学思维的严谨性。

又如，在《多边形的内角和》一课的教学中，大多数教师设计如下教学环节：将四边形、五边形、六边形从一个顶点出发，分割成2、3、4个三角形，再由三角形的内角和为180°，推理得到四、五、六边形的内角和为180°×2，180°×3，180°×4，接着引导学生观察发现多边形的边数与分割成的三角形的个数之间相差2的关系，由此推出当多边形边数为n时，分割成的三角形个数为（n-2），则其内角和为180°×（n-2）。乍一看，该教学环节思路清晰、条理清楚、推理也是毫无破绽，但仔细思考，我们不难发现，该教学环节从一开始就先入为主了，我们不免疑惑：为什么要“从一个顶点出发分割三角形”？如果不是，结论难道就不成立吗？带着这样的思考，笔者设计了如下问题情境：

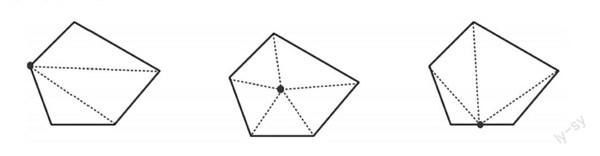
在探究五边形的内角和时，笑笑、奇思和妙想三位同学分别从不同角度将五边形分割成如下三角形，你赞同谁的做法？说说你的理由。

从学生的答题情况来看，近70%都赞同笑笑的做法，并且认为奇思和妙想的做法沒有“从五边形的一个顶点出发分割三角形”，是错误的，其实不然。奇思从五边形的内部找到一个点，将五边形分成5个三角形，这一过程产生内部多出来的5个角（刚好围成一个周角360°），由此得到五边形的内角和为180°×5-360°；妙想从五边形的边上找到一个点，将五边形分成4个三角形，这一过程产生内部多出来的4个角（刚好围成一个平角180°），由此得到五边形的内角和为180°×4-180°。因此三位同学的做法都是正确的。

这样的问题情境不再局限于知识点本身，拓宽了思维广度，直指知识核心，让学生在思辨中习得知识，不仅有利于激发孩子的探究欲望，拓展思维，发展智能，更能让学生感受数学的内在魅力，久而久之，数学思维的“创造性”就会得到进一步的培养。

总之，数学思维能力的培养需要教师的精心呵护，只有精准把握知识之间的前联后结，巧设问题，依托情境才能更好地让学生直面数学思维的“理”“序”“创”，从而有效助推学生的学习，让学习变得轻松愉悦，让学生会学、爱学、乐学。