GPS卫星可视性研究
高建东 邢尹
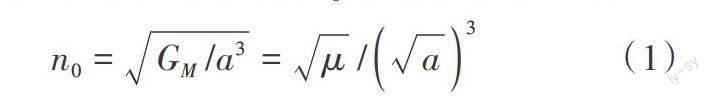

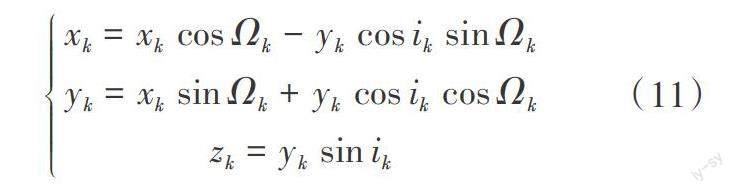
摘 要:【目的】研究相对于地面观测点的GPS卫星星座的可视性,从而改善观测数据质量,提高测量精度。【方法】本研究基于标准RINEX数据,通过假设卫星开普勒参数,拟定地面观测点及观测时间,并根据全球导航卫星系统定位原理来计算各GPS卫星坐标及相对于地面观测点的高度角,从而筛选出符合观测条件的GPS卫星。【结果】在计算出坐标及相对于地面观测点的方位角和高度角的24颗GPS卫星中,选出7颗高度角大于15°的卫星作为有效的观测卫星。【结论】本研究所述的方法可按照一定原则对GPS卫星星座进行筛选,从而获取质量更佳的卫星观测数据,为相关研究提供参考。
關键词:GPS;RINEX;卫星可视性;卫星高度角
中图分类号:P228 文献标志码:A 文章编号:1003-5168(2023)06-0018-05
DOI:10.19968/j.cnki.hnkj.1003-5168.2023.06.003
Research on Visibility of GPS Satellite
GAO Jiandong1 XING Yin2
(1. Jiangsu Institute of Surveying and Mapping Engineering, Nanjing 210013, China; 2. School of Geographic Science and Surveying Engineering, Suzhou University of Science and Technology, Suzhou 215009, China)
Abstract: [Purposes] This paper study the visibility of GPS satellite constellation relative to ground observation points, so as to improve the quality of observation data and improve the measurement accuracy.[Methods] In this study, based on the standard RINEX data and by assuming the Kepler parameters of the satellite, the ground observation points and observation time are proposed, and the GPS satellite coordinates and the elevation angle relative to the ground observation points are calculated according to the positioning principle of the global navigation satellite system, so as to select the GPS satellite that meets the observation conditions. [Findings] In accordance with the coordinates of 24 GPS satellites and the azimuth and elevation angles relative to the ground observation points, 7 satellites with an elevation angle greater than 15° are selected as effective observation satellites. [Conclusions] The method described in this study can sift the GPS satellite constellation according to certain principles, so as to obtain better quality satellite observation data and provide reference for related research.
Keywords: GPS; RINEX; satellite visibility; satellite altitude angle
0 引言
全球导航卫星系统(Global Navigation Satellite System,GNSS)是可为地球用户或空间用户提供定位和授时信息的卫星星座[1],其在很大程度上能反映一个国家的综合科技实力水平,是衡量一个国家科技发展的重要指标。全球定位系统(GPS)是美国在二十世纪七十年代开始建设的、世界上第一个用于导航定位的全球系统,经过几十年的不断发展和更新,目前GPS已成为全球星座组网最完善、定位精度最高、用户数量最多的卫星导航系统[2]。
在利用GNSS来进行控制测量时,导航卫星的分布状态、高度角等都会影响测量精度。根据观测点的位置,计算并预测卫星的高度角、方位角,从而筛选出有效的观测卫星,能有效改善观测数据的质量,极大提高GPS卫星对地面测量的精度。随着卫星导航技术的快速发展,对各类卫星的方位角和高度角的计算也越来越重要。
在卫星可视性分析领域中,国内外相关学者已进行非常深入的研究。早在2000年,西安测绘研究所的贾小林教授就对卫星对地的可视性进行研究,其对卫星系统的可用性及如何计算进行详细论述。2007年10月“嫦娥一号”成功发射后,李晓杰等[3]就发表了《环月卫星可见时段的计算和分析》,详细深入地解释了可见时段的计算原理,并根据地面站的布设方式的不同,采用不同的方法计算。除此之外,2013年魏东岩等[4]在第四届中国卫星导航学术年会上发表了《针对高轨平台的GNSS卫星可视性分析研究》,根据高轨平台的定位需求,从多种角度出发,对卫星信号的可视性进行分析。
1 卫星的可视性分析原理
1.1 标准RINEX格式
由于生产厂家的不同,导致GPS卫星接收到的数据在格式上存在巨大的差异,从而使数据处理较为困难。为了对GPS卫星接收数据的格式进行统一,瑞士伯尔尼大学天文学院的Gurtner于1989年提出Receiver Independent Exchange Format(RINEX)[5]。之后,所有的卫星数据便能以统一的形式呈现在世人的面前,方便对各种型号接收机的数据进行综合处理,极大提高工作效率。RINEX文件是一个统一的格式文件,其包含了卫星观测数据的文件、导航电文文件和气象数据文件[6]。其中,导航电文是RINEX文件中负责保存GPS星历信息的文件,且轨道参数、星历参考时刻、钟差改正数及摄动改正数都存放在RINEX文件中。
1.2 卫星坐标计算
导航电文包含卫星某时刻的具体空间位置信息[7],从中读取所需的参数,再通过以下计算流程,就能得到卫星的坐标。
1.2.1 解算卫星运行的平均角速度n0。由开普勒第三定律可知,平均角速度n0的计算公式见式(1)。
式中:G为重力常数;在WGS-84坐标系中,μ为地球的引力常数,μ=3.986 005×1014 m3/s2。
卫星的平均角速度n通常为n0与摄动改正数Δn之和,计算公式见式(2)。
1.2.2 解算归化时间tk。卫星轨道参数受参考时刻的影响,其会随着选择时刻的改变而发生变化。先求出参考时刻与观测时刻的差值,从而得到归化时间tk。观测时刻卫星瞬时的平近点角Mk的计算见式(3)。
式中:M0为参考时刻的平近点角;tk为归化时间。
根据公式(3)可求出平近点角Mk。偏近点角Ek的计算见式(4)。
可利用迭代法来求出偏近点角Ek,使[Ek=Mk],求出Ek,再代入即可求出Mk。
根据公式(4)中偏近点角Ek,可计算出真近点角Vk,其计算见式(5)。
根据公式(5)算出的真近点角Vk,升交距角Φk的计算见式(6)。
式中:ω为近地点角距。
对摄动改正项进行求解,计算公式见式(7)。
式中:δu为升交距角u的摄动量;δr为矢径r的摄动量;δi为倾角i的摄动量。
对改正后的升交距角uk、rk、ik进行计算,见式(8)。
对卫星在轨道平面坐标系的坐标进行计算,见式(9)。
根据公式(8)和公式(9)计算出的结果,可算出观测时刻升交点精度Ωk,计算公式见式(10)。
式中:ωe为地球自转速率,ωe=7.292 115 67×10-5 rad/s;Ω为升交点对时间的变化率。
1.2.3 卫星坐标计算。根据公式(10)的计算结果,可计算出卫星在WGS-84坐标系中的坐标。对轨道平面坐标系中的坐标进行变换,就能得到在WGS-84坐标系中的坐标,见式(11)。
经过以上步骤的计算,可得到卫星在某时刻的具体空间坐标。
2 实例及分析
2.1 参数计算
在对卫星的位置坐标进行计算前,要拟定好24颗卫星的开普勒参数。首先要计算出卫星运行的平均角速度,在对坐标进行计算时,有一个非常重要的步骤,即卫星归化时间的计算,采用之前已拟定好的时刻(2021年4月29日4时0分0秒),将时间系统统一后再进行计算,在转化好时间后,可计算出每个卫星的平近点角和偏近点角,要注意的是,偏近点角要进行迭代计算。在此之后,还要计算出地心矢径、真近点角、升交点角距、倾角,最后可通过已知的公式计算得到卫星在轨道坐标系中的坐标,并通过转换得到其在WGS-84大地坐标系中的坐标。
当得到卫星在WGS-84坐标系中的坐标后,拟定观测点的地心坐标为(3 757 014 m,980 682 m,6 378 137 m),经过转换后,得到的经度为119.190 042 494°、纬度为33.830 618 060°。然后利用已知的测站坐标和24颗卫星的地心坐标,将卫星的地心坐标通过计算公式转换成站心坐标,在求出各卫星的站心坐标后,可计算出卫星的方位角和高度角。
2.2 计算实例及分析
为了计算出卫星的坐标,要利用到开普勒参数,拟定的开普勒参数见表1。
在表1给出的开普勒参数基础上,计算得到卫星在轨道平面内的坐标,结果见表2。
经过计算公式的转换,可得到卫星在WGS-84大地坐标系中的坐标,结果见表3。
由于拟定观测点的地心坐标为(3 757 014 m,980 682 m,6 378 137 m),所以转换后的经纬度为(119.190 042 494°,33.830 618 060°)。可计算得到每个卫星相对于观测点的方位角与高度角,见表4。
因为卫星的高度角会直接影响到卫星的观测范围及相应的观测精度,所以在计算得到卫星的方位角和高度角后,可从中选出高度角大于15°的卫星,将其作为有效观测卫星,而选出的有效观测卫星能使测量得到的数据更有参考意义。高度角大于15°的卫星见表5。
由表5可知,高度角大于15°的卫星一共有7颗,在测量时可选取这7颗卫星作为参考,这样从中提取到的数据误差比别的卫星要小,比通过其他卫星得到的数据具有更高的精确性和可靠性。
3 结语
本研究基于全球导航系统基本原理,并给出卫星坐标的计算方法。根据假定地面观测点坐标计算出GPS星座卫星的高度角,从而筛选出高度角大于15°的7颗卫星数据,并获取质量更佳的卫星观测数据,为相关研究提供参考。本研究的试验计算并未考虑摄动参数的影响,计算出的高度角与真实情况存在着细微差异。在今后的研究中,可考虑加入卫星的摄动及各种改动参数,从而设计出更加符合实际情况的试验验证,并采用其他全球导航卫星系统(如俄罗斯的Glonass、欧洲的Galileo及中国的北斗卫星导航系统)数据进行计算验证,从而确保获取到更全面、准确的导航卫星可用性信息。
参考文献:
[1]王琦.全球定位系统(GPS)的原理與应用[J].卫星与网络,2010(4):26-30.
[2]赵洪岩,顾永智,尹利军.GPS全球定位系统的应用[J].河南科技,2011(6):34.
[3]李晓杰,郑勇.环月卫星可见时段的计算和分析[J].测绘科学,2009(3):58-60.
[4]魏东岩,袁洪,李亮,等.针对高轨平台的GNSS卫星可视性分析研究[C]//第四届中国卫星导航学术年会,2013:126-130.
[5]GURTNER W.RINEX-The Receiver Independent Exchange Format-Version 3.00[J]. Gps World,2007(7):48-52.
[6]冯胜涛,刘志广,占伟,等.RINEX观测数据文件格式及其应用[J].华北地震科学,2014(1):38-46.
[7]王猛,张志伟.利用广播星历计算卫星的瞬时坐标[J].城市勘测,2010(2):88-90,93.

