基于多维尺度特征增强的公路结构层无损检测识别方法
孟利强, 周丽军
(山西省智慧交通研究院有限公司 智慧交通山西省实验室, 山西 太原 030032)
0 引 言
随着公路运营时间的增加, 公路路基结构层会发生空洞、脱空、裂缝、疏松、塌陷等病害[1], 特别是公路塌陷严重威胁着人民的生命财产安全。传统的检测技术, 如岩心钻孔法和其他破坏性检测方法的样品数量有限, 且测试成本昂贵、耗时, 不能保证实时获得检测结果, 在路面上钻孔的行为也会对道路结构造成不可逆转的破坏[2]。探地雷达(GPR)是一种无损性电磁检测技术, 因其非破坏性、高效、连续检测和直观图像的特点而被广泛应用于地下结构物检测。根据不同地下目标介质的电磁特性(如介电常数、电导率、渗透率等), 能获得不同的电磁散射回波, 当地下介质的电磁特性发生变化时, 电磁波将相应地产生反射和折射回波。通过对接收机接收到的回波进行处理和分析, 可以根据回波、位置、结构、几何形状等信息的波形、强度、回波时间等, 推断出地下目标的情况。
城市道路的地下结构物通常有排水排污管道、电力管道等, 随着道路运营时间的增加会产生空洞、脱空等病害。高速公路的地下结构物通常有排水管道、涵洞、混凝土钢筋网等, 也存在层间脱空、不密实等病害[3-4]。尽管GPR采集数据的效率较高, 但是, 因雷达分辨率的影响以及地下结构物先验知识的缺乏, 对公路结构物的解析依旧是难点问题。
常用的探地雷达数据处理方法有基于图像的信号处理方法, 即将检测回波数据导出为图像, 对图像中的像素值进行处理。处理过程通常包括修正对比度、亮度、锐化边缘或降噪, 而这一过程是基于全幅图像进行处理的, 不利于提取弱能量目标[5]。探地雷达数据中有全局直达波与层间回波, 利用全局图像处理尽管消除了直达波, 但也同时消除了层间回波, 无法得到地下各层间的信息。为了能同时获取强能量目标与弱能量目标, 有的研究利用小波分析来进行雷达图像处理。文献[6]从GPR图像中定位隐藏的目标, 该方法所采用的是一种基于小波分析的降噪方法, 首先利用感兴趣区域(ROI)区分埋藏对象, 然后利用Hough变换在高频分量与低频分量上检测目标。从高低频分量能区分目标与背景直达波等干扰, 但探地雷达电磁散射回波数据中的管道与空洞等目标呈现的频率均为高频信息, 因此, 对于目标信息之间的差异还需从其它维度进一步分析。
考虑到探地雷达回波不仅包含不同目标的高低频信息, 在地下背景与有界目标之间还存在方向性差异, 因此, 使用了二维Gabor变换, Gabor变换基于Gabor滤波器, 它对纹理、边缘等特征较为敏感, 尤其是能提供局部空间的细节信息, 具有较好的方向选择和尺度选择特性, 在图像处理、模式识别等领域得到了广泛的应用[7]。本文充分利用了Gabor变换的频率和方向特性对于纹理的表征, 从频域的不同尺度、不同方向上提取相关特征来对雷达图像进行解释, 并以两段路的结构层为例进行了算法分析。
1 Gabor滤波尺度变换
在二维图像空间(x,y)中, Gabor滤波器是高斯核函数与正弦平面波的乘积, 具体表示为[8]
g(x,y;λ,θ,φ,σ,γ)=
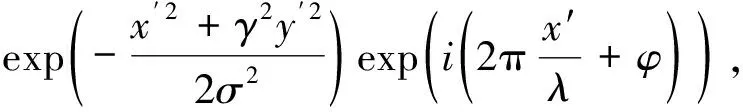
(1)
式中:x′=xcosθ+ysinθ,y′=-xsinθ+ycosθ;λ为正弦函数的波长, 单位为像素, 通常有2≤λ≤min(P,Q)/5,P,Q为输入二维图像的尺寸;θ为Gabor核函数的方向;φ为相位偏移, 且φ∈[-π,π];σ为高斯函数的标准差;γ为空间纵横比, 表征了Gabor函数在形状上的椭圆率。
图1 为波长尺度为[2 m,5 m,8 m,10 m], 方向为[10°,45°,60°,90°]参数下的Gabor滤波的实部与虚部图。
由图1 可以看出, 在不同波长尺度下, Gabor滤波器中出现了不同宽窄与纹理的明暗条纹。改变滤波器方向参数, Gabor滤波器中的明暗条纹会呈现不同的方向趋势。将上述滤波器与图像进行卷积计算, 那么图像中纹理频率与滤波器的频率越接近, 其纹理增强作用就越强, 反之会越弱。因此, 根据检测图像中待检目标的方位趋势, 选择合适的方向参数进行滤波, 可以更加突出目标特征。从图1 中还可以看出, 当波长变化时, 明暗条纹的像素点信息发生了变化, 随着波长的增加, 明暗条纹越趋平滑, 反之明暗条纹呈现出明显的像素级信息。
2 多维尺度变换的频率与方向性特征分析
Gabor变换体现了良好的多频率局部性与多分辨率特性, 如果对图像进行多维尺度滤波, 那么每个维度都将得到特定特征的局部信息, 这样就可以根据需要在不同尺度上分析图像[9]。通过在不同尺度方向的Gabor滤波可以进一步增强边缘以及峰、谷、脊轮廓等底层图像特征。那么, 待处理图像Ii(x,y)经过滤波后的图像为[10]
I(x,y,λ,θ,φ,σ,γ)=
Ii(x,y)*g(x,y,λ,θ,φ,σ,γ),
(2)
也就是利用Gabor滤波器核函数对待处理图像进行卷积运算, 可以得到提取的特征图像。
通过调整Gabor滤波器的参数, 能得到不同参数下的滤波图像, 考虑到探地雷达检测回波时对频率和极化方向(即方向性)较敏感, 因此, 本文主要分析Gabor滤波中的频率与方向特征。这里, 实际频率f′=c/λ,c为光速,λ为波长, 将实际频率按照光速归一化, 得到频率f=1/λ; 方向θ=nπ/N,n表示第n个方向,N表示方向特征总数。以下从两个例子分析Gabor变换的频率与方向性特征对图像的影响。
图2 为待检测原图与归一化频率f=0.1, 方向角度为[0°,30°,90°,135°]的Gabor变换的图像增强图。在f=0.1、方向角度为0时, 方向特征为垂直特征, 此时图2(a)垂直方向纹理的增强见图2(b); 在f=0.1、方向角度为30°时, 图2(a)沿30°方向的斜纹理特征的增强见图2(c); 在f=0.1、方向角度为90°时, 图2(a)沿90°方向即水平方向的纹理特征的增强见图2(d); 在f=0.1、方向角度为135°时, 图2(a)沿135°方向的纹理特征即向右下方倾斜特征的增强见图2(e)。

图2 归一化频率f=0.1和方向角度为[0°,30°,90°,135°]的Gabor变换的图像增强
图3 为归一化频率f=0.4, 方向角度为[0°,30°,90°,135°]的Gabor变换的图像增强图。由图3 可以看出, 在与图2 相同的方向角度下, 增加归一化频率, 整体图像细节信息增强。相比图2(b), 图3(a)中在方向角度为0°时的垂直细节信息随着频率的增加而增强。在方向角度为30°时沿此方向的方格内线条的增强见图3(b); 在方向角度为90°时水平方向细节信息的增强见图3(c); 在方向角度为135°时沿此方向的线条信息的增强见图3(d)。

图3 归一化频率f=0.4和方向角度为[0°,30°,90°,135°]的Gabor变换的图像增强
3 实测分析
3.1 地下管道弱回波测试
以某段路的探地雷达测试为例分析所提出方法的应用效果。路段下方有3根市政管道, 路面无明显破损, 探地雷达中心频率为750 MHz。图4 为实测场景的测量方式示意图, 图5 为探地雷达检测回波的原始图像。从图5 可以看出, 采集到的原始回波图像包含了强能量反射直达波, 直达波下方的(9 ns, 7 m)处能直观看见异常, 直达波下方的(19 ns, 11.5 m)处能直观看到管道的双曲线回波。
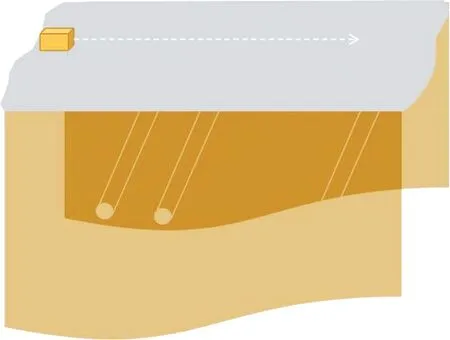
图4 实测场景示意图
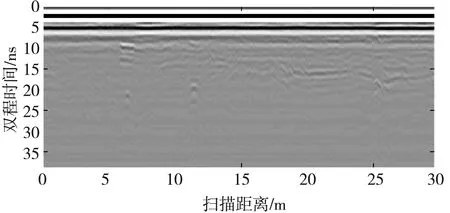
图5 探测雷达检测回波原始图像
图6 为对原始图像图5 去除直达波后的增强图。从图6 可以看出, 去除直达波后增强了直达波下方的回波信息。通过分析GPR图像中异常区域的共同特征, 可以得出异常区域有明显的反射能量, 其亮度明显高于背景。异常区域还具有杂乱的波形特征和明显的方向性特征。在(20 ns, 7 m)处有明显的平顶双曲线, 可判定为管道。

图6 去除直达波后的增强图像
图7 为归一化带宽为0.35, 方位为0.3 rad, 归一化频率为2, 角度为90°的滤波器实部、频率-波速图与变换后的图。
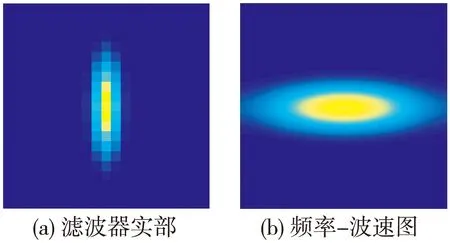
(c)经Gabor变换的回波增强图像
从图7 可以看出, 此参数下的Gabor变换滤波器实部呈竖条状, 能量居中最高, 并呈对称减弱, 见图7(a); 频率-波速图中能量居中最高, 见图7(b); 在此滤波器下得到的Gabor变换图像增强了垂直方向的回波信息, 见图7(c)。对比图6与图7(c), 在(19 ns, 25 m)处有明显的增强回波(如图中方框所示), 而这条管道在图5 的原始回波图像中不明显。
图8 为归一化带宽为0.65, 方位为0.4rad, 归一化频率为0.7, 角度为90°的滤波器实部、频率-波速图与变换后的图。
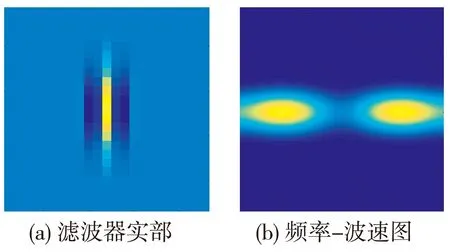
(c)经Gabor变换的回波增强图像
从图8 可以看出, 此参数下的Gabor变换滤波器实部呈竖条状, 能量居中最高, 两边能量呈对称减弱, 见图8(a), 滤波器频率-波速图为同一频率下的两块高能量波速, 见图8(b), 在此滤波器下得到的变换图像见图8(c)。从图8(c)可以看出, 此参数下的滤波器能较好地体现原图像中的异常, 使得回波中地表面回波、层之间的回波较强, 管道双曲线回波中横向部分较强。需要特别注意的是用此参数滤波获得了(9 ns, 8 m)处的异常(如图8(c)中方框所示), 而此处的异常在原始图像中仅有微弱呈现。
图9 为不同Gabor滤波器带宽、方位、波长、角度参数下得到的不同回波增强图。从图9 可以看出, 在方向0°下能明显增强水平方向信息, 见图9(a), 图9(a)方框中层间水平回波增强, 并且抑制了其它分量回波; 在方向90°下显示出明显的纵向波形信息, 见图9(b), 图中方框内标识出的增强的管道呈现出双曲线波形; 在图9(b)的基础上减小波长, 可以得到更清晰的层间信息, 见图9(c), 从图9(c)标识的方框内目标可以看出, 波长减小后分辨率更高, 因此, 层间信息更清晰; 图9(d)给出的参数抑制了水平与纵向信息, 突出显示了双曲线信息, 从图9(d)方框中能明显看到3根管道呈现的双曲线波形; 在图9(d)参数的基础上增加带宽, 在增强管道双曲线波形的同时也增强了(15 ns,19 m)处的异常信息, 见图9(e)与图9(f), 并且从图9(f)全局来看, 整体上抑制了水平信息, 突出了地下异常信息。相比图6 中的3处检测结果, 在方向参数为90°时漏检率降低了25%。
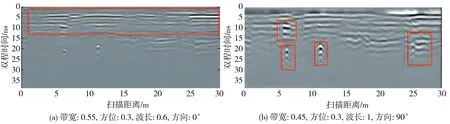
图9 不同参数Gabor变换的回波增强图像
3.2 弱回波异常检测测试
使用探地雷达对某路段进行检测, 中心频率为600 MHz, 其中, 一处路面有1个窨井盖, 路面无明显破损。图10 为实测场景的测量方式示意图, 图11 为探地雷达检测回波的原始图像。
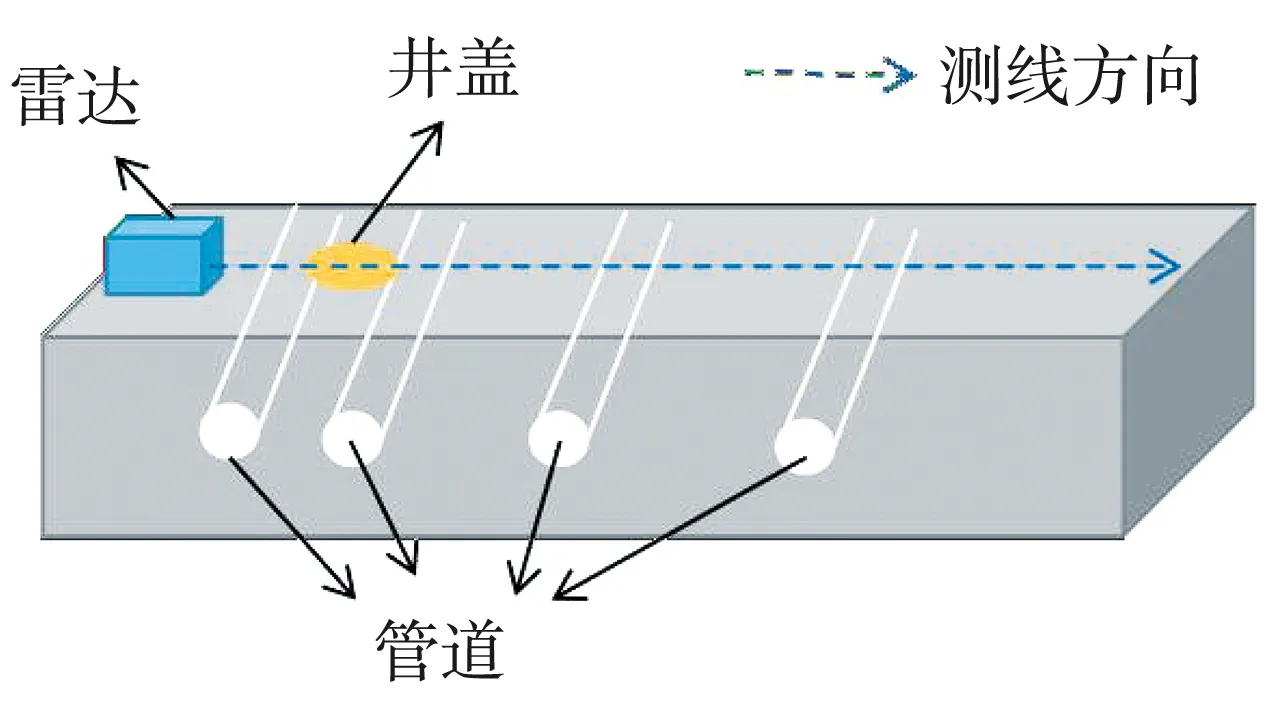
图10 实测场景示意图
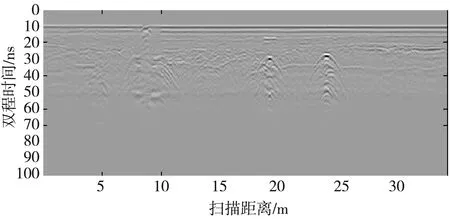
图11 探测雷达检测回波原始图像
通过分析图11 中异常区域的共同特征可以得出, 异常区域有明显的能量反射, 其亮度明显高于背景亮度。异常区域还具有杂乱的波形特征和明显的方向性特征。从图11 还可以看出, 在约(10 ns,9 m)处有明显的平顶双曲线呈现(双曲线中间有一定宽度), 结合双曲线顶点与其下方的多次回波能判定此处为窨井盖, 在大约(25 ns,19 m)与(26 ns,24 m)处有明显的双曲线回波, 可判定为管道。
图12 为归一化带宽为1.15, 方位为0.3 rad, 归一化频率为0.8, 角度为90°参数下的回波增强图。从图12 中可以看出, 经过以上参数的Gabor变换可以增强垂直方向的回波信息, 对比图12 与图11, 在约9 m, 10 ns~60 ns处有明显的增强回波, 且在窨井盖的两侧可以看见明显的管道回波, 可以估算管道处于约30 ns的时间深度, 而这2条管道在图11 的原始回波图像中不明显。经过滤波增强后, 在19 m与24 m处的管道回波更加明显, 不仅能呈现管道顶端的回波, 还能突出管道底端的回波。

图12 参数(1.15,0.3,0.8,90°)的回波增强图像
图13 为归一化带宽为0.45, 方位为0.3 rad, 归一化频率为0.7, 角度为180°参数下的回波增强图。
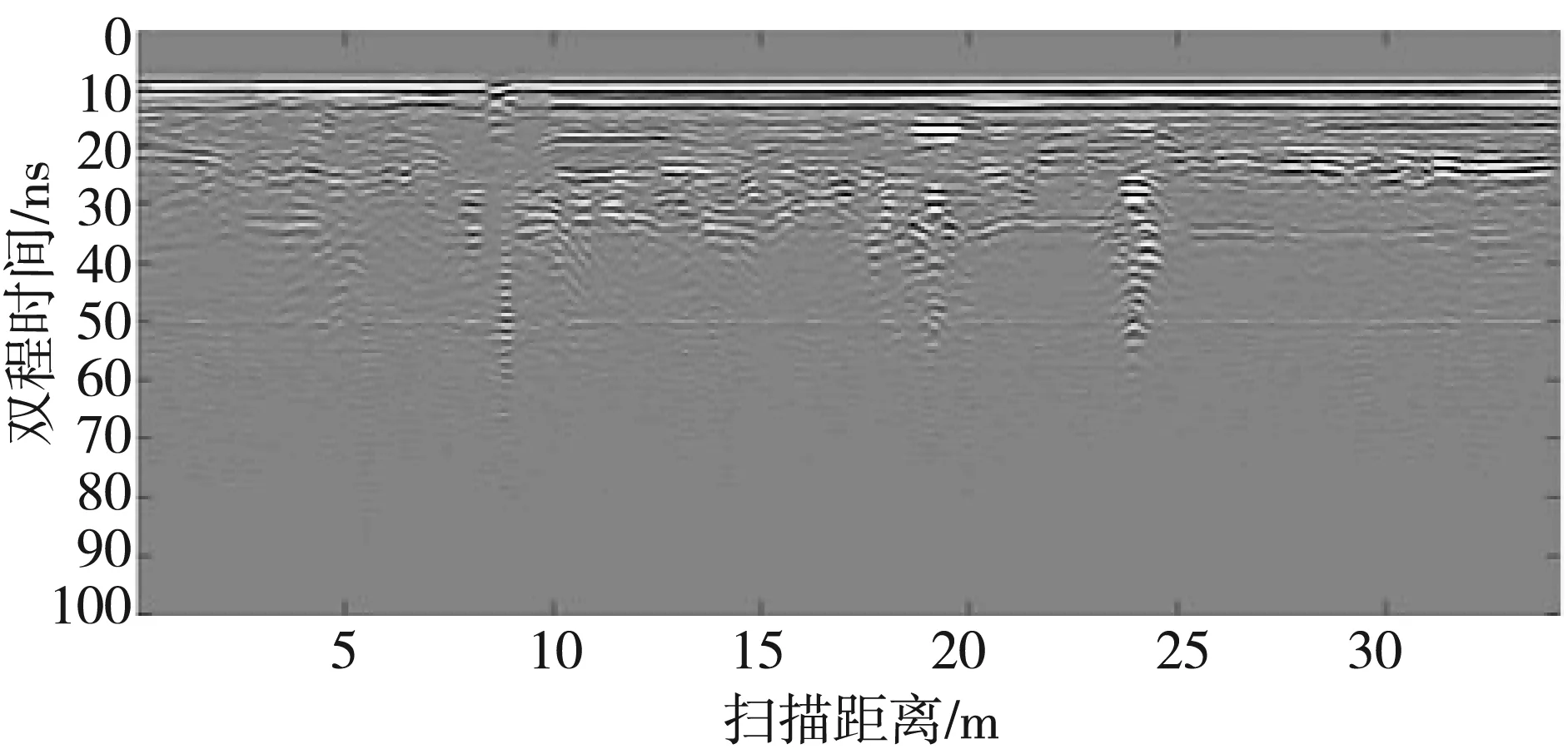
图13 参数(0.45,0.3,0.7,180°)的回波增强图像
从图13 可以看出, 此参数下的滤波器能较好地体现图11 中的横向波形分量, 抑制了纵向波形分量, 使得回波中地表面回波、层之间的回波较强, 管道双曲线回波中横向部分较强。需要特别注意的是, 用此参数滤波获得了(15 ns,19 m)处的异常, 而此处的异常在原始图像中有微弱呈现。因此, 相比图11 中的3处目标, 在参数为(0.45,0.3,0.7,180°)时能够提取管道上方异常, 漏检率降低了25%。
4 结 论
由于地下结构物所在背景环境的复杂性, 使得探地雷达采集的回波数据受到杂波干扰, 容易忽略弱能量目标。本文通过研究探地雷达对地下目标探测的回波信息中所包含的高低频率信息、地下背景与有界目标之间的方向性差异等, 调整二维Gabor变换的带宽、方位、波长、角度等参数, 从频域及方向的相关特征对探地雷达回波进行弱能量目标提取。通过实测的地下管道回波分析, 在方向参数90°时, 提取了弱回波管道信息, 目标漏检率降低了25%; 通过对地下管道附近异常的实测数据分析, 在归一化带宽为0.45, 方位为0.3 rad, 归一化频率为0.7, 角度为180°参数时提取了管道上方的异常信息, 目标漏检率降低了25%。

