基于扩展卡尔曼滤波的无人机航姿算法
赵嘉梁, 李世中, 赵紫良
(中北大学 机电工程学院, 山西 太原 030051)
0 引 言
近年来, 无人机被广泛应用于航空侦察、立体地图重构、搜救等方面。其中, 姿态航向参考系统(Attitude and Heading Reference System, AHRS)解算的精度和速度关乎到无人机操控计算的稳定性、可信度和实现的难度, 它可以提供载体俯仰角θ、横滚角φ和航向角ψ的信息, 是无人机飞行控制的先决条件[1-2]。
国内外已有不少学者在无人机航姿算法方面进行了大量研究, 文献[3]提出了一种基于卡尔曼滤波求解姿态的方法, 它是将具有信噪比的多种信号加以集成的线性最小方差预测技术, 在建模时需要考虑噪音的干扰, 然而在现实应用中, 由于小型无人机航姿模型为非线性, 此时卡尔曼滤波算法对其的错误处理会使航姿解算准确度下降, 甚至发散。文献[4]中提出了四元数卡尔曼滤波器, 但未提供传感器和硬件设计信息, 也未在工程上实现。文献[5]提出的微机械捷联式AHRS的四元数卡尔曼滤波器具有较高的静态精度, 但未考虑加速度对航姿解算的影响, 具有一定的局限性。文献[6-7]均采用了四元数卡尔曼滤波方法, 但四元数协方差阵出现奇异, 导致发散, 且此问题未被解决。
本文主要对小型无人机航姿算法进行研究, 提出的AEKF(Adaptive Extended Kalman Filter)算法可有效解决上述问题, 且经三轴转台实验测试结果表明此算法可以提高无人机的航姿解算精度。
1 航姿系统工作原理
首先采集陀螺仪角速度信息, 将信号进行预处理后更新姿态角[8-9], 然后利用加速度计解算俯仰角θ、横滚角φ。
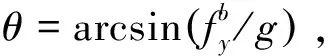
(1)
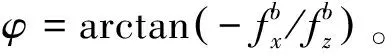
(2)
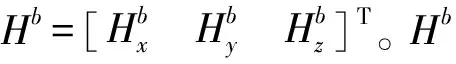
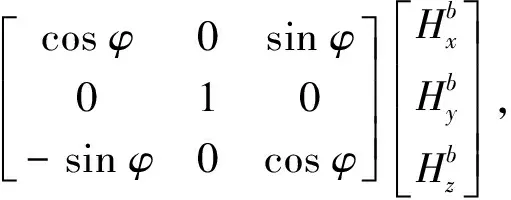
(3)

(4)
ψM为磁航向角,α为当地磁偏角, 则载体航向角为ψ=ψM±α。
系统总体流程如图1 所示。

图1 航姿系统总体流程
2 EKF算法及改进
2.1 EKF算法理论
为适应卡尔曼滤波的实际应用需求, 处理非线性系统的滤波问题, EKF需要将当前状态量与协方差线性化[10-12]。非线性系统状态向量为x∈Rn, 状态方程[13]为
xk=f(xk-1,uk-1,wk-1)。
(5)
测量向量为z∈Rm满足测量方程
Zk=h(xk,vk),
(6)
式中:xk和xk-1分别表示k和k-1时刻的状态量;uk-1为外界输入;h表示k时刻xk与Zk之间的关系;wk表示过程噪声,vk表示测量噪声, 令它们相互独立且满足正态分布:p(w)~N(0,Q),p(v)~N(0,R),Q、R为噪声协方差, 假设它们恒定。实际过程中, 随机变量wk和vk为未知量, 假定其数值为0, 则状态向量和测量向量的估计值为

(7)

(8)

线性化状态方程和测量方程[14]为

(9)

(10)
式中:A,W分别为f对x,w偏导的雅可比矩阵。H,V分别为h对x,v偏导的雅可比矩阵。
预估误差与观测误差分别为
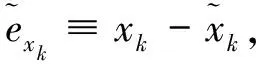
(11)

(12)
误差的表达式可表示为

(13)

(14)
式中:εk和ηk表示均值为0的独立随机变量。
利用一次离散卡尔曼滤波算法, 对误差估计矢量进行后验估计, 可得

(15)
则卡尔曼滤波的表达式为
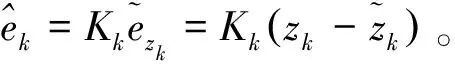
(16)


(17)
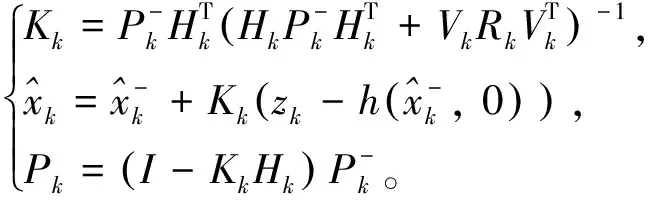
(18)
2.2 EKF模型的构建
构建无人机航姿系统的EKF数学模型, 其状态方程[15]为
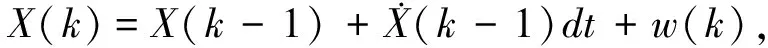
(19)

把式(3)代入式(19)中, 不计噪声项, 展开得到

(20)
通过式(1), 式(2)和式(4), 从加速度计和磁传感器的数据中计算出量测向量
Z(k)=X(k)+v(k),
(21)
式中:v(k)表示量测噪声。根据式(9)和式(10), 取定初始值并优化相应滤波参数, 按式(17)和式(18)进行迭代运算。
2.3 EKF算法改进
当实际应用环境中存在瞬变磁干扰时, 量测航向误差较大, 卡尔曼滤波无法迅速减少这种误差, 导致滤波发散[16-17]。自适应EKF算法(AEKF)主要用于解决此类问题, 其基本原理如下:
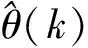
具体用以下公式表达
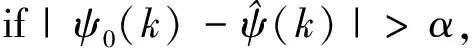
(22)
R=α*R0,
(23)

(24)
式中:R为观测噪声矩阵,R0为矩阵初始值。
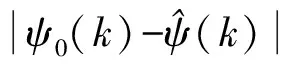
3 实验结果及分析
实验使用的主控芯片采用STM32F103, MEMS传感器为GY953, 其内部集成了加速度计、陀螺仪及磁力计, 精度高且稳定性好。
本文分别通过静态恒定、动态变化及瞬变磁干扰3种实验, 验证EKF及其改进算法的性能。
3.1 静态恒定实验
将无人机航姿系统置于转台, 对转台3个轴的角度进行调节, 并对θ,φ,ψ3个姿态角误差依次进行评估, 具体如下:
1)将转台维持为θ与φ示值相同的状态, 当转台处于-60°,-30°, 0°, 30°和 60°时保持静态恒定, 得到θ和φ的误差如图2 所示。
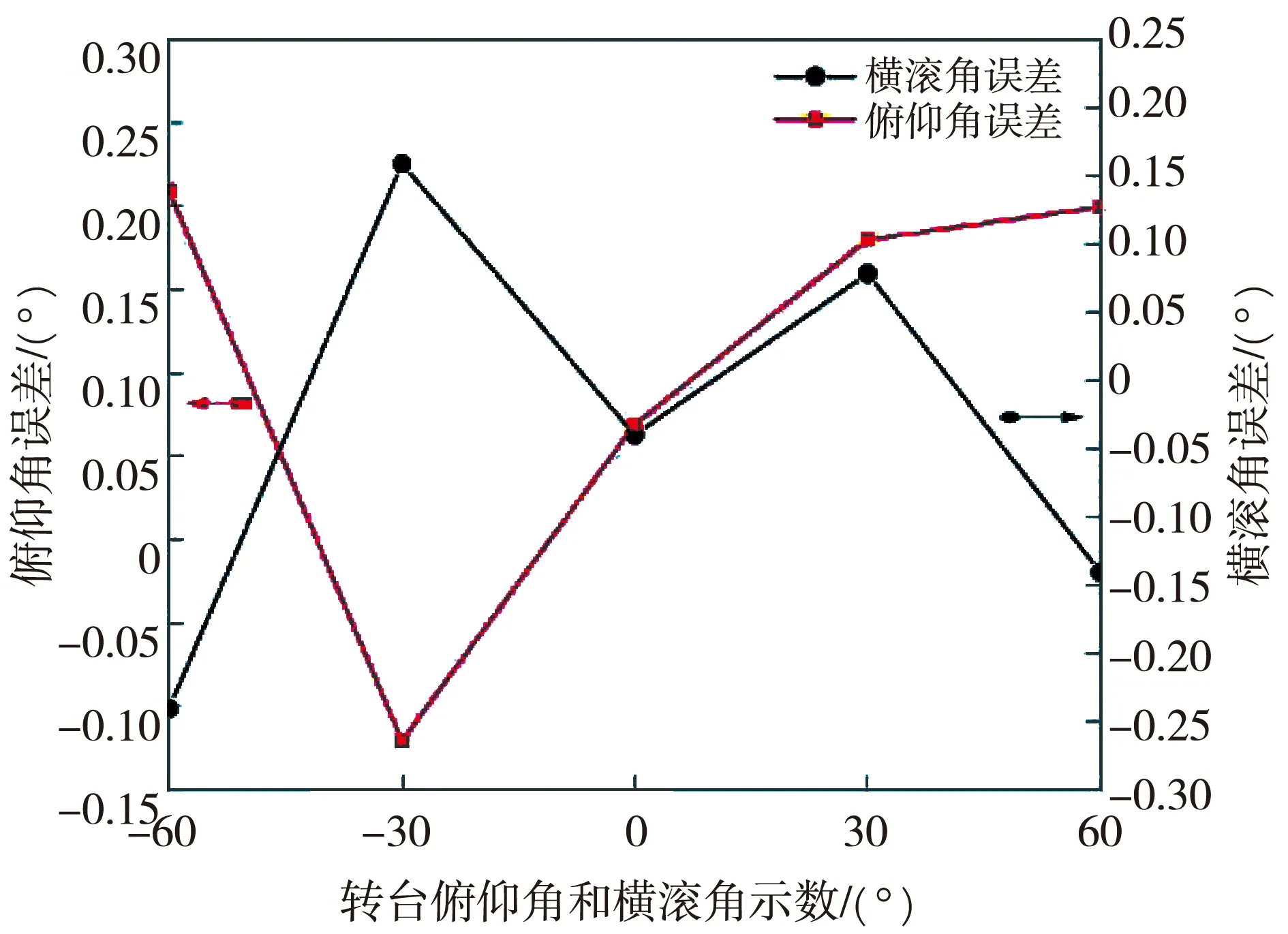
图2 静态恒定时的俯仰角和横滚角误差
从图2 可以看出, 不同倾角时, 俯仰角θ和横滚角φ的误差均不超过0.25°。
2)变化θ与φ, 将输出信号每隔30°左右记录一次, 得到误差如图3 所示。

图3 静态恒定时的航向角误差
从图3 可以看出, 当倾角增大时, 航向角ψ的误差也变大, 误差最大不超过0.5°。
3.2 动态变化实验
旋转转台某轴, 使θ,φ,ψ中的两个角保持恒定, 另外的一个角为动态变化。采集这两个恒定角的姿态信息输出, 与对应的转台示值进行比较, 得出不同动态条件下的航姿误差。分别改变θ,φ和ψ, 利用3组试验结果来评估系统动态性能。
1)保持ψ和φ不变, 改变θ, 使其保持动态变化。记录ψ,φ输出和转台示值, 结果如图4 和图5 所示。图中, 恒定未变的参考值为转台示值, 值随时间变化的曲线中, 幅度较大的为量测值, 未融合传感器数据, 幅度较小的为EKF结果。
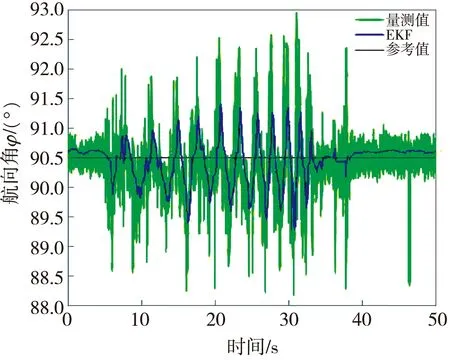
图4 俯仰角动态变化时的航向角滤波效果

图5 俯仰角动态变化时的横滚角滤波效果
由图4 和图5 可以看出, 量测值误差较大,ψ最大误差约为 2.5°,φ误差小于1.25°; EKF融合传感器数据后,ψ误差不超过 1.5°,φ误差不超过0.5°。
2)保持ψ和θ不变, 改变φ, 使其保持动态变化。记录ψ,θ的输出和转台示值, 结果如图6 和图7 所示。
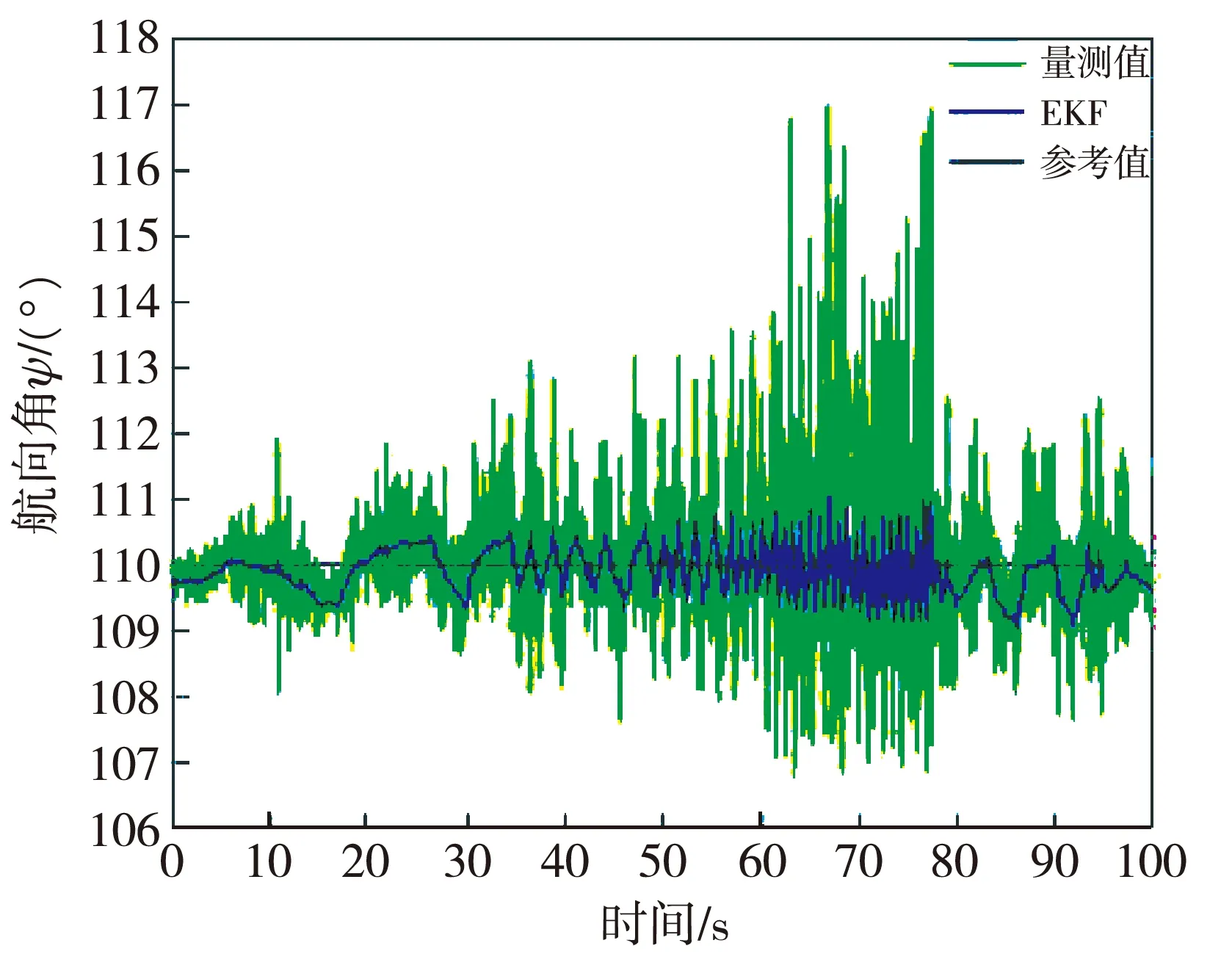
图6 横滚角动态变化时的航向角滤波效果
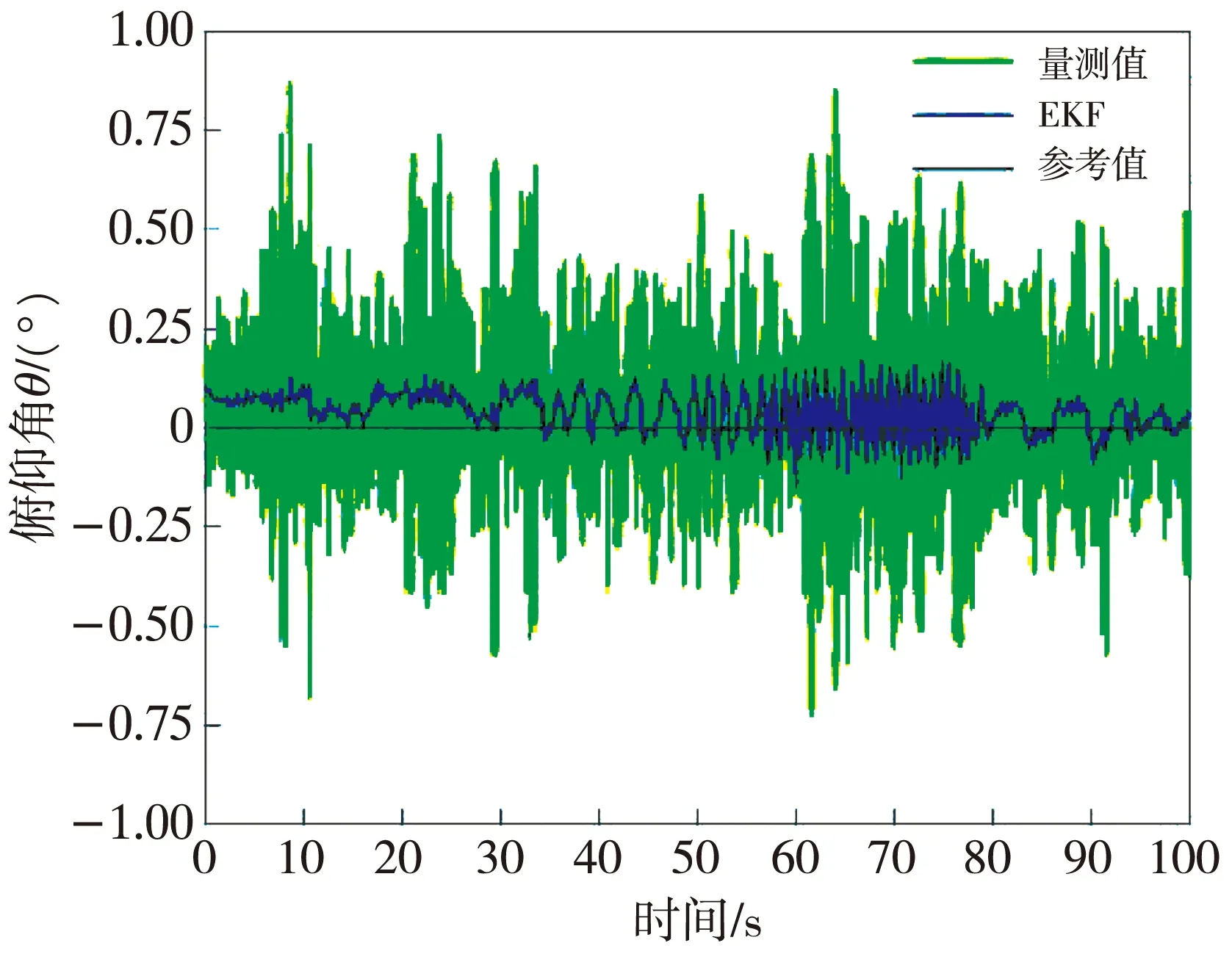
图7 横滚角动态变化时的俯仰角滤波效果
由图6 和图7 可知,φ处于动态变化时, 量测值误差较大,ψ最大误差约为 7°,θ误差小于1°; EKF融合后,ψ最大误差降低到约2°,θ误差不超过0.25°。
3)保持φ和θ不变, 改变ψ, 使其动态变化。记录系统的φ和θ的输出和转台示值, 结果如图8 和图9。
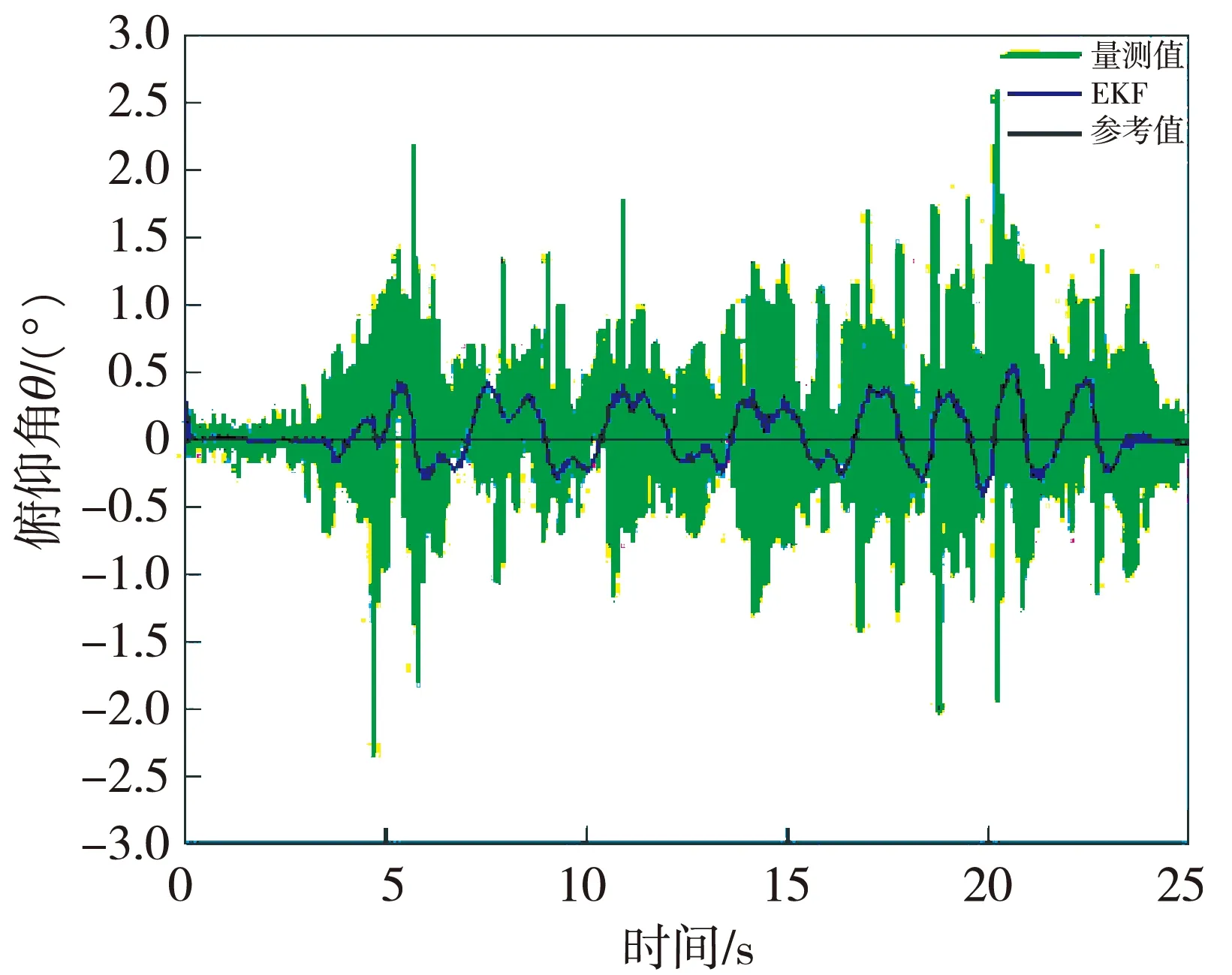
图8 航向角动态变化时的俯仰角滤波效果
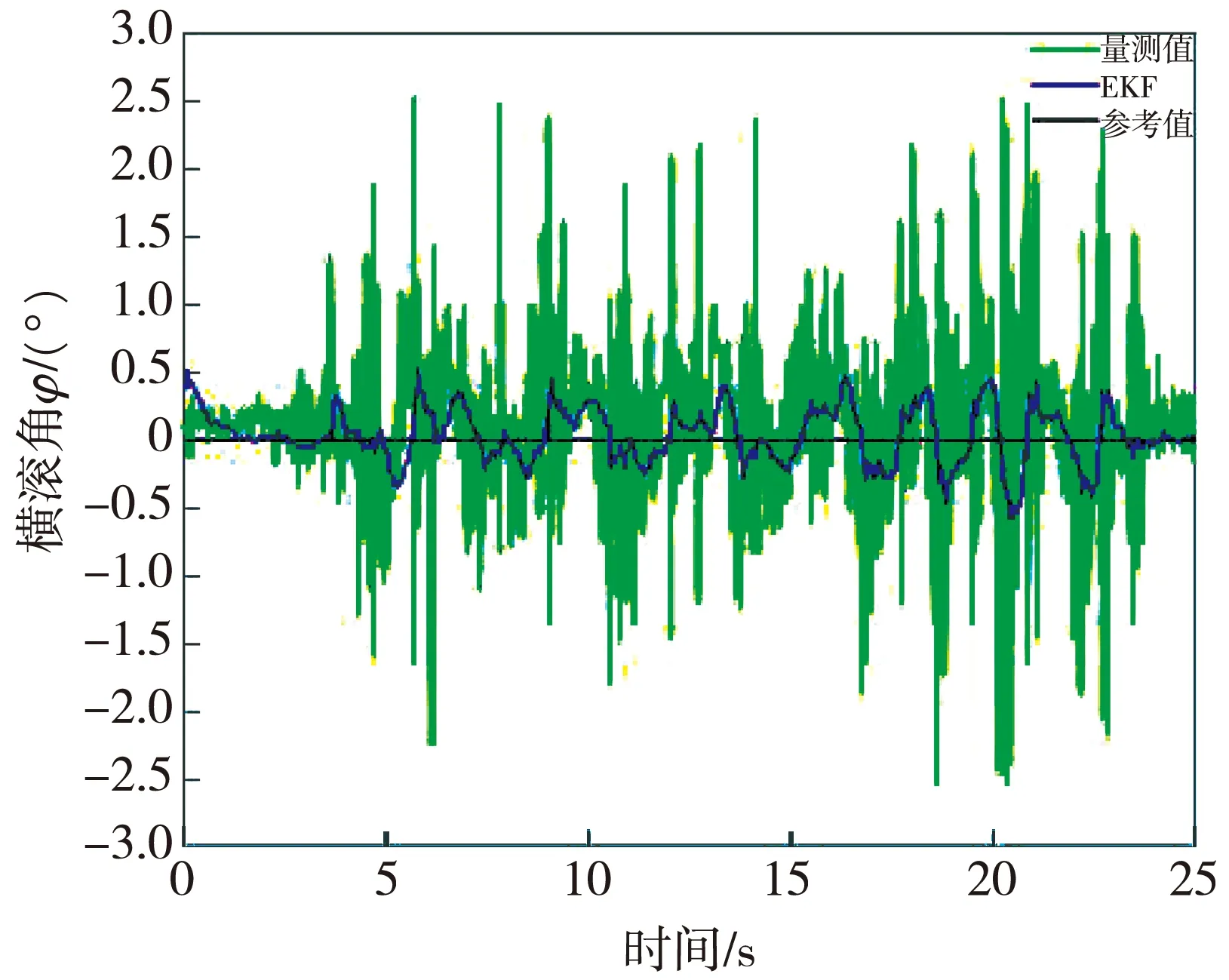
图9 航向角动态变化时的横滚角滤波效果
由图8 和图9 可以看出,ψ动态变化的情况下, 量测θ和φ的误差最大值均约为2.5°, EKF融合传感器数据后最大误差均降低为约0.5°。
系统的3种动态试验结果表明:
1)当θ动态变化时,ψ误差为±1.5°,φ误差为±0.5°。
2)当φ动态变化时,ψ误差为±2°,θ误差为±0.25°。
3)当ψ动态变化时,θ和φ误差均为±0.5°。结果表明, EKF 算法在不同动态变化情况时都能获得良好的滤波效果。
3.3 瞬变磁干扰实验
因为以上试验中没有周围环境的磁干扰, 所以EKF与AEKF的结果一致。为检验AEKF 算法在磁干扰环境下的性能, 进行如下试验: 将航姿系统置于转台, 因为仅航向角会受磁干扰的影响, 故只记录航向角读数。令转台保持静止, 手持一小块磁石反复移动, 持续数秒, 并对最终结果进行评估。图10 中, 恒定不变的为参考值, 曲线幅度变化最大的为量测值, 磁干扰时段航向角量测值出现的误差大至约80°; 幅度变化次之的为EKF算法情况下的滤波效果, 最大误差达到约70°, 对磁干扰的抑制效果有限; 变化幅度最小的为AEKF, 姿态和真实值之间的偏差在不同的时间段都很小, 被限制到约5°内。
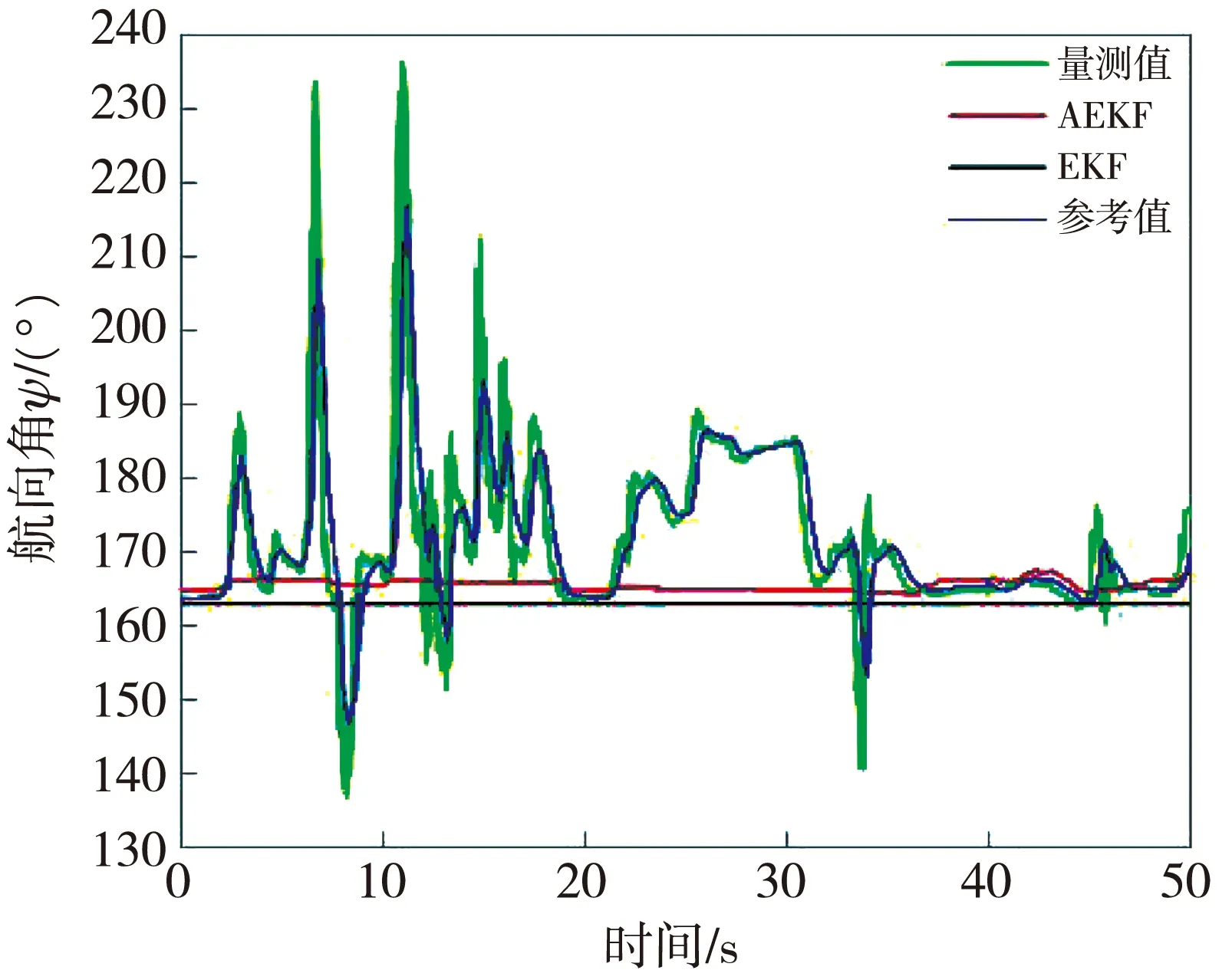
图10 瞬变磁干扰影响下的AEKF算法滤波效果
由此可见, AEKF 算法下的输出误差受限制性能良好, 且在磁干扰消失时也能很快收敛, 具有高可靠性和良好的抗磁干扰性能。
4 结 论
本文设计的微型无人机航姿系统, 利用EKF方法进行了数据融合, 通过静态、动态和磁干扰试验, 得出如下结论:
1)EKF 算法融合传感器数据后, 静态误差不超过0.5°, 动态误差不超过2°, 有效地提高了姿态角解算精度。
2)对EKF算法进行自适应改进, 对加速度量测噪声方差进行处理, 瞬变磁干扰最大误差从约70°下降到5°, 极大地提高了抗磁干扰能力。
3)系统能满足小型无人机的常规飞行控制需求, 适应应用环境, 具有较为广阔的发展空间。

