环枝状集输管网布局拓扑优化研究

张伟华

青海油田监督监理公司

随着国民经济的不断发展，油气资源的不断开发，集输系统在整个油气田地面工程建设中的投资占比越来越大，因此对井、站及管网的布局进行拓扑优化显得尤为重要[1-3]。集输管网的合理优化布局一方面可以减少初期产能投资，另一方面可以降低后期热力系统和动力系统的能耗。目前，对于管网布局优化已有大量学者进行了研究，通常以最短路径或最低投资成本为目标函数，采用多种优化算法进行迭代计算。熊友强等[4]通过调整最优粒子的编码顺序，采用粒子群算法对井口—计量站—联合站的三级布站模式进行了调整优化，优化后管道长度和投资费用有所降低；陈卓等[5]采用天鹰算法对星树状的气田集输管网进行布局优化，认为整体规划较分层规划方案更加合理；刘扬等[6]建立了适合于受约束条件下三维空间的管网布局模型，结合数字高程模型和广度优先搜索算法，对最优路径进行计算，取得了较好的效果。以上研究多针对放射状、环状或枝状的管网拓扑结构，形式相对较为单一，未见涉及环枝状复合型管网结构的相关报道。环枝状管网是将井口与阀组呈枝状连接，每个阀组所辖若干井，然后将阀组就近串联呈环状，并尽可能将中央处理厂或联合站置于环上。这种管网结构不仅在工程造价上较为经济，且在局部井口发生故障或施工作业时，其余油井不受影响，因此在部分油气田区块广泛应用。为此，建立适合环枝状集输管网优化的混合整数非线性规划模型，在离散决策变量空间下，获得固定约束条件下的环枝状集输管网优化方案，可为油气田地面工程设计与施工提供实际参考。

1 优化数学模型

1.1 建立目标函数

对环枝状集输管网进行布局优化，主要是考虑各阀组与中央处理厂的位置关系，以及井与阀组，阀组与阀组之间的管网连接关系，并对这些关系进行优化[7-8]。以总投资费用最小为目标函数，将管网投资分为3 部分：①从井到阀组的管道，其为一级管线；②阀组接到环上的管道及环间管道，其为二级管道；③阀组和中央处理厂的价格，对应公式如下：

式中：F为集输管网总投资费用，元；N、M分别为井和阀组数量；σij为第i口井到第j个阀组的连接关系，连接时σij=1，反之σij=0；Lij为第i口井到第j个阀组的管道长度，m；Aij为第i口井到第j个阀组的管道单位长度价格，元；K为与阀组对应的环上节点数量；θjq为第j个阀组到第q个节点的连接关系，连接时θjq=1，反之θjq=0；Hjq为第j个阀组到第q个节点的管道长度，m；Bjq为第j个阀组到第q个节点的管道单位长度价格，元；λ为环长度，m；C为环单位长度价格，元；fj为第j个阀组价格，元；e为中央处理厂价格，元。

1.2 设定约束条件

对于集输管网，要分别满足多项约束，其中井式约束表示每口井只能隶属一个阀组；集输半径约束表示要保证采出液从井口输送至阀组，其集输半径受温度、压力限制，进而影响最大集输半径；处理量约束表示每个阀组受限于产能开发和站内连头数量，必须保证产量分配均衡；节点流量平衡约束表示流入任何一个节点的流量满足守恒定律；双层布局约束保证环上节点数量与节点间管道数量相等，避免形成树状或星状结构[9]。计算公式如下：

式中：S为阀组管辖的井数量；R为集输半径，m；Qj为第j个阀组的处理量，m3/d；Qmax为第j个阀组的处理量上限，m3/d；qDi和qWi为流入、流出第i个节点流量，m3/d。

2 求解方法

以上建立的目标函数，存在3 个方面的求解难点：①各阀组的位置信息组合众多；②阀组位置确定后，各井口的接入方式和归属组合众多；③阀组接入环网的组合众多。此类问题属于混合整数非线性规划领域，已被证明属于NP 难题[10-11]。为了保证时间复杂度和空间复杂度的平衡，在此采用果蝇优化算法进行求解。

果蝇算法是基于果蝇觅食行为的全局优化算法[12]，将已知井的位置作为果蝇个体编码，以公式（1）为适应度函数，将阀组位置和各级管线长度作为决策空间变量，在公式（2）的约束条件下，对决策变量不断随机初始化，得到最小适应度函数，其对应的决策变量即为最优拓扑结构。

算法流程如下：①随机初始化果蝇的坐标位置为X_axis 和Y_axis；②利用果蝇的嗅觉优势寻找食物的随机位置；③通过预先估计果蝇个体与原点之间的距离，再利用味道浓度判定值对适应度函数进行计算，求出果蝇个体位置处的浓度信息；④在果蝇浓度信息中选出果蝇浓度最小的一个位置；⑤保留最佳浓度值，果蝇群体向食物位置移动；⑥进入迭代计算，重复上述（2）～（5）步骤，并判断味道浓度是否优于前一次，如是，算法结束，得到对应的决策变量。

3 实例分析与应用

3.1 不同约束条件对管网布局的影响

鉴于集输管网在设计时需要考虑诸多因素，而井式约束、集输半径、处理量约束是主要的约束条件，所以分别考察了单独约束和整体约束下的模型差异性。以某油田为例，分析不同约束条件对管网布局的影响。该油田区块面积为10×106m3，共有15 口油井，油井坐标位置和产量见表1。

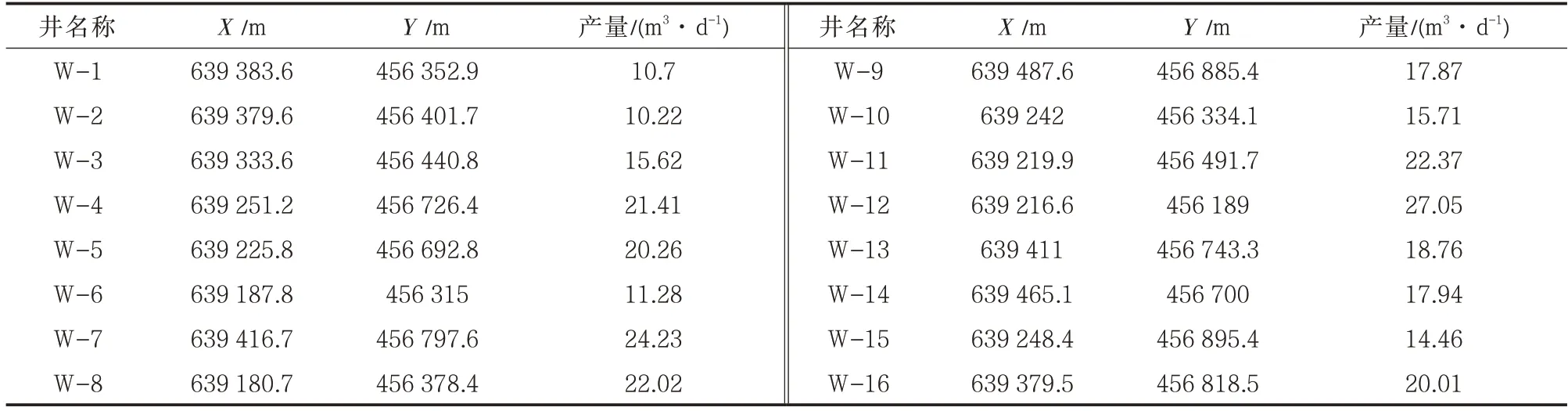
表1 油井坐标位置和产量Tab.1 Coordinate position and production of oil well

将油井至阀组的管道定为一级管线，其管径均为76 mm，单位长度价格为105.4 元/m；将其余管道定为二级管道，其管径均为114 mm，单位长度管道价格为168.1元/m。单个阀组的价格为70.21×104元，中央处理厂为561.64×104元。在种群规模20，最大迭代次数200 次的条件下，采用果蝇算法进行优化求解，结果见表2、图1。

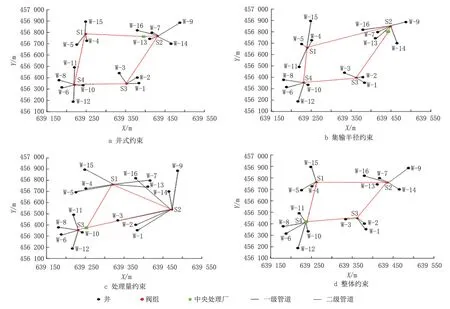
图1 不同约束条件下的管网布局Fig.1 Pipe network layout under different constraints

表2 不同约束条件下的管网投资构成Tab.2 Composition of pipe network investment under different constraints

当只考虑井式约束，每个阀组位于井组的边缘或中心，可有效减少一级管道长度，但W-9 井到S2 的距离为1 532 m，超过最大集输半径的限值，因此不能只考虑井式约束。

当只考虑集输半径约束时，各井的井口压能得到有效利用，一级管道长度有所减少，二级管道的长度有所增加。鉴于二级管道的单价较一级管道的单价高，在阀组数量不变的情况下，投资费用有所增加，且各个阀组分配的流量不均匀，一旦后期出现新井或部分井存在故障时，对环状管网的流量冲击较大。此外，W-12 井已接近最大集输半径，当油井采出液有所降低时，无法保证输送至对应阀组。

当只考虑处理量约束时，所需的阀组数量最少，一级管道的长度有所增加，二级管道的长度有所减少，距离S1 较近W-16 井未进入S1，而是进入到S2，且W-3 井的集输路径几乎与主环路径相同，多数井组的集输半径超过限值，不利于井口压能的有效利用。

综合考虑三种约束时，阀组均位于井组边缘，连接井口的数量较均匀，且环的长度较短，中央处理厂与阀组S4 合并设置，可有效减少建设征地。与单独考虑井式约束相比，一级管道长度基本不变，但二级管道长度大幅降低，因此投资费用较低。此外，不同约束条件下，阀组和中央处理厂的位置和管网结构有所差异，优化的管网结构均为上层枝状、下层环状，说明了本文模型的具有准确性和可靠性。以整体约束得到的投资费用为基准，集输半径约束对投资费用的影响远大于井式约束和处理量约束。

3.2 不同优化条件对管网布局影响

以往研究人员从井、阀组、环、中央处理厂分别逐级建立各自模型[13-14]，并进行分层优化，得到局部最优解。为验证本算法的准确性，将分层优化与整体优化结果进行对比（表3）。与整体优化相比，分层优化是先优化井到阀组的距离，后优化环之间的距离，故其一级管道长度有所降低，但二级管道长度有所增加，导致总费用增加。整体优化将整个管网系统视为一个整体，变量之间经历了多次最优解集的筛选，形成的阀组位置和数量能够较好地平衡环状和枝状结构的费用组成，优于分层优化设计。

表3 分层优化和整体优化下的管网投资构成Tab.3 Composition of pipe network investment under hierarchical optimization and overall optimization

3.3 不同优化算法对比

为验证果蝇算法的优越性，将其与Prim、粒子群、模拟退火算法优化结果进行对比，其中Prim算法为局部优化算法，粒子群和模拟退火算法为全局优化算法（表4）。四种算法的最大迭代次数均为200，种群规模为20，Prim 算法通过不断进行最小数生成，无固定参数设置；粒子群算法中设置惯性权重从0.9 线性递减至0.4，加速因子取为2.0；模拟退火算法中设置初始温度100 ℃，降温系数0.99，终止温度0.01 ℃；本算法中设置初始权值0.8，权值系数1.1。

表4 不同优化算法对比Tab.4 Comparison of different optimization algorithms

结果显示Prim 算法的优化效果最差，一级管道和二级管道长度较只考虑井式约束时还长，且收敛迭代次数和计算时间较长，当井和阀组数量较多时，时间复杂性和空间复杂性将呈爆炸式增长，不利于提高计算效率。粒子群和模拟退火算法与本算法的优化效果相近，但均在最大迭代次数附近收敛，说明这两种算法不易跳出局部最优解的限值，对于集输管网优化这类多约束的多维多峰函数的寻优不具备优越性。综上所述，本算法在求解稳定性和收敛速度上具有一定的科学性和可靠性。

4 结论

（1）以总投资费用最小为目标函数，基于多种约束条件，建立了环枝状集输管网布局拓扑优化模型，考察了不同约束条件对优化结果的影响，结果表明，集输半径约束对投资费用的影响远大于井式约束和处理量约束。

（2）整体优化将整个管网系统视为一个整体，形成的阀组位置和数量能够较好地平衡环状和枝状结构的费用组成，整体优化较分层优化结果更加合理。

（3）针对本文算例，果蝇算法的收敛迭代次数为35，计算时间12.13 s，与其余求解算法进行对比，在求解稳定性和收敛速度上具有一定的科学性和可靠性。