基于特征提取的电气设备红外图像识别算法

党晓婧, 刘顺桂, 朱光南, 栾孟杰, 沈民强

(1. 中国南方电网有限公司 深圳供电局电力科学研究院, 广东 深圳 518000; 2. 浙江大立科技股份有限公司 a. 技术服务部, b. 生产部, 杭州 310000; 3. 绥化学院 信息工程学院, 黑龙江 缓化 152061)

输变电设备是构成电力系统的基础设备,输变电设备的安全、稳定运行直接影响电力系统的可靠性,因而全面掌握输变电设备的运行状态是保障电力供应的必要条件[1-2].此外,新兴技术在电气设备检修运维方面的应用具有重要的理论意义和实际价值.

智能巡检机器人、无人机等先进装备在电气设备巡检过程中的应用,显著提高了工作效率,降低了巡检人员的工作强度,缓解了电网规模日益扩张与人员配置不足之间的矛盾[3-4].但从大量图像数据中获取有用信息,实现电气设备的准确识别与故障判断,成为了当前电力巡检工作急需解决的问题[5-6].

计算机视觉技术的发展使得电气设备的图像识别与故障诊断技术有了新的突破[7-8].周可慧等[9]针对电气设备红外图像分辨率差、识别度低等问题,采用RGB、HSV颜色空间转化和SeamCarving缩放处理建立了CNN-Alex网络,使得设备识别准确率提高到97.7%.朱正国等[10]针对配电网无人化管理的要求,提出了一种BRISK算法与平移因子相结合的图像识别方法,实现了对配电设备危险情况的准确识别.张从新等[11]利用多种形态学处理算法,并结合Canny算子实现了复杂背景下的输电线路设备识别.王启银等[12]基于形态学权重自适应算法研究了变电站电气设备的图像分割处理方法,显著提高了变电站设备红外图像的特征提取准确率与识别准确度.江泽涛等[13]提出了一种改进脉冲耦合神经网络的红外与可见光图像融合算法,并采用静态小波变换融合策略,显著提升了融合图像的清晰度及信息熵.

利用人工智能算法实现对电气设备及其故障的识别与分类始终是国内外研究的重点[14-16].本文针对智能变电站巡检机器人对变电站设备红外图像识别问题,研究了基于矩函数的特征提取技术在电气设备红外图像识别中的应用.本文从矩函数的一般定义出发,以数字图像的几何矩为基础,导出包含图像特征信息的不变矩,提取图像特征参数,并利用神经网络分类算法完成了电气设备的红外图像分类识别.

1 基本概念

统计学上,矩表征了随机变量的分布情况.例如,随机变量的期望可以定义为一阶原点矩,即

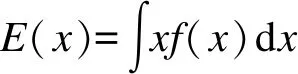
(1)

式中,f(x)为随机变量的概率密度.随机变量的方差可以定义为二阶中心矩,即

(2)

对于一幅图像函数而言,假设像素点(x,y)处的亮度值由像素p(x,y)表示,则其i+j阶矩函数表达式为

(3)

式中:ξ为函数的定义域,即平面图像所在的区域;Ψij(x,y)为定义域内关于(x,y)的连续函数,又称矩的权核.

数字图像中计算得到的矩集描述了图像形状的全局特征,同时包含各种不同类型的几何特性.因此,可将图像矩的这种特性描述能力应用于图像分类与识别.

1.1 几何矩

几何矩属于矩函数的一种,其核函数为像素坐标的幂.对于一幅图像而言,像素点坐标的变换可用矩空间相应的变换进行表达与分析.此外,相比核函数为复数的情况,在计算机处理过程中几何矩更易被执行与完成.

定义一幅数字图像的i+j阶二维几何矩为mij,即

(4)

图像的不同阶几何矩表征了图像不同亮度分布的空间特性,因此,利用几何矩集来构建图像的特征集具有良好的理论依据.零阶几何矩表征了一幅图像的总亮度,若图像由二值函数表示,则零阶几何矩表征目标区域的亮度为

(5)

一阶几何矩有两个,分别为m10与m01,且分别对应图像关于x轴和y轴的亮度矩.对于二值图像而言,矩心(x0,y0)给出了图像目标区域的几何中心,其计算公式为

(6)

通常将参照系的原点移至图像亮度矩心的几何矩称为中心矩,其计算表达式为

(7)

图像的这一变化,使得矩的计算可以独立于图像的参照系.由此,可以利用中心矩导出不受图像平移、旋转、缩放影响的特征量,将其应用于图像识别.

1.2 图像矩函数的不变量

根据矩函数的定义可知,中心矩本身具有平移不变性.这是由于中心矩是利用图像的中心为坐标原点进行定义的,而图像中心不受坐标移动的影响.因此,由几何矩直接计算得到的二阶、三阶中心矩也保持平移不变的特性.

对于缩放不变量,假设图像的像素坐标经过相同的尺度缩放因子k变换,则

(8)

dx′dy′=k2dxdy

(9)

尺度变换后图像几何矩可由原始图像的几何矩进行表示,即

m′ij=ki+j+2mij

(10)

且有

m′00=k2m00

(11)

消去式中的未知尺度因子k得到

(12)

因而可得在图像的平移与缩放变换下保持不变的φij函数,即

(13)

假设图像的旋转角度为θ,则

(14)

变换后的图像几何矩为

p(x,y)dx′dy′

(15)

计算可得

(16)

(17)

由式(16)和(17)可知,m20+m02具有旋转不变性,即

m′20+m′02=m20+m02

(18)

若用φij代替mij,即可得到几何矩不变量函数.这些函数均具有旋转不变性、平移不变性和缩放不变性,因此,可以用于描述图像的本质特征且不受图像平移、缩放、旋转的影响.图像识别中常用几何矩不变量表达式为

I1=φ20+φ02

(19)

(20)

I3=(φ30-3φ12)2+(φ03-3φ21)2

(21)

I4=(φ30+φ12)2+(φ03+φ21)2

(22)

(23)

(24)

计算过程中发现矩不变量I1～I6数值较小,且变化范围较大,应用过程中不便计算.为了简化计算、便于比较,对上述不变矩进行修正,同时消除可能出现的负值,其表达式为

Zi=|lg|Ii|| (i=1,2,…,6)

(25)

Lena图为图像处理中使用最广泛的标准测试图之一,本文利用该图来测试修正前后不变矩参数的变化特征.图1为本文测试中采用的Lena图,处理过程中将其转换为一个450×450的灰度信息矩阵,然后计算其不变矩参数.表1为修正前后Lena图不变矩的计算值.

表1 Lena图像不变矩修正前后比较

图1 Lena图

由表1可知,修正前不变矩的数值较小,数量级差异较大且还可能出现负数.修正后的不变矩值比修正前的值大,数量级差异较小且不包含负数,因此,具有更强的可比性,便于图像识别和匹配处理.

2 不变矩的改进

经过平移、旋转、缩放变换的图像在处理过程中会产生重复采样和重量化的误差,导致不变矩的准确性降低.为了消减这种对图像识别的影响,定义改进后的中心矩表达式为

p(x,y)dxdy

(26)

式中,x″和y″为修正系数且分别定义为

(27)

修正后用于表征图像特征的不变矩仍由式(19)～(24)计算得到.

目标图像p(x,y)经(Δx,Δy)平移后的图像p′(x,y)可表示为

p′(x,y)=p(x-Δx,y-Δy)

(28)

将式(28)代入式(26)可得

p(x-Δx,y-Δy)d(x-Δx)d(y-Δy)

(29)

令zx=x-Δx,zy=y-Δy,式(29)可整理为

p(zx,zy)dzxdzy

(30)

分析可知,式(30)与式(26)是等价的,即原图像p(x,y)和平移后的图像p′(x,y)的中心矩相同.

对原图像p(x,y)进行比例系数为k的缩放变换,则

(31)

将缩放后的图像代入式(26),计算得到中心矩,即

kp(x,y)dxdy=ki+j+2μij

(32)

由式(32)可知,缩放前后的归一化中心矩也是等价的.因此,可以证明改进后的中心矩具有缩放不变性.

3 算法验证

为了验证I1～I6不变矩的特征提取效果,选择变电站设备红外图像经分割后得到的二值图像不变矩参数进行计算.图2为变电站原始红外图片,图3为对红外图像进行分割提取处理后的二值图像.

图2 变电站设备红外图像

图3 典型变电站设备二值图像

采用改进前后的不变矩计算方法,计算图3b～d不变矩与图3a不变矩的差异值,结果如图4所示.由图4可知,对于同一设备而言,改进后的不变矩数值优于改进前.通过对计算方法的改进能够降低由于图像平移、旋转、缩放造成的计算误差.

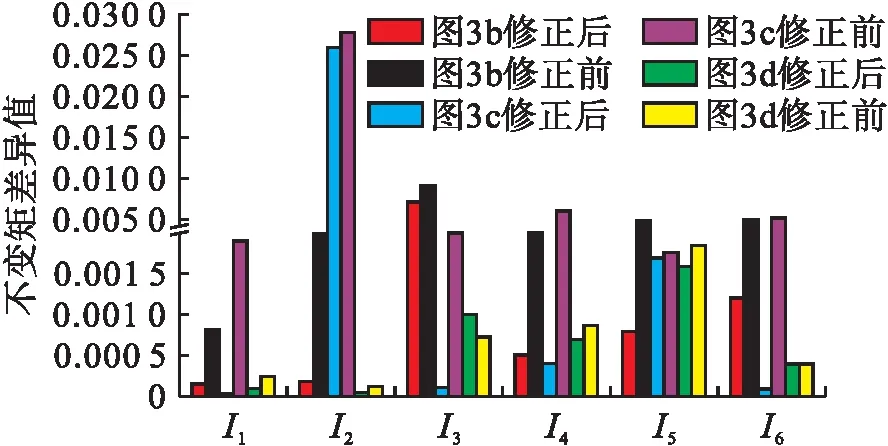
图4 不变矩改进前后差异值比较

对图3进行不变矩计算,计算结果如表2所示.对比计算3b～d不变矩与图3a不变矩的差异值,结果表3所示.由表3可知,不同设备不变矩差异值要明显大于同一设备的不变矩差异值,不同设备的均值与方差变化较大而同一设备较小,说明不变矩参数能够较好地反映不同设备之间的差异,有利于设备识别.同一设备的旋转变化会造成不变矩差异的扩大,缩放变化对不变矩造成的影响较小,因此,在获取图像过程中要尽量减少镜头的转动,保持图像的稳定性.

表2 典型设备图像不变矩阵计算结果

表3 典型设备图像不变矩差异值比较

选取绝缘子、电流互感器、避雷器、隔离开关4种分割后的变电站典型设备图像30幅,并对图像进行顺时针旋转60°、垂直方向镜像、缩放0.5倍和2倍处理,得到共计600幅图像并将其作为输入样本并进行神经网络训练.选择4种典型设备的红外图像各50幅进行神经网络分类识别,识别结果如表4所示.由表4可知,利用各类设备红外图像的不变矩作为特征提取参数,对其进行识别综合识别率可达94%,能够满足实际应用需求.

表4 神经网络分类识别结果

4 结 论

本文研究了电气设备红外图像的特征提取方法,从矩函数的数学概念出发,建立表示图像特征的几何矩,推导矩函数的平移、缩放、旋转不变性,得到6个用于图像识别的几何矩不变量,得到如下主要结论:

1) 在不变矩的基础上,设计改进的中心矩计算法可以消除由于图像变换过程中造成的计算误差,能够有效提高不变矩参数计算的准确性;

2) 采用本文提出的6个不变矩作为电气设备的红外图像特征参数,利用神经网络对图像进行训练与识别,其识别准确率可达94%,能够满足实际应用需求.