基于经验模态分解-粒子群优化-长短期记忆的车间电力能耗预测方法

孙宁可,王 艳,纪志成

(江南大学 物联网技术应用教育部工程研究中心,江苏 无锡 214122)

随着“智能制造”、“边缘计算”和“大数据”等创新理念的提出,如何运用采集的实时数据和智能化算法来改善生产过程是当前的一种发展趋势[1]。电力能耗数据相较于其他具有设备特有性的运行数据来说有更好的普适性,而且随着工业的进一步发展,节能减耗也是一个重要的着力点[2]。在工业生产过程中,电力能耗数据具有很重要的意义,对生产设备能耗进行预测和对比分析有助于检测设备工作异常状态、提前预知生产风险。车间的能耗预测是新型能源管理系统的重要模块,实时、精准的能耗预测能够帮助分析未来能源消耗趋势,进而合理分配能源,减少不必要的能源浪费,有助于降低车间生产的能源成本[3]。

电力能耗预测属于时间序列预测问题,其主要预测方法包括传统预测方法和神经网络方法[4]。传统预测方法有指数平滑法、时间序列法和回归预测法等,受到方法限制,预测精度已经不能满足要求[5]。神经网络方法有人工神经网络、支持向量机、反向传播(Back propagation,BP)神经网络、长短期记忆(Longshort-term memory,LSTM)网络等,预测精度更高[6]。

文献[7]提出了将支持向量回归和基于局部加权回归的周期趋势分解结合起来的短期电力能耗预测方法,将数据分解后,再利用支持向量回归方法进行预测,相较于随机森林回归和只采用支持向量回归方法,预测精度更高,但是支持向量回归方法中的惩罚因子参数和核函数参数仍按经验选取,无法充分发挥该方法的预测能力。文献[8]提出了一种组合预测方法,结合了经验模态分解(Empirical mode decomposition,EMD)算法和LSTM网络,利用EMD进行序列分解,然后利用LSTM网络进行预测,与单一的LSTM网络相比,预测精度较高,但是LSTM网络中的训练迭代次数和神经元个数等参数也需按经验选取,未能考虑到对LSTM网络的内部参数进行寻优。文献[9]提出了一种组合电力能耗预测方法,结合了LSTM网络和卷积神经网络,使用卷积神经网络进行特征提取,然后经卷积层和池化层处理后作为LSTM网络的输入,得到了较高的预测准确率,但是并没有考虑到对电力能耗数据进行分解后再进行预测,也没有考虑到对神经网络的内部参数进行寻优。文献[10]将BP神经网络与EMD分解相结合,提出了一种磁悬浮冷水机组的能耗预测方法,经过分解、预测和重构后,能够较为准确地预测冷水机组能耗,虽然通过设置不同的隐含层层数和神经元数目来对比分析预测效果,但是对比不够充分,不能确定是否得到最优参数。

综上所述,为了能够提高电力能耗预测的准确性并充分发挥LSTM网络的预测性能,本文采用EMD算法将电力能耗序列分解为多个本征模函数(Intrinsic mode function,IMF)分量和趋势分量,然后采用LSTM网络来对每个分量进行独立预测,将每个分量的预测结果进行叠加得到最后的电力能耗预测结果,同时,考虑到LSTM网络的内部参数通常是按照经验设置,不能实现最佳的预测效果,因此利用粒子群算法来确定LSTM网络中神经元个数和训练迭代次数的参数设置,最优化LSTM网络的预测性能。最后,将所提算法应用于江苏某药企中药制造车间的实测车间电力能耗数据集来进行验证。

1 方法及原理

1.1 经验模态分解

EMD算法是一种信号处理方法,主要应用于时间序列[11]。与小波分析不同[12],对于一段未知信号,EMD无须预先设定任何基函数,具有很好的普适性。EMD分解算法可将样本分为有限个数据分量,每个分量代表原数据样本的一部分特征,将每个分量叠加后,理论上就会还原原始数据样本的全部特征[13]。其分解流程如图1所示,具体步骤如下。

图1 EMD分解计算流程

(1)采用三次样条法将原始信号x(t)的极大、极小值连成包络线;

(2)求其均值,得到均值包络线m1(t);

(3)求原始信号x(t)与均值包络线m1(t)的差,得到h1(t)

h1(t)=x(t)-m1(t)

(1)

(4)如果h1(t)不符合IMF条件。令h1(t)为x(t),回到第一步,进行第二次选取,如式(2)所示

h2(t)=h1(t)-m2(t)

(2)

式中：m2(t)为h1(t)的均值包络线。重复进行k次,得到hk(t)

hk(t)=hk-1(t)-mk(t)

(3)

若hk(t)符合IMF条件,则hk(t)就是第一个IMF分量c1(t)

c1(t)=hk(t)

(4)

(5)x(t)与第一个IMF分量c1(t)做差,得到余项r1(t)

r1(t)=x(t)-c1(t)

(5)

(6)循环执行n次得到余量r2(t),r3(t),…,rn(t),然后判断余量rn(t)的单调性,如果是单调函数,或者是常函数,满足二者之一就说明分解完成。得到若干个IMF分量ck(t)和一个趋势项rn(t)

(6)

车间电力能耗数据采用EMD算法进行分解后,能够得到若干个不同的分量,频率从高到低,其中各自包含了原始数据的部分特征,相较于原始数据具有更强的规律性。然后再利用LSTM网络进行处理和预测就能够得到每个数据分量的预测结果,各个分量的预测结果叠加后便可以得到对原始能耗数据的预测结果,这种分解、预测再重组的方式有助于充分提取数据特征、提高预测准确度。

1.2 长短期记忆网络

图2 LSTM网络隐含层内部记忆单元结构

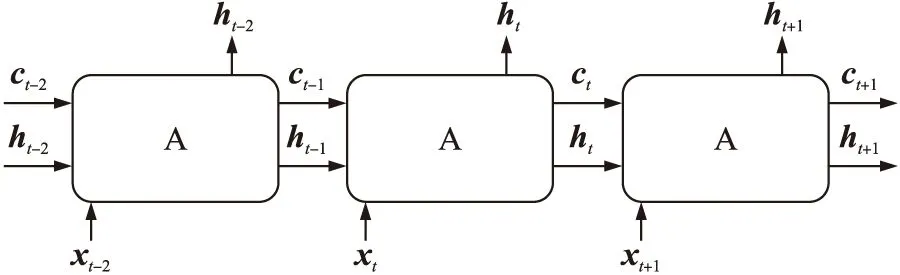
图3 LSTM网络信息传递过程

具体实现过程如下：

计算遗忘门的输出值ft

ft=σ(Whfht-1+Wxfxt+bf)

(7)

式中：Whf、Wxf为遗忘门的权重矩阵;bf为遗忘门的偏置向量[16]。

计算输入门的值it

it=σ(Whiht-1+Wxixt+bi)

(8)

式中：Whi、Wxi为输入门的权重矩阵;bi为输入门的偏置向量。

计算记忆单元的输入状态

(9)

式中：Whc、Wxc为细胞状态的权重矩阵;bc为细胞状态的偏置向量。

更新细胞状态

(10)

计算输出门的值ot

ot=σ(Whoht-1+Wxoxt+bo)

(11)

式中：Who、Wxo为输入门的权重矩阵;bo为输入门的偏置向量。

计算t时刻的隐藏层输出

ht=ot∘tanh(ct)

(12)

三个门结构的相互配合使得LSTM网络具有了一定时期内的记忆能力,并且可以遗忘和删除部分信息,能够更好地处理时间序列数据,因此采用LSTM网络来对电力能耗数据进行预测相较RNN具有更高的准确度和稳定性。

1.3 粒子群优化算法

粒子群优化(Particle swarm optimization,PSO)算法基于进化计算技术[17],其基本思想是：通过种群内各粒子之间的协同工作和信息共享来寻找最优解。在实际编程应用中,PSO借助一群只有速度和位置两个属性的个体来帮助计算,种群中粒子的速度和位置更新公式如式(13)所示

(13)

粒子最优位置更新如式(14)所示

(14)

种群最优位置更新如式(15)所示

(15)

本文主要使用PSO来对长短期记忆网络的参数进行寻优,主要参数有两个：神经元个数和训练迭代次数。具体寻优流程如图4所示,其中适应度函数选取为LSTM网络训练后的均方根误差,通过粒子群算法的不断迭代寻优,找到能够使LSTM网络训练后的损失函数最小的上述两个参数值。

图4 PSO寻优流程图

2 EMD-PSO-LSTM预测模型

2.1 预测模型作用流程

EMD-PSO-LSTM预测模型的作用流程如图5所示,具体步骤如下：

图5 EMD-PSO-LSTM模型预测流程图

(1)对原始车间电力能耗数据进行EMD分解,得到具有各自特征的IMF分量和趋势分量;

(2)对分解得到的各个IMF分量和趋势分量进行数据归一化,并划分为训练集与预测集;

(3)分别以各个IMF分量和趋势分量的训练集数据为输入进行各个LSTM网络训练,同时采用粒子群算法对各个LSTM网络的神经元个数和训练迭代次数进行寻优,找到各个LSTM网络的最优参数组合;

(4)应用按照最优参数设置并训练完成的LSTM网络分别对各个分量进行预测,得到各个分量预测结果;

(5)预测结束后,对各个分量的预测结果进行反归一化,并将预测结果进行叠加,最终获得对原始车间电力能耗数据的预测结果。

2.2 电力能耗数据EMD分解结果

电力能耗EMD结果如图6所示,图6(a)、图6(b)和图6(c)是分解出的IMF分量,图6(d)是电力能耗序列的趋势分量,其中都包含了电力能耗数据的部分特征。EMD分解将原始电力能耗序列的特征分别提取了出来,分解得到的信号具有更明显的周期变化性,更适合采用LSTM网络进行预测。

图6 EMD分解结果

2.3 粒子群算法寻优效果

以分量IMF2为例,分别采用按照经验选取参数的LSTM网络和PSO算法参数寻优的LSTM网络进行预测,预测结果如图7所示。PSO算法迭代过程如图8所示,可以看出当迭代次数大于33时,LSTM网络训练后的均方根误差即适应度函数趋于稳定,此时,神经元个数取256,训练迭代次数取198。

图7 IMF2预测效果对比图

图8 粒子群优化迭代过程

从图7可以看出,PSO-LSTM方法预测准确度要高于单一的LSTM预测,为求对预测结果进行定量分析,选取均方根误差(RMSE)和平均绝对百分比误差(MAPE)作为量化依据,结果如表1所示。

表1 IMF2预测结果对比表

(16)

(17)

式中：yi为实际能耗数据,xi为预测值。

根据表1所示,PSO-LSTM相较于单一的LSTM网络而言,预测结果的两个误差都更小,因此,预测准确度更高,预测稳定性也较好。

3 试验结果与分析

在本试验中,采用江苏某药企中药制造车间的电力能耗数据验证本文算法。所用的车间电力能耗数据如图9所示,选择2021年7月2日至2021年7月6日的数据作为训练数据,2021年7月7日的数据作为测试数据,数据时间间隔均为1 h。

图9 车间电力能耗数据

分别使用RNN模型、LSTM模型、PSO-LSTM模型、EMD-LSTM模型和EMD-PSO-LSTM模型进行预测,预测结果如表2所示。

表2 各模型预测结果对比表

各模型预测结果如图10所示,图10(a)～(e)分别是RNN模型、LSTM模型、PSO-LSTM模型、EMD-LSTM模型和EMD-PSO-LSTM模型的预测结果与实际电力能耗测试数据的对比图。图10(f)则是所有模型预测结果的对比图。各模型预测准确度从高到低依次是：EMD-PSO-LSTM模型、EMD-LSTM模型、PSO-LSTM模型、LSTM模型和RNN模型。

图10 各模型预测结果及对比

结合表2与图10的各项数据可以清晰看出：相较于RNN模型,LSTM模型对电力能耗数据的预测准确度更高,说明LSTM网络能够更好地处理电力能耗数据;而相较于单一的LSTM模型,EMD-LSTM模型和PSO-LSTM模型的预测准确度又有明显的提升,分别体现了数据分解和网络内部参数寻优在提高预测精度方面的作用;EMD-PSO-LSTM模型通过使用PSO算法对各分量的LSTM模型进行参数寻优,预测准确度相较EMD-LSTM模型和PSO-LSTM模型又有明显的提升。

4 结束语

本文通过引入EMD算法和PSO算法,把时间序列的电力能耗数据分解为各个IMF分量和趋势分量,并将更好地反映了原始能耗数据不同特征和变化趋势的各分量输入LSTM网络进行预测,然后整合预测结果。同时对分别用于预测各分量的各个LSTM网络进行粒子群算法参数寻优,相较于按照经验选取LSTM网络参数的EMD-LSTM模型,准确度有明显提高。试验结果表明,本文提出的EMD-PSO-LSTM电力能耗预测模型能够准确预测未来24 h内的电力能耗,预测精度较高,能够提供较为准确的电力能耗预测数据。