基于隐式数据的改进LFM-SGD 协同过滤推荐算法

李志豪，李仁港，蒋小菲

（贵州大学 大数据与信息工程学院，贵阳 550025）

0 引言

随着科技时代爆炸式的发展速度，“人工智能+大数据”引爆了时代热点，处于大数据时代中心的人们，将面临眼花缭乱的筛选。一方面既要花费大量时间进行数据的筛选，又很难从大量的数据中找出自己感兴趣的部分；另一方面也会使大量冗余信息成为网络中的“隐信息”［1-2］，无法被普通用户索取。个性化推荐模型能够根据用户的历史行为以及对物品的行为信息，向目标用户提供符合其兴趣的物品和信息。个性化推荐中使用的主流技术包括关联规则、深度学习、神经网络、知识图谱、聚类算法、协同过滤算法［3］等等。其中，协同过滤算法是目前推荐算法领域内应用最多的一类。

推荐算法的研究始于上世纪90 年代初期，经过30 多年的积累和沉淀，虽然已形成了较为成熟稳定的体系，但并没有形成统一的分类标准。2019 年，Serhii Chalyi 等人［4］提出了一种利用时间约束，在推荐系统冷启动情况下建立推荐的方法。该方法在时间约束的帮助下，虽然对兴趣周期性变化的“冷”用户，可以提高相应推荐的准确性，但相对来讲不够灵活，不能采用更多的信息进行预测计算。2021 年，Nam Le Nguyen Hoai 等人［5］提出了一种基于用户记忆的协同过滤推荐算法。该算法通过对目标函数的优化，虽然在一定程度上解决了冷启动的问题，但无法对数据稀疏性有更好的帮助。2022 年，吴锦昆等人［6］提出了一种基于改进相似度的协同过滤算法。该算法由改进皮尔逊相似度公式计算用户相似度，针对不同用户具有不同评价体系存在一定偏差问题，从引入用户差异因子来提高推荐的精度，取得了一定的效果，但该算法在用户评价数据规模较大的情况下，效果并不明显。

针对用户的评价数据规模大、数据稀疏、传统的矩阵分解算法响应缓慢、推荐精度和准确度低，以及冷启动等问题，本文在传统协同过滤和模型训练等推荐算法的基础上，结合矩阵分解［7］的思想，对隐式数据［8-9］进行调整，提出改进后的LFM-SGD 协同过滤推荐算法。采用改进后的矩阵分解思想，用随机梯度下降的思想来获得最优路径，通过隐式数据维度降低原始评分数据索引，对目标用户推荐其感兴趣且未接触过的物品，可以有效提高推荐算法的准确度。

1 协同过滤推荐算法

1.1 基于用户的协同过滤推荐算法（UserCF）

基于用户的协同过滤算法［10］是通过对隐式信息反馈，来预测用户对该物品的兴趣大小；通过对所有用户兴趣的浏览行为，来计算用户之间的相似性；对用户相似度进行排序，取相似度最高的前K个用户作为目标用户的邻域，根据邻域内的前K个用户的相似性特征，来预测目标用户对未访问过的物品的喜好程度；最后按照物品集合中的预测评分排列顺序，完成对目标用户的推荐。模型实现过程如下：

（1）用户-物品矩阵

假设有M个用户，N个项目，用户对项目评过分的历史行为设为1，未评过分的项目设为0，用户-物品矩阵如下：

其中，Rjk表示用户j对物品k是否有评分行为。

（2）为减少计算量，将用户-物品矩阵转化为统计有共同评分的倒排表，物品-用户倒排表如下：

其中，Wuv表示用户u与用户v共同评过分的物品数量。

（3）采用Jaccard 公式计算用户的相似度，如式（3）所示：

其中，Wuv含义同上所述；N（u）表示用户u评过分的物品集合；N（v）表示用户v评过分的物品集合；最终得到用户的相似度矩阵W。

（4）用户u对物品i的感兴趣程度用式（4）进行预测：

其中，S（u，K）表示与用户u相似度最接近的K个用户的集合；N（i）是对物品i有过评分行为的用户集合（即在对物品i有过评分行为的用户集合中找出与用户u相似度最接近的K个用户集合）；Wuv是用户u与用户v的相似度；Rvi表示用户v对物品i的评分行为。由于采用的是单一行为的隐式反馈数据，故令Rvi的值等于1。

（5）当所有预测完成后，对P（u，i）的结果进行降序排序，取前N个物品推荐给用户。

1.2 基于物品的协同过滤推荐算法（ItemCF）

基于物品的协同过滤算法是通过对隐式信息反馈来预测用户对该物品的兴趣大小，通过对所有物品的被浏览行为来计算物品之间的相似性，对物品相似度进行排序，取相似度最高的前K个物品并结合用户的行为，预测目标用户对未访问过的物品的喜好程度，最后按照物品集合中的预测评分完成对目标用户的推荐。模型实现过程如下：

（1）用户-物品矩阵

假设有M个用户，N个项目，用户对项目评过分的历史行为设为1，未评过分的项目设为0，用户-物品矩阵如式（1）。

（2）为减少计算量，将用户-物品矩阵转化为统计有共同爱好的倒排表，物品-用户倒排表如下：

其中，Cij表示物品i和物品j共同被喜欢的用户数量。

（3）采用Jaccard 公式（式（6））计算物品i与物品j的相似度，并用Wij表示用户的相似度矩阵。

其中，Cij表示物品-用户倒排表中记录的物品i与物品j被共同评过分的用户集合；N（i）表示物品i被评分过的用户集合；N（j）表示物品j被评分过的用户集合；最终得到用户的相似度矩阵W。

（4）用户u对物品j的感兴趣程度用式（7）进行预测。

其中，S（j，K）表示与物品j相似度最接近的K个物品的集合；N（u）是对用户u有过评分行为的物品集合；Wij是物品i与物品j的相似度；Rui表示用户u对物品i的兴趣。由于采用单一行为的隐式反馈数据，故当用户u对物品i有过评分行为时Rui ＝1。

（5）当所有预测完成后，对P（u，j）的结果进行降序排序，取前N个物品推荐给用户。

2 LFM 与SGD 算法

2.1 LFM 推荐算法

隐语义模型［11-12］（Latent Factor Model，LFM）推荐算法采用用户的历史行为数据来对用户进行相关内容推荐，是协同过滤（Collaborative Filtering，CF）推荐算法的一种。在协同过滤算法中，当用户或项目内容数量过多时，会导致用户-项目矩阵维度过大，且相关矩阵是稀疏的。LFM 算法的核心思想是矩阵分解（Matrix Factorization），其引入了一个隐式特征，将稀疏的用户-项目矩阵分解成相对稠密的用户-特征矩阵与特征-项目矩阵，极大的减少了空间复杂度。LFM 算法矩阵分解［13］原理如图1 所示。

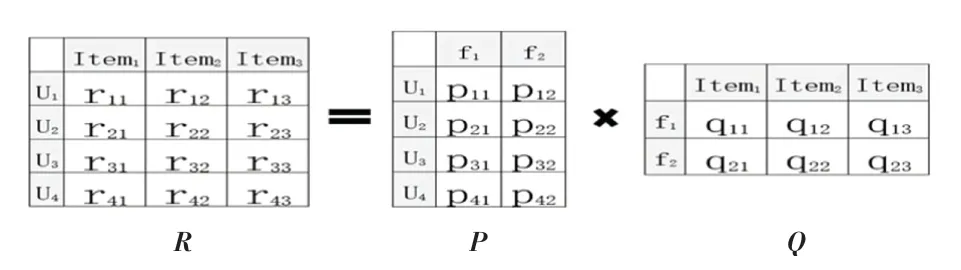
图1 LFM 矩阵分解原理Fig.1 LFM matrix decomposition schematic

如图1 所示，假设R是一个M ×N的用户-项目评分矩阵，LFM 算法的思想是要找到两个低维矩阵P、Q，同时引入一个隐式特征参F，如公式（8）所示，将用户-物品评分矩阵RM×N分解成用户-特征矩阵PM×F与特征-物品矩阵QF×N。

将被推荐用户记为u，推荐物品为i，则LFM 算法可通过公式（8）来预测用户u对物品i的感兴趣程度：

式中：F为隐式特征参数，Puf表示用户u与隐特征f的贡献度，Qfi表示隐特征f对物品i的贡献度，根据Predict（u，i）值的大小，从用户u对物品i的感兴趣程度排序高低，向用户推荐其感兴趣且未浏览过的物品。

2.2 SGD 算法

梯度下降［13-15］是迭代算法的一种，常用于求解最小二乘问题。在求解机器学习的模型参数，即无约束优化问题时，梯度下降是最常采用的方法之一。梯度下降的原理是通过对其求解损失函数的最小值，使用迭代的思想来求解，通过迭代得到最小化的损失函数和模型参数值。

假设有m个样本，其回归方程如式（9）、样本的损失函数如式（10）：

其中，hθ（xi）代表样本的实际值，yi表示对样本的预测值。分别对θ0和θ1求偏导：

得到两个变量的偏导数（即梯度后），根据负梯度的方向更新参数。重复更新的公式为：

其中，α为学习率。

假设一个用户-物品评分矩阵R是一个m × n矩阵，根据矩阵分解的思想，将一个大的稀疏矩阵分解成两个相对稠密的矩阵乘积，即矩阵R可以近似表示为P与Q的乘积：Rm×n ＝Pm×F ×QF×n。

将梯度下降的思想应用于矩阵当中，使用原始的用户-物品矩阵R（m，n）与预测评分矩阵R＇（m，n）之间的误差平方作为损失函数，即

其中，α是梯度下降的学习率。

2.3 改进的LFM-SGD 算法

2.3.1 算法设计

本文将隐式数据结合协同过滤推荐算法，利用隐语义模型（LFM）将原始的用户-物品矩阵分解成两个低维且数据稀疏性小的矩阵相乘，且将原始的用户-物品评分矩阵简化为没有用户评分的矩阵，即用户物品矩阵Ru×i中，用户u对物品i有过评分行为设为1，否则设为0。通过随机梯度下降（SGD）算法，预测用户对未接触过的物品喜好程度，取前N个物品进行推荐。该算法能有效缓解评分矩阵数据稀疏性的问题，在一定程度上提高了推荐的准确度。算法原理如图2 所示。

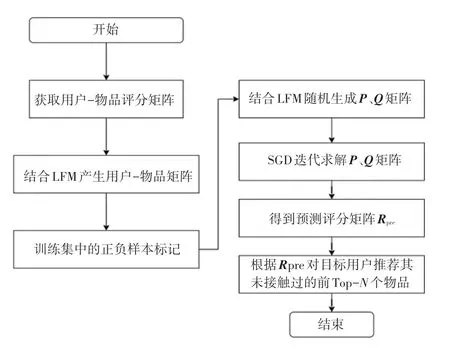
图2 整体算法原理图Fig.2 Overall algorithm schematic

2.3.2 SGD 优化算法

为优化算法拟合的结果，在求解最优解的同时防止过拟合，在损失函数式（15）中引入一个惩罚因子λ，将式（15）优化为

结合梯度式（13）、式（14），并按梯度方向更新向量式（16）、式（17），得到最终公式如下：

3 验证与分析

本文验证数据来源于美国Minnesota 大学GroupLens 网站提供的MovieLens-latest-small 数据集，数据集没有相关的电影内容简介。该数据集囊括100 836 条评分数据，610 个用户，9 724 部电影，3 683个标签。每个用户至少对20 部电影进行过评分，评分采用5 分制，以0.5 分为增量。测试集与训练集数量比例为1：6，且不采用显示评分数据。将用户有过行为的电影设置为1，没有则为0。

3.1 算法评估指标

本文采用准确率（Precision）、召回率（Recall）、覆盖率（Coverage）作为算法的评估指标。其中，准确率表示推荐项目列表中含有测试集中的数量与所有推荐项目数的比率；召回率表示用户推荐数量与测试集中用户有过行为的项目数的比率；覆盖率表示所有推荐项目数与总项目数的比率。假设A是正确预测的样本数量，B是测试集得到的所有用户的推荐样本数，C是测试集中所有用户有过历史行为的样本数，D是整个数据集中的样本数，则指标计算公式如下：

3.2 实验与结果分析

实验1分析模型超参数学习率α、正则化惩罚因子λ、隐式特征参数F、迭代数η对算法评估指标的影响。

由图3 可以看出，评估指标呈现先增大后减小的趋势。当学习率α为0.01 时Precision为20.915%，Recall为9.888%，Coverage为6.582%；由图4 可以看出，指标呈现先增大后平缓减小的趋势。当惩罚因子λ为0.01 时，Precision为20.015%，Recall为9.655%，Coverage为6.438%；当α、λ大于0.01 时，整体评估效果开始下降。

图3 学习率α 对评估指标的影响Fig.3 Influence of learning rate α on evaluation index

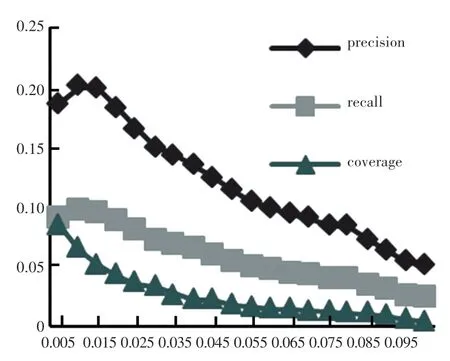
图4 惩罚因子λ 对评估指标的影响Fig.4 Influence of penalty factor λ on evaluation index

从图5 可以看出，隐式特征参数F的取值对整体评估的影响并不明显。当F ＝95 时，3 个指标取得局部最大值，Precision为20.401%，Recall为9.887%，Coverage为6.592%；而从图6 得知，随着迭代数η的增加，3 条曲线呈现缓慢上升随后平缓下降的过程。当迭代数η ＝30 时，Precision为20.066%，Recall为9.456%，Coverage为6.674%。

图5 隐式特征参数F 对评估指标的影响Fig.5 Influence of F on evaluation index

图6 迭代数η 对评估指标的影响Fig.6 Influence of η on evaluation index

综上所述，模型最终超参数设定为：α ＝0.01，λ ＝0.01，F ＝100，η ＝30。

实验2固定模型超参数，比较3 种算法的性能指标差异。

由图7 可知，融合LFM 的SGD 算法3 个指标均比基于用户（UserCF）和基于物品（ItemCF）的协同过滤推荐算法效果好。其覆盖率、召回率、准确率分别比UserCF 提高了0.761%、1.131%和3.175%，比ItemCF 提高了0.154%、1.388%、和3.898%。

图7 三种算法差异对比Fig.7 Comparison of the differences between the three algorithms

实验3将融合后的算法分别在ml-latestsmall 和ml-1m 数据集上验证。

从图8 可以看出，在更大规模的ml-1m 数据集上验证算法指标效果比小规模数据集更好。在一定程度上，改进的LFM-SGD 算法对大规模数据集效果更为显著。

图8 不同大小的数据集对比效果Fig.8 Comparison of data sets of different sizes

4 结束语

本文研究了基于隐语义模型的协同过滤推荐算法，使用了随机梯度下降预测对目标用户的推荐。通过隐式数据信息，并结合矩阵分解的思想，既优化了传统协同过滤推荐算法中冷启动的问题，也克服了数据规模大且稀疏的问题。实验结果验证了本文提出的算法较之其他算法的优势，改进的LFM＆SGD 算法的准确率、召回率、覆盖率均有显著提升，在缓解数据稀疏性、提高推荐精度方面取得了一定的成效。