基于特征不变量的三维点云数据交换密码水印算法研究

崔翰川 樊志辉

作者简介：崔翰川（1985— ），男，江苏盐城人，工程师，博士；研究方向：地理信息安全。

摘要：文章对三维点云数据的顶点模长特征进行了研究，提出了基于特征不变量的三维点云数据交换密码水印算法。利用三维点云数据的顶点模长集合在置乱加密过程中集合不变性，结合水印映射思想和奇偶量化的方式来嵌入水印信息。实验表明，算法保证了水印和加解密操作顺序的互换性，也提高了交换密码水印算法的耦合性、安全性和鲁棒性，为三维点云数据在实际传输、存储和使用过程中提供了安全保障。

关键词：三维点云数据；特征不变量；置乱加密；交换密码水印；数据安全保护

中图分类号：TP39 文献标志码：A

0 引言

我国正在加快构建新型基础测绘体系，全面推进实景三维中国建设。实景三维作为真实、立体、时序化反映人类生产、生活和生态空间的时空信息，是国家重要的新型基础设施。其中三维点云数据为刻画实景三维现实世界提供了最直接的表达方式，被普遍用于三维城市建模和智慧城市建设中，具有强烈的经济市场和安全保护需求［1］。

密码学技术和数字水印技术是当前地理信息安全领域较为成熟的技术，对三维点云数据的版权保护和安全传输有重要的作用［2］。密码学技术能够防止三维点云数据传输过程的泄密［3-4］，但无法对数据使用追踪，仅对三维点云数据安全保护起到事先防范的作用；数字水印技术能够实现三维点云数据使用过程的版权保護［5-6］，但无法防止传输过程的非法窃取，仅对三维点云数据的安全保护起到事后追责的作用［7］。交换密码水印（CEW）技术是将密码学和数字水印结合的新兴安全技术，为三维点云数据同时实现事先防范和事后追责提供安全保障［8］。目前，从CEW算法的实现机理上看，可分为基于分域、同态加密和不变特征的CEW算法3种方法。

基于分域的CEW是利用数学变换的方式将原始数据分离相互独立的两个区域［9-10］，选其中一部分进行加解密操作，另一部分进行水印嵌入和提取操作。Benrhouma等［11］对图像数据进行DWT变换，然后通过加密高频系数来实现数据的加密，最后在低频系数中嵌入水印信息，是一种较为经典的针对图像数据的CEW算法。该方法计算简单、效率快，但水印部分未受到密码学保护，算法的安全性不足。而利用同态加密自身特性［12-15］，密文数据的运算结果和明文数据运算结果一致，为CEW的实现提供了可靠的路径。Guo等［16］基于同态加密和DCT、DWT变换技术，通过替换变换域中的系数，实现了基于同态加密的CEW算法，解密和水印提取过程不需要暴露密文域和明文域，一定程度上提高了CEW算法的安全性。但基于同态加密普遍存在计算效率低、算法复杂的缺陷，难以应用到大数据量的三维点云数据。综合考虑CEW算法的安全性和可用性，Ren等［17］根据矢量数据的存储特征和组织结构，利用两个相邻多边形的内角和存储方向的特征不变性，并结合感知流密码坐标加密的方式实现CEW算法，该算法对常见的攻击具有一定的鲁棒性，并具备较高的安全性，但不适用于大数据量的点云数据。

综上分析，本文首先对三维点云数据的特征不变量进行分析，基于顶点模长特征值集合在置乱过程不变性，提出一种基于特征不变量的三维点云数据CEW算法。实现加密技术与水印技术在三维点云数据中的有机融合，并通过实验验证提出CEW算法的可行性，为三维点云数据在实际传输、存储和使用过程中提供安全保障。

1 三维点云数据特征不变量

三维点云数据是离散、不规则分布在三维空间中海量点的集合，由于三维点云数据没有稳定的排列顺序和拓扑结构，不具备矢量地理数据线面要素结构，因而没有模长、角度和面积等数据作为不变特征。若以点云数据的位置坐标作为不变特征，经过加密计算后，其特征极其容易发生变化，因此不能直接以点坐标来构建特征不变量。本文结合三维点云数据的自身特点，通过计算顶点坐标到三维点云数据重心的距离这一全局特征，构建三维点云数据的特征不变量，并作为交换密码水印算法的载体。假设某一顶点坐标为（x1，y1，z1），那么顶点到点云重心计算公式如下。

从式（1）可以得出，顶点模长特征值只与顶点到重心点距离有关，而距离值的大小不随平移、旋转、裁剪和置乱等操作而变换。因此，本文构建的三维点云数据特征不变量在常见的平移、旋转、裁剪和置乱等变换操作下具有不变性。

2 算法的实现

本文通过构建三维点云数据特征不变量，找寻数据中稳定不变的特征量来嵌入水印信息，并提出一种置乱偏移的加密算法，在保持顶点模长特征值不变的情况下实现对坐标值加密。在该方法中，首先通过球坐标转换得到的顶点模长和角度是两个相互独立的变量，且对顶点模长特征值集合置乱的过程并未改变其特征量的具体数值。因此，本文提出的基于特征值不变量的三维点云数据交换密码水印算法的加密和水印操作相互独立，互不干扰。

2.1 加密部分

三维点云数据顶点位置决定了点云数据形状，在三维点云数据中置乱加密算法结合三维点云数据海量性的特征，通过打乱数据原有的空间位置来提高对点云数据的加密效率，且加密后数据具备较高的隐蔽性。为提高对加密后数据的抗攻击能力，本文对数据的特征不变量置乱加密后，再对角度数据偏移加密，从而提高加密算法的安全性。其中加密部分算法步骤如下。

解密则是上述步骤的一个逆过程。

2.2 水印部分

在三维点云数据置乱偏移加密过程中，三维点云数据进行顶点模长特征集合的置乱加密，破坏了模长与角度之间的对应关系，但并未改变顶点模长的具体数值。因此，本文利用模长特征值集合置乱前后的不变性，采用奇偶量化的方式对模长特征值进行修改，并结合水印映射思想嵌入水印信息，具体步骤如下。

水印提取则是水印嵌入的逆过程。但值得一提的是，水印嵌入步骤和加密步骤的先后顺序可互换，即可先加密再嵌入水印，也可先嵌入水印再加密，得到相同的含水印密文数据，数据解密和水印提取过程顺序也可互换。

3 实验结果与分析

为了验证本文提出的交换密码水印方法的有效性，实验选用两个稠密程度和数据量不同的三维点云数据作为实验数据，分别记为数据A和数据B，如图1所示。其中，数据A中共计7 867 877个点，数据B中共计17 683 887个点。水印信息采用南京师范大学官网网址，编码为版本1、纠错能力H级、尺寸84×84的QR码，如图2所示。

为定量对已设计的CEW算法进行有效、科学的评价，通过均方误差（MSE）可以评价加密算法的安全性和水印的不可感知性。而归一化系数（NC）和误码率（BER）可以用来评价水印算法的鲁棒性，具体计算公式如下。

利用本文提出的CEW算法数据A和B进行水印嵌入和加密、水印提取和解密操作。如表1所示是含水印的密文数据，并计算两组数据坐标间的MSE结果。

由表1观察可知，水印嵌入和加密后破坏了原始点云数据的坐标位置和空间关系，无法从密文数据获取有用信息。且A和B数据加密前后MSE数值分别达到1 531.4 216和2 686.939 7。由此可知，本文所提的算法加密效果较好，具有一定的安全性。

采用解密密钥对上述密文数据进行解密，解密实验效果和MSE的计算结果如表2所示。

由表2可知，解密后的视觉效果与原始数据无明显差异，且两组数据解密前后的坐标几乎一致，表明CEW算法的加解密和水印操作是近无损的。

从解密后三维点云数据提取水印并扫码的结果如表3所示。

由表3可知，提取的QR码图像可以扫码识别出正确的水印信息，计算原始QR码和提取QR码的NC值均为1，BER值均为0，本文所提的CEW算法能够从解密后含水印数据准确提取水印信息。

3.1 可交换性

为验证本文提出的CEW算法中水印和密码学操作的可交换性，分别验证加密和水印嵌入操作的顺序、解密和水印提取操作顺序对实验结果的影响。对实验数据A和B先加密再嵌水印，得到含水印密文数据A1和B1，为了对比实验结果，再用同样的数据A和B先嵌水印再加密，得到含水印密文数据A2和B2，通过统计含水印密文数据的坐标值，并计算A1与A2、B1与B2的误差均值和方差，从而验证本文CEW算法的可交换性，实验结果如表4所示。

由表4可知，A1与A2、B1与B2误差的均值和方差均为0，由此可知加密和水印嵌入顺序不会影响实验结果，因此，本文的CEW算法加密和水印嵌入过程具备可交换性。

另一方面，本文CEW算法可交换还须考虑解密和水印提取的操作顺序，由于水印提取过程并不改动数据，因此，对含水印密文数据和含水印明文数据进行水印提取，通过计算提取水印信息的NC值和BER值为定量评价指标，来判断本文CEW算法在解密和水印提取过程中是否满足可交换性，提取结果如表5所示。

由表5可知，无论对含水印密文数据直接提取水印信息，还是先解密再提取水印信息，提取到的水印信息NC值均为1，BER值均为0。水印提取既可在密文数据中进行，也可在解密后明文数据中进行，解密和水印提取操作可互换。由此可知，本文提出的CEW算法的加解密操作和水印操作具备可交换性。

3.2 不可感知性

三维点云数据在水印嵌入的过程中，会对三维点云数据的坐标值进行改动，这必然会对高精度的三维点云数据造成一定影响。因此，对原始数据直接嵌入水印，和对含有水印密文数据解密得到含水印明文数据，分别记为数据A3和B3，并对这两组数据进行精度评价。含水印数据效果如图3所示。

从视觉直观上来看，原始数据与含水印信息数据无明显差异。客观上，通过计算两坐标之间的最大误差值、平均误差和标准差来统计不可感知性的指标，实验结果如表6、表7所示。

由上表的结果可以看出，不论是对A数据还是B数据，提出的CEW算法在X，Y，Z方向最大误差不到0.000 2 m，能够满足三维点云数据的空间精度要求，并且两组数据的标准差和平均误差都低于0.000 07 m，表示水印嵌入误差处于稳定状态，由此可知，本文提出的三维点云数据的CEW算法具备较好的不可感知性。

3.3 安全性

为了验证加密算法的安全性，通过加密算法和加密密钥对原始数据A和B加密得到密文数据A3和B3，再对原始密钥中末位值进行+1和-1的细微修改解密，得到解密数据并计算其MSE值，实验结果如表8所示。

由表8中解密后效果图和MSE值可知，即使对正确密钥做细微修改，解密后的数据也无法获取有用信息。因此，本文提出的CEW算法对密钥敏感性很高，提出的CEW算法具有很高的安全性。

3.4 鲁棒性

为了验证本文算法的鲁棒性，对含水印三维点云数据进行常见操作的攻击，再对遭受不同攻击后的数据进行水印提取实验，鲁棒性的评价指标以提取水印和嵌入水印的NC值和BER为准。

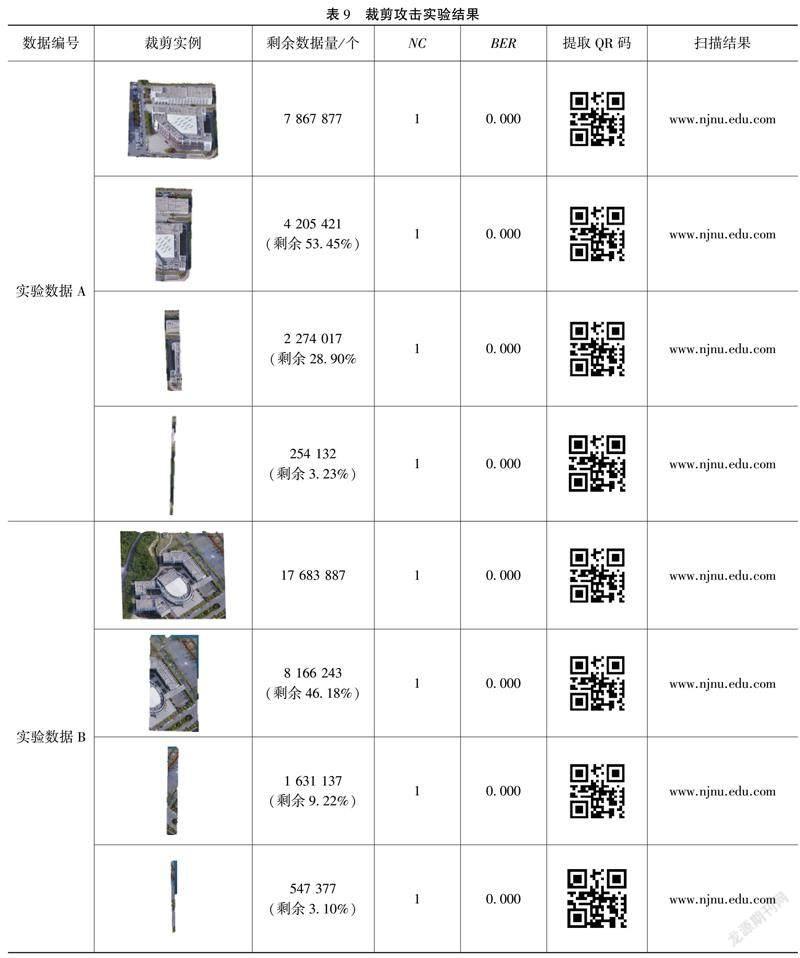
3.4.1 裁剪攻击实验

如表9所示，对三维点云数据的裁剪攻击由7 867 877和17 683 887个点数据裁至254 132（剩余3.23%）和547 377（剩余3.10%）个点，水印信息仍能被成功提取，且NC值均为1，BER均為0。实验表明，该算法在抵抗裁剪攻击中具有强鲁棒性。

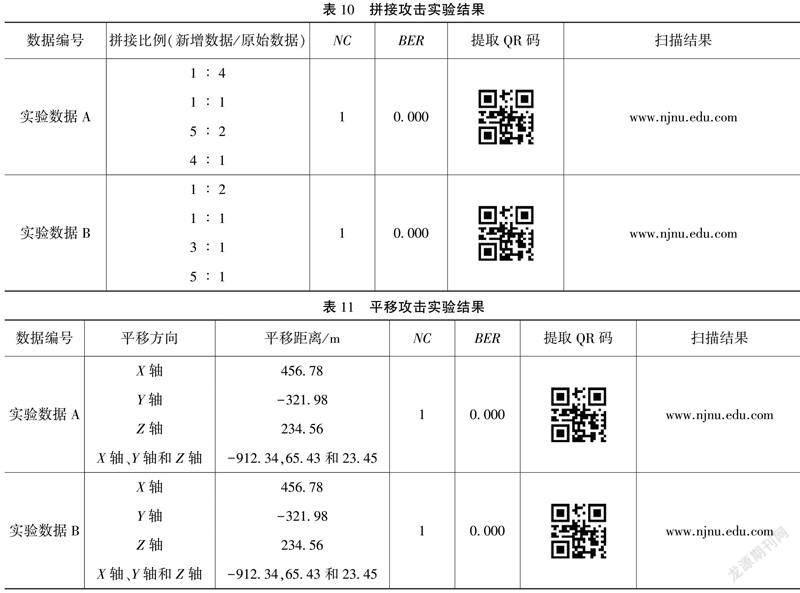
3.4.2 拼接攻击实验

如表10所示，对含水印数据进行不同程度的拼接，仍然可对拼接后的数据准确提取水印信息，并且计算提取水印信息与嵌入水印信息的NC值均为1，BER值均为0。实验表明，本文算法对拼接攻击具备强鲁棒性。

3.4.3 平移攻击实验

如表11所示，对数据进行任意方向和强度的平移操作，仍可以从遭受攻击后的数据成功提取水印信息。根据所提取水印信息与嵌入水印信息的NC值和BER值可知，本文算法可以抵抗任意方向的平移攻击。

4 结语

本文针对三维点云数据的自身特征，利用顶点模长特征值的不变性，提出了一种基于特征不变量的三维点云数据CEW算法，在保证密码和水印操作可交换的同时，兼顾了CEW算法的耦合性和鲁棒性，从而实现了对三维点云数据在存储、传输和使用过程中全方位的保护。实验结果表明，提出的三维点云数据CEW算法不仅满足CEW的基本性质和要求，还具备较强的安全性和耦合性，且对常见的点云数据攻击具备强鲁棒性。

参考文献

［1］杨必胜，梁福逊，黄荣刚.三维激光扫描点云数据处理研究进展、挑战与趋势［J］.测绘学报，2017（10）：1509-1516.

［2］朱长青.地理数据数字水印和加密控制技术研究进展［J］.测绘学报，2017（10）：1609-1619.

［3］JOLFAEI A， WU X， MUTHUKKUMARASAMY V.A 3D object encryption scheme which maintains dimensional and spatial stability［J］.IEEE Transactions on Information Forensics and Security， 2014（2）： 409-422.

［4］吴肇星，金鑫，宋承根，等.基于随机可逆矩阵的3D点云模型加密［J］.系统仿真学报，2016（10）：2455-2459.

［5］任娜，朱长青，王志伟.基于映射机制的遥感影像盲水印算法［J］.测绘学报，2011（5）：623-627.

［6］任娜，朱长青，佟德宇.改进的基于遥感影像线性亮度调整的水印检测算法［J］.南京师范大学学报，2014（3）：52-56.

［7］王刚，任娜，朱长青，等.倾斜摄影三维模型数字水印算法［J］.地球信息科学学报，2018（6）：738-743.

［8］蒋力.基于正交分解的交换密码水印技术研究［D］.武汉：武汉大学，2012.

［9］LIAN S， LIU Z， REN Z， et al.Commutative encryption and watermarking in video compression［J］. IEEE Transactions on Circuits and Systems for Video Technology， 2007（6）： 774-778.

［10］BATTISTI F，CANCELLARO M，BOATO G， et al.Joint watermarking and encryption of color images in the fibonacci-haar domain［J］.EURASIP Journal on Advances in Signal Processing， 2009（8）：28-40.

［11］BENRHOUMA O， MANNAI O， HERMASSI H.Digital images watermarking and partial encryption based on DWT transformation and chaotic maps：2015 IEEE 12th International Multi-Conference on Systems， Signals & Devices （SSD15） ［C］.Mahdia：IEEE， 2015.

［12］ZHANG X.Commutative reversible data hiding and encryption［J］.Security and Communication Networks， 2013（11）： 1396-1403.

［13］李玉，張黎明，王昊，等.运用同态加密的高分遥感影像交换密码水印算法［J］.激光与光电子学进展，2022（18）：319-328.

［14］李增鹏，马春光，周红生.全同态加密研究［J］.密码学报，2017（6）：561-578.

［15］方立娇.基于同态的交换加密水印算法研究与实现［D］.北京：北京印刷学院，2021.

［16］GUO J，ZHENG P，HUANG J.Secure watermarking scheme against watermark attacks in the encrypted domain［J］.Journal of Visual Communication and Image Representation， 2015（30）： 125-135.

［17］REN N，ZHU C，TONG D， et al.Commutative encryption and watermarking algorithm based on feature invariants for secure vector map［J］.IEEE Access， 2020（8）：221481-221493.

（编辑 沈 强）

Abstract： Researching on Vertex modulus feature of 3D point cloud data， an exchange cryptographic watermarking algorithm based on feature invariants for 3D point cloud data is proposed. Using set invariance of the vertex moduli set in the scramble encryption process of the 3D point cloud data， the watermark information is embedded by combining the watermark bitmap and parity quantization. Experiments show that the algorithm ensures the interchangeability of watermarking and operation sequences of encryption and decryption， and also improves the coupling， security and robustness of the exchange cipher watermarking algorithm， providing a better security solution for the actual transmission， storage and use of 3D point cloud data.

Key words： 3D point cloud data; feature invariant; scramble encryption; exchange cryptographic watermarking; data security protection