基于PSO-SVR模型的河南省小麦产量预测方法

刘合兵 王垒 王一飞 席磊

摘要：小麦生产是河南省农业生产中的重要环节，在维持粮食供应和安全方面发挥着重要作用。对小麦产量进行准确预测可以为农业经济调控、政策制定提供重要性信息。为提高小麦产量预测精度，综合考虑影响小麦产量的相关因素，基于皮尔逊相关系数分析特征变量与产量之间的相关性。选取支持向量回归（support vector regression，SVR）模型解决小麦估产中的复杂性、非线性及小样本等问题。引入粒子群算法（particle swarm optimization，PSO）对SVR模型的惩罚因子（c）和核参数（g）进行优化，提高SVR模型的预测精度。以河南省1978—2019年小麦产量数据及其特征变量数据构建数据集，并与BP、Elman等神经网络模型及优化模型进行对比仿真试验。结果表明，PSO对SVR模型的优化效果明显高于传统的神经网络，PSO-SVR模型预测结果的4项评价指标均优于其他模型。其中，PSO-SVR模型的平均绝对百分比误差MAPE为0.87%，与SVR模型相比误差降低了57.4%、与PSO-BP模型相比误差降低了64.8%。PSO-SVR模型能够提高小麥产量预测精度，稳定性好，可为小麦产量预测提供新的思路与方法，具有较好的应用推广价值。

关键词：小麦产量预测；粒子群算法；SVR；BP；Elman

中图分类号：S126 文献标志码：A

文章编号：1002-1302（2023）08-0157-07

基金项目：河南省科技攻关计划（编号：212102110204、222102110234）；河南省现代农业产业技术体系（编号：S2010-01-G04）；河南省研究生教育改革与质量提升工程项目（编号：YJS2023AL046）。

作者简介：刘合兵（1972—），男，河南台前人，硕士，副教授，硕士生导师，主要从事数据挖掘方面的研究。E-mail：liuhebing@henau.edu.cn。

通信作者：席 磊，硕士，教授，主要从事分布计算与智能系统研究。E-mail：hnaustu@126.com。

农业是河南省的基础产业，小麦是基础中的核心，关系着河南省的经济命脉。小麦产量可看成是生育期内气象条件、土壤条件、地理环境、物候信息、生长发育状况等多个影响因素相互叠加的结果，具有复杂性、非线性以及小样本等特性，针对其预测存在一定难度。

现有的小麦产量预测大致可分为以下3类：一是利用历史特征统计资料建立统计回归模型；二是利用气象数据建立气象因子模型；三是利用遥感数据建立作物模拟模型。作物模拟模型可以提供对生理过程的深入理解并反映作物与环境变量之间的相互关系，但将模型用于产量模拟之前通常需要在局部范围内对大量的实地观察数据进行校准和验证，因此阻碍了它们的大规模应用［1］。气象因子模型能够详细分析各因素在不同生育期对作物产量的影响程度［2］，可以为作物生产提供指导性意见。但模型运用前期需要对天气数据、干旱数据、温度数据、降水数据等大量气象数据进行收集与整编，不仅需要投入大量时间而且还需要具备专业的气象知识。与作物模拟模型和气象因子模型相比，统计回归模型［3］具有成本低、数据易收集、易于运用等特点，因此被广泛应用于作物产量预测。

小麦产量预测一直是国内研究中的热点，相比于国际上较为流行的气象因子预测［4-5］、遥感技术预测［6-7］以及作物生长机理模型预测［8-9］等方法，国内关于小麦产量的预测大部分是建立在农业生产统计资料［10-11］基础上的。林滢等选择不同生长阶段的数据，基于随机森林算法采用遥感、土壤、气候数据进行训练确定了河南省产量预测的最佳时间段［12］。王来刚等基于随机森林算法对河南省大尺度多源时空数据进行分析，不仅得出了有关小麦产量的重要影响因素，而且构建了不同生长阶段的模型并探讨模型的预测精度［13］。刘峻明等基于随机森林算法结合气象数据，使用气象产量、相对气象产量、单产来预测河南省冬小麦产量［14］。曾妍等建立冬小麦各生育期的条件植被温度指数（VTCI）、叶面积指数（LAI）与冬小麦产量之间的支持向量回归模型对陕西省关中平原的5个市进行产量预测［15］。赵桂芝等基于混沌理论对原始数据进行相空间重构，再用PSO算法优化SVM参数，对粮食产量进行仿真试验并取得了较高的预测精度［16］。高心怡等通过对粒子群算法添加变异交叉机制以及族外竞争机制来优化支持向量回归模型对我国粮食产量进行预测［17］。李晔等结合灰色模型和马尔可夫理论，基于新信息优先的思想建立了新维无偏灰色马尔可夫模型提高了小麦产量预测精度［18］。Ali等开发了一个结合马尔可夫链蒙特卡罗（MCMC）Copula技术的混合遗传规划模型，建立了几种不同类型的GP-MCMC-copula模型，每种模型都具有著名的copula族，以筛选当前研究区域的最佳棉花产量预测模型［19］。马创等利用马尔可夫模型，对灰色模型的预测值进行残差修正，实现了对粮食产量的周期性预测［20］。赫晓慧等利用CNN从多光谱遥感影像中提取空间-光谱特征，结合GRU从遥感影像中自适应学习冬小麦生育期的时间依赖对其产量进行回归预测［21］。刘鹏等将历史产量和气候因素相结合，使用LSTM模型以固定年份为单位对下一年农作物产量进行预测［22］。胡程磊等以粒子群为基础，引入繁殖和变异机制优化神经网络的权值阈值，提高了产量预测的精度［23］。

支持向量回归模型是一种专门针对小样本问题的非线性回归模型［24］，可以归结为求解凸二次规划问题，理论上可以得到全局最优解。本研究为提高小麦产量预测精度，在支持向量回归模型中引入粒子群优化算法，利用河南省小麦产量数据及其特征变量数据进行仿真试验。

1 材料与方法

1.1 数据来源

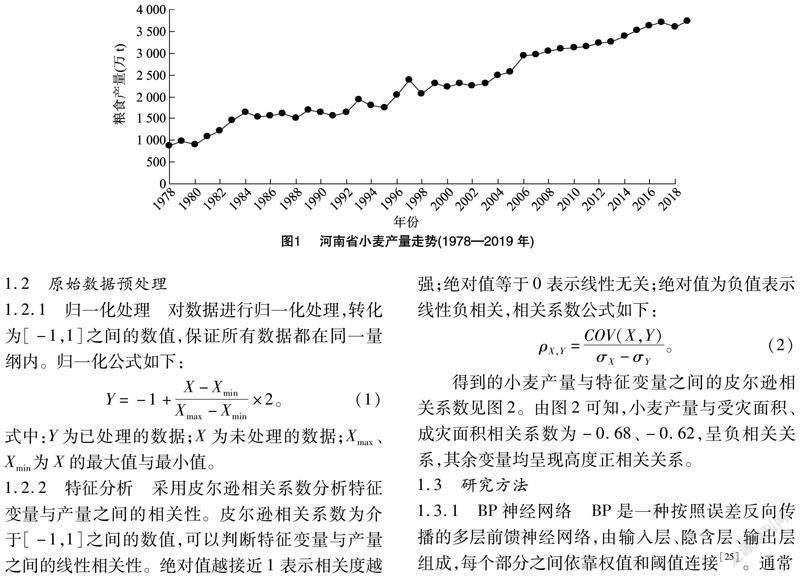
本研究数据来源于河南省统计年鉴及国家统计局年度数据。以河南省1978—2019年小麦产量数据构建输出指标，以小麦播种面积、粮食播种面积、耕地面积、农用机械总动力、灌溉面积、化肥施用折纯量、农村用电量、小麦单位面积产量、受灾面积、成灾面积、农业总产值11个特征变量构建输入指标体系，河南省小麦产量走势见图1。由图1可知，河南省小麦产量整体呈上升趋势，个别年份呈下降趋势且具有一定的波动性。

1.2 原始数据预处理

1.2.1 归一化处理

对数据进行归一化处理，转化为［-1，1］之间的数值，保证所有数据都在同一量纲内。归一化公式如下：

式中：Y为已处理的数据；X为未处理的数据；Xmax、Xmin为X的最大值与最小值。

1.2.2 特征分析

采用皮尔逊相关系数分析特征变量与产量之间的相关性。皮尔逊相关系数为介于［-1，1］之间的数值，可以判断特征变量与产量之间的线性相关性。绝对值越接近1表示相关度越强；绝对值等于0表示线性无关；绝对值为负值表示线性负相关，相关系数公式如下：

得到的小麦产量与特征变量之间的皮尔逊相关系数见图2。由图2可知，小麦产量与受灾面积、成灾面积相关系数为-0.68、-0.62，呈负相关关系，其余变量均呈现高度正相关关系。

1.3 研究方法

1.3.1 BP神经网络

BP是一种按照误差反向传播的多层前馈神经网络，由输入层、隐含层、输出层组成，每个部分之间依靠权值和阈值连接［25］。通常情况下增加隐含层可以降低模型误差，但也会使网络结构变复杂，训练时间变长，甚至出现过拟合现象。单隐含层BP神经网络在上述矛盾中可实现较好平衡，产生过拟合倾向较小，其拓扑结构见图3。

BP神经网络的结构模型，其输入、输出关系如式（3）所示：

1.3.2 Elman神经网络

Elman为4层结构（包括输入层、承接层、隐含层及输出层），承接层［26］用来存储隐含层前一时间的输出数据，并返回给该网络输入，增强了神经网络的处理能力。其拓扑结构见图4［27］。

Elman神经网络的结构模型，其输入、输出关系见式（4）～式（6）。

1.3.3 BP、Elman隐含层节点个数的确定

隐含层节点数是导致“过拟合”的直接原因，隐含层节点数与输入输出向量维度相关，并且每个模型节点个数都是不一样的［28］。常用的计算公式如式7所示。

式中：k为隐含层节点数，p为输入层节点数，b为输出层节点数，n为1～10之间的常数。利用整个节点空间中的每1个节点进行验证计算，具体结果见表1所示。

由表1可知，Elman神经网络隐含层节点个数为13时模型平均绝对误差（MAE）最小为200.36，效果最好。BP神经网络隐含层节点个数为8时模型平均绝对误差（MAE）最小为119.14，效果最好。

1.3.4 支持向量回归模型

为了解决回归拟合的问题，Cortes等在SVM分类的基础上引入ε线性不敏感损失函数，得到了SVR模型［29］，结构见图5。

支持向量回归将高维空间内积运算化简成了从低维空间进行输入的核函数计算，核函数的类型决定了SVR的不同特性，从某种程度上直接影响着模型的预测精度［30］。常用的核函数有：

由于PSO寻优时不调整参数、收敛更快、操作更加简单、精度更高，因此采用粒子群算法优化支持向量回归模型，提升模型效率。PSO-SVR模型的运行过程见图6。

模型具體步骤如下：

第1步：划分数据集，归一化处理，输入数据。

第2步：建立初始SVR模型，设置5折交叉验证。

第3步：使用训练集数据训练模型，设置PSO初始参数、目标精度（ε）、最大迭代次数（k）等，生成粒子的速度与位置。

第4步：将每个粒子所寻的最优c（bestc）和最优g（bestg）带入模型中，得出预测值，确定粒子的适应度值，为预测值与真实值的均方误差。

第5步：将粒子的适应度值与Pbest的适应度值进行比较，若更好则代替为Pbest，同理更新gbest。

第6步：是否满足终止条件（适应度值<ε或迭代次数>k）满足则输出最优c、最优g，反之，不断更新粒子的位置和速度，返回步骤4。

第7步：用最优c和最优g代替SVR模型中的c和g。

第8步：对比不同类型核函数的PSO-SVR模型，选择精度最高的核函数构建PSO-SVR模型。

第9步：将测试集数据带入训练好的模型中，计算预测精度。若不满足回到步骤3，满足则输出最终预测结果。

PSO-BP模型［32-33］、PSO-Elman［34-35］模型的具体优化步骤与PSO-SVR模型方式一致，不再进行重复描述。

2 结果与分析

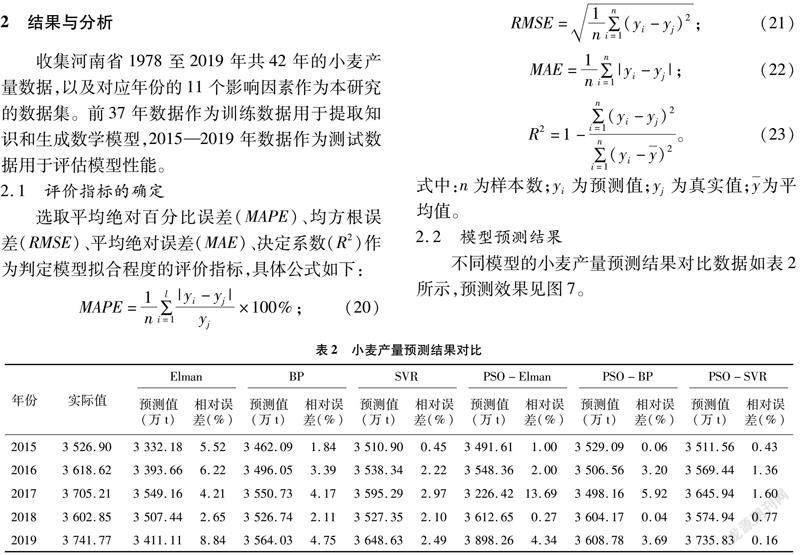
收集河南省1978至2019年共42年的小麦产量数据，以及对应年份的11个影响因素作为本研究的数据集。前37年数据作为训练数据用于提取知识和生成数学模型，2015—2019年数据作为测试数据用于评估模型性能。

2.1 评价指标的确定

选取平均绝对百分比误差（MAPE）、均方根误差（RMSE）、平均绝对误差（MAE）、决定系数（R2）作为判定模型拟合程度的评价指标，具体公式如下：

2.2 模型预测结果

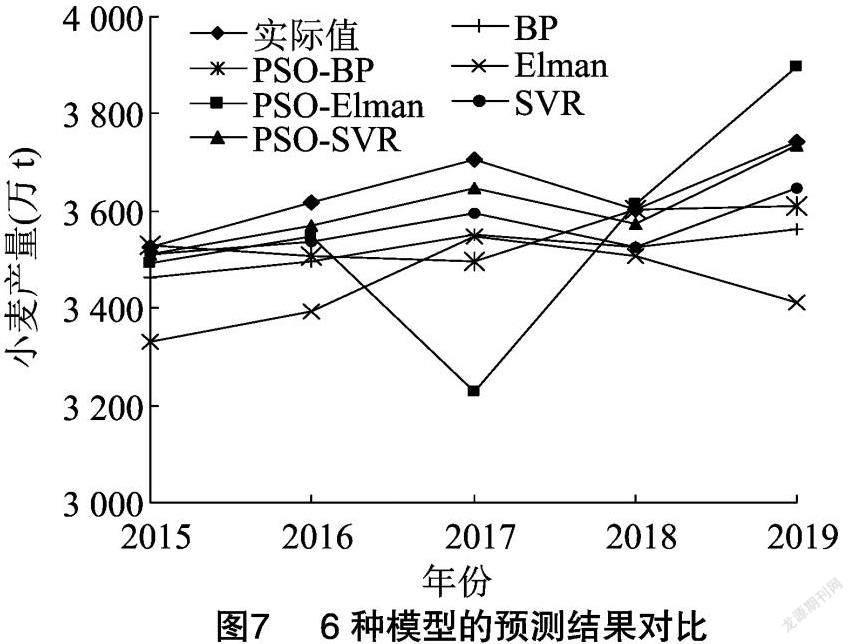
不同模型的小麦产量预测结果对比数据如表2所示，预测效果见图7。

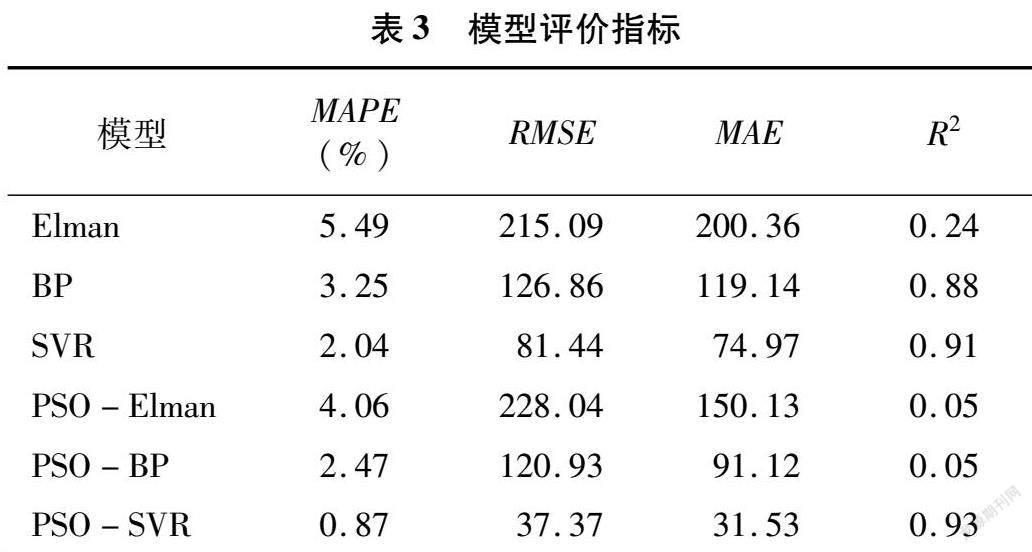
由表3可知，Elman、PSO-Elman、BP、PSO-BP模型的特点在于预测结果不稳定，容易陷入局部最小值。SVR模型的稳定性较好，但总体预测效果有待提高。PSO-SVR模型较SVR模型不仅精度有明显的提高，预测效果也较稳定。

MAPE是一项反映预测方法总体有效性的指标，PSO-SVR模型MAPE为0.87%，远小于其他模型，说明粒子群优化算法的全局搜索能力对SVR模型参数的优化效果更优。RMSE反映的是误差分散程度 PSO-SVR模型的RMSE为37.37 远小于其他模型，说明PSO-SVR模型的拟合效果更稳定。

MAE反映的是预测误差绝对值的均值，其值反映精度大小，PSO-SVR模型的MAE为31.53，远小于其他模型，说明PSO-SVR模型的精度最高。R2反映的是回归拟合曲线的拟合优度，PSO-SVR模型的R2为0.93（表3），大于其他模型，说明粒子群优化算法对SVR模型的回归拟合效果最优。

3 结论与讨论

针对小麦产量预测的复杂性、非线性及小样本等特性，在选取的SVR模型及传统的神经网络模型基础上，采用PSO优化算法对3种模型参数进行优化，并结合河南省实际小麦产量数据进行仿真试验。试验结果表明，SVR模型在小麦产量预测上具有很大的潜力，PSO-SVR模型的预测精度及拟合效果明显优于其他模型，为小麦产量预测提供了新的思路与方法。

特征变量的选取能影响模型的预测效果。下一步工作将在现有数据集上扩充气象因素（如日照时间、有效积温、降水量、温度等），进一步优化小麦产量预测模型，提高模型预测精度，以期为农业生产提供指导。

参考文献：

［1］Fayaz A，Kumar Y R，Lone B A，et al. Crop simulation models：a tool for future agricultural research and climate change［J］. Asian Journal of Agricultural Extension，Economics & Sociology，2021：146-154.

［2］Xu X Y，Gao P，Zhu X K，et al. Design of an integrated climatic assessment indicator （ICAI） for wheat production：a case study in Jiangsu Province，China［J］. Ecological Indicators，2019，101：943-953.

［3］Qiming Z，Ali I. Integration of maximum crop response with machine learning regression model to timely estimate crop yield［J］. Geo-spatial Information Science，2021，24（3）：474-483.

［4］吴冰洁，王 靖，唐建昭，等. 华北平原冬小麦产量变异的气象影响因子分析［J］. 中国农业气象，2018，39（10）：623-635.

［5］Ruan G J，Li X Y，Yuan F，et al. Improving wheat yield prediction integrating proximal sensing and weather data with machine learning［J］. Computers and Electronics in Agriculture，2022，195：106852.

［6］王飞龙，王福民，胡景辉，等. 基于相对光谱变量的无人机遥感水稻估产及产量制图［J］. 遙感技术与应用，2020，35（2）：458-468.

［7］Franch B，Vermote E F，Skakun S，et al. Remote sensing based yield monitoring：application to winter wheat in United States and Ukraine［J］. International Journal of Applied Earth Observation and Geoinformation，2019，76：112-127.

［8］余新华，赵维清，朱再春，等. 基于遥感和作物生长模型的多尺度冬小麦估产研究［J］. 光谱学与光谱分析，2021，41（7）：2205-2211.

［9］Xie Y，Huang J X. Integration of a crop growth model and deep learning methods to improve satellite-based yield estimation of winter wheat in Henan Province，China［J］. Remote Sensing，2021，13（21）：4372.

［10］陈全润，杨翠红. 河南省粮食产量预测方法研究［J］. 系统科学与数学，2018，38（7）：813-822.

［11］姜 新. 河南省粮食产量影响因素和预测方法研究［J］. 中国农学通报，2019，35（1）：154-158.

［12］林 滢，邵怀勇. 基于随机森林算法的河南省冬小麦产量预测最佳时间窗和影响因子研究［J］. 麦类作物学报，2020，40（7）：874-880.

［13］王来刚，郑国清，郭 燕，等. 融合多源时空数据的冬小麦产量预测模型研究［J］. 农业机械学报，2022，53（1）：198-204，458.

［14］刘峻明，和晓彤，王鹏新，等. 长时间序列气象数据结合随机森林法早期预测冬小麦产量［J］. 农业工程学报，2019，35（6）：158-166.

［15］曾 妍，王 迪，赵小娟. 基于支持向量回归的关中平原冬小麦估产研究［J］. 中国农业信息，2019，31（6）：10-20.

［16］赵桂芝，赵华洋，李 理，等. 基于混沌-SVM-PSO的粮食产量预测方法研究［J］. 中国农机化学报，2019，40（1）：179-183.

［17］高心怡，韩 飞. 基于混合智能算法的支持向量机的粮食产量预测［J］. 江苏大学学报（自然科学版），2020，41（3）：301-306.

［18］李 晔，白 雪. 基于新维无偏灰色马尔可夫模型的小麦产量预测［J］. 江苏农业科学，2021，49（15）：181-186.

［19］Ali M，Deo R C，Downs N J，et al. Cotton yield prediction with Markov Chain Monte Carlo-based simulation model integrated with genetic programing algorithm：a new hybrid copula-driven approach［J］. Agricultural and Forest Meteorology，2018，263：428-448.

［20］马 创，袁 野，尤海生. 基于灰色——马尔可夫模型的农产品产量预测方法［J］. 计算机科学，2020，47（S1）：535-539.

［21］赫晓慧，罗浩田，乔梦佳，等. 基于CNN-RNN网络的中国冬小麦估产［J］. 农业工程学报，2021，37（17）：124-132.

［22］刘 鹏，郑 勇，杨红军. 基于改进神经网络的农作物产量预测方法［J］. 电子技术应用，2019，45（10）：88-91，99.

［23］胡程磊，刘永华，高菊玲. 基于IPSO-BP模型的粮食产量预测方法研究［J］. 中国农机化学报，2021，42（3）：136-141.

［24］郝晓露，张姗姗，朱家明. 基于模糊時序的SVR模型对空气质量的预测［J］. 兰州文理学院学报（自然科学版），2019，33（4）：17-23，39.

［25］刘 阳，谭凯旋，郭钦鹏，等. 运用随机森林和GA-BP神经网络预测岩石爆破块度［J］. 矿业研究与开发，2021，41（1）：135-140.

［26］Liu B，Wu Q L，Cao Q. An improved Elman network for stock price prediction service［J］. Security and Communication Networks，2020，2020：8824430.

［27］周 鹤. 基于改进Elman神经网络的水稻生长预测［D］. 扬州：扬州大学，2019.

［28］王嵘冰，徐红艳，李 波，等. BP神经网络隐含层节点数确定方法研究［J］. 计算机技术与发展，2018，28（4）：31-35.

［29］Cortes C，Vapnik V. Support-vector networks［J］. Machine Learning，1995，20（3）：273-297.

［30］杜彦斌，胡言峰，许 磊，等. 基于PSO-SVR的15-5PH合金粉末激光熔覆层稀释率预测方法［J］. 计算机集成制造系统，2022，28（7）：2169-2178.

［31］Kennedy J，Eberhart R. Particle swarm optimization［C］//Proceedings of ICNN95-International Conference on Neural Networks.Perth：IEEE.：1942-1948.

［32］郭亚菲，樊 超，闫洪涛. 基于主成分分析和粒子群优化神经网络的粮食产量预测［J］. 江苏农业科学，2019，47（19）：241-245.

［33］杨冬梅，李竹一，张健楠，等. 基于PSO-BP神经网络的工业装备造型设计研究［J］. 机械设计，2021，38（7）：126-132.

［34］赵丽清，段东瑶，殷元元，等. 基于PSO-Elman算法的茶叶烘干含水率预测［J］. 农业工程学报，2021，37（19）：284-292.

［35］邹 浩，窦震海，张 博，等. 基于提升小波和改进PSO-Elman神经网络的短期负荷预测［J］. 电测与仪表，2020，57（21）：119-125.