基于多重分形关联和深度CNN的常规雷达目标分类方法

李秋生,朱化娟,胡俊勇

(1.赣南师范大学 智能控制工程技术研究中心,江西 赣州 341000;2.赣南师范大学 物理与电子信息学院,江西 赣州 341000)

现代信息化战争对雷达性能提出了较高要求,要求雷达不仅能探测目标,还能提供目标类别和类型等信息.常规低分辨率雷达在远程警戒、隐身目标探测等领域,发挥了不可替代的作用.然而,受工作带宽窄、脉冲重复频率低的限制,常规低分辨率雷达难以对探测目标进行识别分类.作为常规低分辨率雷达监测的一类重要目标,飞机并非刚体,它们的结构和材料组成复杂,其机翼抖动、机身颤振会对回波幅度、相位产生复杂的非线性调制[1].此外,飞机的旋转部件对雷达电磁波产生的喷气引擎调制(jet engine modulation,简称JEM)也是非线性的,且与飞行姿态角无关[2].提取这些反映飞行器物理特性的非线性调制特征,对飞机目标的识别分类具有重要意义.

在低分辨率雷达空中目标识别分类中,一般使用点目标模型进行分析,通过JEM效应识别目标.目标旋转部件的往复运动对雷达回波产生周期性调制,且不同旋转部件产生的调制是不同的.常见的JEM特征提取方法有:复倒谱、AR(autoregression)模型功率谱[3]、SVD(singular value decomposition)特征值分解法[4]等.这些提取方法大多侧重于谱线间隔的估计,计算复杂,需要较高的脉冲重复频率和较长的观测时间,因此这些方法的准确率不高[5].为了解决上述问题,研究人员进行了大量相关研究.文献[6]利用分数布朗运动构建了飞机回波模型,提出了一种基于分数布朗维数特征的分类方法.文献[7]将多重分形理论引入低分辨率雷达飞机回波的特性分析和特征提取.文献[8]提出了一种基于集合经验模态分解和多重分形的飞机分类方法,先使用集合经验模态分解重构目标的回波微动分量,后对回波微动分量进行多重分形特性分析和特征提取,实现了对民航机和战斗机等目标的分类.多重分形关联扩展了多重分形的“单点”统计特性,考虑了空间相关的特征奇异指数,相对于多重分形能提供更多的信息.文献[9]将多重分形关联应用到常规雷达目标回波的特性分析和特征提取中,取得了较好的分类效果.文献[10]引入分数阶Fourier变换对飞机回波进行处理,找到了最优变换阶数,在最优分数阶Fourier域对目标回波进行多重分形关联特性分析和特征提取,分类准确率得到了较大的提升.

上述研究虽取得了一定的成果,但均是基于先验知识寻找相应特征,故存在以下不足:①由于每类目标都有自己的特征,当目标发生变化时,需对特征进行重新定制;②在定义特征的过程中,如果不够合理,会对实验结果产生很大的影响.近年来,基于卷积神经网络(convolutional neural network,简称CNN)等深度学习网络的目标分类技术得到快速发展,并应用于目标分类领域[11].文献[12]针对复杂噪声与杂波环境下传统分类方法效率低且准确率不高的问题,提出了基于残差连接长短期记忆网络(long short term memory,简称LSTM)的雷达目标分类模型.文献[13]将CNN模型用于SAR(synthetic aperture radar)图像目标分类,提高了SAR图像分类的泛化性和准确性.文献[14]针对散斑噪声随机性、训练数据姿态缺失等问题,将深度CNN与数据增强相结合,提升了SAR目标分类的能力.该文拟提出一种基于多重分形关联特征和深度CNN的飞机分类方法,以提高不同类型飞机的分类准确率.

1 多重分形关联理论

1.1 多重分形关联

多重分形通过对分形体几何支集上所有点的奇异指数做统计分析,确定多重分形谱[15].多重分形关联是多重分形的推广,相对于多重分形,能反映更多的自相似信息[16].

把分形几何体分成若干小区域,小区域的测度分布概率[17]为

Pσ(ε)=εσ,

(1)

其中:σ为奇异指数,ε(ε<1)为小区域的尺度大小.

几何体的分形维数[17]为

(2)

其中:Nε为小区域总数.

由式(2)可得

Nε=ε-D0.

(3)

由式(1)～(2)可得

Pσ(ε)=εD0-f(σ),

(4)

其中:f(σ)表示多重分形奇异谱.

(5)

其中:Pε(σ1,σ2,d)表示在相距为d的两个位置观测到两个奇异指数的联合概率,σ1和σ2为同一尺度下的2个奇异指数;ω=lnd/lnε.

在随机乘法过程产生的不连续测度基础上,结合文献[17]对多重分形关联谱的推论,可得

(6)

其中

φ(q1,q2)=min{φ(q1,q2),1}=min{τ(q1,q2)-τ(q1)-τ(q2)-D0,1},

(7)

其中:q1和q2均为权重.

1.2 多重分形关联谱

多重分形关联谱包含更多目标回波的空间特征,能更好地反映不同目标间的差异.以飞机向站飞行姿态下的实测回波数据为例,图1(a)～(c)分别给出了3类飞机多重分形关联谱的投影图.从图1可看出,不同类型飞机目标的多重分形关联谱的投影图存在明显差异,可用于目标分类.

图1 3类飞机多重分形关联谱的投影图

2 深度CNN

深度CNN包括卷积层、池化层和全连接层[18].假设输入图像大小为w1×h1,卷积核大小为k×k,stride为S,图像深度为c1,padding为p.卷积输出图像的大小为w2×h2,图像深度为c2.输入图像与卷积输出图像参数间的关系为

h2= (h1-k+2p)/S+1,

(8)

w2=(w1-k+2p)/S+1,

(9)

c2=c1.

(10)

池化输出图像的相关参数为

W2=(W1-F)/S1+1,

(11)

H2=(H1-F)/S1+1,

(12)

其中:W1,W2分别为原始图像宽度、池化后的图像宽度;H1,H2分别为原始图像高度、池化后的图像高度;F为卷积核的宽度;S1为步幅.

全连接层的输出[19]为

y=Wx,

(13)

其中:W是权重矩阵,x为输入矩阵.全连接层的一个功能是维度转换,另一个功能是潜在因子表达,将原始特征映射至每个潜在因子节点.全连接层中的最后一层是分类的显性表达.

Resnet-50网络模型[20]是一种深度CNN模型,其中的残差模块可解决梯度消失和训练参数优化问题.Resnet-50网络模型的部分结构如图2所示.

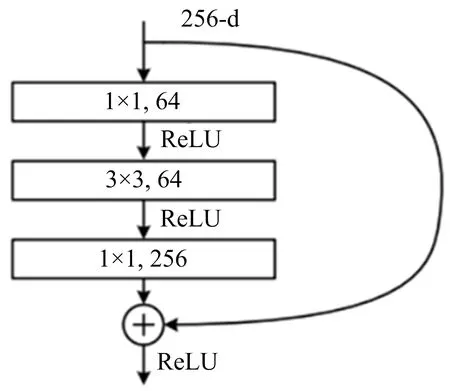
图2 Resnet-50网络模型的部分结构

3 方法流程

图 3为该文提出的基于多重分形关联特征和深度CNN的常规雷达目标分类方法的流程.

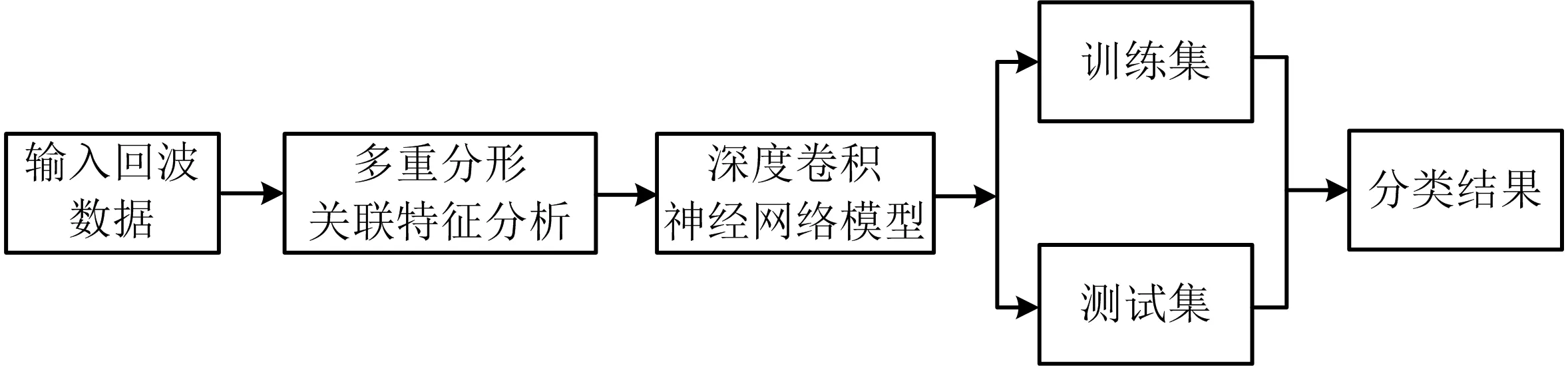
图3 基于多重分形关联特征和深度CNN的常规雷达目标分类方法的流程

基于多重分形关联和深度CNN的常规雷达目标分类方法的具体步骤为:

(1) 对飞机雷达回波信号进行多重分形关联分析,得到多重分形关联谱.

(2) 将多重分形关联谱的投影图作为特征图.

(3) 将特征图分为训练集和测试集,并微调超参数.

(4) 使用训练后的模型对目标进行分类.

4 实 验

4.1 实验数据

该文实验数据来自国产警-17雷达上采集的大型民航机、小型民航机和战斗机等目标回波数据.实验数据由5 760组回波数据组成,表1给出了实验数据,其中第1～3类飞机的飞行姿态为向站,第4～6类飞机的飞行姿态为背站.

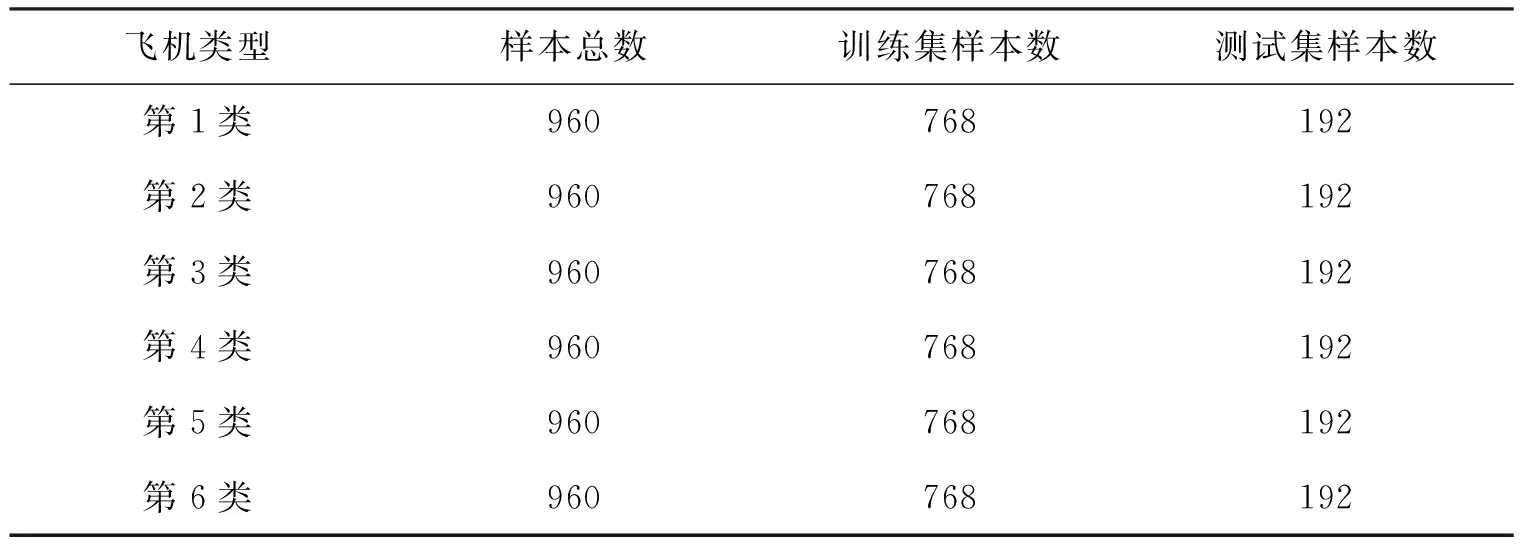
表1 实验数据

4.2 实验指标及相关物理量

实验有4个指标:真阳性(TP)、假阳性(FP)、假阴性(FN)、真阴性(TN)[21].

分类准确率的表达式为

(14)

受试者操作特征(receiver operating characteristic curve,简称ROC)曲线能反映受测对象敏感性与特异性间的关系[22],其水平和垂直坐标分别为

TPR=TP/(TP+FN),

(15)

FPR=FP/(FP+TN).

(16)

ROC曲线下面积(area under curve,简称AUC)[23]为ROC曲线与坐标轴包围的面积,描述分类器在特定阈值下识别样本的能力.AUC越接近1.0,方法的分类准确率越高.

4.3 参数设置

实验中,需要设置多重分形关联参数和深度CNN参数.参数设置如下:ω为0.5,训练集与测试集的比率为4∶1,epoch为300,batch_size为32,学习率为0.001.

4.4 实验结果及分析

为验证所提方法的优越性,将该文方法的分类准确率与文献[8-10]方法的分类准确率进行比较.表2给出了4种方法6种类型飞机的分类结果.

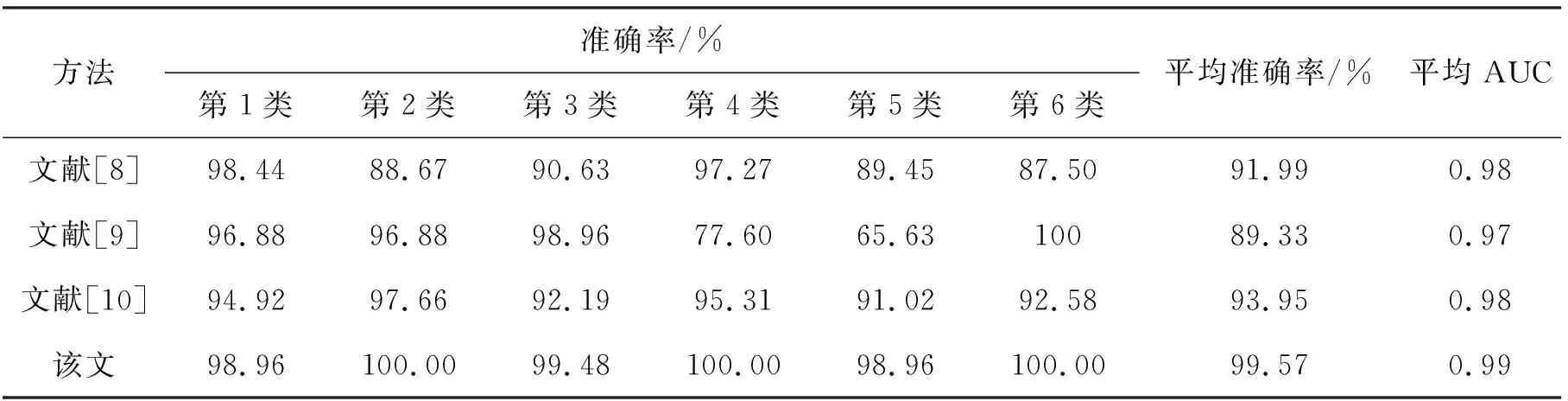
表2 4种方法6种类型飞机的分类结果

由表2可知:相对于文献[8-10]方法,该文方法的平均准确率最高,高达99.57%;相对于文献[8-10]方法,该文方法的AUC最高,高达0.99.因此,相对于其他3种方法,该文方法有更强的飞机分类性能.

5 结束语

该文将深度学习与多重分形关联特征相结合,对飞机进行分类识别.以多重分形关联谱投影图作为深度CNN的输入,利用深度CNN自适应学习多重分形关联谱中反映的不同类型飞机的特征.实验结果表明:相对于其他3种方法,该文方法有更强的飞机分类性能.该文研究也存在如下不足:①数据集有限;②网络结构没有改进;③多重分形关联谱是3维的,而该文使用的特征是2维的,没有充分挖掘多重分形关联谱的特征.后续研究拟克服这些不足,进一步提升分类准确率.