大型抛物柱面天线展开动力学分析与展开过程控制

2023-05-19 13:03陈金宝宋志成陈传志董家宇王治易

宇航学报 2023年4期

陈金宝，宋志成，陈传志，董家宇，王治易，张俞

(1. 南京航空航天大学航天学院，南京 210016；2. 深空星表探测机构技术工信部重点实验室，南京 210016；3. 上海宇航系统工程研究所，上海 201100)

0 引言

随着空间大型可展开天线的发展,星载天线的口径也越来越大[1-6],而大尺度引起的机构柔性对天线展开过程的影响也越来越明显[7],导致其存在显著的柔性体大变形与大位移耦合现象,难以得到展开驱动力与各展开参数间的解析模型,而明确机构运动参数与驱动力的映射关系是后续高效、高稳定控制的基础,为提高空间天线展开可靠性和部件受载安全性,必须全面识别天线展开过程中的动力学特性。为此,各学者针对天线展开过程中的动力学特性展开了较为深入的研究[8-9]。为精准描述可展天线柔性部件的弹性变形与大范围运动的耦合效应,绝对节点坐标法[10]备受青睐。杜雪林等[11]采用Gerstmayr提出的低阶柔性梁单元离散周边桁架式天线支撑机构的柔性杆件,并采用过渡单元模拟反射面索网的力学行为,建立了天线-张拉索的动力学模型。彭云等[12]基于几何精确梁建立了大型环形天线的动力学模型,并通过展开过程优化分析提升了天线展开过程平稳性。马小飞等[13]基于几何精确梁研究了大型椭圆环形桁架天线展开过程中柔性部件的力学行为。然而现有研究大都集中于周边式可展天线领域,针对抛物柱面天线这类具有大尺度、多闭环、强耦合特点的背壳式可展天线尚处于构型设计阶段[14-16],其展开过程动力学特性的研究并无相关权威文献可查。背壳式天线结构复杂,支撑桁架众多,运动副繁多且种类复杂,直接导致其动力学模型建立极为困难;同时,现有研究往往为了降低计算量采用不承受剪切变形与扭转变形的缩减梁单元[17],难以精确模拟抛物柱面天线这种背壳式桁架的受力特性,为了精确模拟其真实的力学行为,不得不用较为稠密的三维全参数梁单元来离散可展支撑桁架,最终组集的动力学方程规模往往相当庞大,导致计算耗时。面对大规模的非线性微分代数方程组,显示积分求解算法往往难以收敛,纵然是降低步长也难以实现长历时的仿真计算。因此,需采用隐式积分算法,这也导致在每个迭代步需求解弹性力雅可比矩阵,而求解弹性力雅可比将进一步增加动力学方程的求解难度和耗时量[18]。

现有大型空间天线的展开控制方面研究往往针对环形周边式等主动展开天线,而本文所研究的大型抛物柱面天线则采用被动形式展开,其展开驱动力由分布在刚性驱动组件上的圆柱弹簧提供,当释放外部约束后,可由收拢位形下展开至展开位形,若不控制弹簧势能的释放速率,滑块速度将随着展开过程逐渐加快并在锁定阶段具备非常大的速度,这必然导致各构件承受剧烈的冲击。

综上所述,针对大型抛物柱面可展天线,如何快速建立其精确的动力学模型,并建立高效的展开过程控制策略尚有待更进一步的研究。为此,为保障抛物柱面可展天线在轨稳定展开,确保各结构部件的力学性能,本文提出了针对大型抛物柱面天线的模块化动力学组装方法,并基于模块化思想进一步建立了逐块缩聚与递归求解的高维微分方程算法,通过非线性展开过程反馈控制策略降低了可展天线展开过程中驱动滑块的展开速度峰值,提高了抛物柱面天线在轨展开过程中的同步性。

1 抛物柱面可展天线支撑机构的基本梁单元

本文研究的抛物柱面可展天线在展开过程中,各刚性驱动件、刚性连接件是变形微小的粗短杆,可采用NCF(Natural coordinates formulation)模型[19]描述;对具有大变形、大转动的细长连杆,可采用ANCF(Absolute nodal coordinate formulation)模型描述。

1.1 基于NCF的刚性梁单元

抛物柱面可展支撑机构由驱动组件存储的弹性势能推动其展开,在展开过程中,可以忽略驱动组件的弹性变形,故将驱动组件中的各连接件视为刚体,进而可采用能得到常数质量矩阵的NCF单元。

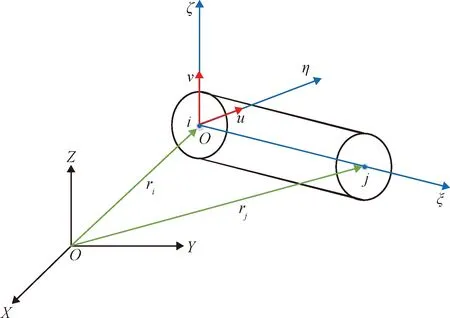
图1 NCF单元Fig.1 NCF element

如图1所示的空间NCF单元,采用全局坐标系中空间刚体上两端点的位置坐标[ri,rj]和两个相垂直的共面单位矢量坐标[u,v]作为广义坐标qe,即

(1)

则由(ri,rj,u,v)可构造NCF刚性梁单元的局部坐标系Oξηζ,记刚体上任意一点p在局部坐标系下的位置坐标为[Lc1,c2,c3],其中L为刚性梁的长度,点p在全局坐标系下的坐标列阵可表示为

rp=Cpqe

(2)

式中:Cp∈3×12,由于点p在局部坐标系中的位置是不变的,即c1,c2,c3为常数,因此矩阵Cp为常数矩阵。

1.2 基于ANCF的柔性全参数梁单元

抛物柱面天线此类背架式天线因其复杂的连接形式,同时存在着沿弧面方向的分力使可展支撑机构中的连接单元承受剪切力与扭转力,若采用ANCF缩减梁单元难以准确模拟抛物柱面可展机构中柔性梁因扭转与剪切效应对展开过程的影响[11],因此,本文采用能精确模拟柔性部件受力特性的ANCF全参数梁单元,如图2所示。

图2 ANCF全参数梁单元Fig.2 ANCF full-parameter beam element

相较于缩减梁单元,全参数梁引入了在梁截面内的位移梯度,从而梁端点ei包含12个节点坐标,并有

(3)

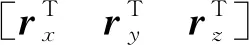
(4)

根据单元连续性可知,梁单元内任意点p的全局位置坐标rp是梁端点节点坐标的插值函数,用形函数表示为

rp=S(x,y,z)e=

(5)

式中:I∈3×3为单位矩阵;插值形函数的具体形式如下:

(6)

式中:L表示梁单元长度。

2 抛物柱面可展支撑机构动力学模型的模块化组装方法

本文研究的抛物柱面可展支撑桁架如图3所示,该机构由三类基本子环组成,分别是弧面子环(BUD)、柱面子环(MBUG)与辅助面子环(ABUG),C0为卫星机械臂与天线的连接点。需要指出的是,抛物柱面可展支撑机构辅助面在提高系统整体稳定性的同时还可以提供辅助驱动,促使天线展开。

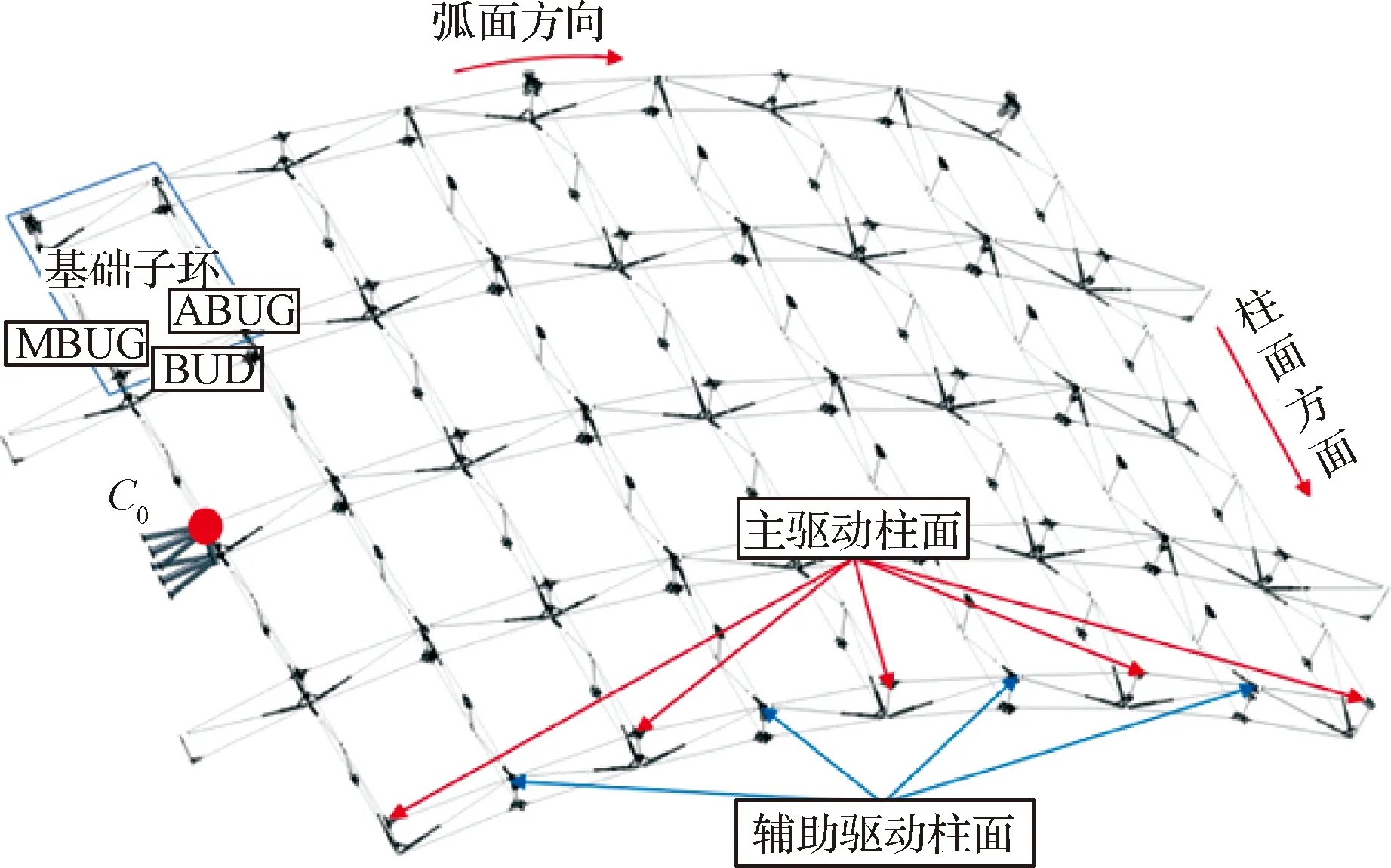
图3 抛物柱面可展支撑桁架Fig.3 Parabolic cylindrical deployable truss

其中,BUD,MBUG和ABUG三类子环的几何构型相同但几何尺寸不同。

图4 基本可展单元Fig.4 Configuration of BUD and MBUG

可展单元,如图4所示其展开驱动力由作用于滑块上的预压弹簧提供,推动滑块a在竖向连杆上移动,从而同步带动各子环展开,直到连杆de触碰限位点H,各杆件的运动随之停止,机构锁定,滑块展开到位。

该抛物柱面可展支撑机构动力学模型的建立过程是极为复杂的,其具体体现在建立大规模广义坐标之间的约束方程,以及约束方程雅可比矩阵的建立过程。抛物柱面天线是包含大量铰接约束、滑动约束与刚接约束的刚柔耦合多体系统,若逐一建立该系统的约束方程,将面临繁重的工作量。值得一提的是,往往此类背壳式大型天线系统,其整体构型可拆分为若干子模块,如抛物柱面天线可拆分为25个主驱动子模块与16个辅助驱动子模块,如图5所示。

图5 组装构型Fig.5 Assembly configuration

显然图5中的25个主驱动子模块均由BUD子环与MBUG子环组成,16个辅助驱动子模块均由ABUG子环组成,根据各子模块内子环的拼接方式,可归类为表1中的9种主驱动基本模块I0～I8和辅驱动基本模块I9;进一步分析I0～I8模块的几何组装构型可知,I1～I8这8类基本模块均可通过对基本模块I0执行切割剔除部分子环直接得到。

综合上述分析,大型抛物柱面可展支撑机构的动力学模型可拆分为25个主驱动动力学子模块和16个辅助驱动动力学子模块,且25个动力学子模块是由9种基本动力学模块组成,其中I1～I8是I0的子集,I0模块几何构型如图6所示,其由两个BUD与两个MBUG组成,I9模块均由ABUG子环组成。

图6 主驱动基本模块Fig.6 Basic module of main driver

由于三类子环均具有如图4所示相同的几何构型,可分别采用NCF梁划分刚性构件(梁截面为圆形截面),采用ANCF全参数梁划分柔性构件(梁截面为圆环形截面),在考虑计算精度并兼顾计算代价的同时,本文对子环中每根柔性构件用5个ANCF梁单元来划分。子环中各连接件的物理参数与几何参数如表2所示。

表2 物理与几何参数Table 2 Physical parameters and geometric parameters

BUD,MBUG与ABUG子环中的刚性驱动组件与刚性连接组件如图7所示,采用NCF单元将刚性驱动组件划分为7个梁单元{k′k,c′c,a′a, f′f,k′f′,ab,cd},将刚性连接组件划分为3个梁单元{g′g,h′h,gh},在建立动力学方程时,本文将滑块的质量与各连接节点的质量以质量点的形式平均附加到相邻的NCF梁的端点上。

图7 刚性组件Fig.7 Rigid components

对于刚性驱动组件,由于滑块在k′f′梁对应的矢量上滑动,与ab梁对应的矢量始终满足如下方程:

(7)

同时,θ需满足如下几何方程式:

(8)

上述方程组即可描述滑块的滑动约束,即

(9)

同时刚性组件与柔性梁组成的子环系统含有的刚接约束与旋转铰约束可分别表示为

(10)

式中:i,j表示铰接或者刚接的两个节点,ri,α(α=x,y,z)表示该点的局部坐标轴,ri,u表示铰接约束中的旋转轴矢量,对于绝对节点坐标法中的约束方程表达可具体参考文献[20]。需要指出的是,为了避免ANCF梁单元的泊松闭锁效应,本文在仿真计算时将泊松比设定为0,那么基于ANCF-NCF方法建立的I0模块动力学方程表示为

(11)

3 高维微分动力学方程组逐块缩聚与递归求解算法

抛物柱面天线系统约束方程通过拉格朗日乘子法引入到整体动力学方程中,从而建立描述多体系统动力学特性的指标-3(Index-3)微分-代数方程组(DAE),对于该微分-代数方程组的求解方法,目前常用的方法有Baumgarte方法、Bathe积分策略、Newmark方法、HHT-I3方法与Generalized-a方法等,田强等[21]全面对比了各类数值求解算法的优缺点,本文采用Newmark算法来求解上述微分代数方程组,Newmark算法通过差分直接将动力学方程离散为代数方程组:

(12)

其中,

(13)

式中:h为积分步长,Newmark算法可通过参数η,γ,来调整求解过程的计算精度与效率,往往为了使得Newmark算法稳定可取γ≥1/2,η≥(γ+1/2)2/4。本部分基于Newmark方法,以广义加速度与拉格朗日乘子为迭代未知变量,在第k个牛顿迭代过程中,均需求解如下代数方程组:

(14)

式中:

(15)

所以有

(16)

由于抛物柱面天线广义坐标数目与约束方程数目量级均非常高,导致微分代数方程(14)的维度非常高,而超大型矩阵的求逆过程是极为耗时甚至是无法求解的,为了求解上述微分方程组,本文在动力学方程模块化的思想上,进一步基于模块化提出逐块缩聚与递归的求解方法。

借鉴于静力缩聚思想,将抛物柱面可展支撑机构的广义坐标分模块划分为q={qj|j=1,2,…,41},qj为Hj模块中的广义坐标。Hj模块中的广义坐标数目为u,该模块内所包含的约束方程数目为s。此时,不包含Hj模块的广义坐标总数为v,不包含Hj模块的约束方程总数为t,从而,矩阵方程(14)表示为如下分块矩阵形式:

(17)

式中:

(18)

方程(17)中下标带b的矢量或矩阵属于被缩聚的模块Hb,下标带i的矢量或矩阵为待缩聚参数,将其重新组装为如下的分块形式:

(19)

式中:

(20)

(21)

将模块Hb中的未知变量缩聚:

xb=(Θbb)-1(Gb-Θbixi)

(22)

代回方程式(19),获得下一个待缩聚的矩阵方程:

Eixi=Pi

(23)

式中:

Ei=Θii-Θib(Θbb)-1Θbi,Pi=Gi-Θib(Θbb)-1Gb

(24)

重复步骤(17)～(22),逐一缩聚子模块H1～H40,然后再递归求解各未知变量,该逐块缩聚与递归求解步骤可由图8表示。

图中,df为收敛判断参数,d0=0.001为常数。显然,求解缩聚模块xb=(Θbb)-1(Gb-Θbixi)的微分方程要高效容易的多,将最终得到的加速度增量与拉格朗日乘子增量代回方程(16),便可实现大型柔性多体系统动力学微分方程组的求解。

图8 逐块缩聚与递归求解算法Fig.8 Module-by-module condensation and recursive solution algorithm

4 大型抛物柱面天线展开动力学分析

抛物柱面天线在完全收拢状态下,难以通过分布在刚性驱动组件上的圆柱弹簧使其展开,此时由分布在旋转铰关节上的扭簧提供驱动力使其展开到驱动位形,再由圆柱弹簧提供展开驱动力。待可展天线展开到驱动位形时,其驱动形式变换为由分布在刚性驱动组件上的圆柱弹簧组成,其中主驱动弹簧25个、辅助驱动弹簧20个,主驱动弹簧驱动力Qz及辅助驱动弹簧驱动力Qf与滑块行程之间的函数关系为

(25)

故此,抛物柱面可展天线动力学微分方程的初始边界条件包含天线初始构型及所受的广义外力,

(26)

式中:q0是可展天线驱动位形下各节点的广义坐标。根据图5可知,S表示滑块相对局部坐标原点o的距离,随着天线展开,那么S的值一直减小。在弹簧力开始作用时主驱动滑块相对o点的距离为277 mm,辅助驱动滑块相对o点的距离为276.6 mm,展开到位锁紧时各滑块相对o点的距离均为160 mm。根据图8所示的求解流程,可以求解得到抛物柱面可展天线在展开过程中各柱面中心主驱动滑块相对o点的位置轨迹。

图9给出了3、8、13、18、23号滑块的位置曲线,该五个滑块均为位于第一、第二、第三、第四与第五号柱面的中间滑块,可以很明显的看到,在展开到19 s之后,可展机构不同柱面呈现出较大的展开不一致性,由图9可知第一个柱面展开较快,第二个柱面展开较慢。

图9 不同柱面中心滑块位置轨迹Fig.9 Tracks of sliders on different cylinders

展开全过程中任意两滑块的最大位置差值如图10所示,其表征了可展机构展开过程的同步性,同步性越高,位置差值越小,反之越大。由图中所示结果可知,可展支撑机构在展开到19.5 s时位置差值显著增加,在20.6 s时达到68.41 mm的峰值,随后瞬速减弱,直到所有柱面均展开到位。

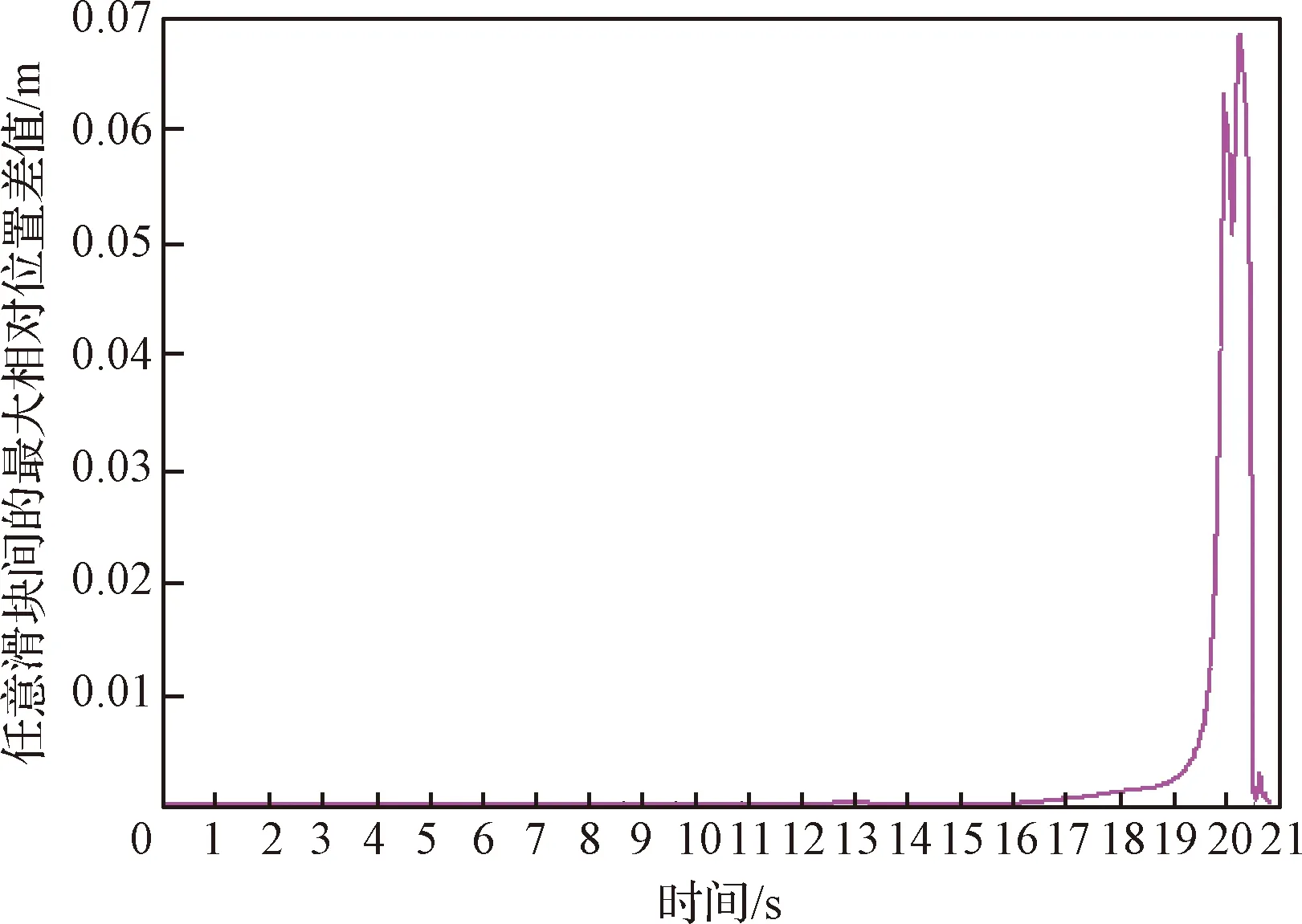
图10 任意两滑块的最大位置差值Fig.10 The maximum position difference between any two sliders

在滑块位置差值最大时天线支撑机构的第一个柱面已经展开到位,此时可展支撑机构的展开构型如图11所示。

图11 展开位置差值最大时可展支撑机构展开构型Fig.11 The deployed configuration of the deployable supporting structure when the position difference is maximum

从图11可以发现,第一个柱面基本展开到位,第二个柱面展开程度最低。由于各主驱动柱面滑块展开速度趋势一致,此处给出了抛物柱面可展天线支撑机构第三号主驱动柱面各滑块的速度曲线,如图12所示。

图12 滑块速度曲线Fig.12 Speed of the slider

在这里,滑块速度为负值表示展开状态,滑块速度为正值表示收拢状态。由滑块速度轨迹可知抛物柱面可展支撑机构在展开前19 s内速度增长非常缓慢,各柱面上的滑块速度均小于0.02 m/s,此时各滑块展开位置在0.25 m附近,即在可展支撑机构展开前19 s,滑块行程仅为0.027 m;在19.5 s之后各滑块速度出现飞速递增直至各可展支撑单元展开到位,滑块的最大速度峰值达到2.996 m/s,且在展开末期滑块速度变化剧烈,表明可展天线呈现出剧烈振动。综合上述分析可知该可展支撑机构的展开过程呈现出高度的非线性,展开末时滑块速度过快,在到位锁定时对可展支撑机构造成较大冲击,激发天线系统振动,影响整体卫星系统稳定性。因此,需制定合理的控制方法保障天线展开过程中的稳定性。

5 大型抛物柱面天线展开过程控制

5.1 基于被动展开的双边缓释方案设计

本文基于所研究的抛物柱面天线被动展开控制形式,制定了沿主驱动柱面方向的双边缓释方案对其展开过程进行控制,如图13所示。

图13 缓释驱动方案Fig.13 Drive strategy

缓释驱动方案为采用一条柔索贯穿柱面方向上的多个基本折展单元,由于摩擦力、铰链黏性阻尼等因素的存在,柔索每经过一个传动件,其上的张力就衰减一部分,影响天线的展开同步性。为了降低因摩擦、阻尼等因素引起的天线展开过程不一致,本文将缓释驱动装置设置在柱面方向上的两侧,通过由两侧向中心同步释放柔索,控制展开速度。但由于摩擦的影响,作用于各滑块上的力显然要比上述数值小,马小飞等[13]对此有相关研究,指出柔索驱动力以幂指的形式衰减,该衰减的驱动力定义如下:

Fi+1=cdFi

(27)

式中:cd为张力衰减系数,与滑轮摩擦系数相关。根据方程(27)可知,随着拉索经过的滑轮越多,摩擦引起的影响越大,缓释力衰减的越多。

为此,为保障同一柱面作用于各滑块上的缓释力大小接近,本文设定如图14所示的主驱动柱面滑块拉索走线模式。为进一步保证作用于各滑块上缓释力的均匀性,可通过滑轮摩擦系数选型使得张力衰减系数为预设值,本文各滑块张力衰减系数预设值为c1=0.9,c2=0.9,c3=0.17,那么该柱面各滑块最终所受的控制力为

(28)

图14 主驱动柱面滑块拉索走线方案Fig.14 Cable routing strategy of cylinder slider

5.2 基于滑块位置与速度反馈的控制器设计

对于第三节建立的动力学模型,在系统方程中引入缓释控制力,

(29)

-0.04 m/s≤si(i=1,2,…,25)≤-0.001m/s

(30)

基于上述分析,为实现天线展开过程中的稳定控制,本文制定如下形式的反馈控制力:

(31)

式中:up(s)与滑块位置有关,

up(s)=Qz(s)

(32)

(33)

根据反正切函数的性质可知,在滑块速度达到-0.04 m/s和0.02 m/s附近时,控制力将陡然增大或减小,实现对天线非线性展开过程的反馈控制。

在天线展开过程控制中,可展天线的初始构型与弹簧驱动力为初始输入,在每个迭代步求解动力学微分方程得到天线系统各节点的位置、速度及加速度参数,以主驱动滑块的位置与速度为参考获得缓释控制力,从而建立输出反馈控制闭环。基于滑块位置与速度的输出反馈控制框图如图15所示。

图15 输出反馈控制框图Fig.15 Output feedback control block diagram

5.3 抛物柱面天线展开过程分析

根据图14所示的天线展开过程控制方案,需布置10套缓释控制装置,每套缓释控制装置质量为3 kg,以质量点的形式附加到对应节点引入系统方程。双边缓释控制方案是通过两边的电机提供控制力,因抛物柱面展开机构具备对称性,为此两电机控制力大小设定为一致,同时因摩擦阻尼的影响,导致由图14所示的拉索走线方式施加在各滑块上的控制力大小保持固定比例,而无法根据各滑块速度进行反馈调节。在此,设定不同柱面上缓释电机的控制力大小根据该柱面上中心滑块(3号滑块)的速度来施加,缓释控制力大小通过方程(31)获得。

最终可展支撑机构在展开过程中各主驱动柱面中心滑块位置轨迹如图16所示,由双边缓释控制作用下五个柱面上中心滑块的轨迹曲线可知,可展天线支撑机构各主驱动柱面中心滑块的展开趋势一致,但因为控制力无法满足对每个滑块展开末期速度的精准控制及可展机构的弹性变形,各滑块展开到位时间有所不同,图17给出了4个辅助驱动柱面中心滑块的位置轨迹。