熔融液柱与冷却剂作用中液柱碎化预测

李爽岚,刘鹏飞,贺隆坤,匡 波

(上海交通大学 核科学与工程学院,上海 200240)

在轻水堆堆芯熔化的严重事故进程中,熔融燃料可能将压力容器下封头熔穿,掉入堆腔水池发生熔融物和冷却剂相互作用(FCI),甚至可能进一步发生蒸汽爆炸。熔融燃料液柱的碎化是FCI过程中的主要物理现象,决定了粗混合的状态。由于蒸汽爆炸的强度很大程度上取决于熔融物颗粒和蒸汽在熔融燃料与冷却水中的体积比,液柱碎化模型在核安全预测分析中相当重要[1-2]。但是液柱碎化机理复杂,影响因素众多,现有碎化模型预测结果与实验数据有较大差异。

近些年来,关于FCI行为预测模型的研究日益增多。Zhou等[1]采用VOF方法发展了多相流代码,模拟了水液柱射入熔池的水动力行为,并与实验数据进行了比较,验证了代码的有效性。Li等[2]在不考虑热传递和相变的情况下,发展了熔融液柱水力学碎化的数值模型,得到了计算碎裂长度和熔融物-冷却剂无量纲接触面积的经验关系式。一些学者考虑到了熔融物表面沸腾对FCI过程的影响。Yoon等[3]改进了原始的Epstein-Hauser模型[4],将熔滴表面到气液界面的辐射传热项加入到汽-液界面的热平衡公式中,计算结果表明该改进模型对膜态沸腾传热的预测精度较原始模型更高。Zhong等[5]构建非平衡多相流模型模拟了FCI爆炸阶段过程,为蒸汽爆炸压力上升提供了一种理论分析方法。Mahapatra等[6]基于有限体积离散法和SIMPLE压力修正算法,建立了膜态沸腾条件下三相(颗粒、液体和蒸汽)流动和热相互作用的传热分配模型。Li等[7]采用无网格移动粒子半隐式(MPS)方法在拉格朗日框架中模拟了有无初始汽膜的UO2熔滴的碎裂行为。现有研究更多聚焦在熔滴碎化预测,在FCI粗混合阶段的液柱水力学碎化行为预测方面,特别是考虑熔融液柱表面沸腾影响因素的研究还比较少。

本文采用实验验证和理论分析相结合的方法,通过高温熔融液柱碎化实验获得碎化过程关键实验现象和实验数据,然后基于液柱表面沸腾模型和熔融物剥离模型,构建液柱水力学碎化预测模型,对不同沸腾条件下的液柱碎化过程进行预测。完成实验数据与预测结果的验证分析后,将模型进一步推广到反应堆原型材料熔融液柱的碎化预测中。

1 液柱碎化实验

1.1 实验装置

本文涉及的熔融液柱碎化实验在TIMELCO装置中进行,实验装置工作原理如图1所示。实验装置的重要组成部分包括高温炉、释放管、反应容器、压力容器和测量系统等。红外测温仪通过测温通道测量坩埚外表面温度,二硼化锆复合陶瓷热电偶通过伸入高温炉内部接触坩埚外表面测量坩埚外表面温度。高温熔炉通过红外测温仪和二硼化锆复合陶瓷热电偶数值比较获得炉膛准确温度。反应容器水温和气温测量不确定度为0.42 ℃,红外测温仪工作误差为1.5%,二硼化锆复合陶瓷热电偶不确定度为4.6 ℃。详细实验装置和实验过程在前期文献[8-10]中已有介绍,本文不再展开。

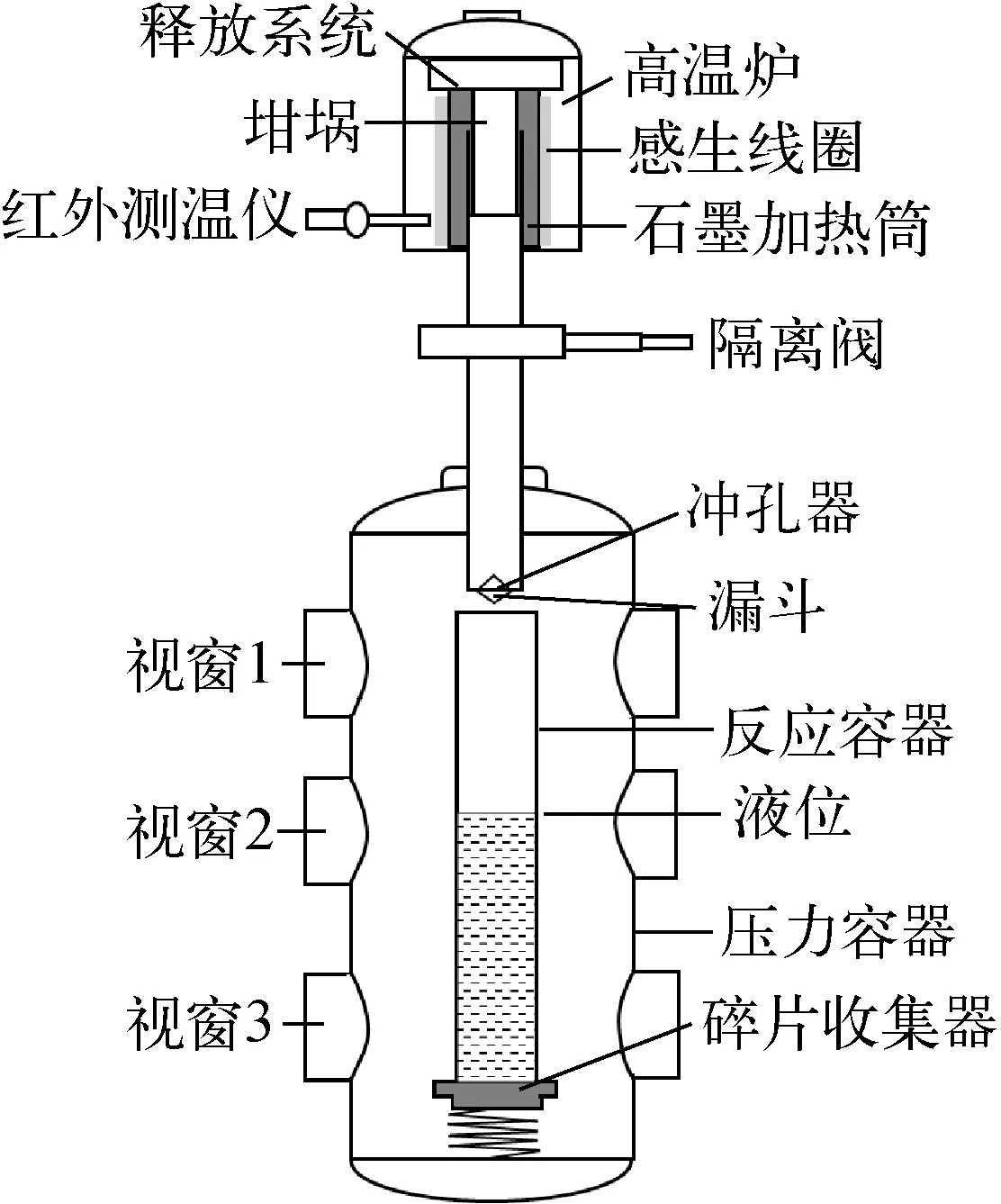
图1 TIMELCO实验装置示意图Fig.1 Schematic diagram of TIMELCO experimental apparatus

1.2 实验方法

实验通过改变水的过冷度和熔融物过热度来研究不同沸腾条件下液柱和冷却水的相互作用机理。熔融物材料选用锡和不锈钢两种金属材料。锡的熔点为232 ℃,容易获得更高的过热度,避免凝固带来的影响;不锈钢的熔点为1 427 ℃,能够更好研究实际反应堆中剧烈沸腾条件下的液柱碎化机理。液柱过热度和冷却水过冷度的选取主要参考KROTOS的实验工况[11]。熔融物质量均为3 kg,冷却剂为去离子水,液柱直径为25 mm。实验过程中整个系统处于封闭密封状态,通过高速摄像观察液柱落水后的碎化过程,并结合实验获取的碎裂长度和碎片中位直径来分析液柱碎化机理。液柱在碎裂长度以前是连续的,到达碎裂长度以后,以分散的颗粒状下落。碎裂长度直接反应了液柱入水后碎化的快慢,可通过高速摄像中观测到的液柱前端速度变化来确定。利用实验后底部碎片收集器中收集到的碎片尺寸分布结果确定碎片中位直径。

1.3 实验结果

锡液柱的碎化图像如图2所示。在70 ℃水温下,水的过冷度较低。液柱和冷却剂接触后,液柱表面被1层薄的稳定蒸汽膜包裹。随着液柱的下落,液柱侧面发生熔融物的剥离,前端发生的碎化相对较少。

图2 熔融锡液柱碎化过程Fig.2 Fragmentation process of molten tin jet

熔融不锈钢液柱碎化过程如图3所示,不锈钢液柱落入冷却水后,表面会被1层蒸汽膜覆盖,与锡工况相比,蒸汽膜更厚。蒸汽以较大速度向上流动,处于稳定膜态沸腾状态。在接近反应容器底部,不锈钢液柱已经因为水力作用碎化成了颗粒,但颗粒表面仍处于膜态沸腾状态。两种材料的液柱碎化实验得到的碎片中位直径和碎裂长度列于表1。锡和不锈钢碎化实验得到的碎片尺寸分布如图4所示。

图3 熔融不锈钢液柱碎化过程Fig.3 Fragmentation process of molten stainless steel jet

2 数值模型

由于实验的液柱直径较小(<0.1 m[12]),水滴卷入蒸汽膜引起的冷却水去除率较小,而且液柱表面波动和蒸汽膜厚度处于同一个数量级,熔滴降低最大汽速,从而增加蒸汽膜厚度[13]的作用有限。另外,实验观察到液柱长度较长,碎化主要发生在液柱侧面。为简便起见,本文不考虑夹带和液柱前端发生瑞利-泰勒不稳定性(R-T)不稳定性碎化的影响。对液柱碎化行为的预测建立在两相边界层理论、开尔文-亥姆霍兹不稳定性(K-H)不稳定性理论的基础上,采用液柱表面膜态沸腾模型和液柱表面不稳定波生长模型对液柱碎化过程进行描述,并在Matlab环境中开发了液柱碎化计算软件。本文假设模型与时间无关,碎裂长度固定,液柱直径和液柱入水速度保持不变。

表1 熔融液柱碎化实验结果Table 1 Experimental result of molten jet fragmentation

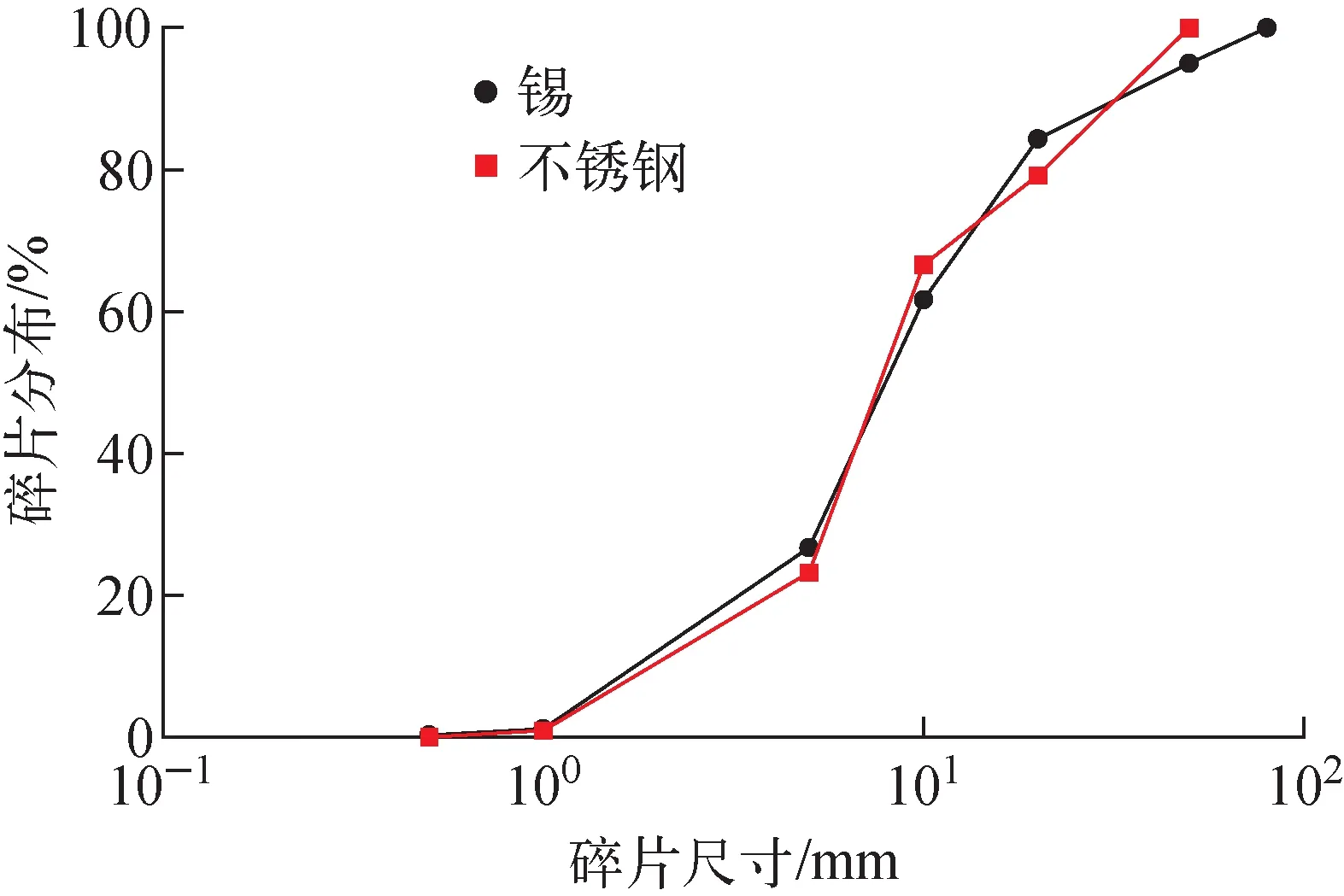
图4 不同材料反应后的碎片尺寸分布Fig.4 Debris size distribution under different jet materials

2.1 层流态蒸汽膜态沸腾模型

当液柱温度高于冷却水最小膜态沸腾温度,但并未高出很多时,液柱和冷却水之间存在1层厚度很薄、速度很慢的蒸汽膜。参考Nishio等[14]提出的蒸汽膜单元模型,提出层流态蒸汽膜态沸腾模型。层流态蒸汽膜态沸腾图如图5所示,忽略液柱曲率的影响,由于气液界面受K-H不稳定性的影响,蒸汽膜由一系列的蒸汽膜单元组成。单元长度为K-H波最不稳定波波长,蒸汽传热特性在单元长度内保持不变。由于蒸汽膜单元的长度较短,蒸汽膜无法充分发展成湍流,可以认为蒸汽流动处于层流状态。

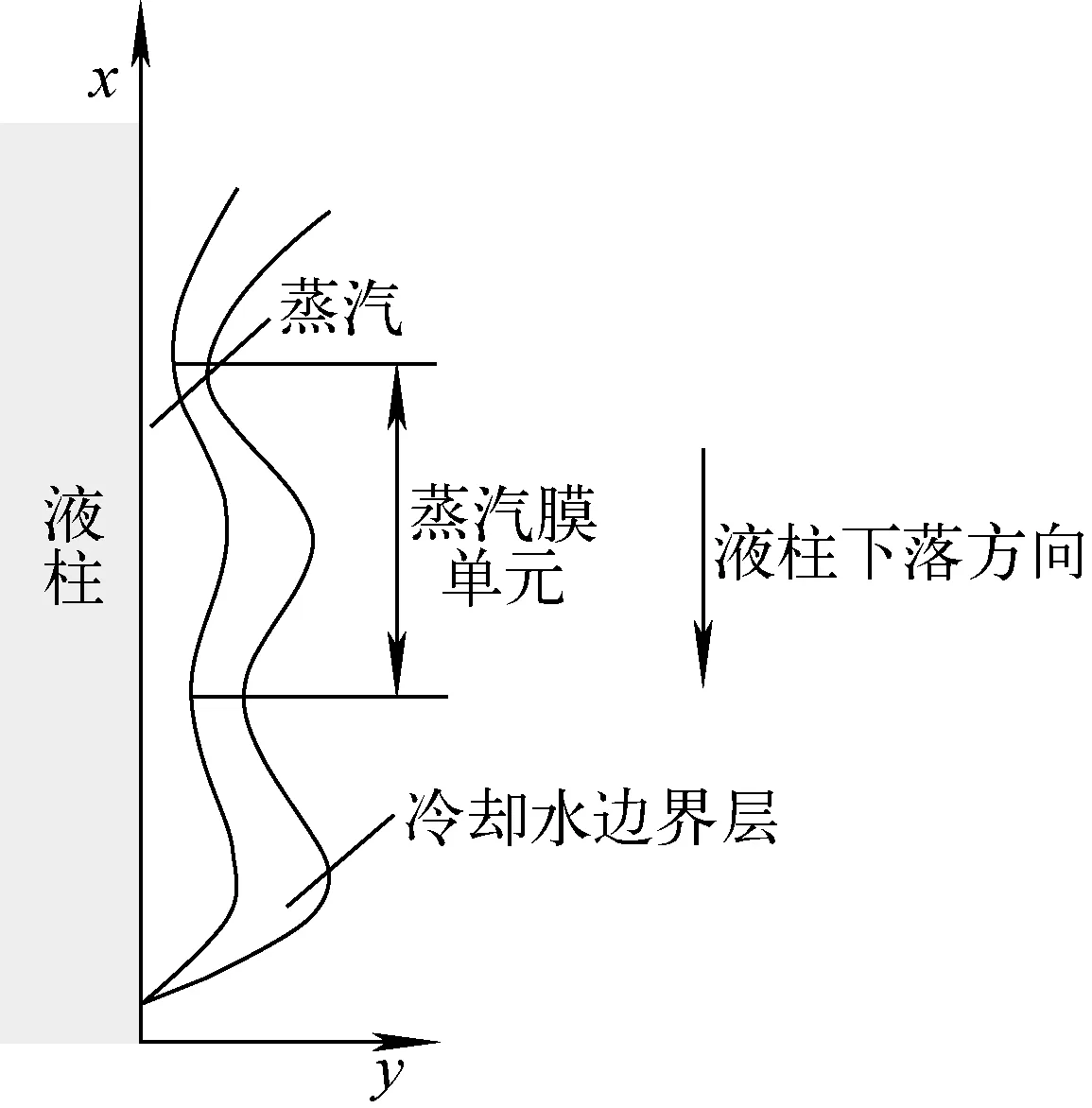
图5 层流态蒸汽膜态沸腾图Fig.5 Schematic diagram of vapor film boiling model under laminar flow condition

蒸汽膜内蒸汽动量方程:

(1)

蒸汽膜内能量方程:

hrad(TW-Tsat)

(2)

冷却水边界层能量方程:

(3)

最不稳定波波数及波长:

(4)

(5)

式中:下标v、c、W、sat、0分别表示蒸汽、冷却水、液柱壁、饱和态和冷却水主体;μ、ρ、g、k、hrad、Δhcv、cp分别为动力黏度、密度、重力加速度、导热系数、等效辐射传热系数、汽化潜热和比定压热容;U、u为截面平均速度和局部速度;δ、T为蒸汽膜和冷却水边界层的厚度、温度;y为径向坐标,x为轴向坐标;σ为张力;kp、λ为波数和波长。通过数值求解,可求得蒸汽膜厚度和蒸汽速度在蒸汽膜单元内的分布。以上所有物理量均采用标准国际单位制。

2.2 湍流态蒸汽膜态沸腾模型

当液柱温度远高于最小膜态沸腾温度时,液柱表面形成的蒸汽膜将液柱和冷却水分隔开来。冷却水边界层接收从液柱辐射和气相导热来的热量,不断沸腾蒸发,以蒸汽的形式向外溢出。此时,蒸汽膜不再由一系列的蒸汽膜单元组成,膜厚沿相对液柱下落的方向不断增加。如果液柱足够长,蒸汽膜的厚度足够大,那么蒸汽膜内将出现湍流。湍流态蒸汽膜态沸腾图如图6所示,蒸汽膜前缘初始位置由于蒸汽膜较薄,蒸汽速度较低,还处于层流状态,仍适用于前面的层流态模型。沿冷却水相对液柱表面流动的方向经过一段距离后,层流发展成湍流,但湍流靠近液柱壁面的位置仍存在1层层流。根据Han等[12]和Bürger等[15]提出的液柱表面膜态沸腾模型,层流在当地雷诺数Re达到100时开始发展成湍流。

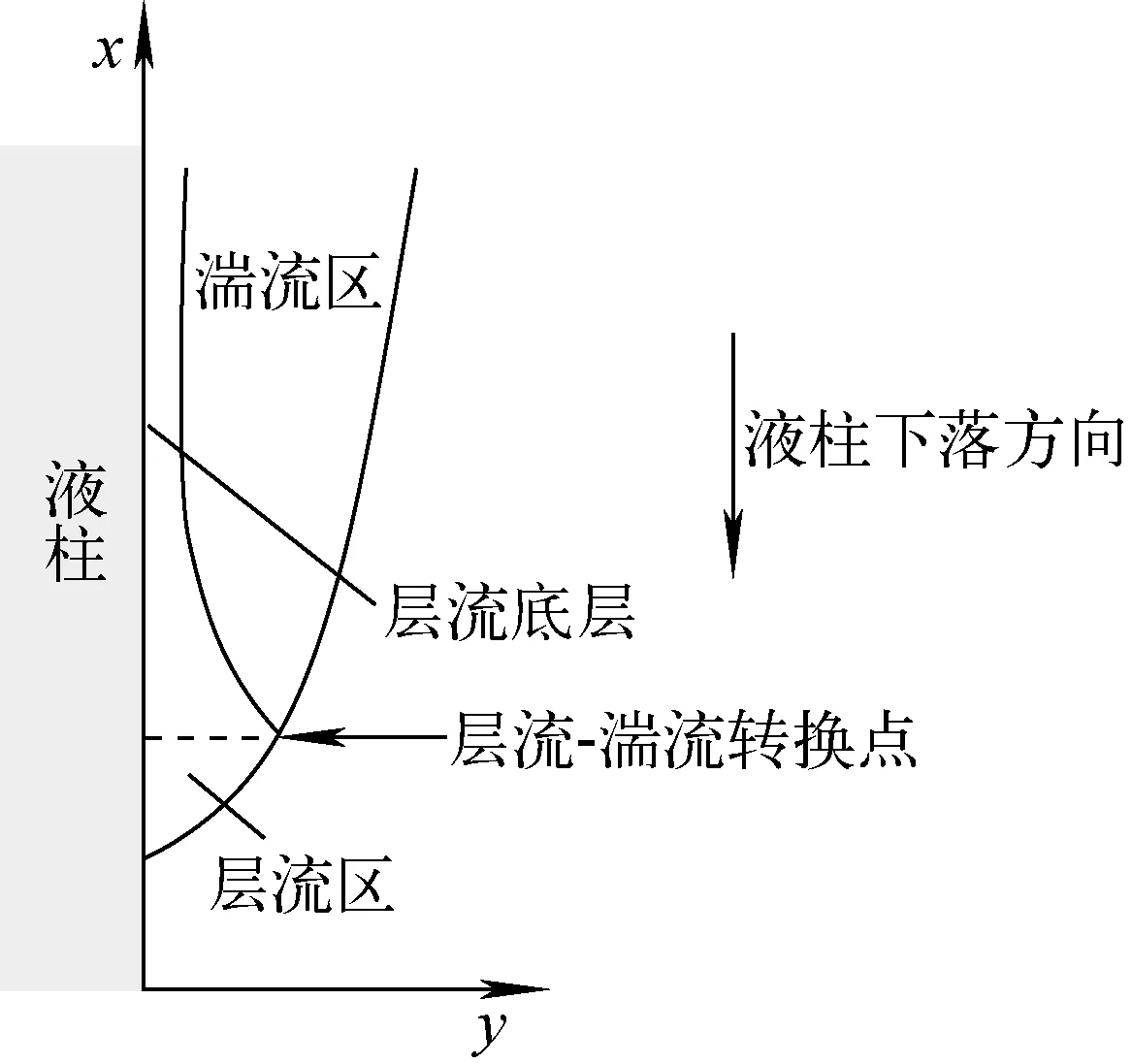
图6 湍流态蒸汽膜态沸腾图Fig.6 Schematic diagram of vapor film boiling model under turbulent flow condition

由于层流的厚度远小于湍流的厚度,忽略底层层流蒸汽过热从壁面吸收的热量,蒸汽膜内能量方程如下:

(6)

冷却水吸热汽化的质量速率为:

(7)

蒸汽温度变化只发生在底层层流,湍流温度保持不变,壁面通过热传导传递给气液界面的热量为:

(8)

壁面通过热辐射传递给气液界面的热量为:

(9)

气液界面传递给冷却水的热量为:

(10)

冷却水热边界层厚度为:

(11)

蒸汽膜内动量方程为:

(12)

底层层流与湍流的分界面为:

(13)

式中:下标t、l、j、c表示湍流、层流、液柱、冷却水;Δhcv为汽化潜热;c为气液界面辐射吸收率;ε为发射率;kB为史蒂芬-玻尔兹曼常数;α为热扩散系数;z为液柱下落距离;τ为蒸汽受到的摩擦阻力;含多字母的下标含义为各字母的含义组合,如vt表示蒸汽湍流。湍流态蒸汽膜态沸腾模型的蒸汽膜厚度和蒸汽速度的初始值由前文的层流模型确定。通过联立式(6)～(13),求得蒸汽膜厚度和蒸汽速度在液柱轴向的分布。

2.3 熔融物剥离模型

通过高速摄像,可观察到熔融物和蒸汽一起波动生长。于是在Epstein和Fauske[16]的工作基础上,考虑蒸汽膜厚度为一定值的情形,建立液柱-蒸汽和蒸汽-冷却水的双界面K-H不稳定性波模型,两者对应的波数和生长常数相同。然后根据蒸汽膜态沸腾模型的守恒关系式求取蒸汽膜厚度和蒸汽速度在液柱轴向的分布,计算两者在碎裂长度内的积分平均值,作为不稳定波模型的蒸汽膜厚度和速度输入值。剥离模型存在非零解的条件:

{ρv(n-kuv)2+[ρc(n-kuc)2-σck3]tanh(kδv)}·

ρv(n-kuv)2[ρc(n-kuc)2-σck3]=0

(14)

式中,k、n为波数和波生长常数。容易看出,当蒸汽膜的厚度和速度为确定值时,该方程为关于波生长常数的四次方程。当波数k的取值使n的虚部最大时,不稳定波的幅度增长得最快,此时对应的波为最不稳定波,熔融物最易脱离液柱主体。

最不稳定波波幅长到一定高度时,波峰发生断裂,熔融物从液柱表面脱离,成为熔滴。熔滴直径d即为波峰断裂部分的长度,其与最不稳定波波数关系为:

(15)

式中,Ofr、Nfr和Mfr分别为波断裂时,断裂长度与波幅、波幅与波长、断裂长度与波长之比。

熔滴生长所需时间为:

(16)

液柱表面熔滴剥离速率为:

(17)

碎裂长度表达式为:

(18)

式中:τ1、τ为单个熔滴生长所需时间和从液柱主体剥离所需总时间;np、ηp和Vp为最不稳定波生长常数、波幅和生长速率;Ffr为熔滴生长所需时间与脱离液柱的总时间之比;D为液柱直径。

3 碎化过程的数值预测

3.1 锡液柱碎化预测

最不稳定波波长随蒸汽膜发展的变化如图7所示,当蒸汽膜的发展长度与预测的最不稳定波长相等时,对应的长度即为蒸汽膜单元长度。随着蒸汽膜发展长度的增加,最不稳定波波长急剧减小,趋于一个定值,表示这是一个稳定解,意味着蒸汽膜具有稳定性,不会因为受到扰动而发生坍塌。计算结果与高速摄影观察到的图像吻合。

图7 最不稳定波波长随蒸汽膜发展的变化Fig.7 Predicted length of fast interfacial vapor-liquid wave as function of vapor film development length

锡液柱落入70 ℃冷却剂后,蒸汽厚度、速度在蒸汽单元内的分布如图8所示。可看出,蒸汽膜最大膜厚0.3 mm,速度最高4.78 m/s,此时雷诺数最高只有15.2,蒸汽膜处于层流状态。通过层流态蒸汽膜沸腾模型和熔融物剥离模型的数值计算,液柱表面K-H不稳定波生长常数n随波数k的变化如图9所示。当液柱表面K-H不稳定波的波数取100时,生长常数取最大值12.3,此时为最不稳定波。根据文献[13]和文献[16],选取Mfr=0.15、Ofr=1、Ffr=0.8代入模型计算,得到的碎裂长度和碎裂中位直径列于表2。表2中相对误差=(预测值-实验值)/实验值×100%。将该模型计算的结果与实验结果进行对比,得到的碎裂中位直径与实验值的一致性较好,但碎裂长度的预测值偏小。将Ffr修正为0.5后,碎裂长度预测值与实验值符合得更好,相关原因在下文叙述。

图8 锡液柱1个蒸汽单元内的蒸汽膜厚度和蒸汽速度Fig.8 Distributions of vapor film thickness and vapor velocity in a vapor film unit along tin jet surface

图9 锡液柱表面不稳定波生长常数随波数的变化Fig.9 Growth constant versus wave number for tin jet

表2 锡液柱碎片中位直径与碎裂长度实验值和预测值比较Table 2 Comparison of experimental and predictive values of debris median size and jet breakup length for tin

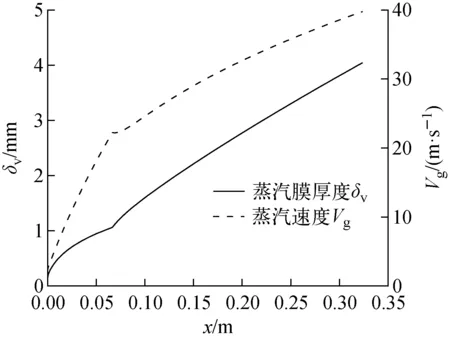
图10 不锈钢液柱表面蒸汽速度和蒸汽膜厚度沿高度方向变化Fig.10 Distribution of vapor velocity and vapor film thickness along stainless steel jet

3.2 不锈钢液柱碎化预测

60 ℃冷却水条件下,1 800 ℃不锈钢液柱以4.3 m/s速度入水以后,蒸汽膜厚度、速度分布如图10所示。图中转折点对应层流-湍流的过渡点。蒸汽膜平均厚度2.7 mm,速度平均值为31.9 m/s。液柱表面K-H不稳定波生长常数随波数的变化如图11所示。当液柱表面K-H不稳定波的波数取120时,生长常数取最大值26.5,此时为最不稳定波。碎片中位直径与碎裂长度的预测值与实验值比较列于表3。容易看出模型预测的碎片中位直径和碎裂长度与实验值比较一致。

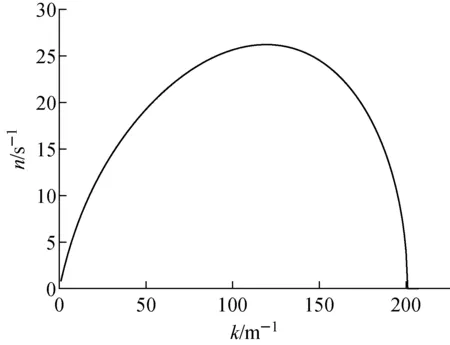
图11 不锈钢液柱表面不稳定波生长常数随波数的变化Fig.11 Growth constant versus wave number for stainless steel jet

表3 不锈钢液柱碎片中位直径与碎裂长度实验值和预测值比较Table 3 Comparison of experimental and predictive values of debris median size and jet breakup length for stainless steel

值得注意的是,此处Ffr取0.8时,碎裂长度和碎裂中位直径的预测值均与实验值符合得很好。为探究原因,对式(14)进行极限分析。当蒸汽膜厚度δv趋近于0时,tanh(kδr)→0,对应无沸腾或低沸腾工况。

此时式(14)的形式转换成:

ρj(n-kuj)2+ρc(n-kuc)2-(σj+σc)k3=0

(19)

最不稳定波数:

(20)

生长常数n的虚部取最大值:

(21)

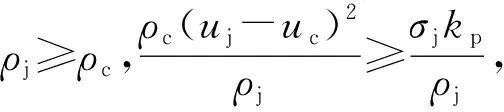
(22)

(23)

关于液滴稳定的临界韦伯数We为:

(24)

经典的低温情况下Epstein和Fauske半经验关系式为:

(25)

式中:下标rel表示相对值;E0为夹带系数。显然式(22)和式(24)形式相同,式(23)和式(25)形式相同。临界韦伯数取18[17-18]。当E0取0.1[16]、Ofr取1时,则Ffr取0.008 33。从低温无沸腾工况,到层流态沸腾工况,再到湍流态沸腾工况,Ffr取值不断增加。结合高速摄影观察到的实验现象和模型计算结果,不锈钢液柱入水后的沸腾程度较锡液柱更加剧烈。因此。沸腾更剧烈,气泡扰动更大,越有利于液柱的碎化。

3.3 原型材料液柱碎化预测

熔化的堆芯材料混合物,通常由(U,Zr)O2+Zr+Fe+B4C+裂变产物组成[19]。为了验证液柱碎化模型对反应堆原型材料液柱碎化预测的适用性,进一步开展了典型原型材料FCI实验液柱碎化预测分析。原型材料FCI实验中,熔融液柱温度较高(约3 000 K),液柱表面沸腾与上文中不锈钢液柱碎化实验类似,采用不锈钢工况的碎化模型对原型材料碎化进行预测分析。本文分别以公斤级的KROTOS实验和百公斤级大型FCI实验FARO实验为例进行熔融液柱碎化预测和对比分析。

KROTOS实验装置设计和实验条件与本文的TIMELCO装置较为相似。以KROTOS实验的NO.32工况[11]为例,具体实验条件为:熔融物成份为81.2%UO2+18.8%ZrO2,熔融物入水速度为4.2 m/s,液柱直径为30 mm,液柱温度为3 063 K,实验压力为0.1 MPa。碎片中位直径与碎裂长度的预测值和实验值对比列于表4。NO.32工况下的碎片中位直径预测值与实验值较为一致。由于KROTOS实验中采用反应容器侧壁的热电偶温度响应来判断液柱插入深度,无法获得准确的碎裂长度实验值,不能直接比较碎裂长度的预测值和实验值。实验结果显示,液柱插入长度大于0.15 m,结合模拟材料锡和不锈钢液柱的碎裂长度实验值,原型材料碎裂长度的模型预测值比较吻合实验值。

FARO实验选用了L-06[20]工况,具体实验条件为:液柱成分为80%UO2+20%ZrO2,液柱入水速度为6 m/s,液柱直径为100 mm,熔融物温度为2 923 K,实验压力为5 MPa。同样采用不锈钢碎化模型进行液柱碎化预测,模型计算得到的碎片中位直径与碎裂长度预测值分别为4.76 mm和0.73 m。预测值与实验值比较如表4所列。从表4可看出:L-06工况的碎片中位直径预测值和实验值一致性较好。受测量条件限制,FARO实验中也未能给出碎裂长度准确值,但从实验给出估计值来看,模型预测值与实验值也较为一致。

表4 原型材料液柱碎片中位直径与碎裂长度实验值和预测值比较Table 4 Comparison of experimental and predictive values of debris median size and jet breakup length for corium

4 结论

本研究采用实验和理论相结合的方法,构建了FCI过程粗混合阶段的熔融液柱水力学碎化模型,并完成了基于模型的液柱碎化预测值和实验值对比分析。通过分析,得到如下结论:

1) 通过实验可视化观察并结合模型研究,液柱表面的沸腾剧烈程度,影响蒸汽的流动状态和熔滴从液柱主体剥离的速率,进而影响液柱碎化的整个过程;

2) 对熔融锡和不锈钢液柱碎化进行预测时,碎化模型预测值与实验值符合得较好;

3) 将模型推广到典型反应堆原型材料FCI实验中的液柱碎化行为预测时,碎化预测结果与实验值也较为吻合。

本文提出的熔融液柱水力学碎化模型结果经过与实验数据对比分析后,初步验证了模型的适用性。但由于高温环境下液柱碎化实验难度大、观测困难,可用于模型验证的实验数据稀少,后续可进一步开展相关实验及模型完善研究,特别是应重点关注关键参数对液柱不稳定波断裂机制的影响。