含绕丝棒束内横向流动的可视化实验与数值模拟研究

孙牧川,王 汉,陆道纲

(华北电力大学 核科学与工程学院,北京 102206)

钠冷快堆与超临界水冷堆等第4代先进核能系统采用螺旋绕丝作为燃料组件的定位装置,绕丝一方面可实现燃料棒的准确定位,另一方面引导冷却剂在不同子通道间扫掠,发生周期性的横向流动与交混,从而强化与包壳的对流换热,有效降低包壳与燃料芯块的温度。因此,研究绕丝作用下棒束内冷却剂的横向流动特征对燃料组件的热工水力设计和运行安全具有重要意义。

近年来,国内外研究人员针对压水堆定位格架下游流场的实验测量[1-5]较为充分,而对螺旋绕丝诱发的棒束间横向流动研究非常有限。Nguyen等[6]及Goth等[7]采用粒子图像测速仪(PIV)测量了含绕丝61棒束内对伞花烃的速度分布,发现六边形壁面和绕丝改变了横向流动的对称分布规律,大尺度的非稳态结构与绕丝碰撞,破碎成细小的湍流涡。Zhang等[8]对含绕丝7棒束内碘化钠的流动特性进行了实验测量,结果表明,中心子通道的流速高于边缘子通道,涡流多出现在绕丝背风面。Wang等[9]对含绕丝单棒方环形通道内水的横向流动特性进行了PIV测量,获得了横截面的流线、平均流速、雷诺应力、湍动能等物理量随雷诺数及绕丝节距的变化特征。范大军[10]基于多种匹配折射率(MIR)方案对比,对19棒束内碘化钠的轴向速度分布进行了实验测量,并与数值模拟结果进行了对比。在数值模拟方面,Fischer等[11]采用大涡模拟对7棒束燃料组件内部流场进行了计算,研究表明,大涡模拟与雷诺时均模拟结果吻合较好,横向流速分布接近正弦函数。Gajapathy等[12]对带绕丝7棒束燃料组件的数值计算发现,螺旋绕丝在组件内引起了二次旋流,促进了冷却剂的横向交混,使其温度更加均匀。Liu等[13]对含绕丝19棒束内流动特性进行了三维计算分析,评估了不同形状绕丝的有效性,结果表明,圆形绕丝的摩擦阻力损失小于梯形绕丝,但梯形绕丝组件内的温度更加均匀。范旭凯等[14]对CiADS次临界反应堆燃料组件进行了数值模拟,发现7棒束与19棒束燃料组件的流场与温度场分布特性有相似性,横流分布在横向与轴向有明显周期性。

综上可知,大部分实验研究侧重于分析棒束内的轴向速度分布特性,且小尺寸棒束限制了PIV流场的空间分辨率。本文采用PIV与MIR方法对大尺寸含绕丝棒束内流体的横向流动特征进行高分辨率可视化实验测量与数值模拟分析。

1 实验装置

1.1 实验回路

实验回路如图1所示。实验回路由水箱、过滤器、离心泵、阀门、流量计和实验段组成。水箱中的去离子水加入示踪粒子后由离心泵送至实验段,流体流经实验段后返回水箱。实验段的流量与离心泵转速呈正比,可由变频器精确调节。回路中的泵、阀门和管道由不锈钢制成,水箱由亚克力板制成。

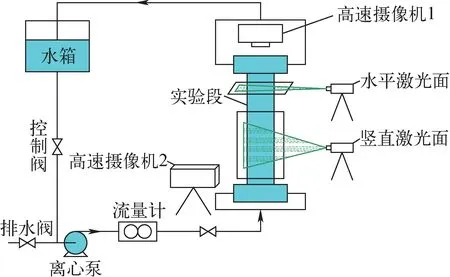
图1 实验回路Fig.1 Experimental loop

1.2 实验段

图2为实验段结构,7根亚克力管插入正六边形腔体中,形成含绕丝7棒束,水在棒束内垂直向上流动。亚克力管的直径为30 mm、壁厚为0.5 mm,相邻棒的中心距为35 mm,正六边形腔体内壁的边长为58.09 mm。室温下,氟化乙烯丙烯共聚物(FEP)的折射率(1.338)与水的折射率(1.333)非常接近,可减弱激光在绕丝与流体交界面上的散射、减小粒子的位移误差。因此,选择FEP作为绕丝材料。绕丝直径为5 mm、壁厚为0.3 mm、节距为500 mm。沿流体流动方向,绕丝沿棒逆时针旋转。实验段当量直径为13.17 mm、长度为1 560 mm。水从底部管道进入实验段,然后沿棒束和绕丝垂直向上(z方向)流动,最后从顶部腔室离开。实验雷诺数为3 000、6 000、9 000,对应的平均轴向速度分别为0.2、0.4、0.6 m/s。

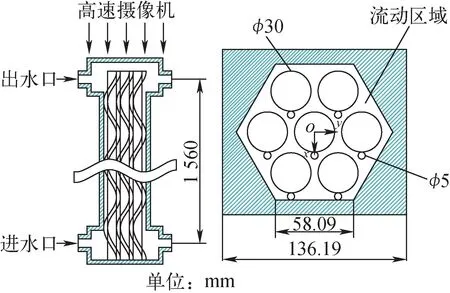
图2 含绕丝棒束实验段结构Fig.2 Structure of wire-wrapped bundle test section

1.3 PIV系统设置

可视化测量系统由二极管泵浦连续激光器、光学透镜组、高速摄像机、示踪粒子及图像处理软件组成。PIV片光的厚度为2 mm,激光器的最大功率为8 W,能量连续可调。采用Fastec TS3高速摄像机进行流场拍摄,分辨率为1 280×1 024像素,配备有尼康可调焦距镜头。示踪粒子采用颗粒直径为10～14 μm的空心玻璃微珠,其密度为1.04 g/cm3,具有良好的跟随性。在横截面流场测量中,激光平面水平穿过棒束横截面,高速摄像机1从棒束顶部垂直向下拍摄流场(图1)。根据雷诺数的不同设置拍摄帧数,如表1所列。为获得整个实验段横截面的完整图像,将棒束横截面划分为18个特征区域,包含内部子通道、边壁子通道和角子通道等3类子通道,如图3所示(图中数字为特征区域对应的编号)。在轴向截面流场测量中,激光平面竖直穿过第1层棒与壁面的间隙,高速摄像机2从正面拍摄流场(图1)。

表1 不同雷诺数下的摄像机参数Table 1 Settings of high-speed camera under various Reynolds numbers

图3 棒束横截面特征区域划分Fig.3 Partition of bundle cross-section

1.4 实验图像后处理

图像后处理软件为基于Matlab的开源程序PIVLab[15]。采用离散傅里叶变换算法对原始粒子进行计算,可显著降低由速度梯度、图像对粒子损失和高速运动模糊引起的测量误差。两次计算对应的判读区大小分别为64×32像素及32×16像素,重叠窗口50%。横截面每个特征区域分别拍摄1 000张瞬时速度图像进行计算,采用预先拍摄好的标定图像对图像进行标定,获得图像中的像素与粒子实际位移之间的换算系数,进而得到粒子的瞬时速度。后处理采用3σ法则对速度矢量进行筛选,去掉无效的速度矢量,并插入缺失数据。最后将处理后的1 000组瞬时速度进行总体平均,得到平均速度矢量。

1.5 误差分析

PIV测量的速度可由下式[16]计算:

(1)

式中:α为校准因子,是粒子在图像中的位移(像素)与实际位移(mm)之间的转换系数;Δx为粒子位移;Δt为相邻两帧图像的时间间隔;δU为粒子滞后等引入的误差。根据误差传递原理,速度矢量的合成不确定度为:

(2)

式(2)中,校准误差Uα主要来源于标记刻度的端点像素误差和透镜引起的标定图像畸变,约为0.5%。UΔx为粒子位移误差,与将粒子图像转换为速度矢量的算法有关,对于离散傅里叶变换算法,这一误差通常小于2%。UΔt为由激光引起的曝光时间误差,本实验采用连续激光拍摄,这一误差可忽略。UδU为实验系统中的测量误差,由3部分组成:1) 粒子在流场中的滞后性,本实验计算得到斯托克斯数St≈1.61×10-3,远低于滞后判定标准(St=0.1),表明粒子滞后引起的测量误差可忽略;2) out-of-plane测量误差[17],由于粒子在垂直激光平面方向的最大位移小于片光厚度(2 mm)的30%,可忽略平面粒子丢失造成的误差;3) 横截面流场测量中的视角误差,高速摄像机布置在远离测量平面的区域,视角误差不超过1%。Un为由样本数量引起的误差,综合考虑实验准确性和成本,每个特征区域拍摄1 000张图像,样本误差约为3.25%。基于上述不确定度分析,平均速度的合成不确定度为3.98%。

2 实验结果分析

2.1 横向流动特征

对PIV测量得到的1 000组瞬时速度矢量进行平均可得横截面平均速度,然后将18个特征区域的平均速度矢量进行拼合,得到如图4所示的横截面平均速度分布。图4工况的雷诺数为6 000,对应的轴向平均速度为0.4 m/s。从整个横截面来看,沿六边形腔体的内壁,流体的横向流动为顺时针方向。图4中靠近腔体上壁面的流体横向流速较大,最大横向流速约为0.14 m/s。在沿内壁顺时针流动的过程中,由于流体与内壁之间的相互作用以及绕丝对横流的阻碍作用,横向流速逐渐降低,经过底部与壁面近似接触的两根绕丝后,在图4中横截面左下角达到最低。同时从图4还可看出,在横截面上形成了几个局部涡流,这些涡流主要分为2种:第1种是由于流体与绕丝的作用而在棒束内部形成的湍流涡,这类涡主要出现在绕丝的迎风面,且旋转方向与横截面流动方向相反;第2种是由于棒束外围顺时针横流与棒碰撞,部分流体向棒束内部转向90°,从而产生一个顺时针旋向的大尺度涡流。

2.2 雷诺数对横向流速的影响

本文选取内部子通道和边壁子通道两个特征区域,分析雷诺数对速度分布的影响,两个特征区域对应的编号分别为图3中的6和10。雷诺数为3 000、6 000、9 000,对应的主流平均速度为0.2、0.4、0.6 m/s。

1) 内部子通道

2) 边壁子通道

与内部子通道处理方法相似,在边壁子通道定义一条特征线,该线从六边形内壁面开始,到4、5两根棒之间的中点结束,特征线长度为20 mm。图6为两个方向的速度分量沿10号边壁子通道特征线的变化规律。由图6a可看出,速度分量U从0 m/s开始增加,到特征线L=9 mm时出现峰值,然后缓慢下降直至保持稳定。这一变化趋势符合理论预期,即由于腔体壁面对流体质点的黏附作用,速度分量为0 m/s;离开壁面越远,流体的黏性作用越弱,速度分量逐渐增大。需要注意的是,在特征线的前半部分,雷诺数9 000时的速度分量U在个别范围内略低于雷诺数6 000时的速度分量。这可能是由于随着雷诺数的增加,需要相应增大摄像机帧数,导致图像分辨率有所降低,测量误差增大。特征线L=9 mm后,速度分量U开始降低,与图5所示的横截面矢量分布一致。由图6b可知,雷诺数对速度分量V的影响较为明显,随着雷诺数的增大,速度分量V逐渐升高,但不同雷诺数下的速度分布曲线非常相似。与内部子通道相同,y方向的速度分量大于x方向。3个雷诺数下的平均速度分别为0.036、0.065、0.101 m/s。

图5 雷诺数对内部子通道速度分布的影响Fig.5 Effect of Reynolds number on cross flow in interior subchannel

2.3 横向流动演变过程分析

本文选取内部子通道6和边壁子通道10,分析横向流速的分布及发展过程。所选取的雷诺数为9 000,对应轴向速度为0.6 m/s。实验共测量了3个不同的横截面,相邻两个截面的轴向距离为38 mm,从出口向入口方向看,3个截面的绕丝位置如图7所示。

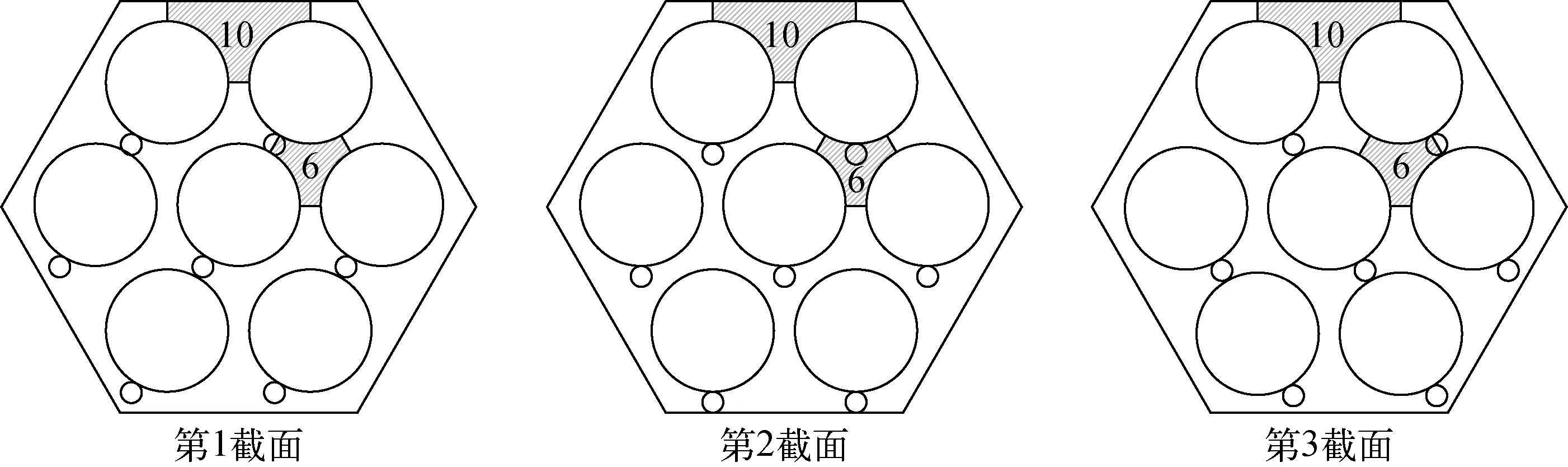
图7 不同横截面绕丝位置示意图Fig.7 Location of wrapped wires on different cross sections

内部子通道6和边壁子通道10的横流分布如图8所示。由图8a可知,第1截面在绕丝的迎风面产生了1个局部湍流涡,这是由流体与绕丝的相互作用而产生的。流体在顺时针方向的流动过程中,受到绕丝及其相邻两根棒的阻挡后反向运动,然后与流入的横流相遇碰撞,最终在绕丝迎风面形成1个逆时针的漩涡。在第2截面,绕丝逆时针旋转到子通道中心线位置。此时,绕丝并没有完全阻断横流,掠过绕丝的流体与顺时针的横流合并,向下流出子通道,并未形成湍流涡。当绕丝逆时针旋转到第3截面时,绕丝再次阻断横流,在绕丝的迎风面产生了部分回流。由图8b可看出,第1截面的边壁子通道产生了1个大尺度涡流。这是由于从12号角子通道进入10号边壁子通道的高速横流,与4号棒碰撞后分为两部分,一部分向右进入9号角子通道,另一部分向下进入11号内部子通道。后者的流动方向发生了90°变化,加之4号棒的绕丝将棒与棒的间隙完全挡住,增加了进入11号子通道流体的流动阻力,因此在5号棒的表面形成了1个大尺度涡。随着绕丝逆时针旋转,1号棒与4号棒的流动顺畅,边壁子通道的横流沿5号棒表面自然转向,所形成的大尺度涡逐渐消失。

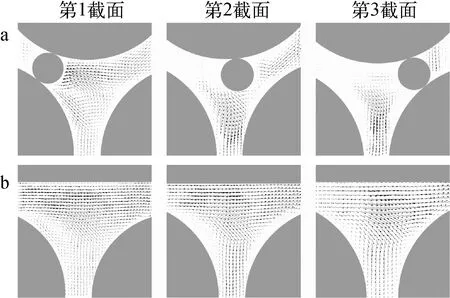
a——内部子通道6;b——边壁子通道10图8 不同截面横的流速度变化Fig.8 Variation of cross flow on different cross-sections

3 数值模拟

3.1 边界条件与网格划分

在实验研究的基础上,使用STAR CCM+软件对含绕丝7棒束内水的流动特性进行数值模拟分析,所采用的几何模型与PIV实验段相同。为减少计算量,数值模拟选取1个绕丝节距进行计算,长度为500 mm,流道进出口设置为周期性边界条件,模拟充分发展的棒束流动。流道内壁面与棒表面为光滑表面,设置无滑移边界条件。在绝热条件下以水为工质进行计算,温度为25 ℃,压力为101 325 Pa。对几何模型进行网格划分,经过网格无关性验证,最终选定的网格基础尺寸为0.8 mm,最小表面尺寸为0.12 mm,网格数为1 490万。

3.2 湍流模型敏感性分析

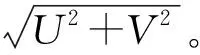
由图9可知,在所选取的8种湍流模型中,大部分湍流模型仅在某个特定范围内与实验数据吻合较好。综合分析,雷诺应力-椭圆混合模型预测的速度与实验数据更为接近,因此选取这一湍流模型的计算结果进行分析和研究。

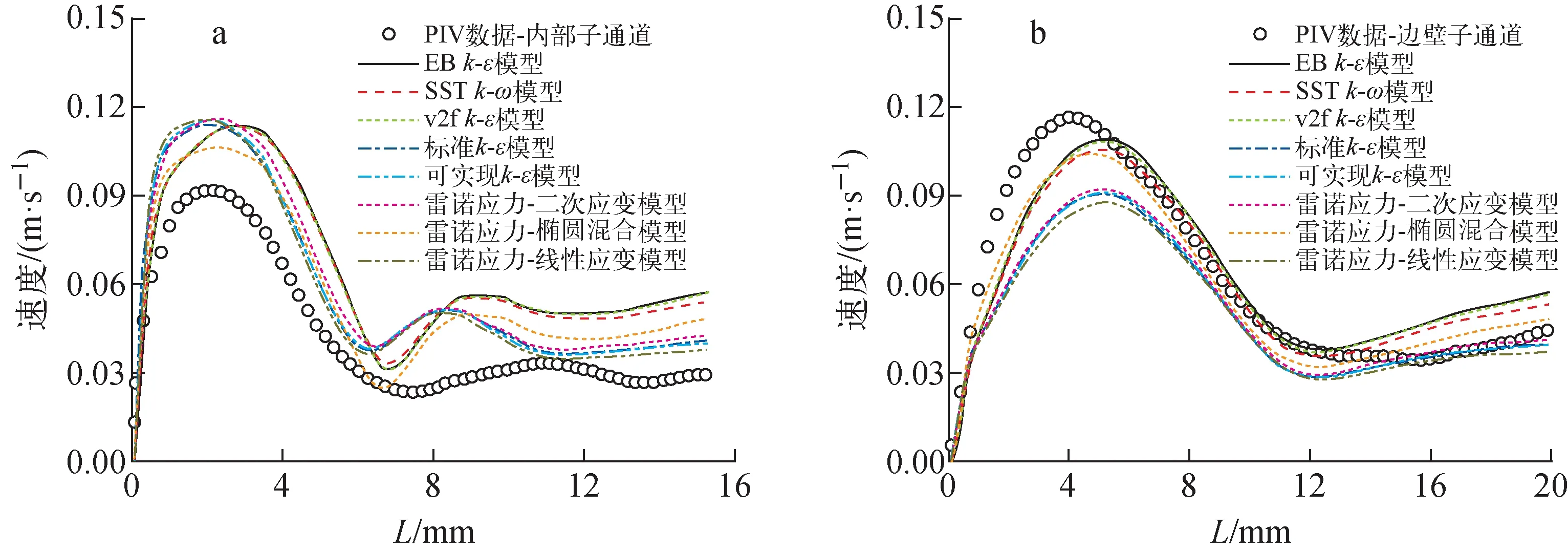
图9 不同湍流模型计算结果与实验数据的对比Fig.9 Comparison of experimental and numerical results

3.3 子通道间横流特征

(3)

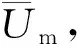
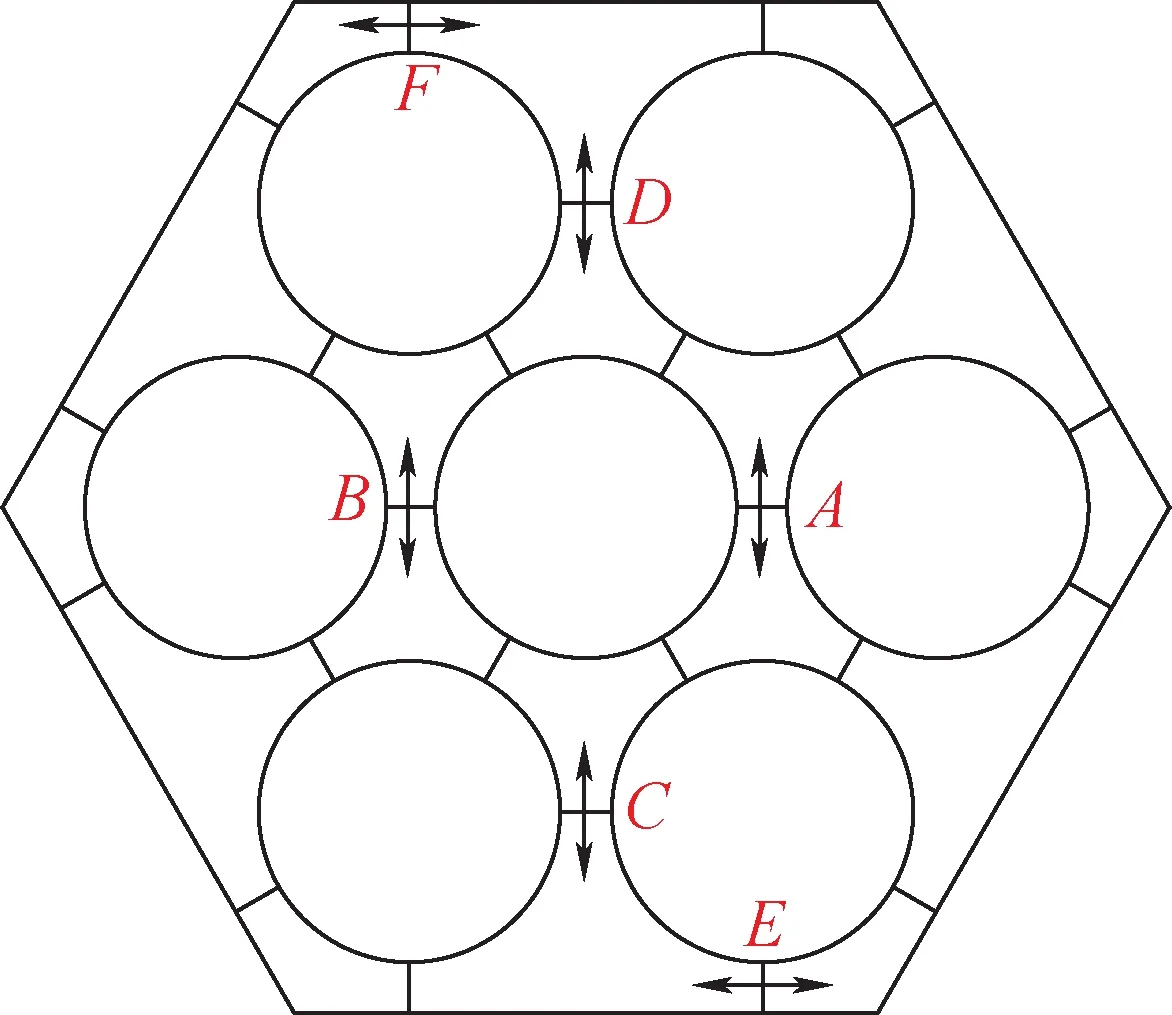
图10 不同类型子通道间隙特征线Fig.10 Characteristics lines between different subchannels

图11为不同类型子通道间的无量纲横向流速分布。由图11a可知,对于内部子通道之间的流动,横向流速基本在±0.25主流速度范围内。曲线的峰值是由于绕丝经过该间隙时,流通面积减小,使横向流速产生突变。由图11a还可看出,在1个节距(500 mm)内,横向流速突变两次,一次是由于棒自身的绕丝经过该间隙所致,另一次是相邻棒的绕丝经过该间隙所致。线A与线B的变化趋势和范围几乎相同,说明当内部子通道沿中心棒对称时,无量纲横向流速也呈对称分布。图11b为无量纲横向流速沿线C和线D的分布。由图11b可知,内部子通道与边壁子通道间的横向流动表现出与图11a相似的特征,无量纲横向流速的范围也在±0.25以内,两条曲线近乎重合。图11c为边壁子通道与角子通道的横流特性,与前两组曲线不同的是,虽然线E与线F的无量纲横向流速变化趋势相同,但正负不同,说明此时两个位置的横向流速方向相反。此外,无量纲横向流速在1个节距内只发生1次突变,说明角子通道之间的交混仅受本身的绕丝影响。

3.4 雷诺数对横向流动的影响

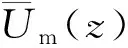
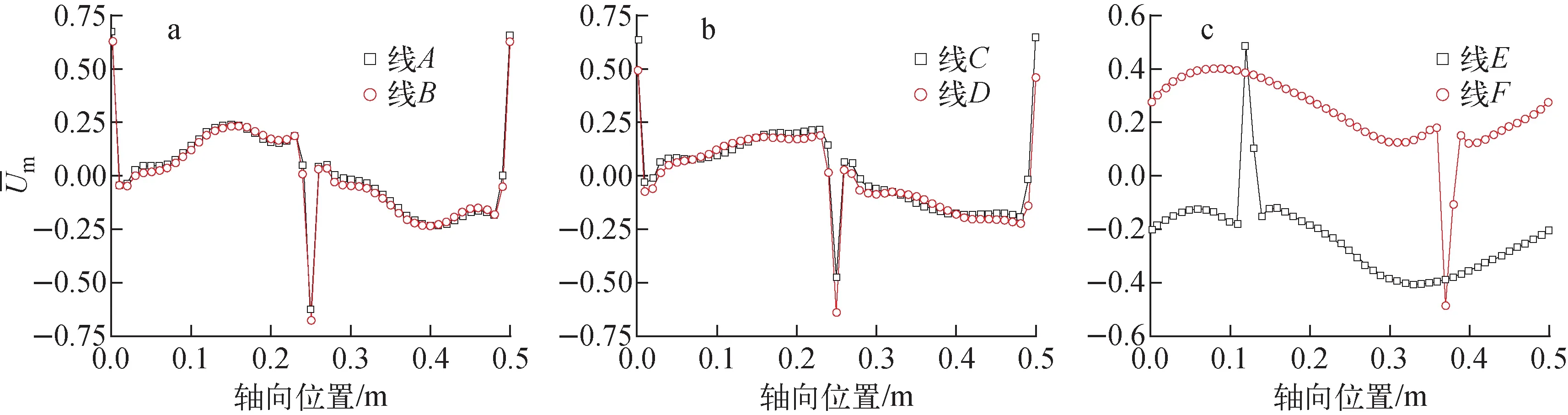
图11 子通道间无量纲横向流速分布Fig.11 Nondimensional cross flow between subchannels

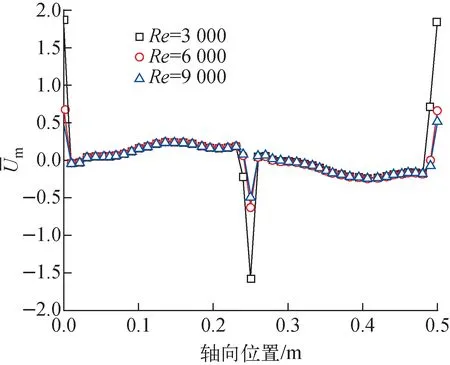
图12 雷诺数对子通道间无量纲横向流速的影响Fig.12 Effect of Reynolds number on nondimensional cross flow between subchannels

4 结论

本文采用PIV实验测量和数值模拟相结合的方法,对绕丝作用下棒束内的横向流动进行了研究,得到以下结论。

1) 含绕丝棒束内存在尺度不同的两类涡流:第1类是小尺度涡,由流体与绕丝碰撞所致,其主要出现在绕丝迎风面,旋向与横截面环流方向相反;第2类是大尺度涡,出现在棒束外围,主要是由于横向环流遇到棒的阻碍,部分流体转向90°后而在相邻棒的表面所形成。

2) 雷诺数对横向流速的分布规律影响明显,横向流速基本随雷诺数的增大呈线性升高的趋势。

3) 在所选定的参数范围内,雷诺应力-椭圆混合模型对棒束内横向流动的预测与实验数据吻合较好。

4) 子通道间的横向流动呈现一定的周期性,对于所选定的棒束和绕丝尺寸,无量纲横向流速在±0.25范围内,其分布规律与子通道类型及绕丝位置密切相关,但受雷诺数的影响较小。