邮轮建造过程中内装物资需求量组合预测

潘馨悦,杨家其,余欣怡,徐 靖

(1.武汉理工大学 交通与物流工程学院,湖北 武汉 430063;2.武汉理工大学 船海与能源动力工程学院,湖北 武汉 430063;3.上海外高桥造船有限公司 上海 200131)

邮轮实际建造过程中面临着诸多挑战,如生产组织方式复杂、建造周期长、造价高等,因此整个生产制造环节有很多待优化之处[1]。邮轮建造较普通船舶建造最具差异的环节就是内装过程。当前我国邮轮建造所需的内装物资大部分来源于进口,因此准确预测每期物资需求量,不仅能在生产部门发出订单需求时保证物资足量送到,还能降低集配中心的物资储存管理成本。准确预测能为决策制定提供重要的支撑依据。目前,学者对制造业中的物资需求预测已进行了不少研究,如船用钢材、民用航材的预测等[2-3],但对于船用内装物资的研究多从其如何选择及应用展开,较少有关其需求预测方面的研究,因此笔者考虑从其他物资需求预测出发,对内装物资需求量预测进行研究。

当前,学者已对物资预测方法进行了大量探索,包括指数平滑法、ARIMA模型及神经网络预测模型等,研究结论均证实了这些方法能在一定程度上提高物资预测的精度,便于物资管理部门做出准确的决策。指数平滑法在预测过程中对数据量的要求不高,并且能赋予不同序列以不同的权重,从而使预测值更接近真实值,但是对于中长期预测效果不太理想[4]。ARIMA模型灵活性较强,能够对稳定的具有季节特征的数据进行预测,预测效果可靠,被用于物流需求预测、交通量预测等方面,但其对于预测数据稳定性有较高的要求,故对于非平稳时间序列的预测精度表现一般[5]。神经网络因自适应性、容错能力强和大规模并行计算等优势被广泛应用于时间序列预测,但其又存在收敛速度慢、容易陷入局部最优等问题[6]。

上述单项预测方法通常是基于某一方面进行预测,仅能对某一方面提供有效信息。于是组合预测方法被提出,并被证实可以克服单项预测方法的局限性,提高整体预测过程准确度[7]。确定组合预测模型的核心有两个,即选择合适的单项预测模型和确定各模型的权重。目前组合预测方法中的权重大多是学者依靠经验选取,带有一定的主观性[8]。因此,为综合运用各单项预测模型的优势,笔者提出运用Winter指数平滑法、ARIMA模型及神经网络模型对邮轮建造过程内装物资需求量进行组合预测,通过比较基于各种权系数确定方法的组合预测结果,从而找到最适合内装物资需求量的预测方法。

1 内装物资概述

1.1 内装物资构成

内装物资主要来源于进口,其供应商主要以采购包形式进行供货[9]。按照采购包的不同对内装物资进行分类,如表1所示。

表1 内装物资分类

1.2 内装物资特性

邮轮建造过程所需内装物资的特性:①价值高昂,邮轮内装物资不仅在外观上表现出美观大气,在性能上还具有防潮、减震、抗噪、耐磨、易清洁等特点。由于部分物资(如酿酒设备、集气罩等)对存储条件要求严格,从而导致物资价值较高。②易燃性,通常设计者为体现邮轮的豪华,会考虑在客舱和大厅等区域铺设地毯、在天花板上悬挂装饰物等,因此具有较高的可燃性,从而给内装物资运输和存储过程提出了很高的要求。③依赖进口,当前国内船公司独立完成船舶内装工程还有一定的难度,与欧美国家在船舶内装环节、内装技术、内装环节配套资源上还存在较大差距。

总之,内装物资较普通船舶建造所用物资之间存在较大差异,因此在采购内装物资时除了要基于准确的预测值,还应考虑一定的库存以预防突发情况出现。

2 预测方法

2.1 单项预测模型

2.1.1 Winter指数平滑法

Winter指数平滑法属于预测模型中的一种,用于对含有多种成分的时间序列进行预测,Winter指数平滑法可表示为[10]:

S(t)=α(Y(t)-I(t-L))+

(1-α)(S(t-1)+T(t-1))

(1)

T(t)=β(S(t)-S(t-1))+(1-β)T(t-1)

(2)

I(t)=γ(Y(t)-S(t))+(1-γ)I(t-L)

(3)

(4)

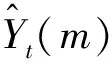
2.1.2 ARIMA预测模型

现实中待预测数据均多处于不平稳状态,即含有趋势、季节和循环等成分。因此对于此类数据,在选择模型之前需要对数据修正使其趋于平稳,同时还需要将其中的季节成分予以消除,通常将能对数据进行差分且平稳后的模型称为ARIMA(p,d,q)(P,D,Q)S模型,其中(p,d,q)为非季节部分,(P,D,Q)S为季节部分,S为季节周期的长度,具体如式(5)所示[11]。

Ft=α1Ft-1+α2Ft-2+…+αpFt-p+

et+β1et-1+β2et-2+…+βqet-q

(5)

式中:Ft为第t期的预测数据;α1,α2,…,αp为自回归系数;et为第t期的随机误差,也称白噪声序列;β1,β2,…,βq为移动平均系数。

2.1.3 神经网络预测

BP神经网络主要包含输入层、隐含层及输出层[12],具体结构如图1所示。其中,x1,x2,…,xm为输入;y1,y2,…,yn为输出;vir为输入层与隐含层的神经元之间的权重系数;ωjk为隐含层与输出层的神经元之间的权重系数;θr、μk分别为隐含层和输出层中的网络节点阈值。

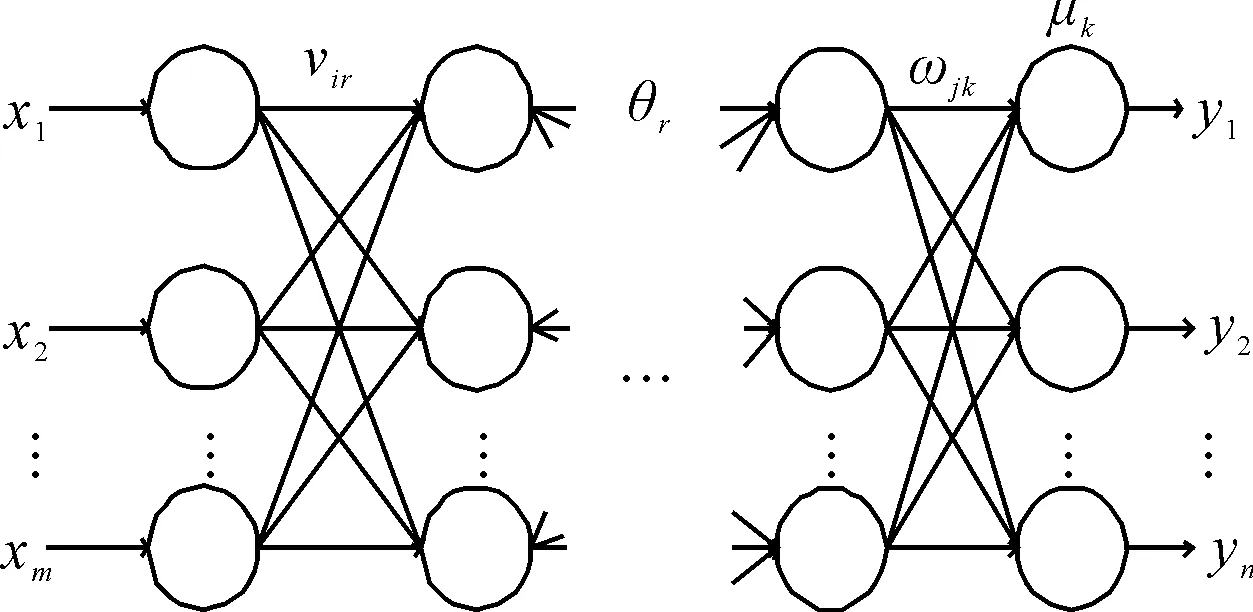
图1 神经网络结构图

2.2 组合预测模型

2.2.1 组合预测模型原理

假定某一预测问题在一定时段m的实际观测值为yt(t=1,2,…,m),对此进行预测共有n(n≥2)种预测方法。设fit为通过第i(i=1,2,…,n)种预测模型预测出的结果,则可建立以下组合预测模型[13]。

(6)

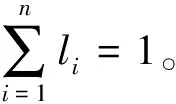
2.2.2 权系数确定方法

组合预测模型的关键在于如何确定各单项预测方法的权重,从而提高模型预测精度,常见权系数确定方法如表2所示。其中,eit为第i种方法的预测误差平方和,si为第i种预测方法的相对误差序列的变异程度系数,i=1,2,…,n。

表2 常见权系数确定方法

2.3 模型评价

为了对组合预测模型的效果进行评价,选取均方误差(MSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和均方百分比误差(MSPE)4个指标对模型进行综合评判。

(7)

(8)

(9)

(10)

式中:yt为t时刻的真实值;ft为t时刻的预测值。

3 实例分析

3.1 数据来源

为验证组合预测模型的可行性与有效性,以某船厂2019年7月至2022年3月邮轮建造过程内装物资需求量数据进行组合预测分析。

3.2 基于组合预测方法的实例验证

(1)Winter指数平滑法。利用软件SPSS24.0中时间序列预测的指数平滑模块,条件选择季节性中的“温特斯加性”,结果如表3所示。由表3可知,Winter指数平滑法的拟合优度R2为0.951,表明拟合优度很高;显著性为0.871>0.05,说明该时间序列能够被Winter指数平滑模型识别完全;离群指数为0,说明在该序列中没有出现有明显偏差的值。这些指标均说明模型拟合效果是可接受的。

表3 Winter指数平滑法统计量

(2)ARIMA预测模型。经过SPSS24.0软件差分后模型噪声残差的自相关图(ACF)和偏自相关(PACF)图分别如图2和图3所示,可以看出差分后时间序列的噪声残值均落于区间内,序列趋于平稳,最终确定使用的模型为ARIMA(0,1,0)(0,1,1)12。

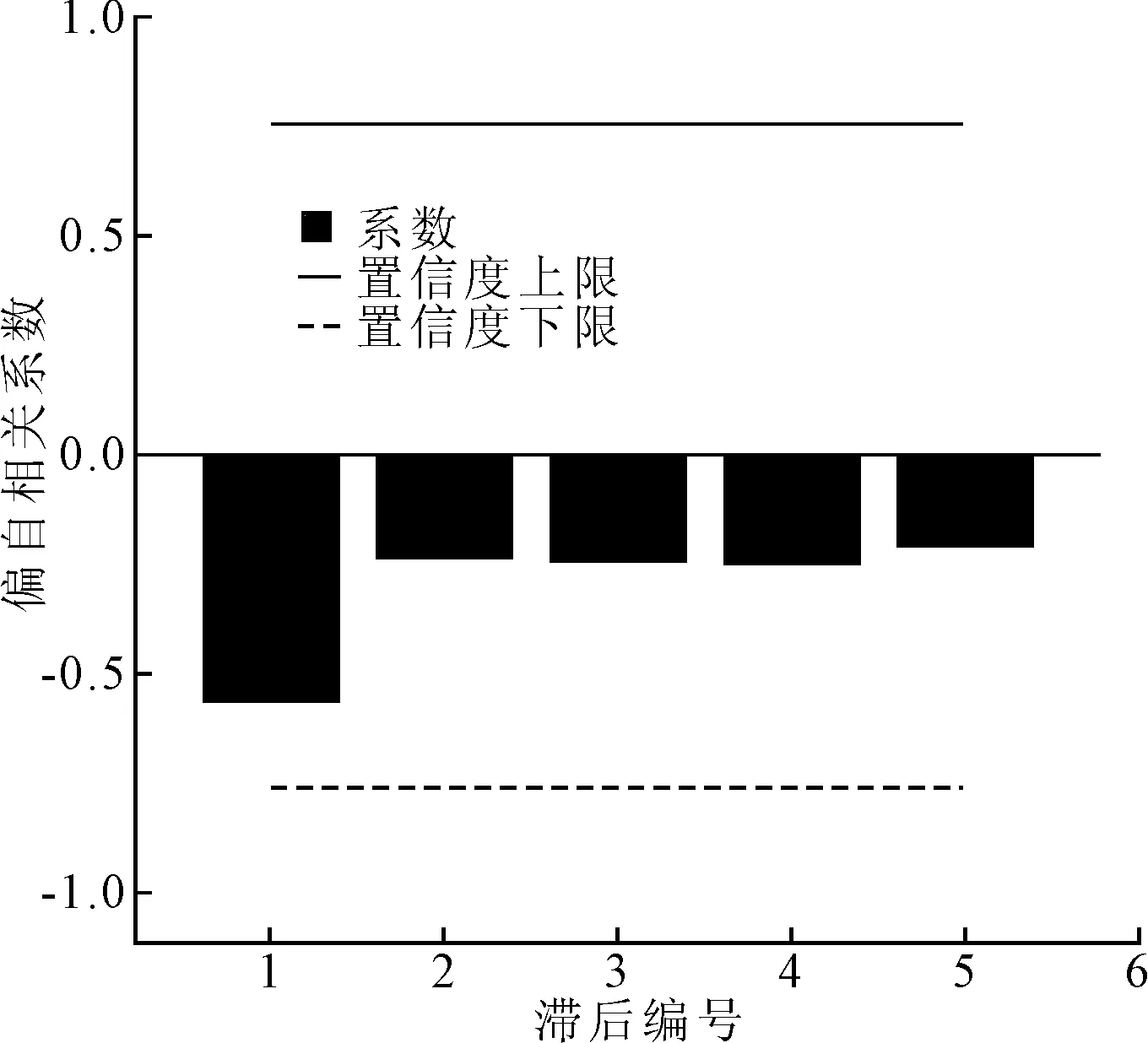
图3 模型噪声偏自相关图

经过模型ARIMA(0,1,0)(0,1,1)12的预测分析,所得结果如表4所示。由表4可知,该模型的拟合优度R2为0.784,大于0.700,拟合效果良好;显著性为0.937>0.05,说明该时间序列能够被ARIMA预测模型识别完全;离群指数为0,同样说明该序列中没有出现明显偏差的值,这些指标都说明模型拟合效果可接受。预测精度虽较Winter指数平滑法次之,但满足预测条件,同样可用于对内装物资需求量的预测。

表4 ARIMA预测模型统计量

(3)神经网络预测模型。神经网络预测过程通过Matlab软件实现。先对样本数据进行归一化处理,并设定输入节点的训练函数为Traingdx函数,确定Tansig函数为输入层与隐含层之间的激活函数,Purelin函数为隐含层与输出层之间的传递函数。同时设定学习速度为0.05,最大训练次数为1 000次,目标误差为0.01。训练误差表现如图4所示。最佳误差值在第1 000次时达到。经测算,R=0.891,说明模型拟合度较好,可用于对内装物资需求的预测。

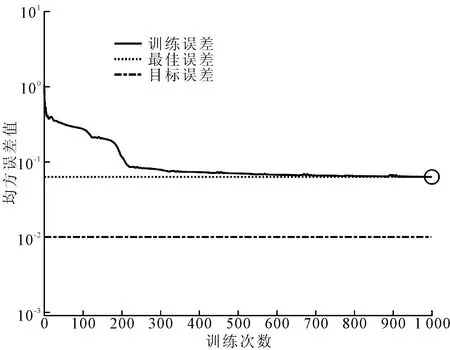
图4 神经网络训练误差图

综上,得到基于各单项预测方法的预测值和绝对误差,如图5所示。其中1表示Winter指数平滑法,2表示ARIMA模型,3表示神经网络模型。

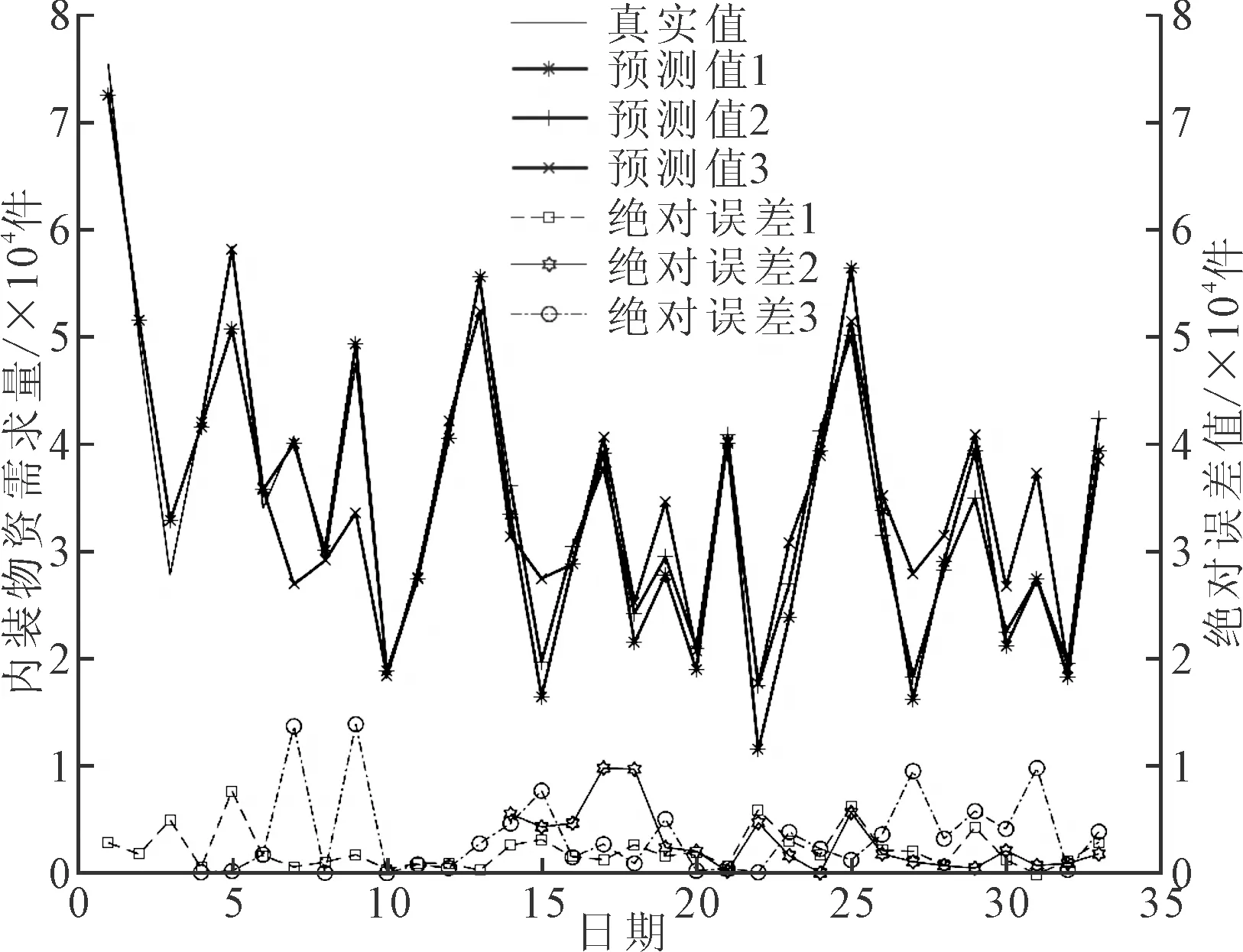
图5 各单项预测方法的预测值和绝对误差

(4)组合预测模型。根据前述权系数计算方法,得到不同方法下各单项预测方法的权系数,如表5所示。然后,对不同权系数计算方法下的组合预测值进行计算,并绘制相应的拟合图,如图6所示。由于组合预测值被准确计算出的前提在于各单项预测方法能够计算出数值,因此实际可计算出的为2020年8月—2022年3月的数值。

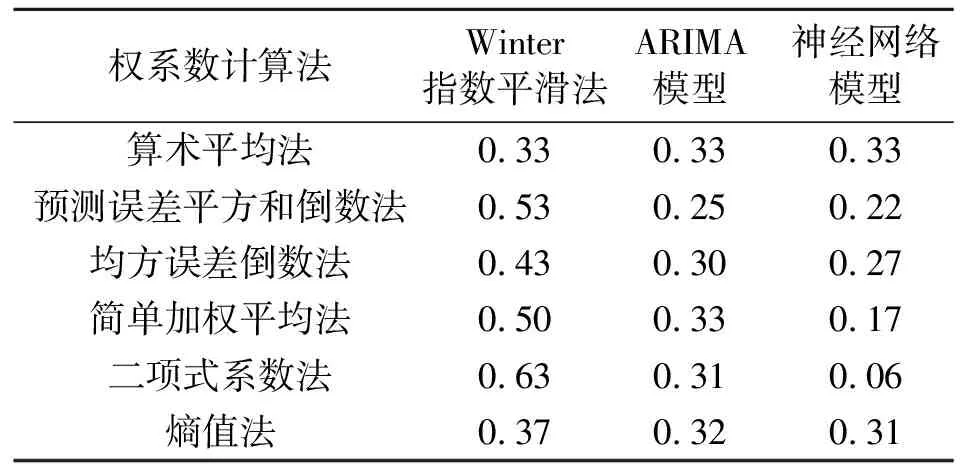
表5 各预测方法权系数

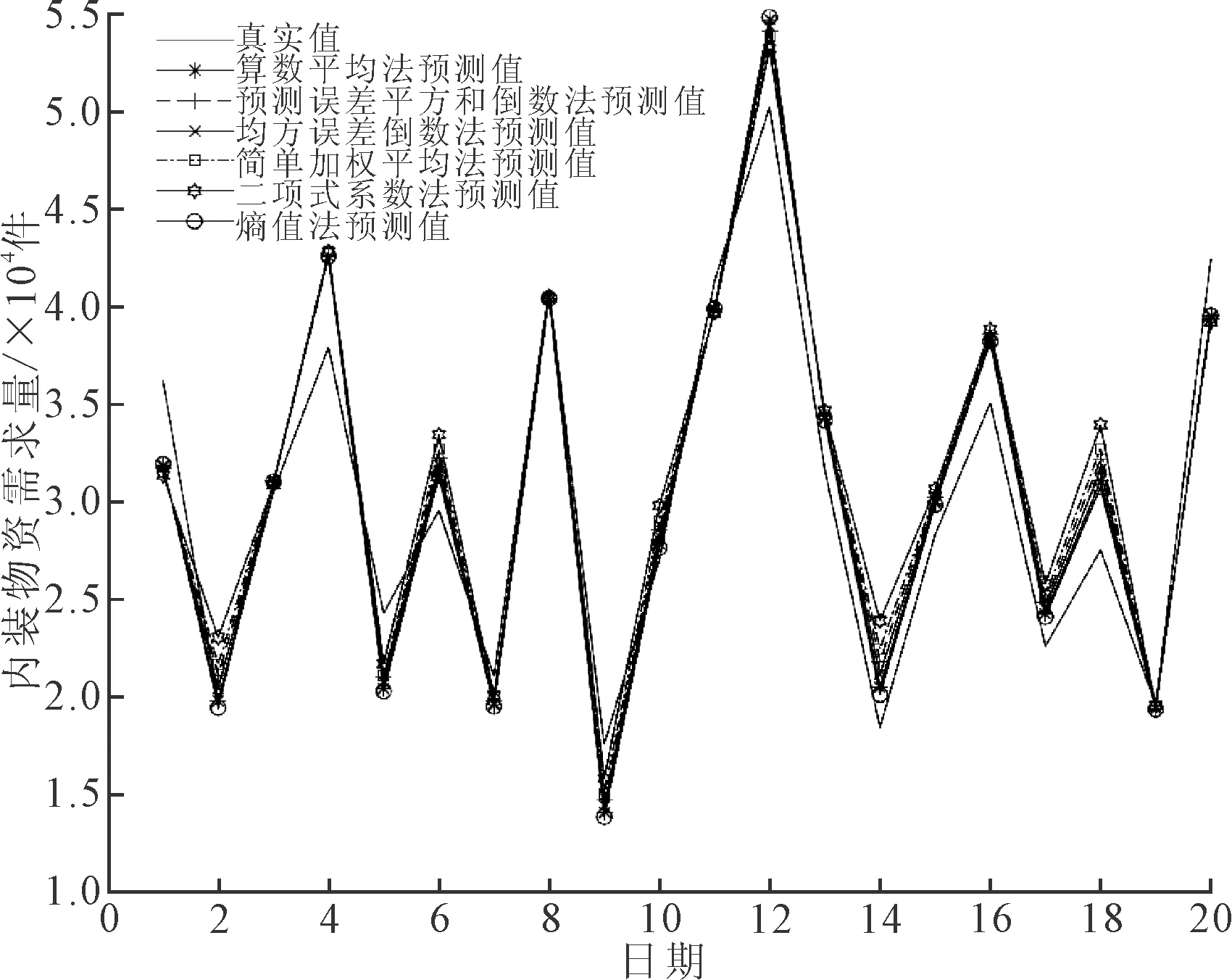
图6 基于不同权系数的组合预测值拟合图

3.3 预测模型评价

确定不同权系数的组合预测模型的表达式后,还需要对其进行相应的指标评估。根据式(7)～式(10)计算单项预测方法及组合预测模型的评价指标值,具体结果如表6所示。由表6可知:①对于单项预测方法来说,基于Winter指数平滑法计算出的各指标值最优,ARIMA预测模型次之,而经神经网络模型的预测效果不太理想。因此若只考虑单项预测方法进行预测时更倾向于选择Winter指数平滑法。②在组合预测模型中,基于熵值法的组合预测模型得到的各项指标值最优,基于二项式系数法的组合预测模型的预测效果最差。从各项指标值可以得到,在构建的组合预测模型中以Winter指数平滑法权系数在0.37附近、季节ARIMA法权系数在0.32附近、神经网络模型权系数在0.31附近变动得到的预测结果最为准确,预测效果最佳。

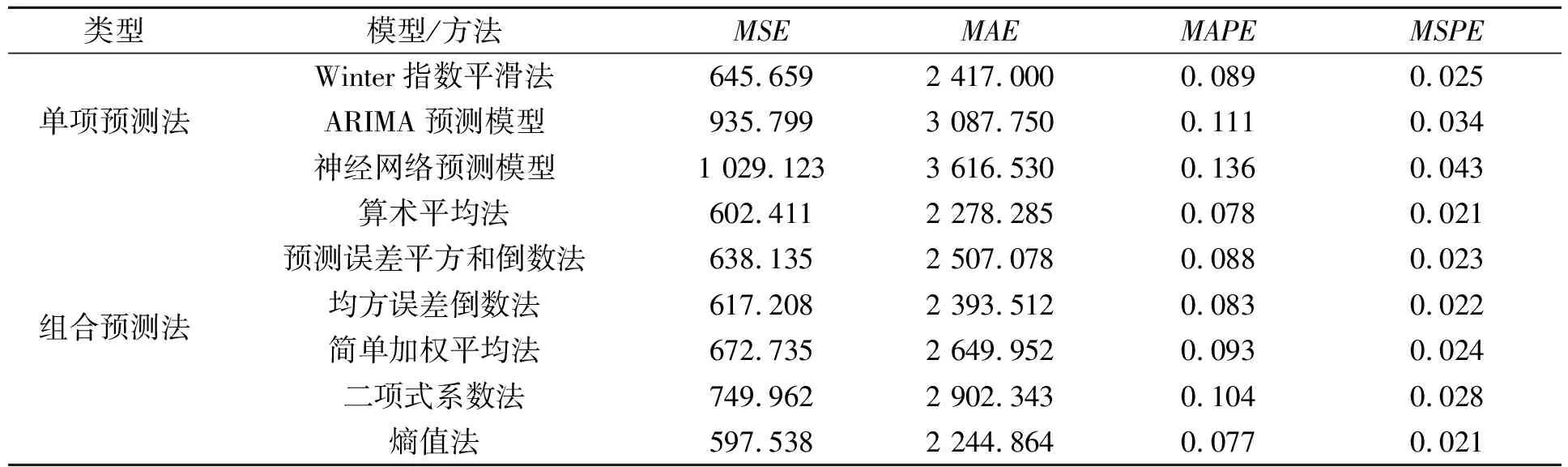
表6 评价指标值

4 结论

(1)针对邮轮建造过程内装物资需求量预测问题,构建了基于Winter指数平滑法、ARIMA模型和神经网络3种方法的组合预测模型,基于不同权系数的组合预测模型计算得到的指标值普遍以MSE<800、MAE<3 000、MAPE≤0.1、MSPE<0.03为主,优于单项预测模型相应指标值,证实了组合预测模型的有效性。

(2)经Winter指数平滑法计算出的MSE、MAE、MAPE、MSPE值优于基于简单加权平均法、二项式系数法的组合预测模型所对应的指标值,说明在组合预测模型中权系数的确定也会对最终预测结果产生影响。

(3)由于笔者选取的ARIMA模型进行了差分,因此经组合预测模型计算出的值还较少,对最终结果或将产生一定影响。后续将考虑寻求更优的预测方法解决内装物资需求量预测问题,并将预测结果用于内装物资库存控制研究。