考虑人员流动的矿山疫情传播规律研究

刘杰鑫,李墨潇,赛尔达尔·艾克拜尔,周 伟,徐雅玲,曾菲儿,张 斌

(1.武汉理工大学 中国应急管理研究中心,湖北 武汉 430070;2.武汉理工大学 安全科学与应急管理学院,湖北 武汉 430070;3.中能建绿色建材有限公司,湖北 武汉 430000;4.华中科技大学 新闻与信息传播学院,湖北 武汉 430074;5.武汉理工大学 航运学院,湖北 武汉 430063)

2020年年初,新型冠状病毒肺炎席卷而来,截至2022年9月20日,新型冠状病毒肺炎全球累计超6亿人确诊,超600万人死亡,仍现存确诊病例超1 200万例[1]。矿业作为国家战略支柱行业,受到疫情的影响巨大。虽然目前国内疫情得到控制,局面开始好转,但仍然持续性出现零星疫情爆发:例如新疆和硕县川硕矿山检测出27例无症状感染者,疫情发生后,矿山立刻停工停产,启动应急响应[2]。国外的疫情控制更是不容乐观,确诊与死亡人数仍呈上升趋势:例如玻利维亚最大矿山“圣克里斯托瓦尔”受疫情影响两度停产,在对公司8 093名工人和合同工进行检测后,发现了疑似病例168例,确诊病例41例[3];巴西矿业巨头“淡水河谷”旗下某一铁矿山确诊感染者至少200例[4];“必和必拓智利Escondida”铜矿矿场感染新型冠状病毒肺炎的人数已达94名[5]。截至2020年7月,有36个国家的275个矿山受到影响[6]。

由于矿山本身的资源性和商业性,其地理位置、设计属性非常不利于传染病的防控,主要有以下几方面特点:①地理位置偏远;②人员规模大;③矿山环境密闭程度高,通风条件较差;④医疗条件水平较低。因此,了解矿山中病毒传播机理,分析病毒在矿山中的传播过程,制定科学有效的矿山疫情防控措施成为迫切的现实需求。

传染病是在人群中发生的一个复杂的扩散过程,针对这一过程建立模型,可以更好地理解传染病的传播机理和认识其内在规律[7]。目前按照目标种群分类,研究传染病传播的模型主要分为单一群体、微观个体及复合群体3种[8-9]。其中,微观个体模型是对个体制定其自身属性和行为规则,通过个体之间形成的接触网络来模拟传染病发展过程。ADAM等[10]在模拟传染病流行的过程中应用了元胞自动机,讨论了疫情传播受人员流动性和就医及时性的影响;STEPHAN等[11]将概念验证模拟模型作为工具,通过重新参数化媒介子模型,对通过白纹伊蚊传播的登革热和基孔肯雅病毒进行了研究;EMANUELE等[12]将程式化的移动模式和手机数据驱动的移动模式整合到一个基于媒介的传播模型中,模拟了城市中媒介传播疾病暴发过程,研究了该方式的优势和局限性;万巧等[13]结合多源轨迹数据构建了能够准确描述微观个体交互的空间显式个体传播模型,通过登革热模拟结果对干预策略进行了评价;陈长坤等[14]建立了传染病跨区域传播的SIR模型,对传染病在跨区域传播时受动态区域所在方位和空间大小的影响及规律进行了探究;房志明等[15]考虑人员流动与病毒近距离接触传播,将其耦合构建了传染病传播模型,模拟了“钻石公主”号邮轮的病毒传播情况。

因此,笔者以传染病动力学理论为基础,结合矿山日常运行和传播环境特点,建立并开展不同日常运行条件下矿山内传播模型数值模拟仿真分析,讨论各风险因素对传染病在矿山中传播的影响,分析病毒在矿山中由于人员活动而引起近距离接触的传播过程,给出抑制矿山内病毒传播的建议,以期为当前疫情防控的紧迫形势下控制矿山内的传染病传播提供理论依据和决策参考。

1 模型建立

1.1 矿山人员流动模型

根据矿山相对密闭的实际情况,制定矿山人员流动模型的主要规则如下:①在规定的活动模式下给每个模拟人员随机赋予“时间-活动”序列及行为轨迹,如给一个模拟人员X赋予“时间-活动”序列为“7:00-食堂”,人员一天的运动轨迹假设为宿舍→食堂→矿井/办公楼→食堂→矿井/办公楼→食堂→宿舍,设定“5:00-起床”“6:00-吃饭”“7:00-上班”“12:00-吃饭”“13:00-上班”“18:00-吃饭”“19:00-回去睡觉”。②对于每个模拟人员,当到达了“时间-活动”序列中的某个时间时,相应的活动模式就被执行,且各模拟人员到达各场所的时间和次数符合“泊松分布”。

1.2 模拟矿山人员流动的传染病传播模型

以新型冠状病毒在矿山中的传播为研究对象,假设只有近距离飞沫和接触传播两种传播途径,并假设两种传播途径的病毒强度一致,其在矿山中的传播规则有以下几方面。

(1)矿山作为相对封闭的环境,人员流动场所复杂,且人数较多,病毒可通过感染者与易感者之间的密切接触来传播。提出如下假设:①该矿山在运营期间封闭管理且无人员调动,无人员出入矿山,矿山总人数保持不变;②矿山运营期间,感染者不会康复痊愈或死亡,即不会出现移除者;③感染者只会传染其他矿山人员,且矿山人员不与外界人员接触,所有人只在矿山内部流动。在矿山人员流动的传染病传播模型中,不同场所中传播密度不同,如式(1)所示:

(1)

式中:E为环境通风,随机械通风的功率变化而不断变化;r1为病毒强度,与病毒本身属性相关;V为场所空间系数,与场所内部人员流动及空气流通空间大小有关。

(2)随着人员的流动,人员之间相互密切接触,矿山人员传播病毒的概率如式2所示:

(2)

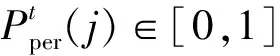
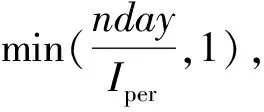
(3)设置初始携带者为1人。

(3)

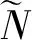
2 模拟与分析

2.1 环境通风对矿山中感染个体数的影响

假设矿山总人数为200人,按照安全规定,为保障环境最低安全通风量,功率应不低于30%,因此仅考虑E≥0.3的模拟情况,不考虑M,r2=0;分析不同环境通风情况下对矿山中感染个体数的影响,结果如图1所示。

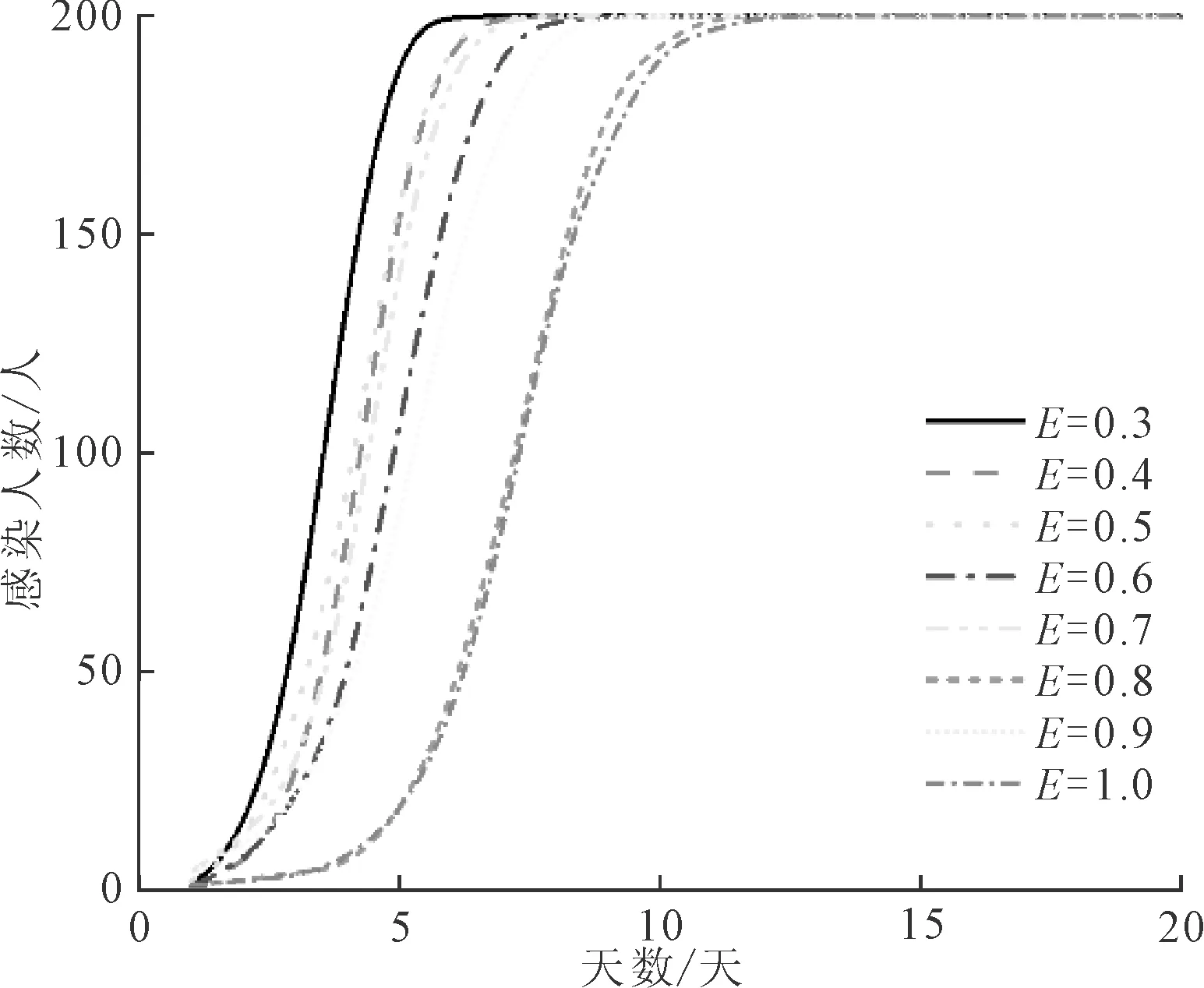
图1 环境通风对感染个体数的影响

由图1可知,大随环境通风E值增大,矿山全员被感染的时间从6天延长至 11天,相同感染个体数的感染时间均呈递增趋势,表明矿山中环境通风越好,越能抑制病毒的传播。当一天新增感染人数达到10人左右时,第二天开始感染人数会出现爆发性增长;当环境通风达到0.8时,感染爆发点较E=0.7时延后了2天,说明对病毒有较明显的抑制效果;而当E=0.6与0.7时,感染爆发点在同一天,说明两种状态对病毒的抑制效果相差不大。因此,可以将0.8作为环境的饱和通风量,通风机的功率保持在此状态下,既能够较好地抑制病毒传播,又能够相对减少能源的消耗。

2.2 矿山管控强度对矿山中感染个体数的影响

矿山总人数为200人,环境通风量处于安全通风量,即E=0.3,在矿山人员防护意识较差(r2=0)时,考虑矿山管控强度对感染情况的影响,模拟结果如图2所示。

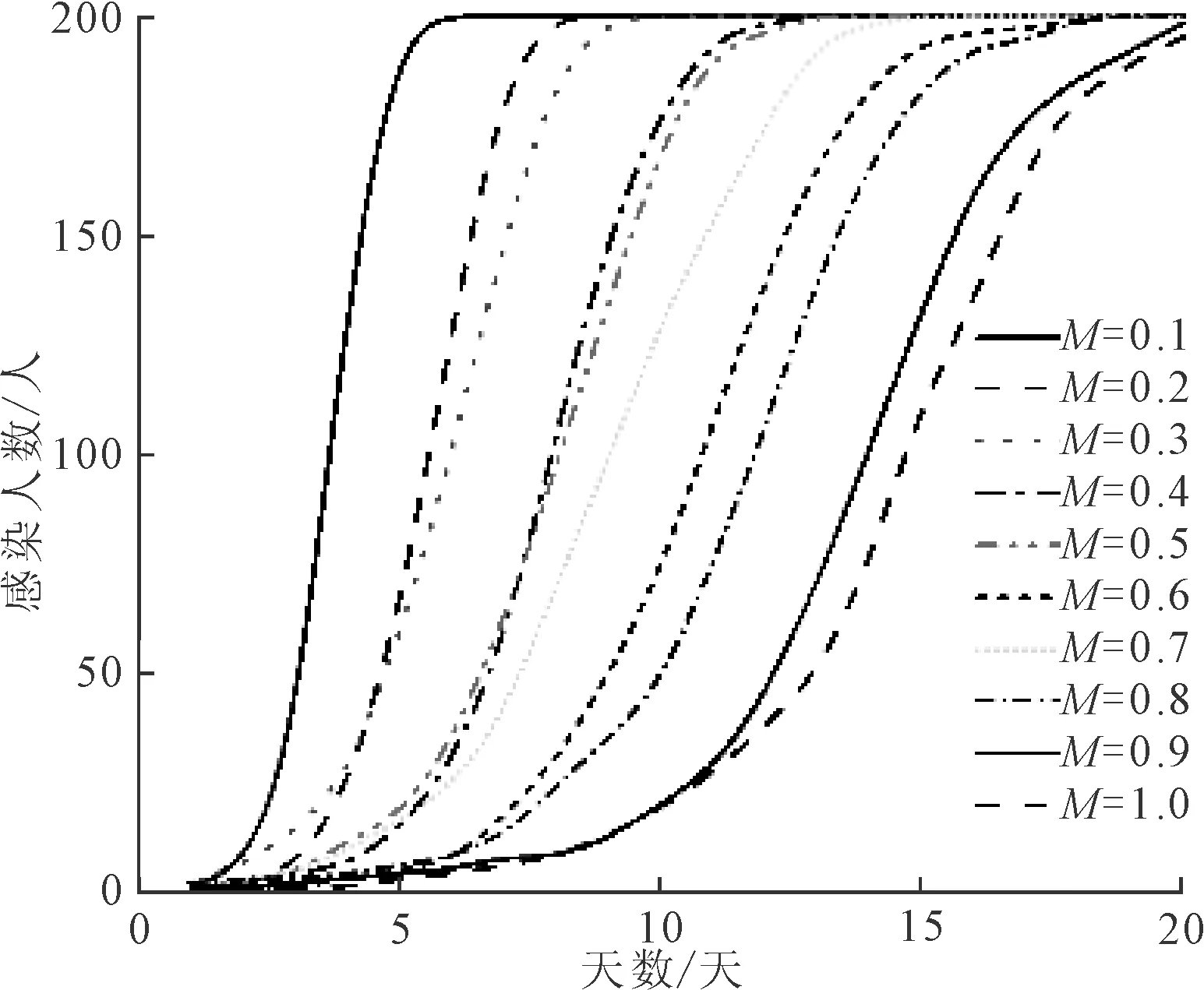
图2 管控强度对感染情况的影响

由图2可知,随矿山管控强度增加,感染爆发点出现时间逐渐延迟,感染人数增加的速度降低,对病毒传播产生抑制效果。在低管控强度(M<90%)时,对病毒传播的抑制效果并不显著;当达到高管控强度(M=90%)时,对病毒传播产生的抑制效果较显著;但M=100%时与M=90%时对病毒的抑制效果区别不明显。

2.3 矿山人员自我防护意识对矿山中感染个体数的影响

设定矿山仅保安全通风量,即E=0.3,不考虑管控强度M,取r2=0.0(未佩戴口罩)、r2=0.8(正确佩戴口罩),在矿山总人数为200时进行模拟分析,结果如图3所示。

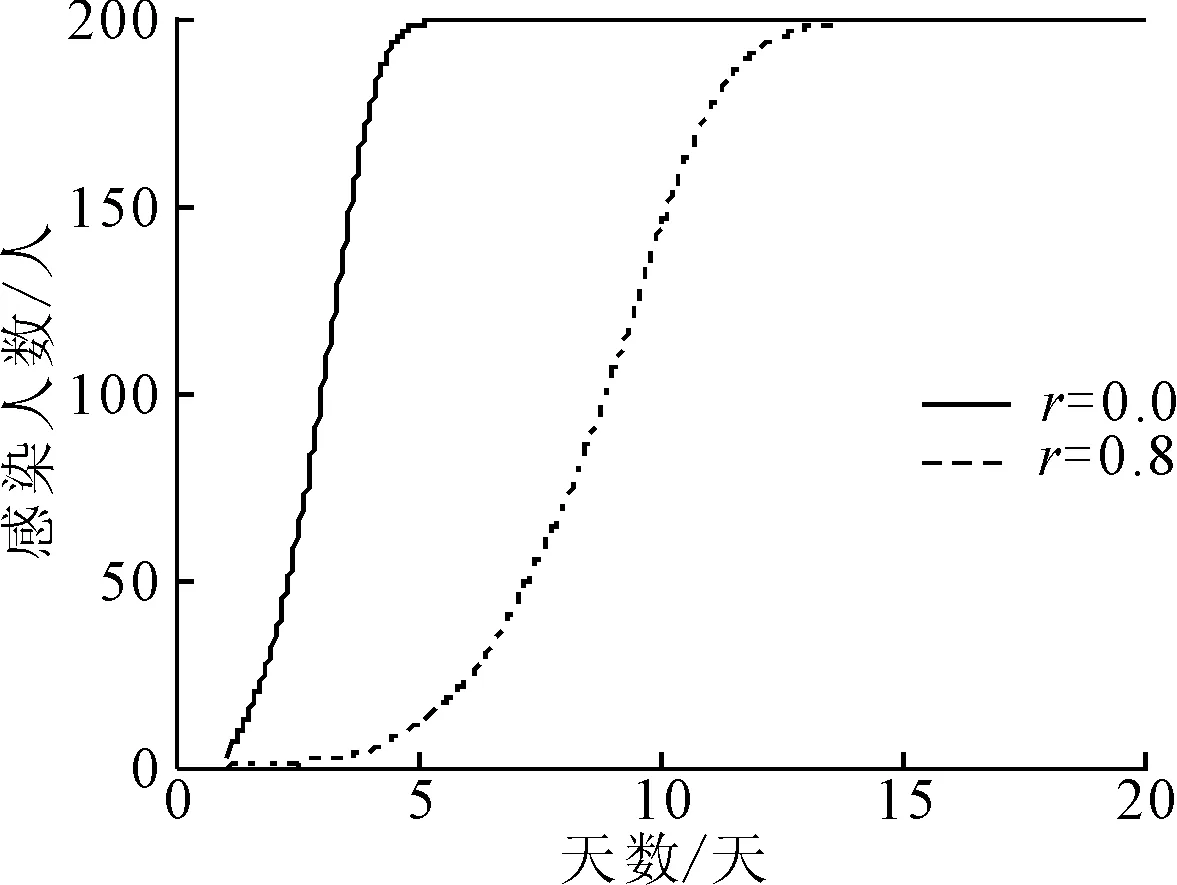
图3 人员自我防护意识对感染个体数的影响

由图3可知,未佩戴口罩(r2=0.0),矿山在第2天即出现感染爆发点,人员5天全部感染;而佩戴口罩(r2=0.8),矿山人员在第7天才出现感染爆发点,第14天才全部感染。说明矿山人员佩戴口罩后病毒传播速度显著降低。

2.4 矿山人员数量对病毒传播影响

结合相关文件和实际情况,根据人数来区别不同规模矿山,分别选取不同规模的矿山来进行模拟,分别考虑矿山全体人员个人防护意识较强(r2=0.8)及较弱(r2=0.0)两种状况;同时,矿山在保持安全通风量的情况下并未采取任何管控措施,因此E=0.3,不考虑管控强度M,结果如图4～图5所示。

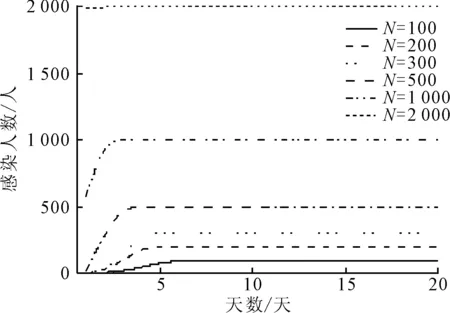
图4 未戴口罩时不同矿山规模感染情况

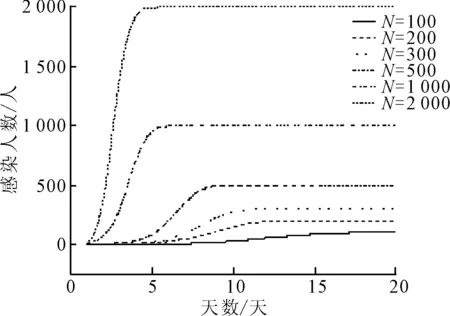
图5 戴口罩时不同矿山规模感染情况

由图4和图5可知,当矿山人员数量为100人时,两种情况下感染爆发点分别出现在第3天和第10天,在第8天和第20天时,全部人员被感染;当矿山人员数量为2 000人时,感染爆发点分别出现在第1天和第2天;矿山人员数量从100人增加至2 000人的过程中,爆发感染点逐渐提前,矿山人员全部被感染的时间逐渐缩短,说明病毒随着人数的增加传播速度加快。

3 结论

(1)环境通风对病毒传播有抑制作用,但随着其不断加强,抑制效果逐渐放缓,环境存在饱和状态,在该状态下既能够有效抑制病毒的传播,又能够减少能源的消耗,降低矿山日常运营成本。

(2)管控强度存在阈值和饱和值,矿山管控强度不能低于90%,可在90%～100%间调整,不必时刻处于紧绷状态,做到张弛有度。

(3)矿山人员自我防护意识是影响矿山传染病病毒传播的重要因素。在防控时期,矿山相关管理人员应加强对全体矿山人员自我防护意识的培养,养成正确佩戴口罩的习惯。

(4)矿山人员数量与病毒传播速度成正相关。疫情期间,矿山运营时应注意矿山人员规模,可采取分批、分时段工作的方式来控制人员数量。

(5)各因素中最敏感的因素是矿山人员自我防护意识,矿山在做疫情防控工作时最应该注重培养矿山人员自我防护意识,要求矿山全体人员正确佩戴口罩。