A Class of Simple Modules for Electrical Lie Algebra of Type D5

CHEN Yulu(陈雨露), SHEN Ran(申 冉)*, ZHANG Jiangang(张建刚)

1 College of Science, Donghua University, Shanghai 201620, China

2 College of Science &Mathematics, Shanghai Normal University, Shanghai 200233, China

Abstract：The simple modules for electrical Lie algebra of type D5 were investigated. The sufficient and necessary criteria of the simple Z-graded highest weight modules were established by means of determining the singular vectors of the Verma modules. The simple highest weight module is isomorphic to either that for the symplectic Lie algebra sp4 or Verma module.

Key words：electrical Lie algebra; simple module; highest weight module

Introduction

We denote the sets of all integers, nonnegative integers, and complex numbers byZ,Z+, andC, respectively. And we denote the universal enveloping algebra of Lie algebraεoverCbyU(ε).All vector spaces and algebras are overCthroughout this paper.

The study of electrical networks could trace back more than a century when Ohm and Kirchhoff researched electrical circuits. It remains a classic object in many branches of mathematics such as graph theory[1], as well as a wide range of applications in materials science and medical imaging[2]. Electrical Lie algebras, originating from the study of two operations, namely, adjoining a boundary spike and adjoining a boundary edge to a circular planar electrical network[3], were introduced by Lametal.[4]who gave the definition of electrical Lie algebras of finite Dynkin type and the electrical Serre relations. They mainly studied the electrical Lie groups and the structure of electrical Lie algebras of typeA2n.And the simple modules ofεA2n≅sp2nhave been studied in Ref. [5]. They also showed that the electrical Lie algebraεG2was six-dimensional and conjectured that the dimension of the electrical Lie algebra of typeXcoincided with the number of positive roots |Φ(X)+|, whereΦ(X)+was the set of positive roots ofX.

Su[6]proved the dimension conjecture of electrical Lie algebras for classical types and studied their structures. He showed thatεA2n+1≅sp2n+1,εBn≅εAn⊕εAn-1andεC2n≅εA2n(Vλ⊕V0), whereV0was the trivial representation andVλwas the simple highest weight representation for the symplectic Lie algebrasp2n.Therefore, the structure ofεA2n+1was obtained since that ofsp2n+1had been studied[7-8]. The universal enveloping algebra ofεA2n+1, also known as a symplectic oscillator Lie algebra or Jacobi Lie algebra, is an infinitesimal Hecke algebra[9-10], and the categories of weight modules forεA2n+1were classified in Ref. [11].

Recently, Gaoetal.[12]studied the structure and representations forεD4.They showedεD4≅sl2was a 3-step nilpotent Lie algebra constructed from the colored complete bipartite graphK2,2with coloring mapc, and classified all the simple highest weight modules. Besides, they provedεG2≅sch⊕Cz, whereschis the centerless Schrödinger algebra. Thus the representations forεG2were known as those for Schrödinger algebra, which were well studied in Refs.[13-17].

The electrical Lie algebra of typeD5is isomorphic to the semidirect product ofsp4with a 2-step nilpotent Lie algebra constructed from the colored 4-order tournamentT4.

In this paper, the electrical Lie algebraεD5is viewed as aZ-graded Lie algebra since it has more practical applications. And we study a class of simple highest weight modules for it. The paper is organized as follows. In section 1, some basic definitions and results are collected. In section 2, we give the classification of a class of simple highest weight modules forεD5.And in section 3, we get some conclusions.

1 Preliminaries

In this section, the definition of electrical Lie algebra for typeXand a spanning set of it were given in Ref. [4] as follows.

Definition1LetXbe a Dynkin diagram of finite type, andA=(aij) be the corresponding Cartan matrix. Define the electrical Lie algebraεXof typeXto be the Lie algebra generated by {ei}, whereiruns over the vertex indices inX, modulo the relations

We studied the structure ofεD5and gave the following structure theorem.

Theorem1We claim that

εD5≅sp4g(T4,c)

with basis

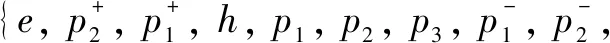
wheresp4is the symplectic Lie algebra andg(T4,c) is a 2-step nilpotent Lie algebra constructed from the colored 4-order tournamentT4.The brackets ofεD5are defined in Table 1.

2 A Class of Highest Weight Modules for εD5

The electrical Lie algebraε=εD5is a direct sum of the subalgebra isomorphic tosp4and an ideal. It isZ-graded with respect to the adjoint action ofh.Fori∈Zwe set

εi:={x∈ε|[h,x]=ix},

ε0:=spanC{h,p1,p2,p3,v1,v2,w1,z},

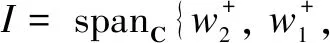
Anε-moduleMis called the highest weight module if there is a vector1λsuch thatM=U(ε)1λ,ε+1λ=0, andh1λ=λ1λ, whereλ∈C.Thus in other wordsM=U(ε≤0)1λ.Then

is a basis ofMdue to the Poincaré-Birkhoff-Witt Theorem.

LetMbe a simple highest weightε-module with the highest weight vector1λ.Verma module overεis the1-dimensionalε+⊕ε0-module defined by

ε+1λ=0,h1λ=λ1λ,p11λ=λ11λ,p21λ=λ21λ,p31λ=λ31λ,

v11λ=μ11λ,v21λ=μ21λ,w11λ=μ1λ,z1λ=c1λ,

where (λ,λ1,λ2,λ3,μ1,μ2,μ,c)∈C8.

From Table1, we obtain the following lemma.

Lemma1Claim that

λ1=λ2=λ3=μ1=μ2=0,

and

μ=c.

ProofFrom Table 1, we know that

Hence

which impliesλ2=0.Similarly,λ1=λ3=μ1=μ2=0.

Then from

w1-z=[v1,v2]=v1v2-v2v1,

we have

(w1-z)1λ=(μ-c)1λ=(v1v2-v2v1)1λ=

(μ2μ1-μ1μ2)1λ=0,

and

μ=c.

Hence the Verma moduleV=V(λ,μ), where (λ,μ)∈C2.

Any simple highest weight module with the highest weight vector1λis a simple quotient ofV(λ,μ).Therefore, to classify the simple highest weightε-modules, it suffices to classify all simple quotients ofV(λ,μ).Thus we determine the maximal proper submodules forV(λ,μ).

The following identities can be proved through direct computations.

Lemma2Fork∈Z+, we have

We discuss the simple highest weight modulesMin two situations:μ=0 andμ≠0 as follows.

Proposition1Mis isomorphic to a simple highest weightsp4-module forμ=0.

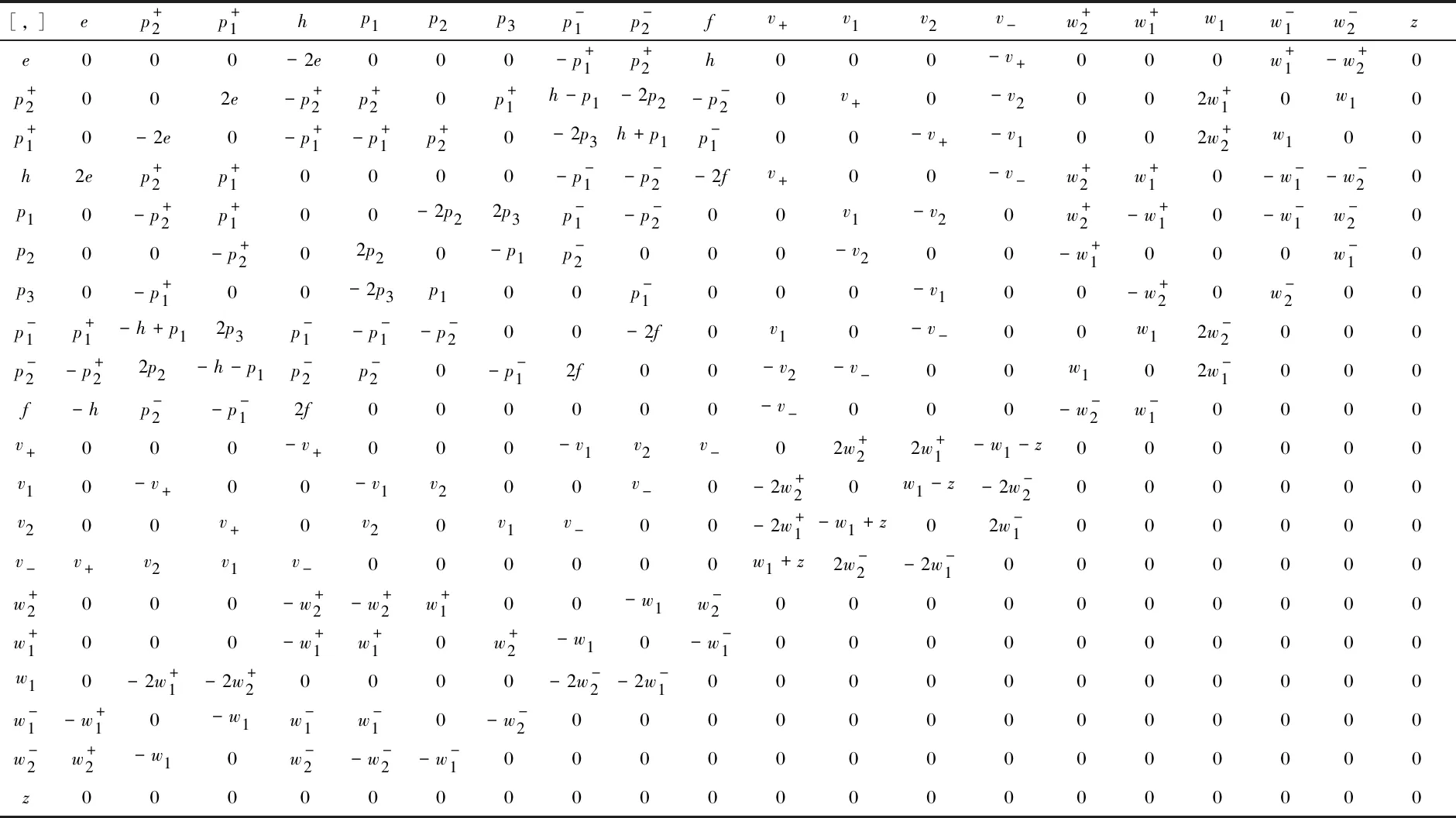
Table 1 Brackets in εD5

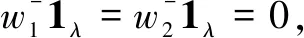
which is a nonzero proper submodule. It forces

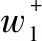
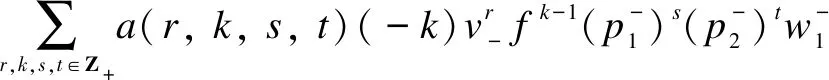
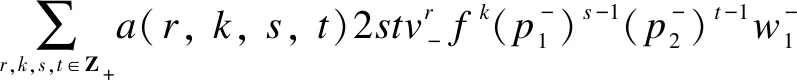
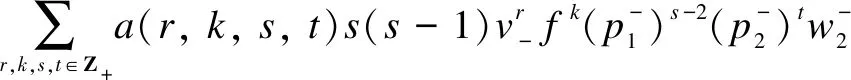
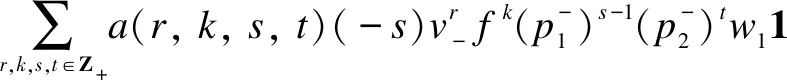
wherea(r,k,s,t)∈C{0}=C*.Similarly

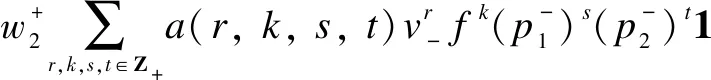
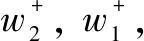
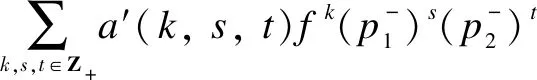
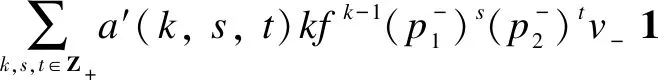
Therefore,Mis isomorphic to a simple highest weightsp4-module, which was studied in Ref. [18] with two fundamental weights,L1andL2.

Proposition2Verma moduleV(λ,μ) is irreducible ifμ≠0.

ProofRecall that a vectoruis called a singular vector in a moduleV(λ,μ)ifε+u=0. It may be written in the form

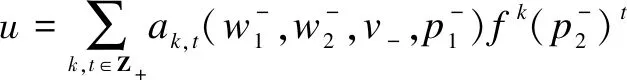
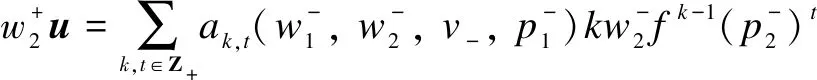
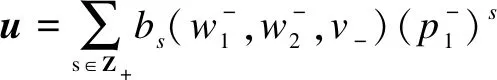
0=

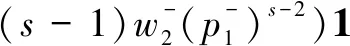
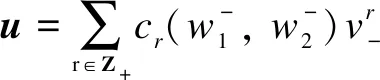
1λ,

1λ,

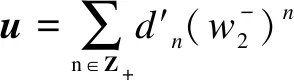
1λ,

we know thatn=0.Thus,u∈C1λ, and the theorem follows.

To summarize, we classify a class of the simple highest weight modules forεD5as follows.

Theorem2LetMbe a simple highest weightε-module with the highest weight vector1λ.For (λ,μ)∈C2,V(λ,μ) is the Verma module overε.

(1) Ifμ=0, thenMis isomorphic to a simple highest weightsp4-module.

(2) Ifμ≠0, thenM≅V(λ,μ) sinceV(λ,μ) is irreducible.

3 Conclusions

In this paper, we classify the simpleZ-graded highest weight modulesMfor electrical Lie algebra of typeD5.We seek singular vectors to determine the maximal proper submodule of Verma moduleV(λ,μ).Then the sufficient and necessary criteria for simple modules are obtained.

Ifμ=0,Mis isomorphic to a simple highest weightsp4-module, which has two fundamental weights,L1andL2.The highest weight module of the symplectic Lie algebrasp4is irreducible if it is the module with the highest weightL1,L1+L2, 2L1or 2L1+L2.Ifμ≠0, we haveM≅V(λ,μ), whereV(λ,μ) is irreducible.