基于正负分频信号的测速与测距方法

张云骥 蔡玖良

（南京电子技术研究所 江苏省南京市 210039）

线性调频信号是广泛应用到雷达技术领域中的一种信号形式，它通过脉冲压缩技术解决了作用距离与分辨率的矛盾，但其脉冲压缩后的时频耦合现象却导致无法准确获取目标距离，必须先要精确速度补偿后才行。在复杂探测场景下，尤其是在导弹群目标场景下或无人机群目标场景下，多目标的速度与距离的高精度测量一直都是棘手问题。

近年来随着雷达体制的进步、时频多子码和航天技术的发展[1-3]，雷达高精度测速与测距重新引起思考。文献[4]用到了正负斜率LFM 信号的多普勒频移的对称特性，但需要通过动目标检测实现精确测速，况且只适用于单目标场景。文献[5]使用对称三角线性调频信号实现超高速目标测速，但多目标的匹配则是在目标间距几十公里、可转化为单目标场景的条件下进行的，实际应用受限；另外，仅用幅度作为匹配元素的方法也容易引起目标误配。

针对以上问题，本文将对称三角线性调频信号设计改进，使之正负调频两部分频域可区分并留足余量（简称多普勒余量），形成一种新型分频信号（简称正负分频信号），可以有效解决匹配滤波的交叉峰值对参数测量的不利影响；同时，为了保证多目标场景下的目标匹配及参数测量精度，本文提出一种使用包含了目标幅度、包络熵和角度等信息的特征向量进行目标匹配的方法。本文所提波形和高精度测速测距方法原理简单、容易实现，仅用单个脉冲便可求出多个目标的无模糊速度和距离。

1 信号模型

正负分频信号是一种简单的复合调制信号，它的时频曲线如图1 所示。

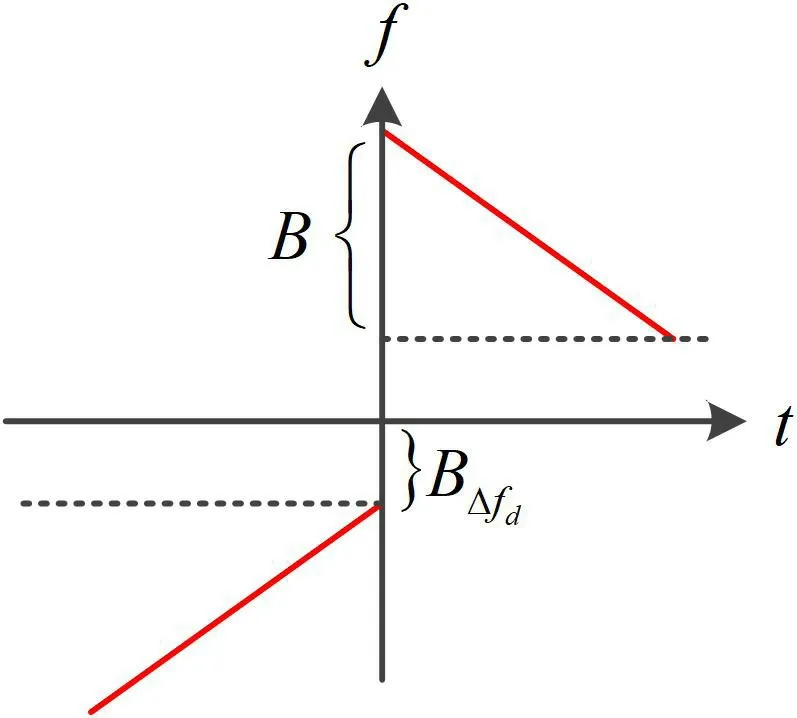
图1： 正负分频信号的时频曲线

两段LFM 信号的带宽、时宽相同，但调频率互为相反数。正负分频信号可以表示为：

经距离为R、速度为v的点目标反射和接收机解调到基带上的回波近似为：

图2： 频域脉压示意图

2 测速与测距算法设计

本节主要讨论基于正负分频信号实现目标精确测速与测距的基本原理，以及在实际工程中快速实现多目标高精度参数测量的算法流程。

2.1 测速与测距原理

由上节讨论可知，正负分频信号经频域分割并脉压后的目标峰值位置分别为：

2.2 多目标的速度与距离测量方法

当雷达探测波门内有多个目标时，信号脉压后就会出现多个峰值，如果s0(t)与s1(t)中的峰值位置配对不准，就会影响目标速度与距离的测算。

考虑到在多目标场景下，目标的空间位置（距离R、方位角φ、俯仰角θ）、运动参数（速度v）、散射能量（幅度A）和外观形状（包络熵E）会有所差异，可用这些参数构造目标特征向量，可从和差差波束中获取。

2.2.1 特征向量的构建

根据式（7）和式（8），多目标回波的脉压结果可以简写为：

两点之间的距离越近，匹配程度越高，距离最近的两点若满足阈值条件便可认为匹配成功，进而能算出该目标的速度和距离。据此可以形成多目标的匹配与参数测量的Clean 算法，简述如下：

第一步：根据式（19）计算集合P 中当前最强点Pi与集合Q 中所有点的距离；

第二步：选择距离最近的两点作为匹配成功的最强目标，根据式（11）和式（12）计算当前目标的速度和距离R；

第三步：将P、Q 两集合中的当前匹配点清除，进行下一目标的匹配和参数测量；

第四步：依次迭代，直至目标数量满足条件或两集合再无可配准目标为止。

整个基于正负分频信号的多目标测速与测距流程如图3 所示。

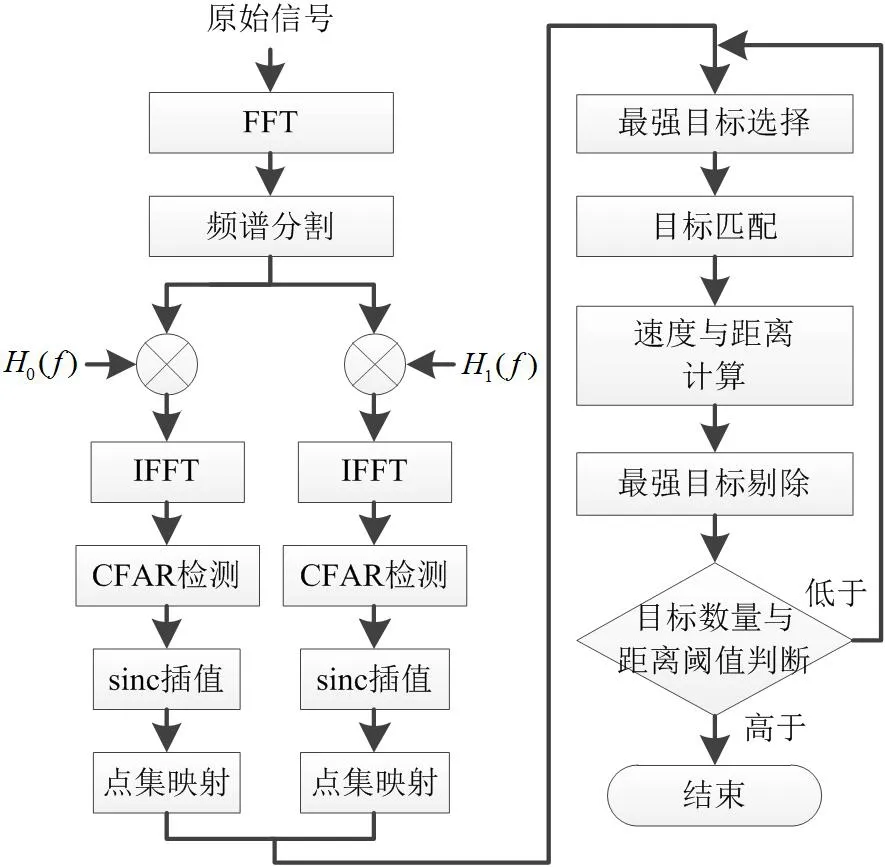
图3： 基于正负分频信号的多目标测速与测距流程图

3 实验仿真和结果分析

本节将针对单目标场景和多目标场景两种不同的探测场景进行仿真与计算。实验仿真时，设定光速c=3e8 m/s，选用X 频段雷达典型的波形参数如表1 所示。

表1： X 频段雷达典型的波形参数

3.1 单目标场景

在雷达参数和场景参数一致的条件下，分别用基于对称三角线性调频信号的测量方法和本文基于正负分频信号的测量方法得到目标速度与距离的测量结果如图4所示。

图4： 速度与距离测量误差

从图4(a)可以看出，对称三角波在波峰不可分辨的低速条件下无法测速，同时测速误差也会随着速度的增大而增加；而正负分频信号无论是在低速还是在高速条件下都能准确测速，且测速误保持稳定。从图4(b)可以看出，使用对称三角波进行距离测量时因其方法忽略了距离-多普勒耦合的高次项，导致测距误差仍然会随着速度的增大而增加；而使用本文方法得到的测距误差却不会随着速度的增大而发生恶化。可见，用正负分频信号进行速度与距离测量，结果明显更优。

为近一步宏观考察本文方法的速度与距离测量精度和目标匹配性能，在该模拟场景中选取v=4200 m/s、R=100 km 的位置，并设置信号脉压后的平均信噪比，在每一种信噪比下用两种测量方法各自进行蒙特卡罗模拟1000 次实验，统计得到的速度与距离测量误差、目标匹配结果如图5 所示。

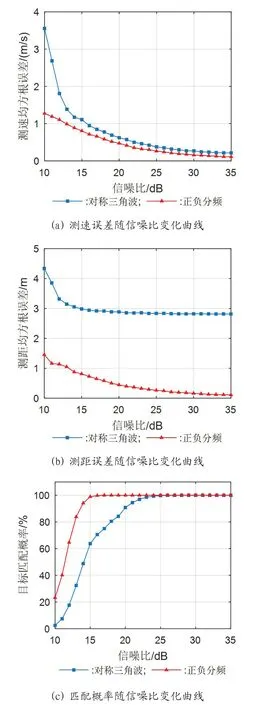
图5： 测量误差与匹配性能

由图5(a)可知，本文方法的测速性能整体优于对称三角波方法，尤其在10～15 dB低信噪比条件下更为明显。由图5(b)可知，本文方法的测距性能也是整体优于对称三角波方法。从图5(c)可以看出，因本文方法避免了仅依靠单一元素做匹配故使得匹配性能显著优于对称三角波方法，当信噪比达到15 dB 时，本文方法的匹配概率已经达到了99%，而对称三角波方法却需要在信噪比达到24 dB 时才能达到相同效果。可见，本文方法在测速与测距、目标匹配上的性能均优于对称三角波方法，抗噪性也表现得更好。

3.2 多目标场景

本小节以导弹群目标为例构造多目标场景。假定雷达波束宽度为4°，在某一时刻波门中心与雷达相距Rcen=150 km，当前探测波门内有5 个目标，它们的距离、径向速度、信噪比、波门中心相对角各不相同，但每种元素彼此又相差不大，目标详细设置信息见表2。

表2： 目标信息列表

使用正负分频信号进行仿真并脉压后结果如图6 所示。从图中可以看到，5 个目标的幅度和包络形状几乎一样，并且会因距离-多普勒耦合而导致目标发生交叉错位。在这种场景下用包络相关法或对称三角波方法进行目标匹配时，误配的概率会明显增大。

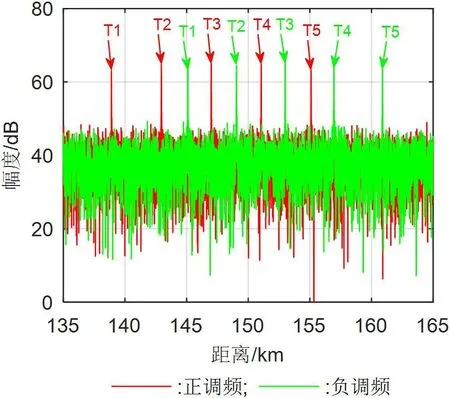
图6： 多目标脉压结果

在当前场景和参数设定下，CFAR 检测门限仍然取Thr=8.5 dB，匹配阈值η=0.8，使用对称三角波方法和本文方法各进行蒙特卡罗模拟仿真1000 次，经统计得到目标匹配与参数测量结果如表3 所示。

表3： 目标匹配与参数测量结果

通过对表3 分析可知，对称三角波方法对3 号目标的匹配概率最高，对其他4 个目标的匹配概率却低于3号目标一半的水平，这是因为3 号目标的信噪比最高且区别于其他目标，而其他4 个目标彼此均有1 个目标的信噪比与之相同。由此可见，仅用单个元素做匹配且多个目标间该元素又相同或相近时，目标误配的风险会明显增大。而本文方法综合了多个元素做匹配，故可以对5 个目标精确配准，匹配概率全部高达100%；此外，本文方法对5 个目标的速度与距离测量精度也是明显优于对称三角波方法，测量误差会因目标信噪比不同而有所差异，这与图5(a)的测速误差曲线、图5(b)的测距误差曲线基本一致。综合可知，本文方法对多目标场景的参数测量也表现得明显更优，为解决群目标的测速与测距问题提供新思路。

为近一步宏观考察本文方法对多目标匹配的准确度，基于同样的模拟场景，设置3 号目标脉压后的平均信噪比，其他目标的信噪比保持不变。在3 号目标每种信噪比下用对称三角波方法和本文方法各做蒙特卡罗模拟仿真1000 次，计算它匹配成功的概率曲线如图7 所示。

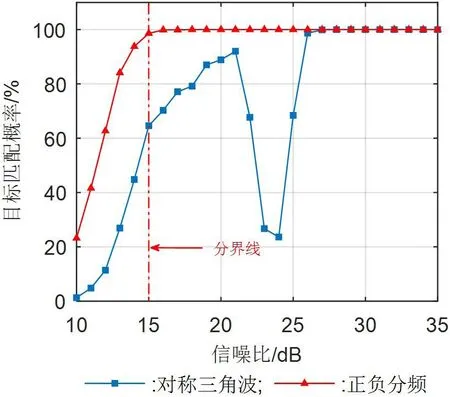
图7： 3 号目标匹配概率曲线

从图7 中可以看到，在当前多目标场景下，因对称三角波方法只用了幅度单个元素作匹配，故在3 号目标的信噪比与其他4 个目标的信噪比相近时（22～25 dB 的区间）匹配成功的概率会明显恶化。而本文提出的匹配方法不仅抗噪性更好，而且也不会因某个元素接近而发生恶化，即本文方法在多目标场景下有很好的鲁棒性。此外，结合图7 与图5(c)可以看到，无论是在单目标场景还是在多目标场景下，本文方法对目标的匹配性能几乎一致。当信噪比达到15 dB 时，目标匹配成功的概率会升至99%。可见SNR=15 dB 是一个重要的分界点，为保证本文方法的精准性，检测门限至少应设置为15 dB。

4 结束语

高精度测速与测距一直以来都是测控雷达系统的核心技术，也是实现目标稳定跟踪与测量的关键。根据线性调频信号时频耦合的特点，本文提出了一种基于正负分频信号的高精度测速与测距方法，无论是低速目标还是超高速目标，它既能测得目标的无模糊速度，又能保证速度与距离的测量精度；同时，本文还详细讨论了多目标的速度与距离测量方法，在获取特征元素构造匹配点集的基础上使用Clean 算法，大大减少了运算量，可以满足工程应用的实时性要求。本文方法不需要借助额外的波形，只用一个正负分频信号便可以实现多个目标的检测和高精度测速测距，在均衡雷达系统资源上有明显优势。