一种基于多目标约束下的UUV 航迹规划算法
韩喜红,丁天明,郑海林,刘 虎,鞠 拓
(浙江海洋大学 船舶与海运学院,浙江 舟山 316022)
0 引 言
无人水下航行器(unmanned underwater vehicle,UUV)凭借操纵灵活、可控性好、航行时间长等优势,被广泛应用于执行各种任务,如海洋环境数据采集、海洋资源勘探、通信中继、反潜警戒、水下侦察与监视、海洋工程和海底电缆检测等[1–3]。具有智能化、程度高和成本低的优点,可以代替人类执行水下危险任务。
UUV 因自身结构的限制,其大多采用“人在回路中”的控制方式[4],但是UUV 在水下航行中易受到风、浪和流等外界因素的影响,特别是在恶劣的海洋环境下,通信环境受到干扰,通信可靠性降低[5],造成通信中断。因此在复杂海洋环境下工作的UUV 必须要求具备一定的自主航行控制能力和自主校正能力,以适应航行过程中复杂变化的海洋环境[6]。另一方面精确的导航与定位技术是UUV 完成水下航行任务的关键因素,目前,UUV 的导航定位主要采用惯性导航系统[7],其在航行的过程中会产生位置误差,定位系统无法对自身进行准确定位,误差会随着时间累积,当误差积累到一定值时,将导致航行任务失败[8]。航迹规划技术是实现UUV 自主航行并完成水下任务的关键,其主要思想是在特定的环境中,规划出一条满足约束条件、目标最优的航迹。随着控制技术的发展,多约束条件航迹快速规划越来越重要,国内外学者对航迹规划问题进行了大量研究,并取得了一定成果。其中常用的方法有Dijkstra算法[9]、人工势场法[10]、模拟退火算法[11]、A*算法[12]等,本文主要从航迹规划、转向角、校正定位3 个方面建立模型,提出一种基于最小转向角搜索算法,并对算法的有效性对比讨论。
1 问题描述及模型的构建
1.1 问题描述
UUV 在水下执行任务时,可能会遇到恶劣的海洋环境,其通信受到影响,无法定位自身位置,定位误差累积增加,将会造成航行任务失败。航行区域中存在水平和垂直校正点,即用于校正定位误差的安全位置,且UUV 航迹转向点都在所给的校正点上,每次校正只能选取一个方向,需要在复杂海洋环境条件下找出一条满足以下条件的最优航迹:
1)UUV 的航迹长度尽可能的短;
2)经过校正点的次数尽可能的少;
3)UUV 在转弯时受到自身机动性能的限制,无法突然改变前进方向,其转向角应在一定的限制范围内,考虑到航迹的光滑度,要求转向角尽可能的小,UUV 允许的最大转向角为 ψmax。
1.2 UUV 模型构建
UUV 自起点A经 过n个校正点航行至终点B,经过校正点时进行误差校正,建立以起点A为圆心,r为半径的球形可航行区域,球形区域内的误差校正点为待选校正点。由误差校正和转向角度约束可知,求待选节点P0时 ,P点距离A点距离最近、转向角最小的点会被优先选中,经过校正点校正后该方向的误差校正为0,另一方向误差保持不变,寻找到第二个校正点P2时 ,以P2为 圆心r为半径划分球形可航行区域,在可航行区域内选择下一个校正点,重复选取过程直至终点B。选取过程如图1 所示。

图 1 校正点选取示意图Fig. 1 Correction point selection schematic
1.3 数学模型构建
已知UUV 的起点和终点,要使航迹长度尽可能短,满足约束条件下构建数学模型。本文设计一条经过若干校正点航迹长度最短的轨迹,使得在航经校正点处误差不断校正,从而能顺利达到终点。A(x0,y0,z0)表示起点坐标,Pi(xi,yi,zi) 表示第i个校正点坐标i=1,2,···n,终 点 坐 标 表 示 为B(xn+1,yn+1,zn+1) ,µ表 达 校正点的类型。

表 1 符号变量说明Tab. 1 Symbolic variable description
1)目标函数
要使航迹长度尽可能短,即目标函数为:

式中:d(0,1)为起点A到第一个校正点P1的距离;d(n,n+1)为 第n个 校正点Pn到 终点B的距离;d(i,i+1)为校正点Pi到校正点Pi+1的距离。

2)校正条件约束
第1 个约束条件是校正次数尽可能少:在起点A(x0,y0,z0) 时UUV 的垂直和水平误差均为0,即r0=0,s0=0 。UUV 前进 1 m,误差增加 δ个单位,航行器 从 第Pi−1个 校 正点 到Pi校 正 点 的 距 离 为di−1,i,产 生的 积 累 误 差 为 δdi−1,i,同 时 在 到 达 校 正 点Pi时 含 有i−1个未校正的原始误差 。
因此,校正前该点的垂直误差ri为 积累误差δdi−1,i与 原 始 误 差ri−1之 和,水平误差si为 积 累 误 差 δdi−1,i与原始误差si−1之 和,垂直误差ri和 水平误差si可以表示为:

当µ=1 时,进行垂直误差校正,α1和 α2为满足垂直误差校正的垂直和水平误差最大值,校正条件为:

校正后:

当 µ=0 时,进行水平误差校正,β1和 β2为满足水平误差校正的垂直和水平误差最大值,校正条件为:

校正后:

到达终点时垂直和水平误差均满足以下条件:

由式(4)~ 式(9)可知校正误差随着航行距离增加,因此,可以把误差校正约束转化为待选点间距离约束。
3)转向角条件约束


图 2 转向角约束示意图Fig. 2 Diagram of steering angle constraint


考虑到UUV 的操纵性能,当转向角大于90°时,操纵及为困难,且在海底存在暗流的复杂情况下,控制过弯的失误率明显增加,航行过程中还要减少航迹折返的情况,因此在航迹规划时各校正点处转向角越小的点应该优先考虑,在满足校正条件和偏转角约束下建立目标函数。
1.4 算法步骤及流程
步骤1以A 为起点,求待选点到A 点的距离d(A,Pi)。
条件1:判断待选点是否定在以r为半径的可行域内d(A,Pi) 步骤2求当前点到待选点偏向夹角 ψi,在可行域内选取 ψi最小的点,进行水平或垂直校正,作为下次迭代的起点。 步骤3从当前点出发到终点B 的航迹距离是否满足条件3,如果满足,则输出最终航迹,停止迭代,如若不能到达B 点,迭代次数加 1,返回步骤 1。 具体算法流程如图3 所示。 图 3 航迹规划算法流程Fig. 3 Route planning algorithm flow 根据上述模型和算法,其参数分别设置为 α1=25 ,α2=15 ,β1= 20,β2= 25 ,θ = 30 ,δ = 0.001 ,起点坐标A(0,50000,5000), 终点坐标B(10000,59652.34,5022),校正点数量共612 个,坐标参数如表2 所示。 表 2 部分校正点坐标Tab. 2 Correction point coordinates 基于表2 数据,针对上述2 种约束条件,调整半径10000~20000 m,利用 Matlab 数值模拟仿真,可以得出不同调整半径r对应的校正点次数和航迹长度。由图4 可知,基于距离约束时,调整半径小于11000 m得不到航迹规划结果,当调整半径r=14000 m 时航迹长度最短,调整半径r=18000 m 时校正点次数最少。基于距离和转向角约束情况下,当r=14000 m 时校正次数为8,航迹长度为106350 m,此后再增加调整半径的值,路径长度不再减少,校正次数不变,比基于单一距离约束下的算法提前达到最优。 图 4 不同调整半径对比图Fig. 4 Comparison of different adjusting radius 基于航迹长度约束条件仿真实验数据对比,结果见表3。可知,当调整半径r小于10000 m 时,由于球形可航行区域内的点减少,找不到满足校正条件的待选点,无法得到仿真结果。当调整半径r=14000 m时,航迹长度最短为128909 m,总转向角度最小为523.46。当调整半径r=18000 m 时,校正点最少为11 次,与r=14000 m 相比,校正次数减少了2 次,但航迹长度增加1206 m,为了直观呈现路径平滑度,做出二维航迹平面图。 表 3 不同调整半径对比结果Tab. 3 Comparison results of different adjustment radius 如图5 所示,在只考虑航迹长度约束的算法下,航迹路径上的校正点会出现从起点到终点方向的折回、相邻、平行的现象。当r=12000 m 时,航迹平面图出现6 次折回和 1 次相邻的现象,校正点次数多达18 次,航迹长度为143331 m,第5 个校正点偏向角最大为121.80°;当r=13000 m 时,航迹平面图出现3 次折回、1 次平行和1 次相邻的现象,校正点次数为16 次,航迹长度为144041 m,第13 个校正点偏向角最小为4.52°;当r=14000 m 时,航迹平面图出现1 次折回和1 次相邻现象;当r=18000 m 时,航迹平面图出现2 次折回现象,航迹最靠近AB 直线方向,该算法达到最优,此后再增加调整半径r的值,航迹长度和校正次数不在减少。 图 5 不同调整半径的航迹规划平面图Fig. 5 Plane diagram of route planning with different adjustment radius 在航迹长度约束的基础上增加转向角约束条件对比数据分析,其具体结果见表4。 由表4 可知,调整半径r增大时,航迹长度变短,校正点次数减少,总转向角度变小。当半径r达到14000 m 时,再次增加调整半径r的大小,其航迹长度、校正点个数和总转向角保持不变,说明算法达到最优值,为了直观呈现路径平滑度,做出二维航迹平面图。 表 4 不同调整半径对比结果Tab. 4 Comparison results of different adjustment radius 如图6 所示,当r=11000 m 时,校正点次数多达13次,所得的航迹长度为115848 m,总转向角度为349.24°,第10 个校正点转向角最大,最大值为64.34°;当r=12000 m 时,校正点次数为10 次,所得的航迹长度为111306 m, 总转向角度为202.87°,与r=11000 m 相比,校正点减少3 次,总转向角减少146.37°,当r=13000 m时 ,经过9 个校正点,所得的航迹长度为111926 m,与r=12000 m 时的航迹对比,虽然校正次数减少1 次, 但航迹距离增加620 m, 当r=14000 m 时,经过的校正点8 个,所得的航迹长度为106350 m,第7 个校正点转向角最小,最小值为5.22°,总转向角度变小为120.66°,UUV 航行轨迹为A-521-64-80-170-278-369-214-397-B,航迹方向最接近直线AB,得到最优解。 图 6 不同调整半径的航迹规划图Fig. 6 Path planning with different adjustment radius 结果表明,在合理范围调整半径r,能够有效缩短航迹长度,减少校正次数和总转向角度。如表5 所示,对比2 种方法,当考虑转向角约束条件时,校正次数为8 次,优于单一路径最短规划方法的11 次,路径长为106350 m,相较于单一路径最短规划方法的130115 m,其规划航迹长度减少了23765 m,航迹平滑没有折回、比邻、平行的情况,满足UUV 在水下复杂环境中的航迹规划,图7 为2 种约束条件下对应的最优三维航迹图。 表 5 两种方法对比Tab. 5 Comparison of two methods 图 7 不同约束下最优三维空间航迹图Fig. 7 Optimal three-dimensional space trajectory under different constraints 本文围绕UUV 在复杂海洋环境中航行时误差校正问题,建立单目标函数,根据约束条件的不同,在基于单一航迹长度最短规划基础上,提出考虑转向角约束的最小转向角航迹规划算法,通过对比可以发现,考虑转向角约束条件时,航迹长度明显缩短,校正次数减少,路径光滑,满足航行要求。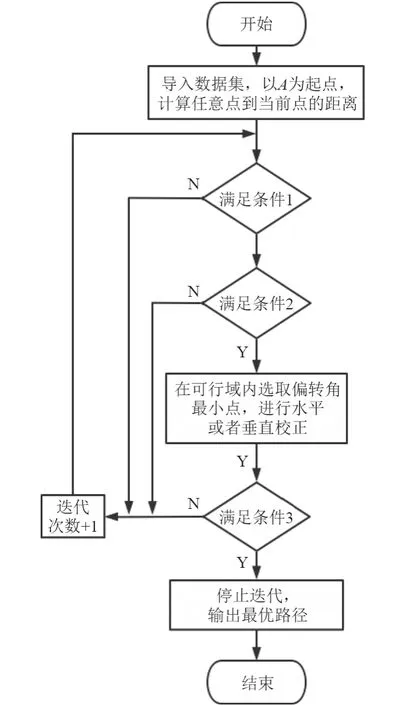
2 仿真实验


2.1 基于航迹长度约束数据分析


2.2 基于转向角约束数据分析




3 结 语

