不同客流下的城市轨道交通乘客进站时间研究

蒋远伟 向红艳

(重庆交通大学交通运输学院 重庆 400074)

0 引 言

城市道路交通拥堵,汽车尾气污染、燃料能源消耗等问题显著,而城市轨道交通具有便捷、舒适、准点、环保、节能等诸多优点,因此成为我国大城市公共交通的主骨架,对解决城市交通拥堵具有重要意义.

国内学者十分关注城市轨道交通客流和乘客行为的研究.关菲菲等[1]分析了重庆轨道交通客流量数据并总结其客流量分布特征.郭平等[2-4]对城市轨道交通网络客流特征和预测方法进行了研究.徐瑞华等[5]通过分析城市轨道交通列车运行延误对乘客出行方式选择的影响,提出了换乘车站大客流预警方法.李曼等[6]通过分析轨道交通车站内不同环境下客流等因素之间的关联关系,建立了站台层客流仿真模型,并提出了控制站台客流的措施.柳泽原等[7]基于Anylogic仿真软件研究了车站闸机口通行能力.孙世炜等[8]基于地铁站内不同车站设备处的行人速度变化规律,建立了乘客密度与速度的关系模型.甘金荣等[9]对城市轨道交通乘客等待时间进行了建模研究.

上述研究表明:城市轨道交通客流量是变化的,对轨道交通车站的服务水平有显著影响.文中究了不同客流状态下的轨道车站服务设施的服务时间,建立乘客进站过程时间模型和进站总时间模型,为城市轨道车站的客流管理、预警、疏散提供借鉴.

1 进站时间

乘客从到达轨道车站进站口开始,到进入车厢的全过程服务时间.进站时间可分为乘客行程时间、设备服务时间、候车上车时间三部分.①乘客行程时间是指乘客步行经过通道、楼梯等的行走时间;②设备服务时间是指乘客使用站内的购票机、安检机、闸机等消耗的时间;③候车上车时间是指乘客在站台层等候轨道车辆到达以及进入车厢的时间.进站时间是乘客交通出行时间的一部分,反映了车站服务能力和乘客出行特征.

乘客总进站时间为

T=T1+T2+T3

(1)

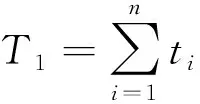
(2)

T2=Twk+Tt

(3)

T3=Twt+Tb

(4)

式中:T为乘客进站时间(总时间);T1为设备服务时间;T2为乘客行程时间;T3为候车上车时间;ti为设备i的服务时间;Twk为乘客站内走行时间;Tt为乘客换层时间;Twt为乘客候车时间;Tb为乘客上车时间.

2 建立模型

2.1 设备服务时间模型

运用排队论的方法来构建设备服务时间模型.其中乘客购票、安检、过闸机、乘坐自动扶梯和垂直升降电梯的过程均可以看作为M/M/C的排队系统.虽然车站内服务设备具有容量限制,但是当达到容量限制后乘客不会离开且必须通过排队才能进入该系统,故可看作无容量限制的排队模型.设轨道车站的客流量为q人/min,即车站乘客到达率λ为q,车站各设备服务效率为μ,设备数量为c,在排队论模型中,当乘客到达率大于服务率时便会出现无限排队的现象,因此需要限定服务强度ρ小于1,为

(5)

(6)

(7)

式中:q为车站客流量;ti为乘客在系统中的逗留时间;ρ为系统的服务强度;P0为服务设备空闲概率.

2.2 乘客行程时间模型

采用BPR(路阻函数)模型建立乘客站内走行速度与走行时间的关系模型.研究表明乘客在换乘通道的走行速度大于上下楼梯的走行速度,上楼梯的速度较慢于下楼梯的速度[10].建立轨道车站内乘客走行速度与密度的模型时需要考虑乘客在不同环境下的走行速度的差异性.文中根据实测数据拟合结果,得出车站内乘客步行速度与密度呈幂函数关系,并得到乘客使用楼梯耗费时间计算公式为[11]

(8)

式中:Ls为楼梯的长度;Ss为楼梯面积;X为乘客人数;α、β、γ为估计参数,用最小二乘法标定.

乘客站内走行时间是指乘客进站后在站厅、站台以及通道等区域的步行时间.乘客站内走行时间与走行距离和走行速度有关.其中,走行速度主要受到客流量的影响.当客流量时较小,乘客密度较小,乘客走行速度较高;当客流量变大,乘客之间的相互影响随之增加,乘客走行速度便会减少.

2.3 乘客候车和上车时间模型

2.3.1上车时间计算

乘客上车时间是指列车到站停稳,开启车门后,乘客从站台到车厢内所需要的时间.乘客上车时间主要受上车乘客数量、车门宽度等影响,其主要影响因素为上车乘客人数,通过拟合实测数据,得到上车人数和上车时间的幂函数关系,上车时间为

(9)

式中:Tb为乘客上车时间;q为客流量;m为发车间隔;n为轨道车辆车门数量;ω和θ为参数,用最小二乘法标定.

2.3.2候车时间计算

根据运营计划,在一定的时间周期内,轨道车辆发车时间间隔是固定的,车辆达到服从均匀分布,乘客到达服从泊松分布.根据城市轨道交通列车的运行时刻表,其发车间隔在一定周期内固定不变,设列车的发车间隔为m(单位:min),前一辆列车离开时间为t0,乘客到达时间为tar,则乘客候车时间为

(10)

(11)

式中:t为乘客候车的时间;f(x)为概率密度;Twt为乘客平均候车时间.

2.4 乘客进站总时间

根据式(1)～式(11),计算乘客进站总时间,得.

(12)

式中:第一个中括号为设备服务时间;第二个中括号为乘客行程时间;剩余为乘客候车和上车时间.

2.5 模型对比

由于车站不同客流下的实际进站时间获取难度较大,采用行人微观仿真软件进行模型对比.构建仿真模拟场景见图1,通过输入不同客流量得到进站时间散点图,进行曲线拟合见图2.

图1 模拟仿真场景效果图

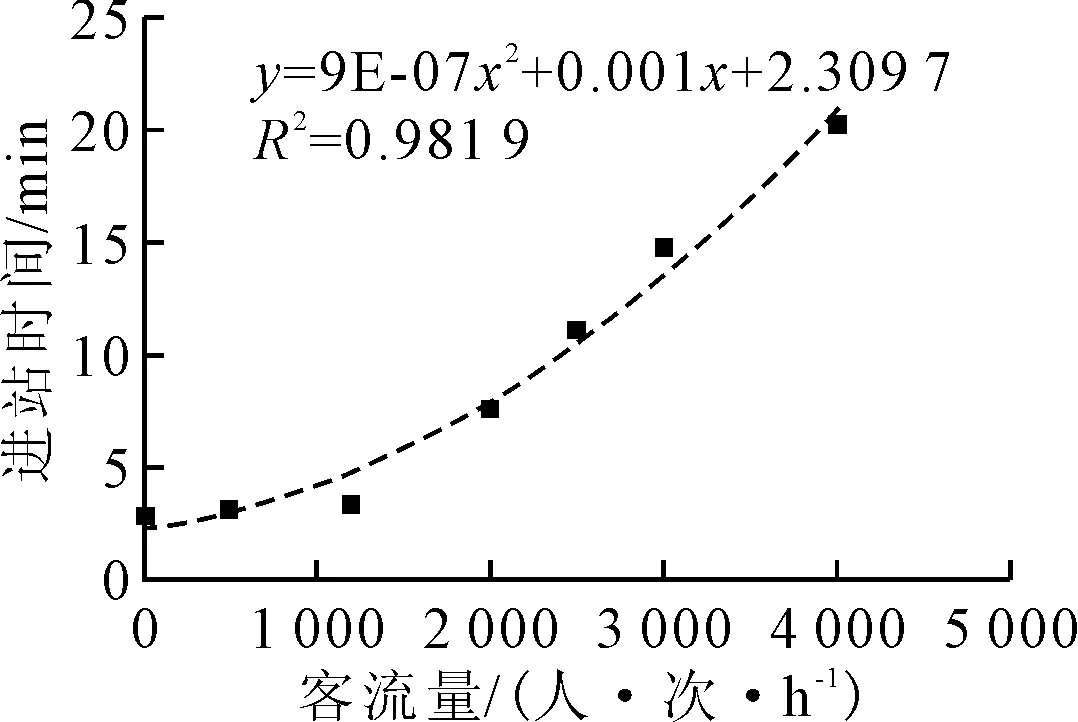
图2 仿真模型进站时间曲线拟合

3 模型应用

以重庆市城市轨道交通四公里站为例,根据现状设施及客流量,分别对该车站的站台层和站厅层的面积、设备数量、客流量进行了测量和统计,原始数据见表1.

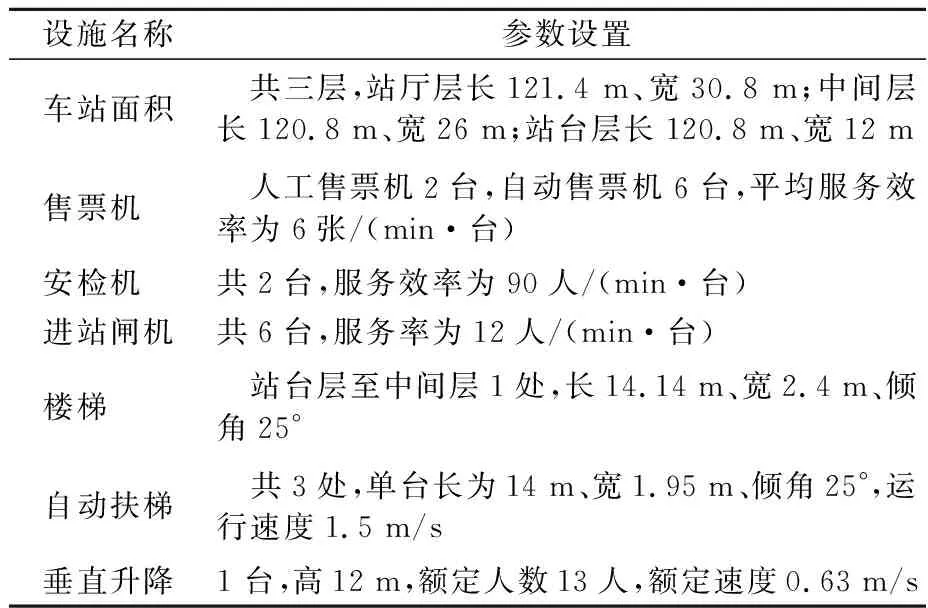
表1 重庆轨道交通四公里车站基础数据

调查该车站楼梯处和走行通道处的乘客密度与乘客速度数据,得到两者关系见图3.

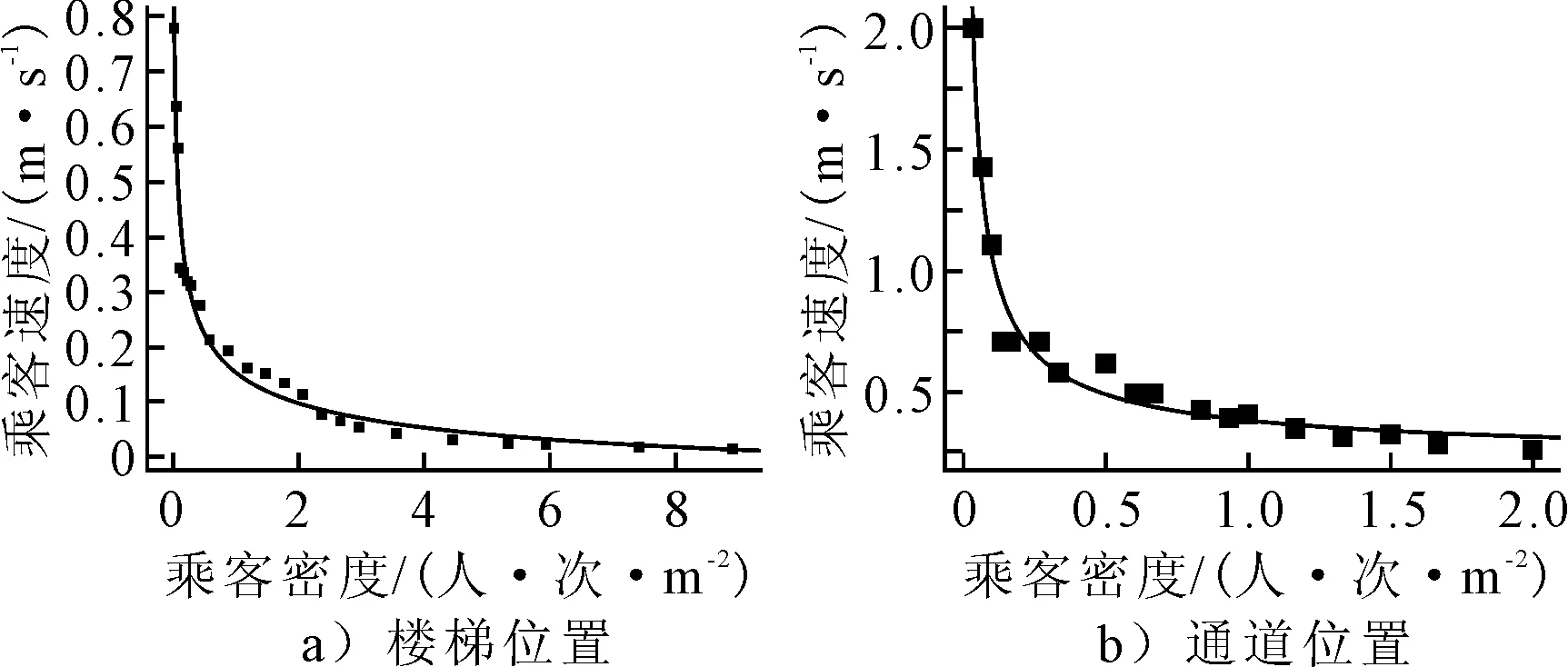
图3 通道位置乘客密度-速度曲线

计算乘客在楼梯处和通道处速度与密度函数关系,标定公式中的参数,见表2.

表2 乘客速度-密度关系函数

根据式(7)～式(9)和式(11),计算不同客流状态下各流程耗时,结果见图4.

图4 各流程耗费时间

由图4a)～d)可知,不同客流量条件下,设备服务时间不一样.由图4a)可知:当客流量小于2 000人·次/h,乘客购票耗费时间较短,变化率较低;当客流量为2 000人·次/h～3 000人·次/h,乘客购票耗费时间增长率显著增大;当客流量大于3 000人·次/h,客流量突变,购票处拥挤加剧,此处为服务时间拐点.图4b)～c)增长趋势同图4a),均为当客流量较小时,耗费时间增长率较小,当客流量增大到临界值时,增长率变大,耗费时间突变.由图4d)可知:客流量小于4 300人·次/h,设备服务时间基本保持稳定,当客流量不断接近4 300人·次/h,设备服务时间突变,其主要原因在于乘客到达率到达了闸机服务能力的临界值.不同设备的服务时间突变临界点不一样,且具有累加效应.

由图4g)可知:当客流量较小时,行程时间也较小,但增长较高;当客流量逐渐增大时,乘客行程时间趋于稳定,增长率较低.由图4h)可知:随着客流量的不断增加,候车上车时间增加,增长率较稳定.根据式(12),计算不同客流量下乘客进站总时间,并通过仿真曲线拟合公式计算出不同客流下的仿真总时间和变化关系见图5～6.由图5～6可知:仿真曲线变化较为平缓,数学模型在设备通行能力阈值客流发生突变,可以较好的反应设备“短板”效应,同时模型可以较好的反应出客流密度对乘客速度的影响.

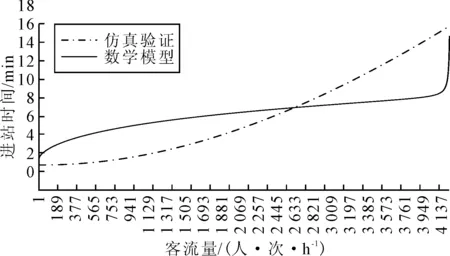
图5 数学模型与仿真模型对比

由图6可知:乘客进站时间随着乘客进站客流的增加而增加,且各阶段的变化程度有所差异.当小客流时,即客流小于1 500人/h,乘客进站时间增长率较大,其主要原因是乘客站内走行速度变化受乘客密度影响较大,在乘客密度为0～0.4人·次/m2时,乘客走行速度由2减至0.6 m/s;当中客流时,即客流为1 500～4 500人/h,乘客进站时间随着客流的增加变化较为缓慢;当大客流时,即客流到达临界值4 500人/h,乘客进站时间突增,其主要原因是受到闸机组服务效率的影响,此时乘客到达率逼近闸机组服务效率,闸机处拥堵严重.

图6 客流量-乘客总时间曲线

根据案例车站全天进站AFC数据,计算出全天各时段各流程耗时和总进站时间,见图7～8.结果表明:乘客行程时间占比最大,平均时间约为4 min,占进站时间比例为50.33%其主要原因为站内走行距离较长,且乘客行程时间受客流量影响较大.其次是候车上车时间,平均时间约为3 min,占比40.85%,其值变化不大.其余设备服务平均时间小于1 min,占比8.82%.

图7 进站各流程耗时曲线

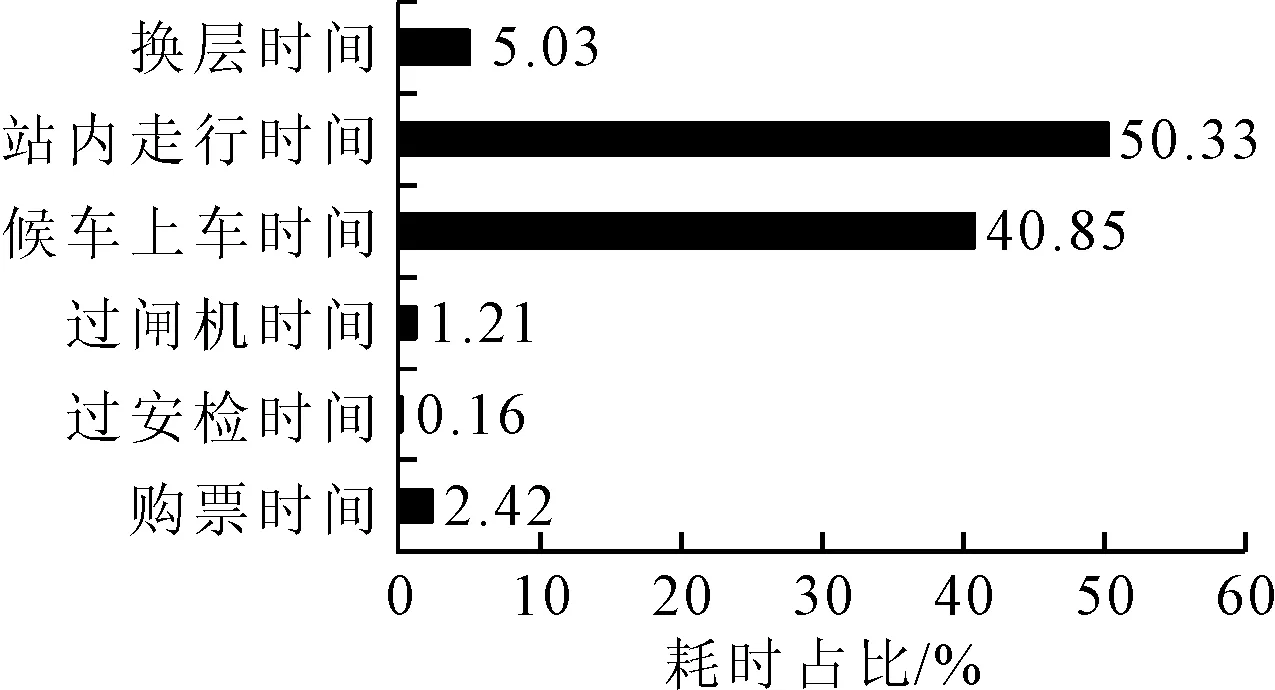
图8 各流程耗时占比

根据全天24 h客流量,计算24 h进站时间分布,见图9.结果表明,06:00—08:00时间段,客流量由0增长至最高峰,乘客进站时间随着客流的增加逐渐增加,08:00点进站时间达到最大值,约为10 min;08:00—18:00时间段,乘客进站时间较稳定,约为8.5 min;18:00以后,随着乘客数量的减少进站时间逐渐减少.说明该车站客流量基本饱和,全天客流较为均衡,进站时间较长.

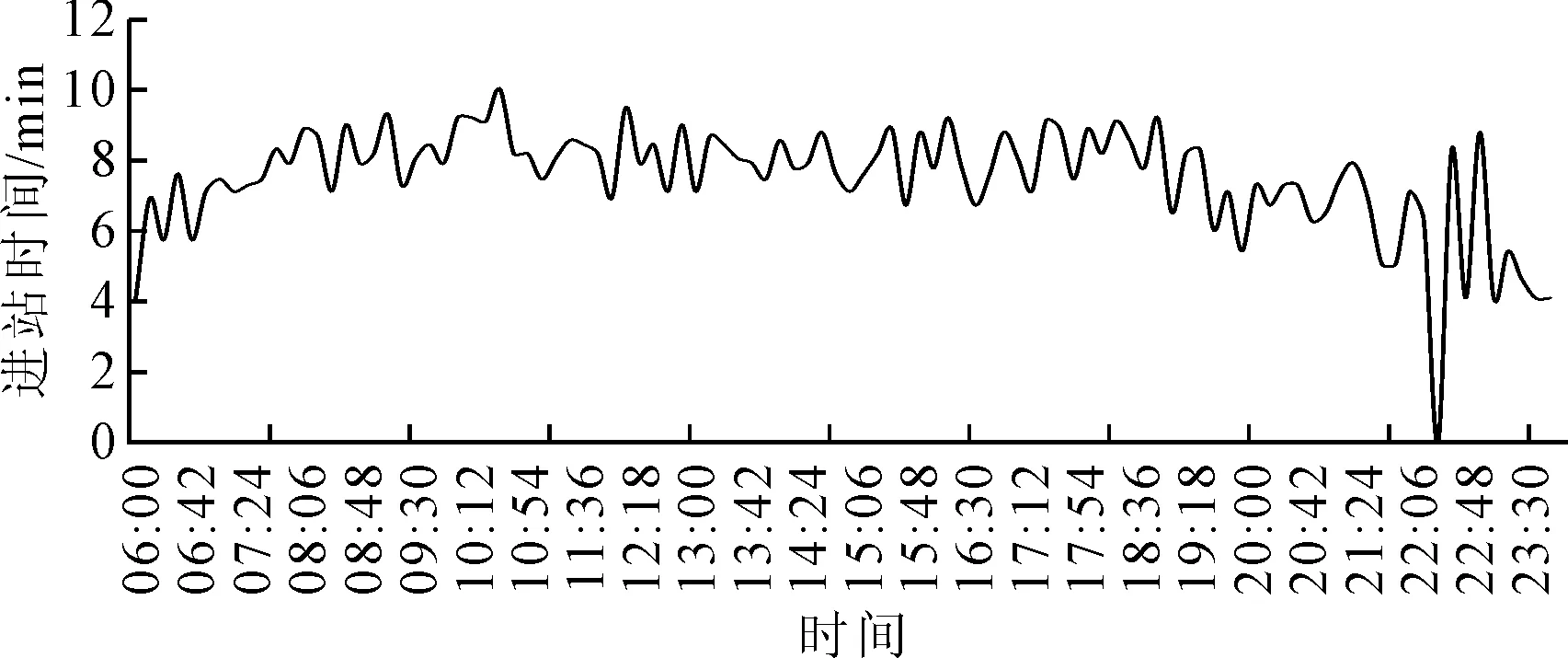
图9 24 h进站时间曲线

4 结 论

1) 客流量对乘客行程时间的影响最大,乘客站内行程时间占进站总时间的50%以上.

2) 小客流量状态下,乘客进站时间较少,但变化率较高.

3) 进站时间的突变点为客流量饱和值与设备服务能力临界值叠加后的结果,进站时间的突变容易引起车站拥挤加剧.

4) 优化乘客步行空间,科学规划各服务设备的数量,提高“短板”设备服务的效率可有效提高车站整体服务效率.