基于碰撞检测的空间超大规模航天器拼接曲面优化

付瑶，康国华，周绍辉，武俊峰，华寅淼，吴佳奇，胡苗苗

（1.南京航空航天大学 航天学院，江苏 南京 211101；2.上海航天空间技术有限公司，上海 201109）

0 引言

天基太空望远镜在天文观测、空间环境监测等领域都具有重要的应用价值，其主镜尺寸对成像效果具有重要影响［1-3］。对于单镜面的天基太空望远镜而言，镜片尺寸一直以来受限于单次发射运载对航天器体积和质量的约束，而拼接技术可以有效解决该问题。目前拼接技术已经广泛应用于许多地基太空望远镜的设计中，如凯克望远镜（Keck）、霍比-埃伯利望远镜（Hobby-Eberly Telescope，HET）、加纳利大型望远镜（Gran Telescope Canarias，GTC）、南非大望远镜（South African Large Telescope，SA-LT）等［4］。拼接技术在天基太空望远镜中也具有较大的应用价值，如目前国际上最大口径的天基太空望远镜——詹姆斯·韦伯空间望远镜（James Webb Space Telescope，JWST），其等效口径为6.5 m。在太空要实现上述技术将面对模块化航天器在轨拼接优化问题。

模块化航天器可以分批入轨、在轨拼接和重构，从而摆脱单次发射运载对航天器体积和质量的约束，有效地降低成本，因此近年成为研究热点［5-11］。鉴于上述优势，长期受限于单个镜片大小约束的天基光学望远镜、需大规模面积拼接的空间电站等下一代空间超大型机构都同样采取了模块化航天器设计［12-13］。如英国萨里大学和美国加州理工学院联合开展的可重构空间望远镜的自主组装（Autonomous Assembly of a Reconfigurable Space Telescope，AAREST）计划，研究若干个搭载光学载荷的立方星在轨组装、重构、成像的相关技术［14］。

太空光学孔径自组装（Optical Aperture Selfssembly in Space，OASIS）项目通过小模块自主交会对接后装配成孔径大于5 m 的光学望远镜［15-16］；蜂巢（Hive）项目将模块在轨组装成立方体或蜂巢的形状并执行模块翻转、换位、跳跃等［17］；卫星在轨服务智能建造模块（Intelligent Building Blocks for On-Orbit Satellite Servicing，IBOSS）项目研究将立方体形状的智能模块在轨装配成为可重构航天器，目前正在进行在轨演示与测试［18］。

空间超大规模模块化航天器的“拼接-变构-重构”规划是任务的基础，但现有研究一般假设目标构型固定不变，对如何变构还缺乏深入研究。如未考虑对接机构及载荷尺寸所带来的拼接间隙限制，但实际上间隙约束对模块化航天器的构型规模、变构范围和重构顺序都将有很大影响。

本文以大型空间望远镜为模块航天器拼接的应用场景，以正六棱柱模块为航天器单位构型进行拼接。根据正六边形可在平面上满铺的特性，提出了一种映射平面的不闭合的“蜂巢”构型作为空间望远镜目标曲面，即蜂巢中每个正六边形的面对应为一个模块卫星的顶面，并针对该模型在相邻模块的间隙约束的条件下，获得模块布局的最优解以及构型相关参数的求解，如图1 所示。

图1 自然界球冠曲面Fig.1 Spherical crown surface in nature

1 基于“球冠-平面”映射的拼接曲面建模

1.1 基于“球冠-平面”的拼接映射

分批入轨的模块航天器如何拼接成所需的成像曲面，是构成空间望远镜的关键。模块拼接成曲面，一般有2 种方法：①所有模块先拼接成整体，再通过模块间的对接机构调整至目标曲面；② 所有模块按预先规划的路线直接拼成所需的曲面。很明显，方法①虽有利于模块拼接，但鉴于模块间存在多个对接机构的强约束，如中心模块需要与周围6 个模块进行对接，因此在进行整体变形时，将要逐个规划每个对接机构的运动，过程复杂且耗时。本文将采取第2 种方法，但需要解决初始模块位姿和目标模块位姿之间的规划问题。

考虑到空间望远镜成像需求，模块卫星构成的镜面曲面中心对称性越好，则其成像效果越好。因此所有模块将会形成以某个模块为中心的球冠曲面。本文提出了一种“球冠-平面”映射法，将对称目标曲面与辅助平面的模块进行一一映射，形成排布规划。

如图2 所示，曲面A为模块卫星所携带镜片需要构成的目标曲面，曲面中心点为O，曲面由模块卫星所携带的正六边形镜片确定：每个镜面的中心点Pi（i表示模块编号，i=1，2，3，…）为镜面与曲面的外切点。曲面的中心O点与Pi连线在曲面的外切平面B上有映射点，点是Pi所在六边形镜面在平面B上投影六边形镜面的中心。基于上述对应关系，将模块卫星的曲面拼接，转换成平面拼接；在平面B上布局后，将模块移动至曲面对应位置再进行对接，即可得到目标曲面。

图2 平面辅助映射法Fig.2 Schematic diagram of the plane-assisted mapping method

1.2 拼接曲面模型的建立

为保证整体的中心对称性，将所有模块按圈层排布，如图3 所示。假设共s个模块，中心模块为第0 层，从中心模块向外依次为第0 层、第1 层、第2 层、…、第n层，则n与s之间的对应关系为

图3 模块编号顺序及间距Fig.3 Schematic diagram of numbering and arrangement of the modules and vertices

以中心模块正右方的模块为每层的第1 个，逆时针方向依次为第1 个、第2 个、…、第6n个。对于每个模块而言，最右侧为第1 个顶点，逆时针方向依次为顶点1、顶点2、…、顶点6。

设假想平面B上，第i层与第i+1 层相邻两个模块之间的距离为bi，其中i=1，2，…，n-1。所有模块的边长均为a，目标曲面中所有模块顶面六边形镜面拼接后拟合成的球冠的半径为r，即曲面的曲率半径为r。这里设目标曲面中所有模块顶面六边形对应的球冠球心坐标为（0，0，r），球冠表面方程为x2+y2+（z-r）2=r2。设中心模块正六边形中心的位置坐标为（0，0，0），中心模块上表面六边形的六个顶点坐标分别为

假设在z=0 平面上绕中心有s个模块排布成n层，相邻两层模块的相邻两条边之间的距离分别为b0，b1，…，bn-1，则第1 层模块的每个正六边形的中心点坐标分别为

依此类推，平面上位于第i层的第j个模块的中心点坐标的值为

旋转角为

因此对于每个正六边形的中心点Pi到其六个顶点的矢量为

1.3 基于包围盒的模块碰撞检测

碰撞检测（Collide Detection，CD）用于判断两个或多个物体占据的三维区域在同一时间是否相交，在虚拟现实［19］、3D 游戏［20］、轨迹规划［21-22］、多体机器人［23-24］、星座构型保持［25］等领域中都具有广泛的应用。对于组合体航天器而言，至关重要的是判断变构过程中或变构结束后航天器的各独立模块之间是否发生碰撞。

目前研究较为成熟且应用较为广泛的CD 算法主要为层次包围盒算法等。常见的包围盒有包围球、轴向包围盒AABB、方向包围盒OBB 等。其中包围球和AABB 包围盒紧密性较差，而OBB 包围盒的计算较为复杂。

因为本文中模块的正六棱柱结构较为规则，同时考虑到算法的效率，本文采用改进后的层次包围盒方法进行CD。在层次包围盒算法中，针对给定物体E，E中的所有基本几何元素组成的集合为S，则定义层次包围盒树（Hierarchical Bounding Volume Tree，HBVT）［26］：①树中的每个节点v与S的一个子集Sv（Sv⊆S）相对应；② 节点v的数据值为集合Sv的包围盒b（Sv）；③根节点对应于全集S，其数据集为全集S的包围盒b（S）；④ 树中的每个叶节点指向的是物体的基本几何元素。

在层次包围盒算法中，图元被划分为不相交的层次结构。但对于本文的正六棱柱模块而言，直接划分为如图4 所示的3 个相交的长方体形状的AABB 包围盒，该方法保证了包围盒与模块形状完全相合，相较于传统的包围球算法，AABB 包围盒算法提高了紧密性，且算法的复杂度小于OBB 包围盒算法。

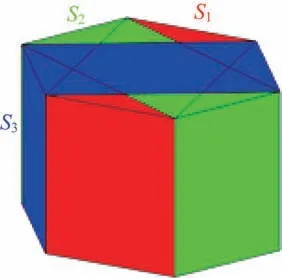
图4 层次包围盒分割Fig.4 Diagram of hierarchical bounding box segmentation

对于组合体中任意相邻的两个模块A和B，分别对A的3 个图元和B的3 个图元进行CD，即可判断A、B之间是否发生碰撞。

2 基于碰撞检测的拼接曲面优化

2.1 基于“球冠-平面”的拼接映射

在上述“球冠-平面”辅助映射法中，模块顶面正六边形边长a决定模块的尺寸；模块数目s决定拼接曲面的规模；目标曲面的曲率半径r决定拼接曲面的弯曲程度；假想平面中模块间距bi决定拼接曲面中模块之间的距离。通过改变模块数目s、目标曲面的曲率半径r、假想平面中模块间距bi的值即可得到不同的拼接曲面。但还需要考虑拼接的可行性：当前曲面中是否会发生模块之间的碰撞问题。考虑到模块之间是否发生碰撞的问题，在实际任务中，组合体航天器的拼接曲面存在以下2 个优化问题：

①当模块顶面正六边形边长a、模块数目s一定而拼接曲面的曲率半径r和假想平面中模块间距bi的值改变时，拼接曲面的曲率半径r越小，曲面的弯曲程度越大，如图5 所示。当曲面弯曲到一定程度时，无论如何改变假想平面中模块间距的值都必然会发生模块间的碰撞，因此存在拼接曲面的曲率半径r的最小值求解问题。

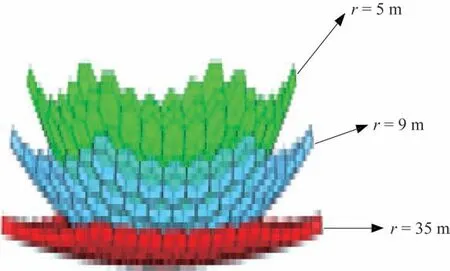
图5 不同弯曲程度的拼接曲面Fig.5 Spliced surfaces of different degrees of bending

② 当模块顶面正六边形边长a、模块数目s和目标曲面的曲率半径r固定而假想平面中模块间距bi的值改变时，拼接曲面的可行解有多个，模块间距有疏有密，如图6 所示。在实际任务中，模块间距离越短，则星间测量及通信的能量消耗越少，因而存在最紧密的拼接曲面的求解问题。在最紧密的拼接曲面中，模块顶面边界的最远距离l将达到最小值，即曲面的口径最小。

图6 紧密/稀疏曲面Fig.6 Compact/sparse surfaces

2.2 优化算法适应度函数的构建

以上两个问题中均包含一个共同的变量：假想平面中模块间距bi，在其他变量的值一定时，通过改变bi的值即可得到满足要求的拼接曲面以及相关变量的取值范围。但s取值会影响bi的个数，如s取91时，曲面中模块排列为6 层，本问题中的自变量包括b0、b1、b2、b3、b4共5 个；而当s取127 时，曲面共7 层，本问题中的自变量包括b0、b1、b2、b3、b4、b5共6 个，因此在处理不同的优化问题时自变量的个数不确定。为了设计不失一般性的优化算法，建立bi与模块所在层数i之间的函数关系，将bi与i之间的关系用一个二次函数进行近似的拟合，即设bi=a0+a1i+a2i2，此时对于上一章中提到的曲率半径最小值求解问题而言，无论模块数目有多少，自变量均为a0、a1、a2、r；对于最紧密拼接曲面求解问题而言，无论模块数目有多少，自变量均为a0、a1、a2。

上述两个优化问题本质是含非线性约束条件的非线性优化问题，本文采用遗传算法进行求解，在求曲面曲率变化范围的问题中需要求得曲率半径r的最小值；在求最优曲面的问题中需要求得曲面口径l的最小值。约束条件为所有模块之间均不发生碰撞，引入一个参数c对模块之间是否发生碰撞进行量化：

基于此，分别构造两个优化问题的遗传算法适应度函数：①对于求曲率半径变化范围的问题，

② 对于求最优曲面的问题，

式中：p为大于1 的常数。

可以保证在遗传算法迭代过程中适应度函数f1和f2始终为非负数，且适应度函数f1和f2取得最大值时，对应的曲率半径r和曲面口径l分别取得最小值。优化变量与指标见表1。优化算法流程如图7所示。

图7 优化算法流程Fig.7 Flow chart of the optimization algorithm

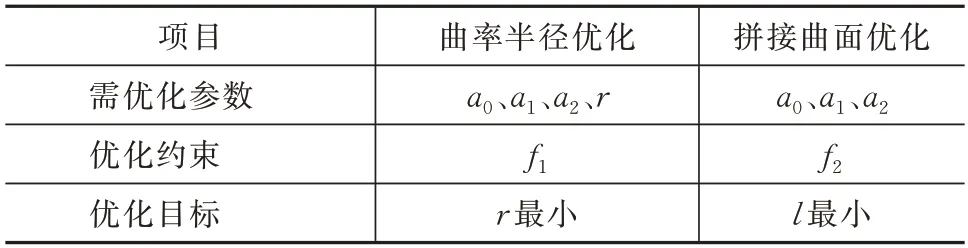
表1 2 个优化问题的变量与优化指标Tab.1 Variables and optimization indexes of two optimization problems

3 仿真验证和分析

3.1 平面辅助映射法的仿真与分析

设置所有模块正六边形的边长a=0.3 m，拼接曲面的曲率半径r=35 m，模块总数目为127，绕中心围成7 层。在辅助平面上a0=a1=a2=0，即b=0时所有模块顶面刚好将辅助平面上其所在的区域满铺，因此为保证拼接曲面中所有模块之间均不发生碰撞，至少需要保证bi＞0（i=1，2，3，4，5，6）。简单尝试后设置a0=0.10，a1=0.01，a2=0.01，即bi=0.10+0.01i+0.01i2。

由以上方法得到的127 个模块顶面的拼接曲面可以拟合为一个半径r=35 m 的球冠表面，且所有模块顶面所在平面的法向量均指向球心，顶面中心点均位于球冠表面上。对上述拼接曲面中的所有模块进行CD，若模块之间发生碰撞，则发生碰撞的两个模块显示为红色；若不发生碰撞，则显示为蓝色，结果如图8 所示。上述仿真结果表明，本文提出的六棱柱分割CD 方法有效。

图8 碰撞检测算法验证Fig.8 Verification of the collision detection algorithm

3.2 拼接曲面优化的仿真与分析

使用遗传算法对最优拼接曲面、曲率半径可变范围这两个问题进行求解。

3.2.1 曲率半径最小值求解

设置所有模块正六边形的边长a=0.3 m，模块总数目为127，绕中心围成7 层。使用遗传算法求解获得了曲率半径的最小值为23.44 m，此时对应的参数取值分别为a0=0.1，a1=0.000 027，a2=0.004 7。因此，曲率半径的可变范围为［23.44 m，∞］，在该范围内均可找到能使得所有模块均不发生碰撞的拼接曲面。因为遗传算法所得结果具有可能陷入局部最优的局限性，为了避免这种情况，将遗传算法重复运行50 次，所得结果如图9 所示。

图9 运行50 次遗传算法后的曲率半径结果Fig.9 Results of rafter 50 iterations by the genetic algorithm

50 次结果的均值为23.44 m，且最后都可以稳定收敛到最优值处。从统计结果来看，优化算法所得到的曲率半径最小值结果稳定有效。

3.2.2 最密拼接曲面的求解

设置所有模块正六边形的边长a=0.3 m，拼接曲面的曲率半径r=50 m，模块总数目为127，绕中心围成7 层。使用遗传算法求解获得了最优拼接曲面，该拼接曲面满足所有模块之间均不发生碰撞，且该拼接曲面的口径l值达到最小值6.77 m，此时为该条件下模块排列最为紧密的最优曲面，对应的参数取值分别为a0=0.000 027，a1=0.007 4，a2=0。重复运行50 次遗传算法，所得结果如图10 所示。

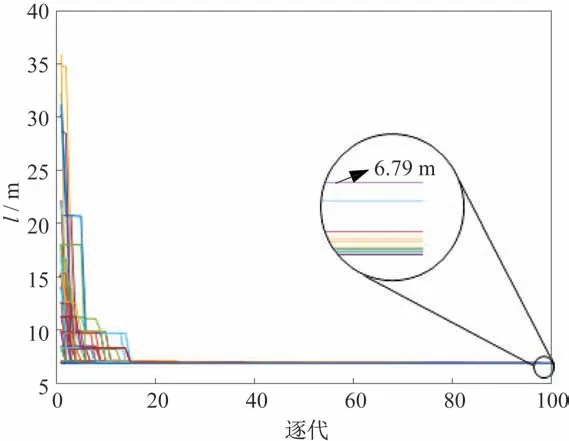
图10 运行50 次遗传算法后的口径结果Fig.10 Results of l after 50 iterations by the genetic algorithm

50 次结果的均值为6.77 m，且最后都可以稳定收敛到最优值处。从统计结果来看，优化算法所得到的曲面口径最小值结果稳定，可以有效得到最密拼接曲面。

4 结束语

本文提出了一种可以解决同构正六棱柱模块化航天器拼接后，组合体拼接曲面可以拟合为一个球冠时的所有模块位置求解问题的方法——平面辅助映射法，并在此基础上建立了拼接曲面的数学模型。本文采用改进的层次包围盒算法将六棱柱模块进行分割，从而解决了模块之间的CD 问题。最后采用遗传算法，解决了曲率半径变化范围和最优曲面求解的问题。

本文提出的平面辅助映射法中，模块化航天器的形状可以在未来衍生为立方体、四面体等任意形状，组合体拼接曲面中所有模块顶面近似的空间图形也可以衍生为抛物面、锥面等任意空间图形。