临近空间高机动目标二次滤波轨迹跟踪及预测

何君宇 宁国栋 王晓峰 张科南 王江华

北京机电工程研究所,北京 100074

0 引言

近年来,随着临近空间高速飞行技术的发展,各军事大国在临近空间高速飞行器领域的竞争也进一步加剧[1]。区别于传统飞行器,临近空间高速飞行器飞行在临近空间,具有机动性能强、飞行速度快、打击范围广的特点[2],现有防御系统难以对其进行有效拦截,其主要难点在于对来袭目标轨迹的准确跟踪及预测。现有文献大多是对于滑翔高速飞行器或高速飞行器短时机动跟踪及预测的研究[3-7]。

针对高速机动飞行器的轨迹跟踪预测问题,常采用以卡尔曼滤波(Kalman Filter,KF)为代表的滤波算法对目标相对距离、角度等原始信息进行加工,结合构建的目标机动模型,实现对目标轨迹的跟踪。因此滤波算法是目标轨迹跟踪及预测的关键技术。其过程主要分为2步:1)建立目标的机动模型;2)构建合适的滤波算法。

现有的高速目标的机动模型建立方法主要有2种:1)基于弹道方程,构建目标的动力学模型[8]。该方法先验要求过多,模型的鲁棒性差。2)基于目标的运动学统计特性,构建目标的机动模型,如CT模型、singer模型等。其优点是模型对于不同机动目标的适应性较强。而针对强机动目标的轨迹跟踪问题,常采用交互多模型滤波方式。其原理是依据目标的机动形式,建立多机动模型,分别进行滤波,并通过概率模型融合各通道的滤波结果,以获取目标的准确运动信息[9-11]。

滤波算法是在目标观测信息的基础上,结合模型信息,根据特定的滤波准则,得到系统状态的最优估计的算法。KF算法仅适用于线性高斯系统,而针对于复杂的非线性系统常常利用EKF、容积卡尔曼(Cubature Kalman Filter,CKF)等非线性滤波算法,由于在对非线性系统进行“线性”拟合的过程中,不可避免地丢失了某些系统信息,所以导致对非线性系统状态的估计量存在较大偏差,线性/非线性融合的滤波方式提供了一种解决思路。赵彦明等[12]针对捷联惯导系统大失准角下非线性滤波器状态维数过大的问题,提出了KF/EKF2混合滤波方法,验证了混合滤波算法性能优于单滤波算法。但是对于高速机动目标的跟踪问题,现有研究大多采用单次非线性滤波,对目标的运动状态跟踪精度不足。

由于实际跟踪过程中,环境、系统噪声、人为干扰等因素导致单一观测器的在进行长距离跟踪时效果不佳。多观测器协同跟踪是提升跟踪系统的稳定性及准确度的有效方式。文献[13]提出一种基于雷达和红外传感器优化数据压缩的跟踪信息融合算法,利用多传感器数据融合,实现信息互补,提高目标跟踪精度和识别能力。范成礼等[14]针对空天高速飞行器的多传感器协同跟踪的任务规划及优化算法进行研究,验证了多传感器协同观测能满足临近空间高速飞行器跟踪的要求。

基于跟踪目标获取的目标运动信息,可预测来袭目标的轨迹,提高拦截精度。翟岱亮等[15]等依据跟踪信息,采用最小二乘拟合实现对轨迹的预测,但其建模过程需要对飞行器的相关参数进行假设。文献[16]对滑翔式临近空间高速飞行器轨迹预测问题,提出了一种基于气动加速度经验模态分解(EMD)的轨迹预测方法,该方法需要对飞行器的气动特性进行一定的假设。文献[17]基于无人机动力学模型结合卷积神经网络预测出无人机轨迹。

本文针对临近空间高机动目标大范围机动飞行的轨迹跟踪及预测问题,提出了基于多观测器协同观测的二次滤波算法及基于ARIMA模型的轨迹预测方法。首先采用多观测器协同跟踪方法,对多观测器数据进行凸组合融合。其次针对临近空间高机动目标,建立多角速度的协调转弯模型,对单个观测器的原始数据采用交互多模型二次滤波方法,获取目标准确的速度及角速度信息。最后基于目标跟踪得到的运动状态信息,采用ARIMA模型对目标角速度进行预测,结合滤波模型中的预测步,实现了对运动轨迹的准确预测。

1 跟踪系统模型

1.1 状态模型构建

临近空间高速飞行器飞行阶段分为助推段、巡航段和俯冲段3个部分。图1为临近空间高机动目标机动飞行弹道。

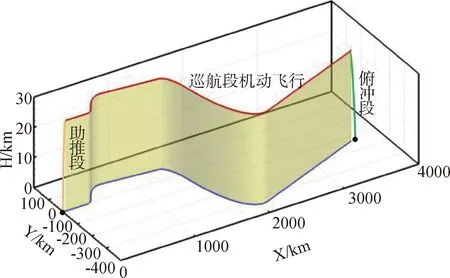
图1 临近空间高机动目标三维机动飞行示意图

临近空间高机动目标在巡航段的纵向机动性能较差,但其具有良好的横侧向机动能力[18]。因此本文重点分析临近空间高机动目标的横侧向机动运动的轨迹跟踪问题。

假设目标在飞向目的地的过程中为避开拦截区进行转弯机动。角速度为ω。

(1)

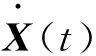
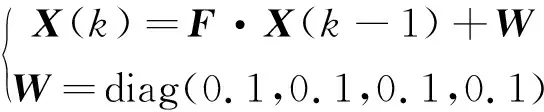
(2)

式中:F是离散状态转移矩阵,W是状态噪声,X(k)与X(k-1)分别表示第k步与第k-1步的系统状态,其包括x,y方向的坐标位置及速度。

(3)

角速度ω=0表示目标进行匀速直线运动,ω>0表示目标逆时针转弯,ω<0表示目标顺时针转弯。针对吸气式高速目标的机动性可通过匀速圆周运动的相关公式估算出目标的转弯速度的范围,即获取±ωmax。对运动模型的角速度取ωmax或-ωmax或0即可得到目标的三种运动模型。

1.2 观测模型

侦察卫星、雷达等观测器为跟踪系统提供目标运动的观测值,其对目标的量测信息一般为目标距离雷达的径向距离r(k)以及目标相对于雷达的方位角α(k),假设观测点位置为x0、y0。由此可得离散化系统观测模型如式(4)所示。

(4)

式中:V表示观测模型的系统噪声,取值为diag(1,0.1),Z(k)表示第k步系统的观测信息Z(k)=[r(k),α(k)]T,X(k)表示第k步系统的状态量,分别表示第k步目标位置(x(k),y(k))距离观测点(x0,y0)的x方向与y方向的相对距离。

2 轨迹跟踪算法

2.1 轨迹跟踪算法流程

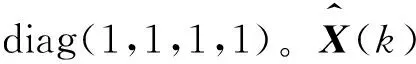
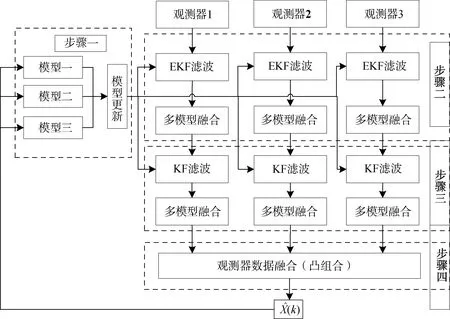
图2 临近空间高机动目标轨迹跟踪算法

步骤1:状态模型更新

依据目标的飞行状态进行多模型交互,获取更新后的3种状态模型。

步骤2:交互多模型非线性滤波

分别针对每个观测器的观测数据,采用EKF算法,结合3种状态模型做多模型融合滤波。

步骤3:交互多模型二次线性滤波

经过第2步滤波过程后,得到目标线性的轨迹信息,利用非线性滤波后的状态估计值作为线性滤波器的输入,利用多模型线性滤波的方式,对目标的速度及角速度信息进行跟踪匹配。

步骤4:多观测器数据融合

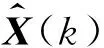
以下具体介绍所提出的临近空间高机动目标轨迹跟踪算法用到的模型与滤波算法。

2.2 非线性/线性融合二次滤波

针对观测系统为非线性的轨迹跟踪问题,采用EKF-KF二次滤波的方式进行滤波计算。首先利用单次非线性滤波算法对非线性系统进行滤波,再将滤波后得到的线性结果作为线性滤波的输入,通过二次线性滤波实现对目标运动状态的稳定跟踪。

1)单次非线性滤波

采用EKF对非线性的原始观测信息进行滤波,由前文对系统方程的推导,第k步系统方程表达式为:

(5)

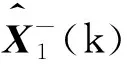
(6)

然后,利用雅可比矩阵通过线性KF算法即可获得卡尔曼增益Kk,再将先验状态估计值与观测值通过卡尔曼增益进行融合,获取最终的滤波结果。下标1表示第1次滤波结果。

2)二次线型滤波

通过EKF滤波过程后,得到目标的轨迹信息,利用非线性滤波后的状态估计值作为线性滤波器的输入,利用KF算法,对目标的速度及角速度信息进行跟踪匹配。线性滤波系统的系统方程为:

(7)

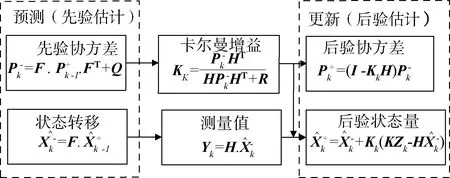
图3 KF算法

ω(k)=μ1(k)ω1(k)+μ2(k)ω2(k)+μ3(k)ω3(k)

(8)

式中:ω1(k),ω2(k)和ω3(k)分别表示第k步3种机动模型的角速度,μ1(k)、μ2(k)和μ3(k)分别表示第k步3种模型对应的概率,ω(k)表示第k步滤波得到的目标角速度信息。

2.3 交互多模型滤波

针对临近空间高机动目标的跟踪问题,目标存在匀速直线、转弯等多种机动形式,单一的直线运动或转弯模型无法有效表达目标运动特性,故采用交互多模型滤波的方式。

1)模型更新

在第k步,滤波开始前系统的状态模型分别对应着3个角速度ω1,ω2和ω2,按从大到小排列,其对应的模型概率分别为μ1(k-1),μ2(k-1)和μ3(k-1)。ω2设为中心模型,ω1设为右变模型,ω3设为左变模型,通过前文推导,模型的角速度取值范围为[-ωmax,ωmax],以[-ωmax,0,ωmax]为初始模型,每次滤波前通过模型概率的大小改变中心模型ω2,之后结合上一步的模型后验概率以及模型变化阈值,更新右变模型与左变模型。

2)多模型融合

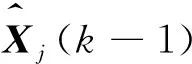
(9)

2.4 多观测器跟踪算法

针对临近空间高机动目标远距离机动飞行的轨迹跟踪问题,采用同源多观测器对目标进行跟踪。其原理是通过将多观测器的跟踪数据进行数据融合,从而解决单一观测器跟踪精度低、稳定性差的问题。数据融合的方式按模型结构可分为:分布式、集中式和混合式3种[20]。本文采用分布式的数据处理方式,即首先分别滤波处理每个观测器采集到的距离与偏角等位置信息,之后再将滤波后的目标轨迹信息进行数据融合。

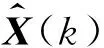
(10)

3 基于ARIMA模型的轨迹预测

3.1 ARIMA模型概述

ARIMA模型即是通过自回归模型(Autoregressive,AR)、移动平均模型(Moving Average,MA)以及差分过程构建的时间序列模型。其步骤一般包括:数据平稳性检验、模型参数确立、构建时间序列、模型预测、模型准确性评估。模型参数一般包括p,q和d分别对应自回归项、移动平均项以及数据平稳化的差分次数。

由于时间序列常常为非平稳序列,所以需要利用差分环节对时间序列进行平稳化处理。通过单位根(Augmented Dickey-Fuller,ADF)检验及非线性趋势(Kwiatkowski-Phillips-Schmidt-Shin,KPSS)检验,判断时间序列的平稳性,确定模型的参数d。AR描述当前值与历史值之间的联系,用变量自身的历史时间数据对自身进行预测,p阶自回归过程的公式为:

(11)

式中:yt是当前值,μ是常数项,p是阶数,表示当前值与多久前的值有关,γi是自相关系数,εt是误差。移动平均模型(MA)关注的是自回归模型中的误差项的累积。q阶自回归过程的公式为:

(12)

移动平均法能有效消除预测中的随机波动。在获取平稳序列后,即可通过ACF与PACF函数根据表1,选取p和q的值,从而构建ARIMA预测模型。

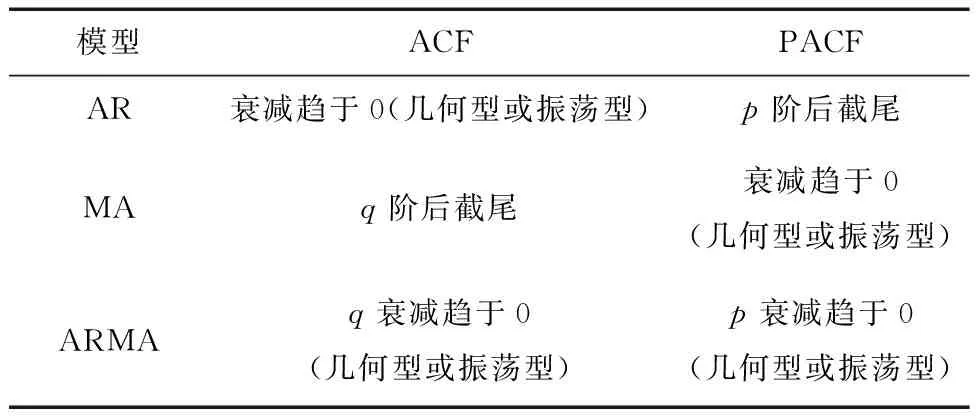
表1 p、q参数确定规则

3.2 基于ARIMA模型轨迹预测

通过对目标运动状态的准确跟踪滤波,可以获得目标准确的角速度时间序列信息,基于此对目标的轨迹进行预测。算法的流程如图4所示。

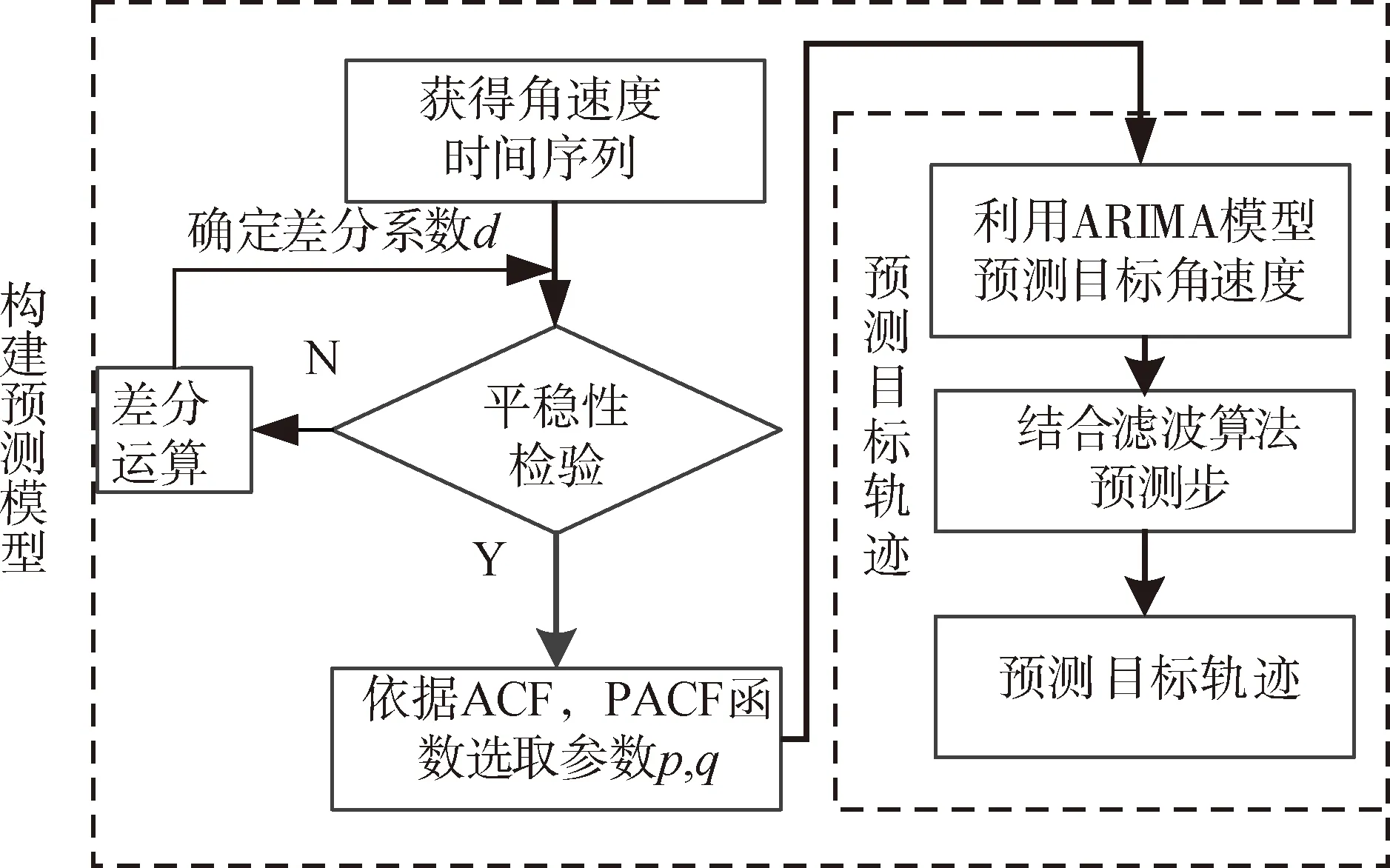
图4 轨迹预测算法

1)平稳性分析:判断角速度序列信息的平稳性,依据ADF和KPSS检验确定系统的差分系数d。

2)模型参数选取:依据平稳的序列信息,绘制其ACF与PACF函数的图像,根据p,q函数的确定准则,选取适合的p,q值,从而构建系统的ARIMA预测模型。

3)角速度预测:依据ARIMA模型,预测目标的角速度信息。

4)轨迹预测:将预测出的角速度序列代入滤波算法中的预测步,实现对飞行器轨迹的预测。

4 仿真校验

4.1 目标运动轨迹

考虑在平面直角坐标系内描述飞行器的运动轨迹。假设目标的初始位置x0=0km,y0=0km,初始速度为vx0=2km/s,vy0=0km/s。飞行航迹中避让2个障碍区,其中心坐标分别为(650km,-406.2km)与(2011.2km,202.69km),障碍区半径为500km。本文考虑目标飞行过程中发现需避让的障碍区后,采用最大过载进行机动飞行;随后,通过临近空间高机动目标巡航段的飞行速度,可估算出目标的最大角速度。当目标飞离障碍区后,即以最小能量损失飞行方式,沿障碍区切线方向直线飞向目的地。

目标飞行过程分为7个阶段:t=1～150s,目标沿初始方向匀速飞行;t=151～203s,目标以角速度ω=0.01rad/s调整飞行角度;t=204～342s,以角速度ω=-0.004rad/s进行匀速转弯飞行,绕过障碍区;t=343～712s,目标沿障碍区切线方向匀速直线向目的地飞行;t=713～816s,目标抵达第2障碍区附近,以角速度ω=0.01rad/s进行匀速转弯飞行,调整飞行航向角;t=817～1133s,以角速度ω=0.004rad/s进行匀速转弯飞行,绕过障碍区;t=1134～1893s,目标沿障碍区切线方向,以最短距离向目的地飞行。

单观测器的位置为(550,-150)km,多观测器位置分别为(550,-150)km、(2230,100)km、(3200,100)km。采样周期为0.2s,观测噪声取值为diag(1,0.1),状态噪声取值为diag(0.1,0.1,0.1,0.1)。

4.2 多观测器跟踪仿真

针对临近空间高机动飞行器,本文利用交互多模型EKF滤波算法分别对单观测器跟踪和多观测器跟踪进行了仿真校验。并令X方向位移误差为δx(单位km),3种模型的概率转移矩阵如式(13)所示。

(13)

由图5和6可发现随着目标运动距离的增加以及目标出现机动飞行,观测器的跟踪效果不断下降,而多观测器跟踪效果良好,X方向与Y方向轨迹跟踪误差在0.5km范围内。原因是单一观测器关于目标的观测信息随着距离的增加以及目标航迹角的变化,观测误差不断增加,最终出现发散现象。而多观测器在多个不同位置对目标进行观测,通过凸组合的数据融合算法对多个观测器的观测数据进行融合,相对于单观测器,其对于飞行轨迹的跟踪效果显著提升。

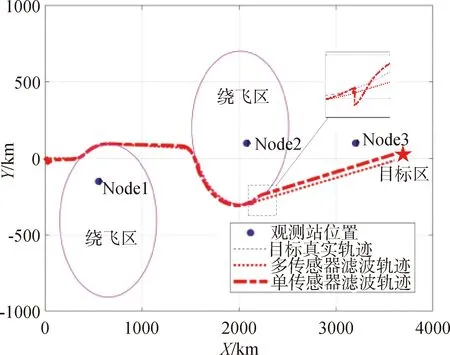
图5 单观测器与多观测器轨迹跟踪

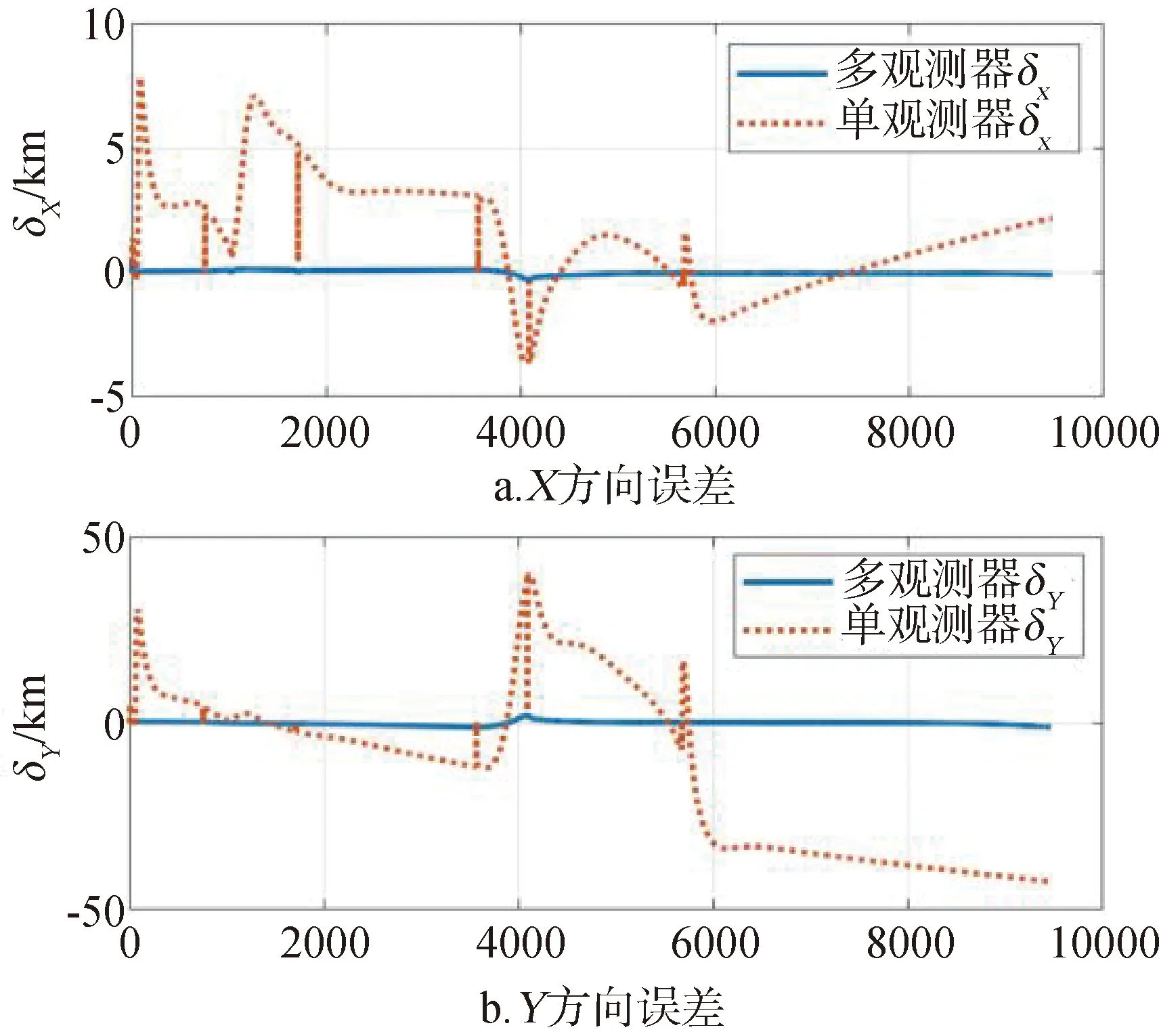
图6 X,Y方向位移误差对比

4.3 交互多模型二次滤波仿真结果分析

采用单次PF与EKF算法与二次滤波算法进行对比。PF算法是通过非参数化的蒙特卡洛模拟方法实现滤波,其核心思想是利用一系列随机采样粒子的加权和来表示后验概率密度。PF采样粒子数为200个。X方向速度跟踪误差为δvx,角速度跟踪误差为δω。由图7可发现,2种单次滤波方法得到的角速度跟踪值存在较大的误差,而二次滤波后的角速度跟踪十分稳定,误差在5%以内。对于速度跟踪,如图8所示,单次滤波算法,对速度、角速度的跟踪出现较大误差,二次滤波在X与Y方向速度跟踪误差都在2%以内,可准确地跟踪目标的飞行速度,跟踪效果优于PF与EKF单次滤波算法。二次滤波算法通过线性/非线性滤波融合滤波的方法,实现了对系统状态量的准确跟踪。

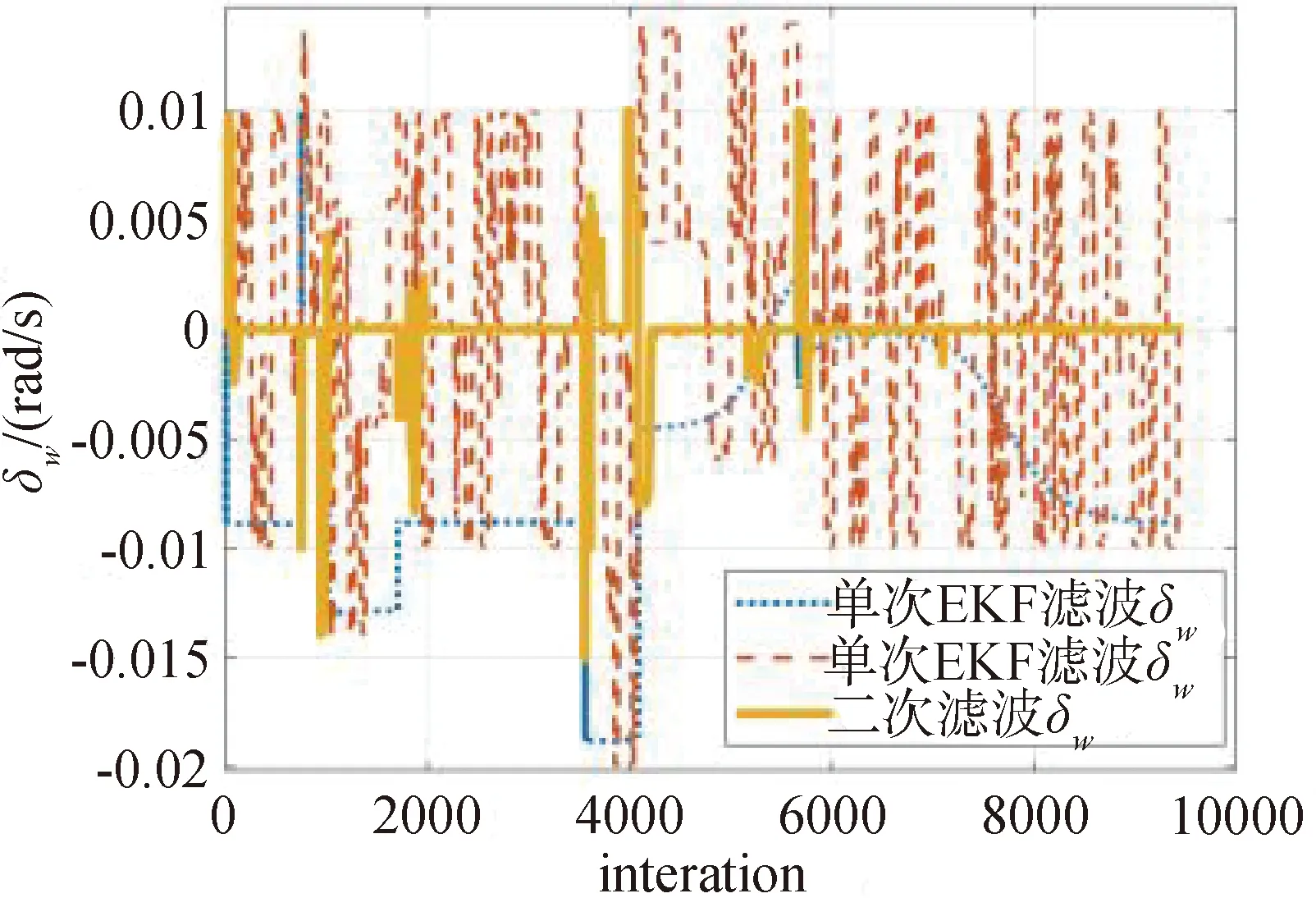
图7 角速度跟踪误差

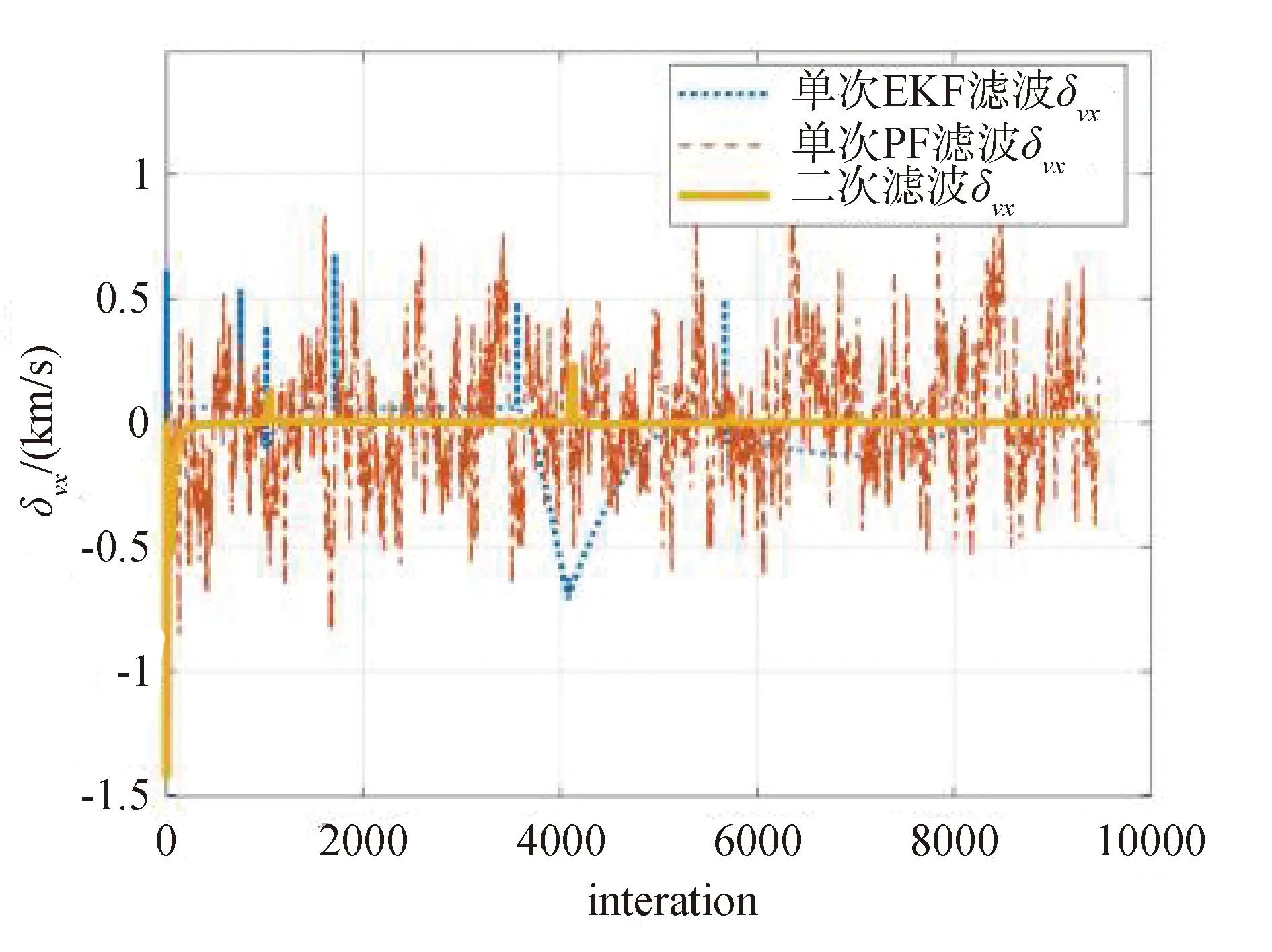
图8 X方向速度跟踪误差

依据轨迹跟踪获取的角速度信息,利用ARIMA模型拟合角速度的时间序列模型,对接下来1000步的角速度进行预测,之后结合目标机动模型预测目标运动轨迹。采用300步跟踪角速度信息,由于ARIMA模型要求拟合序列满足平稳性需求,所以先对角速度序列信息进行平稳化处理,由3.1节表1对p,q值选择的准则,结合图9可知,ARIMA预测模型的p=6、q=7时,能够满足ACF与PACF函数值都在95%置信区间内。即说明,当AR模型参数p取6以及MA模型参数q取7时,AR模型与MA模型共同构成的ARIMA时间预测序列对真实目标时间序列的拟合程度最好,误差最小。预测序列模型如式(14)所示:式中y(t)表示预测的值,e(t)表示预测值附近的误差值,通过该ARIMA时间序列预测模型,可较好地预测目标轨迹。

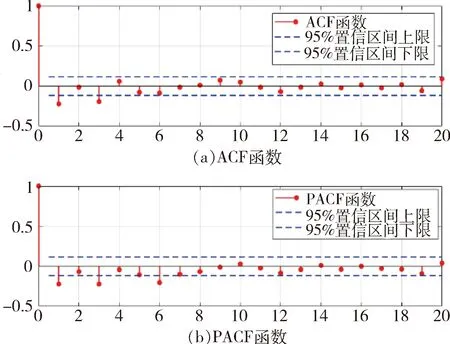
图9 PAC与PACF函数

(14)

由图10可知,依据目标过去300步的角速度信息,通过ARIMA模型可预测出目标将来1000步的角速度信息。

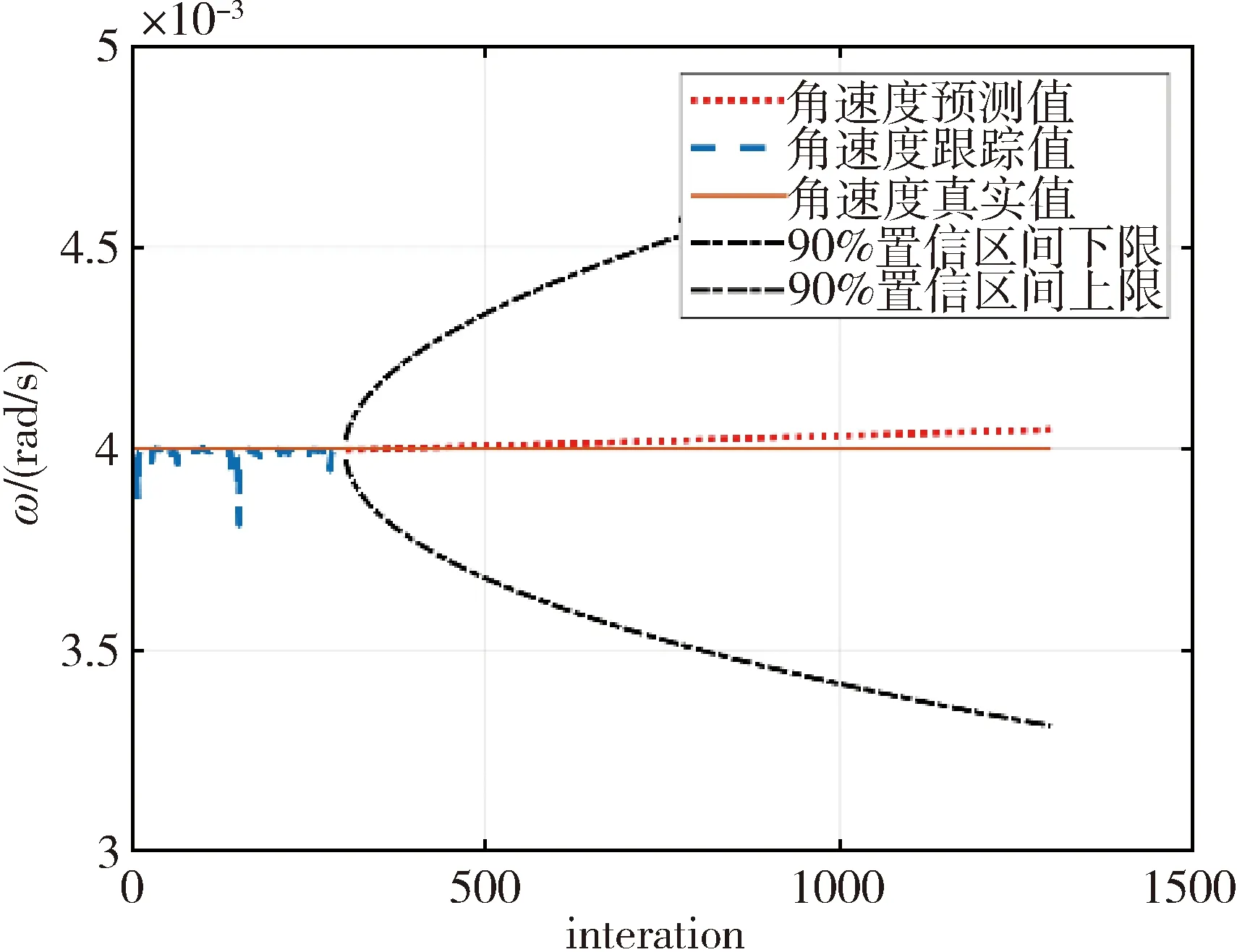
图10 角速度预测结果

结合预测的角速度信息与滤波算法的预测步预测目标轨迹。如图11所示,发现预测误差在1000步以内都保持在较小范围,预测误差不超过0.5km。说明该方法可有效预测目标的运动轨迹。由于该方法无需以大量的先验信息作为基础,提高了轨迹预测算法的工程实用价值。

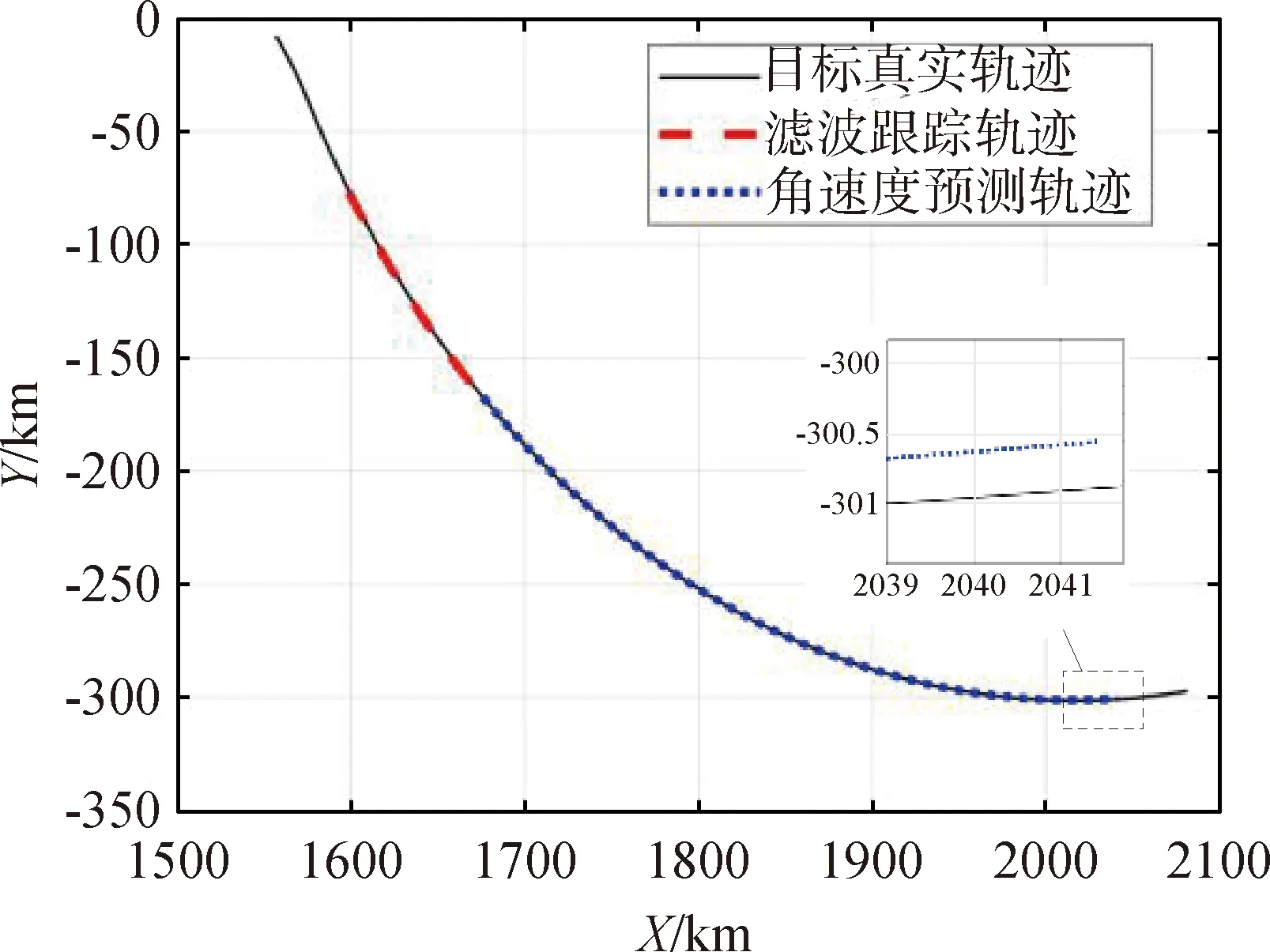
图11 轨迹跟踪及预测结果

5 结论

发展了基于多传感器协同观测的交互多模型二次滤波算法,角速度跟踪误差从30%降低到5%以内,速度跟踪误差从20%降低到2%以内。构建了基于ARIMA模型的轨迹预测算法,可实现对机动目标未来100s时间内运动轨迹的稳定预测,误差不超过0.5km。对临近空间高机动来袭目标的拦截问题提供了一种有效的解决策略。