基于权重扰动机制模拟退火遗传算法的景德镇陶瓷文化景区旅游路径规划

汤可宗，刘 康，刘宇娇

（景德镇陶瓷大学 信息工程学院，江西 景德镇 333000）

0 引言

21 世纪以来，我国在加快经济发展进程的同时，也逐渐将文化传承旅游项目囊括其中，进一步推动国家文化知识产业发展，促使文化传承和延续［1］。江西省景德镇市作为世界著名的“瓷都”，制瓷历史悠久，被誉为“中国地标”，是中国国家首批历史文化名城。然而，由于景德镇地处多山环绕的丘陵地带，导致景德镇市旅游业经济发展较为缓慢，也使得景德镇陶瓷文化的传播和影响范围较小。因此，为了提高景德镇陶瓷文化知名度，需对景德镇陶瓷文化景区进行旅游路径规划。

路径规划是指在规定的区域范围内使目标对象以较短的时间或较小的距离为代价规划出一条合适的路径［2-3］。其中，常见的路径规划技术［4］分为传统算法［5-6］、基于几何模型算法［7-8］、仿生智能算法［9-10］和深度学习［11-12］。由于不同的旅游景区在地域分布上有所不同，常常会影响游客观光游览的体验和兴趣度，导致旅游区域的经济收益和文化传播程度较低，因此，需要提出一种合理的旅游路径规划算法，既可以有效地引导人群进行游览，也可以为当地经济和文化传播产生积极影响。许多研究者对此展开研究，并取得系列研究成果。例如，谭波［13］提出一种基于蚁群算法的旅游区最优人群导游路径规划模型，将影响旅游区人群导游规划的主要因素作为最优路径规划的曲折程度约束，设定时间和路径总长约束，对目标函数进行求解，最终规划出的路径结果更为优化。黄腾［14］提出一种基于遗传模拟蚁群算法的旅游路径规划，首先建立满足约束条件的环境数学模型，然后使用遗传算法对需要规划的景区进行路径优化，最后使用蚁群算法进行二次优化，降低了运算复杂度，缩短了路径规划时间，也为旅游爱好者提供了便捷服务。Damos 等［15］提出一种基于多目标遗传算法的新型城市旅游路径规划方法，采用新的参数提高遗传算法精度，并结合外部和内部旅游地潜力选择最优旅游路径，同时采用层次分析（AHP）方法对多个冲突目标下的城市旅游线路规划进行评价，使得规划出的路径更加准确和直观。Xu 等［16］在NSGA-Ⅱ（支配排序遗传算法）的基础上引入自适应概率和2-opt 局部搜索策略，提高了算法的收敛性和多样性。邹时林等［17］以庐山为实例，对最短路径算法进行改进，将景点的知名度和停留时间作为各景点之间边的权值，最终得到的路径可以满足大部分人群的需求。Liang 等［18］提出一种改进的蚁群优化算法，在信息素更新策略中结合景区天气、舒适度等情景信息，使信息素更新趋于适合游客的路径。同时，在算法中引入路径支持度对路径进行评价，避免算法陷入局部最优。Lyu［19］为提高算法执行效率和实时性，构建了基于边缘云协同计算的实时计算框架进行路径规划。在每个控制决策周期，移动机器人从边缘获取感知数据并传输到云端，并且通过流计算云实时规划路径，利用云的存储容量，实现环境记忆，提高了路径规划效率。

上述规划模型，虽然可以有效缩短路径规划时间，满足最优路径需求，但是在算法收敛速度等问题上仍需进行优化，为此，本文结合当地实际情况提出一种基于权重扰动机制的模拟退火遗传算法（Weighted Disturbance Mechanism Annealing Genetic Algorithm，WDMAGA）。首先，随机生成初始种群；然后，根据景区分布区域及周边交通情况设计带权重扰动机制的路径评价准则，在路径长度基础上，通过分析不同景点之间的距离长度，设定不同的权重值对路径评价函数进行扰动变化，同时在评价准则中融入温度退火因子，进一步精确路径评价准则；最后，根据构建的模拟退火交叉和变异算子，使交叉与变异随搜索过程自适应变化，从而更好地区分出种群中的优劣个体，增强种群个体多样性。WDMAGA 能够较好地针对景德镇陶瓷文化景区进行旅游线路的路径规划，且规划出的路径真实有效，可为游客优化旅游路线提供指导。

1 环境分析

景德镇市位于江西的东北部，地形多为丘陵和山地，是典型的江南红壤丘陵区，主要分为景德镇市市辖区（珠山区、昌江区、浮梁县）和乐平市，其在市区内平均海拔为32 m，而在省界接壤地带海拔最高至1 618 m。由于景德镇市的地势呈现出由东北向西南倾斜趋势，导致其文化景区在地域上分布不均匀。根据景德镇陶瓷文化景区的经纬度坐标，生成景德镇市景区分布缩略图，如图1所示。

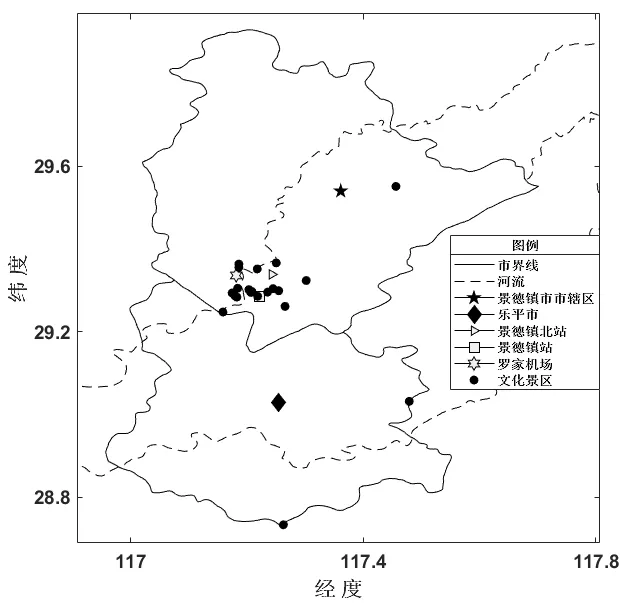
Fig.1 Thumbnail of Jingdezhen ceramic culture scenic spots distribution图1 景德镇陶瓷文化景区分布缩略图

可以观察出，景德镇市的陶瓷文化景点多以点状散列分布于景德镇市中部区域，这是因为相对于景德镇市偏远的山区县镇，其中部区域经济相对发达、交通相对便利，符合人群对便捷旅行的需求。

此外，本文根据已知资料对景德镇陶瓷文化资源进行统计，划分出具有旅游价值的优质旅游资源，如表1 所示。可以明显发现，景德镇陶瓷文化景区多分布于珠山区，部分分布于昌江区和浮梁县，只有极少数景区分布于乐平市。因此，本文综合景德镇市文化景区分布、交通便捷程度、经济发展潜能等相关因素作为旅游路径规划过程中的选择指标。

2 权重扰动机制模拟退火遗传算法

2.1 权重扰动机制路径评价准则

路径评价准则是对每条路径优劣程度的评判标准，也是对后期是否保留该路径的判断依据。在对景区旅游路线路径规划过程中，不同景区所在地理位置周边分布有所区别，为了较为客观地反映规划路径的合理性，在设计路径评价函数时，需要考虑景区所处位置以及两两景区之间的交通环境。本文将路径长度作为评价路径优劣程度的主要因子，并在评价准则中引入交通环境因子对路径长度进行权重扰动，同时融入模拟退火算法中的温度退火因子T［20］，通过控制退火因子T使适应度函数FIT自适应变化，进而在选择操作过程中增加种群多样性，使得到的路径评价值更加接近实际情况，计算公式为：

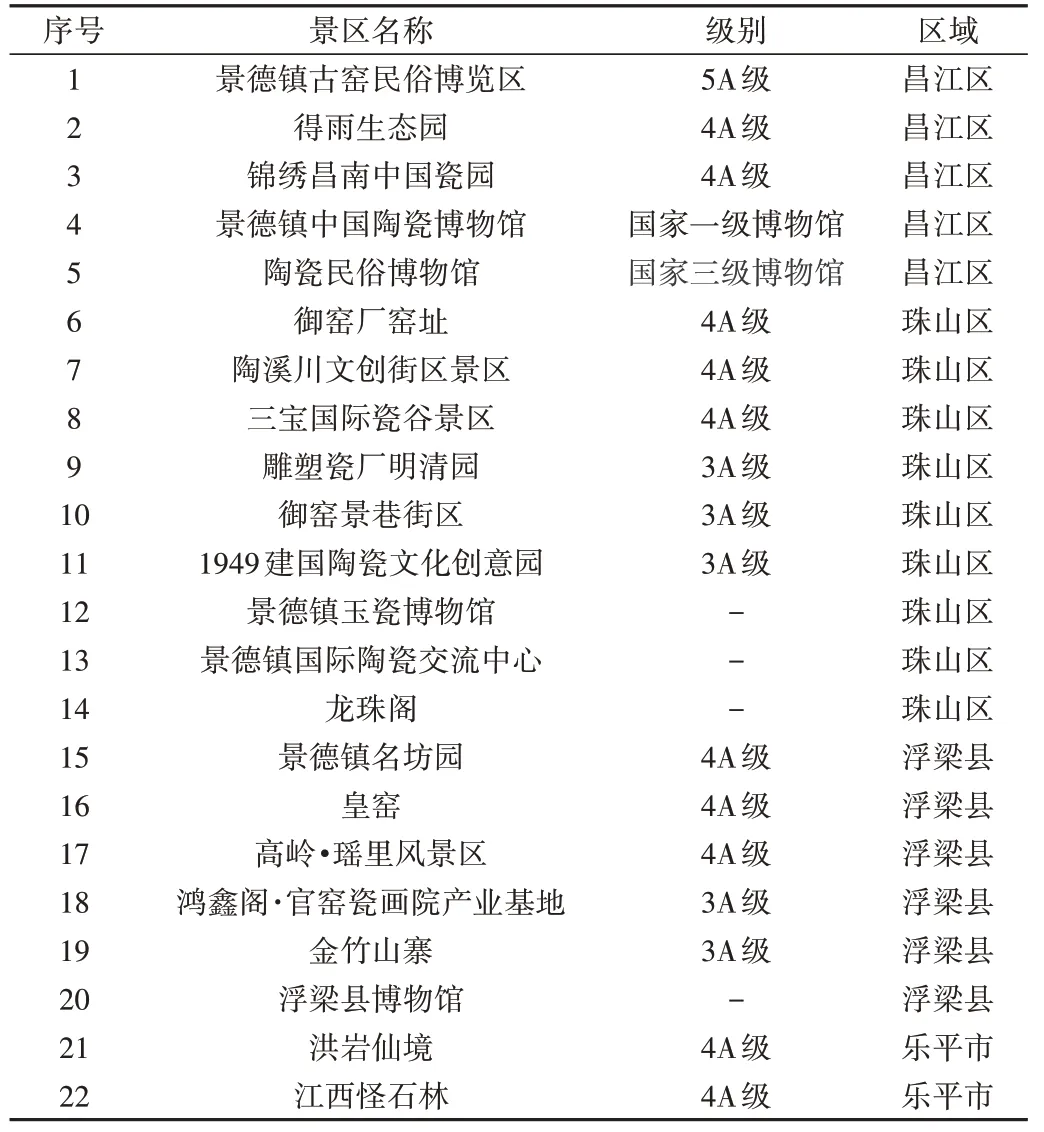
Table 1 Statistical data of Jingdezhen ceramic cultural scenic spot表1 景德镇陶瓷文化景区统计资料

式（1）中，ω表示不同景点之间交通情况权重因子，主要根据Google 地图中景德镇不同景区之间的交通分布和区域分布对景区之间距离的影响进行取值范围的规划，ω的取值如表2 所示。ε表示温度终止条件，一般取值为0.000 1。Dij表示景点i和景点j之间的距离，其中，j=2，3，4…n。由于本文通过GPS 获取的景点坐标值为经纬度坐标，因此，为计算真实地图上不同景点之间的距离，采用Haversine 公式［21］根据两个景点的经纬度坐标计算相关距离值，其中，Haversine 公式为：

式（2）中，φ1和φ2分别表示两个景点纬度；Δλ表示两个景点经度差值，R表示地球半径，一般取值为6 371Km。

Table 2 Changes of ω values表2 ω取值变化情况

2.2 遗传操作

2.2.1 模拟退火交叉算子

遗传算法中的交叉概率一般设为固定值，某种程度上不利于种群个体多样性的有序分布。在此，引入退火因子T使用余弦函数构造自适应交叉概率函数，可有效增强种群个体间的自由交叉度，有利于种群间个体多样性的自由分布。自适应交叉概率函数如下：

式（4）和式（5）中，K是介于（0，1）的常量因子；γ为启发示交叉因子；PCU与PCL是给定的自适应交叉概率的上下限值；minf是可行路径最小适应度值；meanf是可行路径平均适应度值；maxf是可行路径最大适应度值。当最小适应度值不等于平均适应度值，且退火因子T大于临界值0.000 1 时，将采用式（4）中第一个算式对交叉概率PC进行计算，以确定此时PC的值，反之，则使PC为常量0.8。个体交叉时将根据产生的介于（0，1）的随机数，与交叉概率PC进行比较确定是否进行交叉。

2.2.2 模拟退火变异算子

类似于上述自适应交叉算子，本文在变异算子中引入模退火因子T，构建一种新的自适应变异方式使变异概率随进化过程作自适应变化，其公式表示为：

式（6）和式（7）中，W是介于（0，1）的常量因子；φ为启发示变异因子；PMU与PML是给定的自适应变异概率的上下限值；f为个体的适应度值。当变异个体的适应度值大于等于平均适应度值，且退火因子T大于临界值0.000 1 时，将采用式（6）中第一个算式对变异概率PM进行计算，以确定此时PM的值，反之，则使PM为常量0.1。在个体进行变异过程时，将变异概率PM与产生的介于（0，1）之间的随机数进行比较。若后者小于前者，则从路径中随机选择两个不包含起点与终点的栅格路径点，对这两个路径点中的路径进行重新初始化，反之，则不需对该个体进行变异操作。

2.3 WDMAGA算法流程

WDMAGA 算法流程如图2所示，具体执行步骤如下：

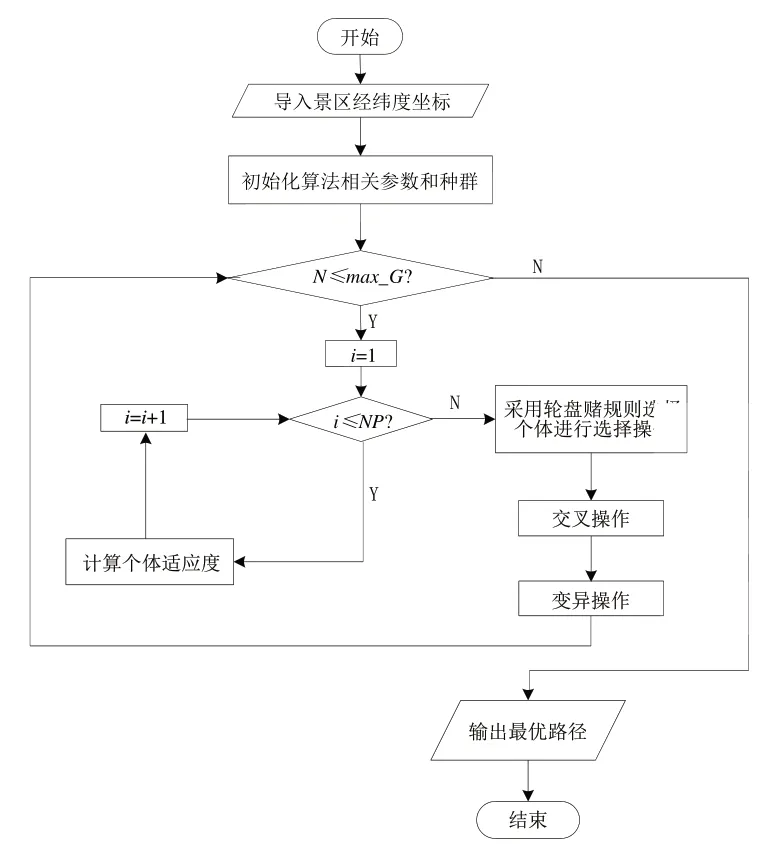
Fig.2 WDMAGA algorithm operation flow图2 WDMAGA算法操作流程

Step1：参数初始化。导入景德镇景点分布经纬度坐标和地球半径R，设置种群数目NP，个体染色体长度M，最大进化次数max_G，交叉概率PC、PCU、PCL，变异概率PM、PMU、PML，初始温度T，温度终止条件ε，交通环境因子ω等。

Step2：种群初始化。针对景点进行随机初始化设置。

Step3：适应度评价。根据适应度评价公式（1）计算个体适应度值，作为个体评价指数。

Step4：遗传操作。采用轮盘赌规则对当前种群进行选择操作，并根据评价指数及模拟退火因子T，按照式（4）—式（7）分别对当前种群进行交叉、变异等遗传操作。

Step5：终止操作。若算法终止条件满足，输出种群中最优个体表示的最优路径，否则算法转Step3。

2.4 算法复杂度分析

在WDMAGA 中，其复杂度主要包括种群初始化过程与种群优化过程两个方面。在种群初始化过程中，采用随机生成初始种群的方式，故在执行种群初始化的过程中，所需复杂度为O（NP）。种群优化过程分为选择、交叉、变异3 个部分，选择操作的计算复杂度为O（NP），交叉操作的计算复杂度为O（M*NP），变异操作的计算复杂度为O（M*NP）。因此，执行一次种群优化过程所需计算复杂度为O（M*NP）。故ASAGA 算法在执行进化次数达到最大进化次数max_G的情况下，所需计算复杂度为O（max_G*NP（NP+M））。

3 仿真实验

为了验证算法的有效性，针对表1 中覆盖的景德镇陶瓷文化旅游景区资源，进行两组仿真实验。第一组主要分析算法中交叉算子PC、变异算子PM以及权重ω等参数的取值情况对旅游路线规划的影响效果。第二组主要将提出的算法与精华蚁群算法（EAS）［22］进行仿真结果对比，进一步说明提出算法的可行性。实验环境为：操作系统Windows 10，处理器Intel core i5-6200U，内存12GB。

3.1 算法参数组合分析

参数的不同取值对算法运行情况会产生一定影响，因此，为保证算法在实际应用中能够产生较好的规划效果，针对WDMAGA 算法中部分参数进行取值变化分析。该分析过程主要分为3 个部分：①分析式（3）中涉及的交叉算子PC的参数取值对算法规划效果的影响；②分析式（4）中涉及的比变异算子PM的参数取值对算法规划效果的影响；③针对路径评价准则中ω扰动权重取值范围对算法运行影响进行分析。种群规模NP仍设置为30，最大迭代次数max_G仍为100，交叉概率上下限PCU和PCL分别设置为0.9和0.2，变异概率上下限PMU和PML保持为0.1和0.01。

3.1.1 Part 1

为验证交叉算子PC的参数取值对算法的影响，结合遗传算法［23］中交叉算子的取值范围［0.6，0.9］，将交叉算子PC作如表3 所示的取值分析。其中，为了客观反映参数取值对算法规划最优路径的影响，表中数据的值均为算法运行10 次后的平均值，Max、Mean、Std、Best Path Value 分别表示算法运行10 次后最优路径长度的最大值、均值、标准差和最小值。算法在不同交叉算子取值情况下运行10 次得到的最优路径长度变化曲线比较如图3所示。

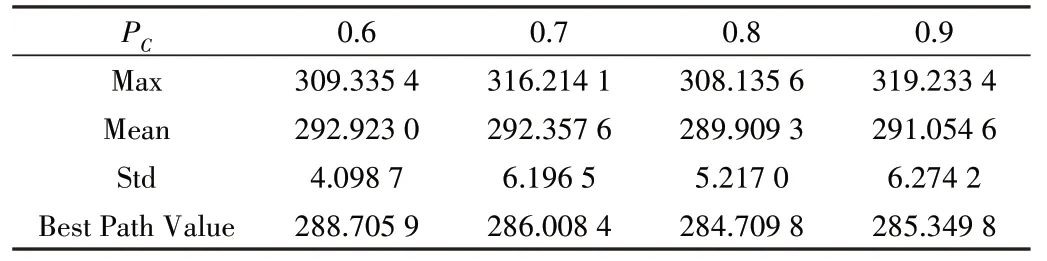
Table 3 Changes in PC parameters表3 PC参数取值变化

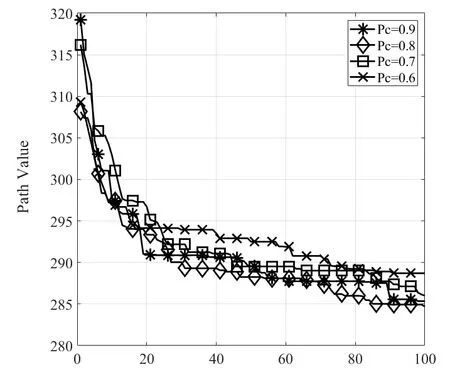
Fig.3 Comparison of optimal path lengths under different crossover operator values图3 不同交叉算子取值下最优路径长度变化比较

从图3 中4 组最优路径变化曲线可以发现，不同交叉算子的取值会影响算法最优路径长度的收敛状况。当PC为0.9 和0.7 时，算法在搜索前期极易产生偏离最优路径的最大值，使得算法在收敛至最优解时会经历较长时间和较多次数，进一步导致算法搜索速度缓慢。相对地，当PC为0.8 和0.6 时，由于进化前期搜索到的最优路径长度较为较为接近于最优解，使得算法在后续搜索过程中易收敛至最优状态。特别地，当PC为0.8 时，最优路径长度变化曲线收敛至最优解的迭代次数以及最优解的值都为4 组参数中的最小值。此外，从表3 中关于算法运行10 次后的最优路径长度的最大值（Max）、均值（Mean）也均为4 组参数中的最小值。这也说明相较于其他取值，当PC为0.8 时，会对算法运行效果产生较优影响。

3.1.2 Part 2

为验证变异算子PM的参数取值对算法的影响，结合遗传算法［23］中变异算子的取值范围［0.01，0.1］，将变异算子PM作如表4 所示的取值分析。其中，为了客观反映参数取值对算法规划最优路径的影响，表中数据的值均为算法运行10 次后的平均值，Max、Mean、Std、Best Path Value 分别表示算法运行10 次后最优路径长度的最大值、最小值、标准差和均值。算法在不同变异算子取值情况下运行10次得到的最优路径长度变化曲线比较如图4所示。

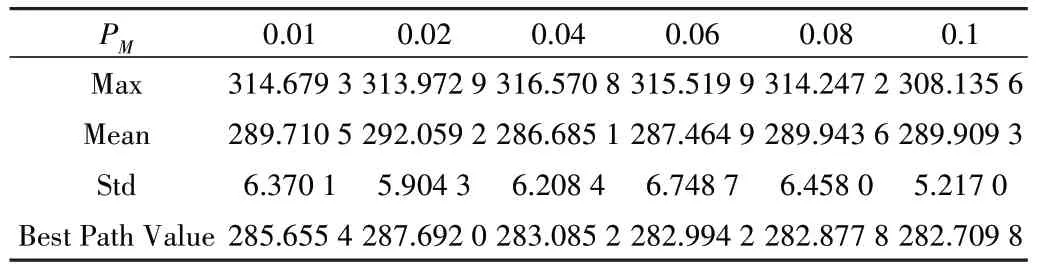
Table 4 Changes in PM parameters表4 PM参数取值变化

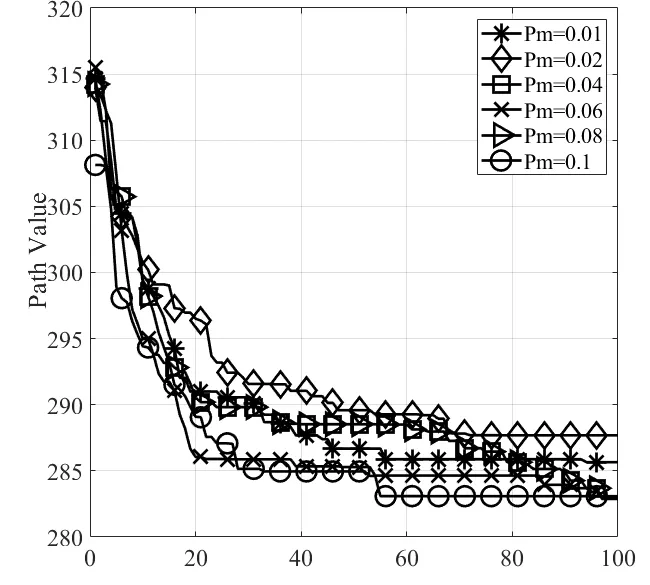
Fig.4 Comparison of optimal path length changes under different mutation operator values图4 不同变异算子取值下最优路径长度变化比较

从图4 中可以发现，当变异算子为0.04 时，算法得到的最优路径长度变化更加剧烈，且在搜索前期易产生偏离最优路径解的最大值，导致算法在向最优解的收敛过程中出现多次波动情况。当变异算子为0.01、0.06、0.08 时，算法在搜索前期能够搜索到的最优路径长度普遍处于340左右，尽管这个值相较于最优解仍有一定距离，但是可以较快地收敛至最优状态。当变异算子为0.02 和0.1 时，在搜索前期最优路径长度值保持在6 组参数取值中最接近最优解的环境下，且随着进化过程的推移，可以极快地收敛至最优解。至此，可以分析出当变异算子在0.02 或0.1时，算法可以得到较好的结果。然而，结合表4 中算法运行10 次后最优路径长度的最大值（Max）、均值（Mean）、标准差（Std）可以发现，相对于变异算子为0.02 时，变异算子的值为0.1 时得到的最大值、最小值、标准差以及10 次平均最优路径值更小，这反映出当PM为0.1 时，会对算法运行效果产生较优影响。

3.1.3 Part 3

在WDMGA 算法中，为了更加接近实际情况，在路径评价准则中加入ω扰动权重。本组实验为验证不同权重扰动值对算法在路径规划过程中产生的影响，将ω扰动权重分为如表5 所示的5 组组合。其中，为了客观反映参数取值对算法规划最优路径的影响，表中数据的值均为算法运行10 次后的平均值，Max、Min、Std 分别表示算法运行10次后最优路径长度的最大值、最小值和标准差，D表示景区之间的距离（单位为：Km），算法在不同权重取值情况下运行10次得到的最优路径长度变化曲线比较如图5所示。

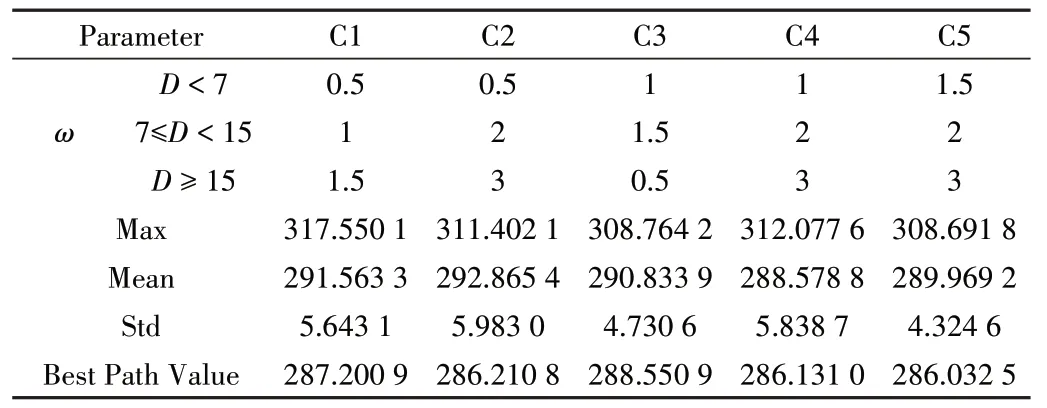
Table 5 Changes in ω parameters表5 ω参数取值变化

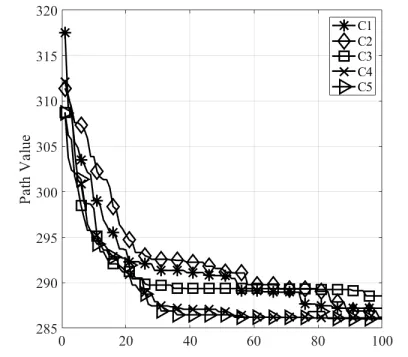
Fig.5 Comparison of optimal path lengths under different ω values图5 不同ω取值下最优路径长度变化比较

观察图5 中5 种参数组合进行10 次运行后得到的平均最优路径长度变化曲线可以发现，针对ω扰动权重的取值为C5 组合时，算法的最优路径长度变化整体趋于更优，且在搜索前期算法搜索到的最优路径值也更加趋近于最优解，这使得算法在后期收敛至最优解的时间更快。同时，分析表5 中关于不同组合得到的最优路径长度的最大值（Max）、均值（Mean）、标准差（Std）也可以得出，当扰动权重ω取C5中数值时，算法运行效果更好。

3.2 算法有效性分析

本组实验将WDMGA 算法与精华蚁群算法（EAS）［22］进行数据比较分析，进一步验证提出算法的有效性和可行性。算法相关参数设置为：种群规模NP=30，最大进化代数max_G=100，交通情况权重因子ω的取值变化如表2 所示，初始温度T=100，退火速度ρ=0.8，终止温度参数ε=0.001，交叉概率上下限PCU=0.9、PCL=0.2，变异概率上下限PMU=0.1、PML=0.01。仿真结果如图6、图7 所示，其中，图6 表示两种算法对景德镇陶瓷文化景区旅游资源规划出的最优路线，具体路线经过的景区如表6 所示。图7 表示两种算法在仿真实验中得到最优规划路线的平均路径长度和最优路径长度变化曲线比较，两种算法的数据统计结果如表7 所示。其中，Max、Mean、Min、Std 分别表示平均（最优）路径长度的最大值、均值、最小值和方差等统计数据。

在景德镇市地图中分别绘制出使用EAS 和本文提出的WDMGA 算法规划出的旅游路线图如图6 所示。可以分析出，两种算法均是依据陶瓷文化景区的地理分布进行的合理规划，相较于EAS 算法，WDMGA 算法规划出的旅游路线更符合游客观光的心理，并且也更有利于景德镇陶瓷文化的传播，这从表6 也可以看出。同时，分析表6 中WDMGA 算法对景德镇陶瓷文化景区的具体路线规划可以得出，在整个旅游过程中，首先让游客领略到景德镇的风景文化，然后在游玩过程中穿插着对景德镇陶瓷文化的讲解，最后让游客体验到来自不同方面的文化气息。在游客感受景德镇风土人情的同时，可以使游客更加了解景德镇陶瓷文化，并且产生浓厚的兴趣。

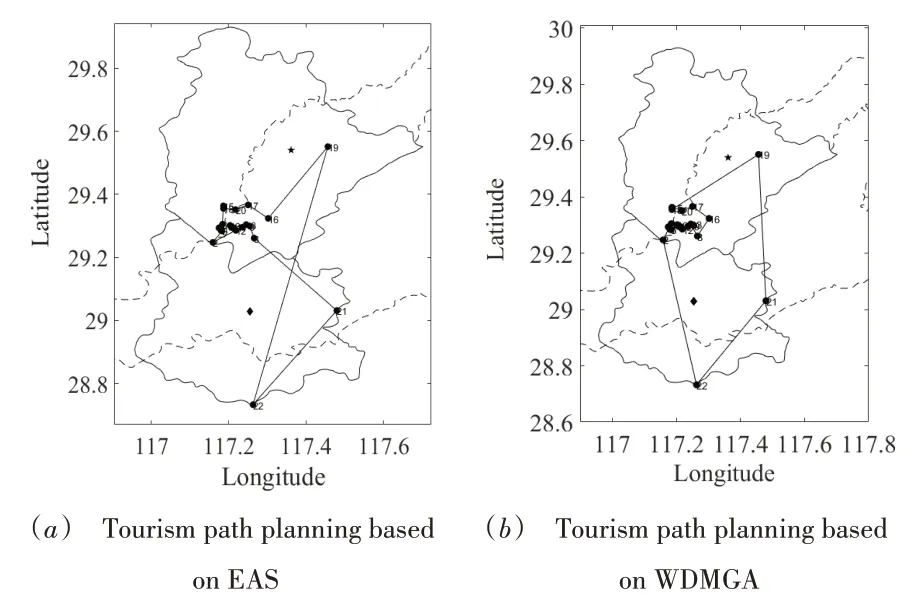
Fig.6 Tourism path planning with different algorithms图6 不同算法的旅游路径规划

Table 6 Tourism route planning of Jingdezhen ceramic culture scenic spot表6 景德镇陶瓷文化景区旅游路线规划

图7 反映出两种算法在对景德镇陶瓷文化景区路径规划时平均和最优路径长度随进化过程变化的曲线图。通过分析图7（a）关于EAS 和WDMGA 算法规划的平均路径长度变化曲线可以得出，在同等条件下，相较于受信息素影响的EAS 算法，使用WDMGA 算法规划出的路径的平均路径长度曲线变化波动幅度较小，且随进化过程得到的平均路径值均小于EAS 算法得出的平均路径值。同时从图7（b）关于两种算法的最优路径长度变化曲线也可以观察出，WDMGA 算法在15 次左右的进化过程时最优路径长度变化曲线已经收敛到最优且保持平稳变化，然而，EAS算法直到约65 次迭代左右最优路径变化曲线才趋于最优值，且得到最优值要大于WDMGA 算法得到的最优值。此外，从表7 中两种算法的统计数据中也能够分析出，WDMGA 算法在对景德镇陶瓷文化景区旅游路线规划时，需要的时间更短、规划的效率更快，并且规划出的路径更加符合实际情况，这也表明了本文所提出算法的有效性和合理性，能够较好地应用于景德镇陶瓷文化景区的路线规划过程，为游客的旅游路径规划提供合理的线路优化设计。

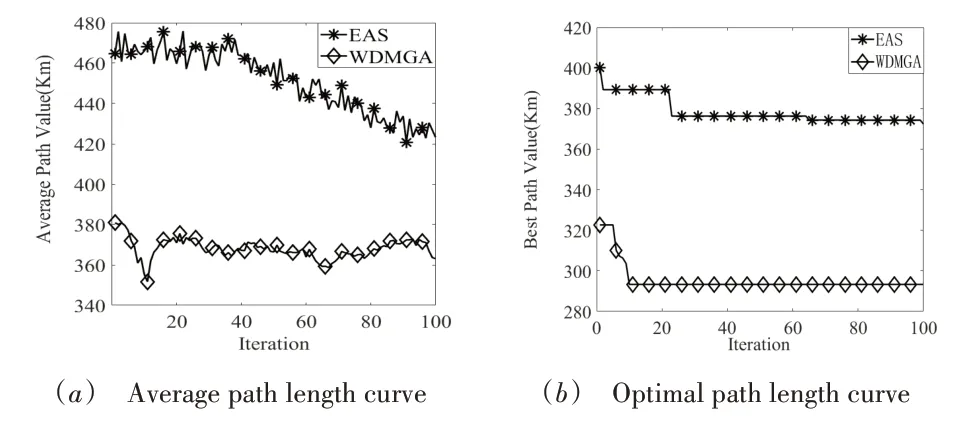
Fig.7 Variation curves of average and optimal path lengths图7 平均和最优路径长度变化曲线

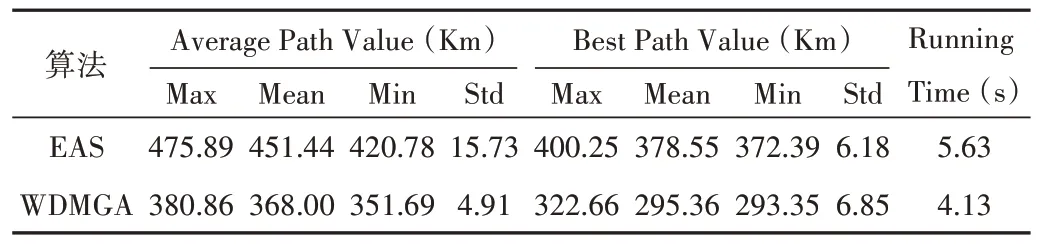
Table 7 Average and optimal path index statistics表7 平均和最优路径指标统计数据

4 结语

WDMGA 算法是在遗传算法基础上提出的一种带权重扰动机制的旅游路径规划算法。该算法在设计评价函数时将影响景德镇陶瓷文化景区分布和游览的因素融入其中，形成权重扰动因子，同时在遗传操作过程中，设计模拟退火交叉和变异算子，加快算法的寻优搜索效率，在增强种群中最优个体脱颖而出的同时，也能较好地平衡不同路况环境中接近全局最优个体的次优个体的多样性。仿真实验表明，所提出的旅游路线规划算法能够更好地根据景德镇陶瓷文化景区的实际情况进行合理、有效的旅游路线规划，且规划出的路线既可以体现景德镇市的风景文化，也可以传播景德镇的陶瓷文化，进一步提高景德镇市的知名度和陶瓷文化的传承度。