基于深度自编码器的室内指纹插值与定位方法
范贵明,乐燕芬,厉天宸
(上海理工大学 光电信息与计算机工程学院,上海 200093)
0 引言
随着无线网络技术和智能设备的普及,各类基于位置服务的应用逐渐成为人们日常生活不可或缺的部分[1]。在室外区域,全球定位系统和北斗卫星导航系统能满足大多数应用的定位需求。然而,由于无线信号的传播受建筑构造、物体阻隔和人员走动等影响,无法利用卫星导航系统在室内区域实现有效定位。因此,其他信号,如Wi-Fi、RFID、ZigBee、红外线、蓝牙、惯性导航等被用于室内定位。随着无线局域网(WLAN)作为室内接入系统的广泛使用和无线通信设备的普及,基于Wi-Fi 信号的室内目标搜索、定位、导航和跟踪等服务得到了极大发展。
其中,接收信号强度(Received Signal Strength,RSS)指纹的室内定位方法由于其部署成本较低且应用灵活的优点,成为国内外学者研究的热点[2-5]。这些方法利用各接入点(Access Point,AP)或锚节点在各参考位置的RSS 信号确定定位区域的无线信号分布特性,并由此利用目标接收的RSS 信号完成位置估计。因此,基于无线信号的室内定位系统越来越获得人们的认可。
无线定位基本分为两类:一类基于测量方式,另一类基于指纹方式。基于测量方式的无线定位系统主要通过测量到达时间(Time of Arrival,TOA)、到达角度(Angle of Arrival,AOA)或到达时间差(Time Difference of Arrival,TDOA)进行位置估计[6]。然而,这些物理量不能直接被普通的无线信号接收器所测量,因此基于指纹方式的无线定位系统更具普适性[7-9]。基于指纹方式的定位系统一般采用机器学习的方法。文献[7]采用K 近邻(K Nearest Neighbors,KNN)方法,提出了基于指纹方式的无线定位系统。支持向量机(Support Vector Machine,SVM)也在文献[10]中被用来确定设备的位置。文献[11-12]分别提出利用压缩感知(Compressive Sensing,CS)分析定位信号与指纹数据库对应关系的方法。然而这些分类方法因其结果的离散性,使得系统的定位精度受到一定程度的限制。
文献[13-14]用径向基函数(Radial Basis Function,RBF)和多层感知(Multilayer Perceptron,MLP)解决无线定位问题。通过将无线信号强度输入到训练好的浅层神经网络,直接得到连续的位置坐标。此外,基于人工神经网络的定位系统可以得到比传统方法更好的结果[15]。然而针对波动的无线信号,由于浅层网络的拟合能力有限,上述文献所提出的系统均难以实现精确定位。
在诸如视觉分类[16-17]和语音识别[18]等领域,深度神经网络(Deep Neural Network,DNN)已获得了成功应用。为此,本文提出基于深度神经网络的无线定位方法:首先在离线阶段利用少量的指纹数据,通过神经网络对其他位置进行RSS 估值,实现对指纹库更高密度的重构,减小离线阶段对原指纹数据的依赖;然后,采用四层深度神经网络结构,通过特征学习的方式,从大量波动的无线信号数据中提取特征,解决定位问题。利用堆叠自编码器(Stacked Autoencoder,SAE)对网络结构进行预训练[19],并通过反向传播进行全局微调,从而使网络能够避免手工方式,自动地从指纹数据中学习到高层特征,并通过这些特征进行位置估计,得到更鲁棒的定位结果。
1 深度自编码器指纹插值与定位方法
1.1 基于深度神经网络的指纹库重构
深度神经网络内部分为输入层、隐藏层和输出层,层与层之间是全连接的,即前一层的任意一个神经元与后一层的任意一个神经元相连。基于深度神经网络的插值结构如图1 所示。在本文指纹库重构过程中,利用离线采集的指纹数据对其他位置点的RSS 信号进行估值,从而生成位置密度更高的指纹库。设整个区域内共有m个AP,布置 有n个参考 点,其位置 表示为pi=(xi,yi),i∈{1,2,…,n};在参考点pi接收的RSS 信号向量表示为Ri=(ri1,ri2,…,rim),其中rij,j∈{1,2,…,m}是参考点pi接收的来自第j个AP 的RSS 信号,其中RSS 类别数m已知。
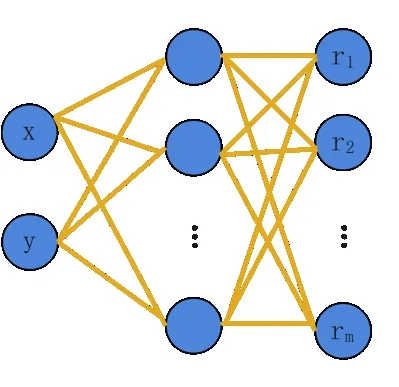
Fig.1 Structure of deep neural network图1 深度神经网络结构
在插值过程中,其位置坐标p=(x,y)作为输入,相对应的信号强度值r=[r1,r2,…,rm]作为隐藏层的输出。
模型训练好后,系统通过计算得到插值点的信号强度,即:
其中,r=[r1,r2,…,rm]为插值点的信号强度,w为深度神经网络的输出层权重,b为输出层偏置。
1.2 基于深度编码器的位置定位
自编码器是一种尽可能复现输入信号的神经网络。对接收的输入样本,经过编码将其转换成高效的抽象表示,而后经解码过程再输出原始样本的重构。算法通过调整网络参数使样本的重构误差达到最小值,从而获得输入样本的最优抽象表示。从神经网络的角度而言,编码提取的抽象表示也即网络的中间层或称隐藏层。
SAE 是将多个自编码器堆叠在一起组成的深度学习架构。输入层的数据通过第一层的自编码器后映射到第一个隐藏层;而后该隐藏层作为第二层自编码器的输入层继续进行训练获得第二个隐藏层。训练逐层进行,将前隐藏层的特征表达传递到后序的自动编码器中。调整网络中每层的参数,输出每一个隐含层的权重和偏置,从而得到输入和输出数据的模型结构[20]。隐藏层的层数在SAE中起着重要作用,它对提取特征的不变性和抽象性起着关键作用。根据文献[21],SAE 设置为5层。
如图2 所示,在本文所提算法中,输入的RSS 信号向量,通过SAE 提取的特征建立与位置坐标之间的映射模型。SAE 用梯度下降将输入输出的误差最小化,然后将SAE 训练结束的网络作为初始状态,为了有效地训练定位系统参数,本文采用Dropout 方法,并设置随机置零的概率为0.1。
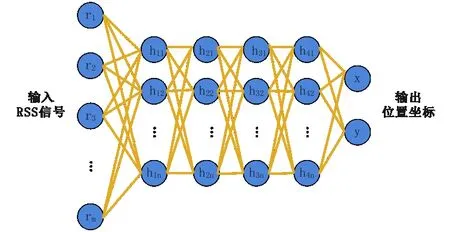
Fig. 2 Structure of deep encoder图2 深度编码器结构
输入层是由m个单元组成的,中间一层是n个单元组成的隐藏层。其中,输入层r数据集表示每个AP 的RSS 数据,即:
其中,wi是权重矩阵,bi是偏置向量,fi是激活函数,例如有Sigmoid 函数,双曲正切函数和修正线性单元函数等。该算法中采用的是Sigmoid 函数。
在线定位阶段,定位系统用已训练的深度神经网络模型,从目标的RSS 信号向量中提取特征,然后通过深度神经网络模型计算待测点的位置坐标,即p=(x,y)。
1.3 DNN-SAE算法步骤
如图3 所示,DNN-SAE 算法由指纹数据库、深度学习网络、在线采集信号和定位位置预测等部分组成。大致分为离线阶段和在线阶段两个部分。具体算法步骤如下:
Step1:在室内环境中采集的RSS 信号组成深度学习的原始训练集。
Step2:利用深度神经网络对其他位置的RSS 信号进行估值,最终完成指纹数据库重构。
Step3:将重构的指纹数据库输入到SAE 中进行预训练,逐层对RSS样本编码,提取特征数据。
Step4:通过SAE 提取的特征建立与位置坐标之间的映射模型。
Step5:逐层训练并调整网络参数,用梯度下降将输入输出的误差最小化,训练结束后得到关于RSS 信号与位置坐标的室内定位模型。
Step6:在线阶段,利用训练好的模型,从采集的RSS 信号提取有效特征,计算出所对应的位置坐标。

Fig.3 Block diagram of positioning algorithm of deep autoencoder图3 深度自编码器定位算法框图结构
2 实验结果与分析训练
为验证本文所提出的基于深度自编码器的室内指纹插值和定位方法性能,在两个不同的场景进行实验,分别基于米什科尔茨大学提供的公共数据集[22]的房间区域类定位和基于自主采集的办公环境数据集的精确定位类,以验证本文所提方法的可行性和有效性。
2.1 实验环境
数据集1 是米什科尔茨大学提供的公共数据集。该数据集采用ILONA 系统对一个三层办公大楼进行了数据采集和记录。测量位置遵循建筑上的网格布局,采样点的间隔为1m。数据集1 采用了该公共数据集在1 楼采集的Wi-Fi 信号,实验环境如图4 所示,图中的颜色和线条用于分隔区域。这个数据集共分为6 个房间,当对目标进行区域类定位时,则需正确判定目标所在的房间号。

Fig.4 Experimental layout of dataset 1图4 数据集1的实验布局
数据集2是在光电学院大楼面积约为70m×14m 的8楼环境中进行采集。实验环境具体布局如图5 所示,其中黑点为参考位置点,红块表示在线测试点(彩图扫OSID 码可见)。实验中,利用移动智能终端搭载自主开发的微信小程序在多个工作日扫描采集参考点和测试点的Wi-Fi 信号强度和在线RSS 信号,将目标未能接收到信号的AP 的RSS值设为0。两个实验场景的参数如表1所示。
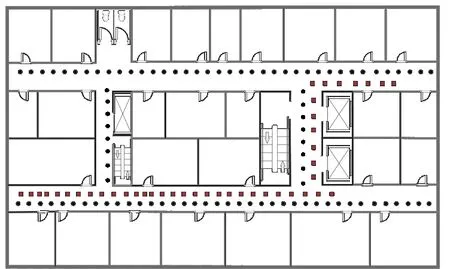
Fig.5 Indoor office map of dataset 2图5 数据集2的室内办公地图

Table 1 Experimental parameter settings表1 实验参数设置
2.2 定位空间内RSS估值结果分析
首先,对深度神经网络定位空间内的RSS 估值结果进行实验分析。从数据集1 中随机抽取1stFloorLobby 中的101 个采样点作为原指纹数据,分别采用深度神经网络(DNN),距离加权反比例插值法(Inverse Distance Weight,IDW)和普通克里金算法(Kriging)对其余50 个待测点作RSS 估值;同样从数据集2 中随机选取区域内92 个采样点的RSS 作为原指纹数据,用上述3 种算法对其余42 个待测点作RSS 估值,并对算法获得的估计值与实测值进行对比。图6(a)和(b)分别给出了在两个数据集上的实验结果。估值误差是每个采样点用算法估计的各AP 的RSS 值与实测值绝对误差的平均值。
从图6(a)和(b)可以看出,在数据集1 中DNN 的RSS估值误差(估值点的估计值与实际值取绝对值作差,再取平均)整体低于IDW 和Kriging,其中有2 个位置点的误差达到25dB 左右,最低在3dB 左右;而在数据集2 中,DNN 的误差最高在16dB 左右,最低在3dB 左右,从两个数据集中都能得出DNN 优于IDW 和Kriging。
2.3 区域类定位性能分析
区域定位,也即实现目标房间级精度的定位。实验中采用数据集1 进行了多次实验以评估本文所提指纹重构算法和定位算法的性能。
实验中,首先分析不同数量的指纹数据训练SAE 对定位精度的影响。在每个房间随机选择10%的指纹作为训练数据,随后逐步增加训练数据量,另从指纹库中随机选择了44个测试点进行位置估计。实验结果如图7所示。
图中定位成功率指对目标估计的所在房间号与其实际房间号一致。从图7 中可观察到,随着训练数据的增加,不管是SAE 还是WKNN 算法,定位成功率都逐步提高。SAE 从81%提高到92%,WKNN 从80.5%提高到86%。
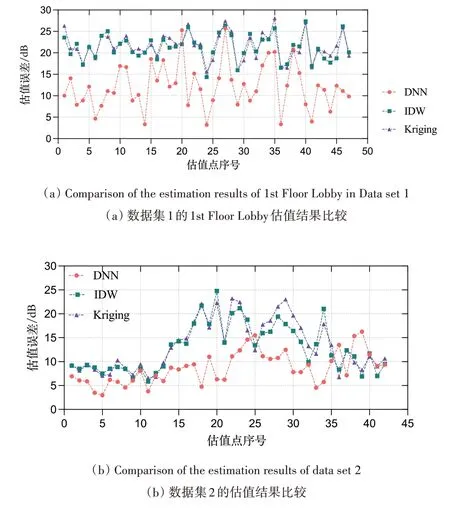
Fig.6 Comparison of the estimation results图6 估值结果比较

Fig.7 Positioning success rate for every additional 50 training data图7 每增加50个训练数据的定位成功率
接着分析在少量指纹数据的情况下,如何通过插值提升定位性能。实验中,在每个房间中随机选取10%的指纹数据,并传给深度神经网络对其他位置点进行RSS 信号估值以重构高密度的指纹库。从图8 可以看出,仅使用44 个指纹数据时,本文所提算法的定位成功率约为83%,而WKNN 在80.5%左右。随着新生成指纹数据的加入,算法的定位性能得到提高。在增加了200 个新生成得到的数据时,SAE 定位性能约为89%,WKNN 在85%左右。
2.4 精确定位结果分析
在数据集2 中,利用所提算法对42 个在线测试点进行实时定位,并与其真实位置进行比较,获得定位误差作为算法性能指标。考虑到监测区域内AP 点的数量较大,且楼层内狭长走廊的布局,使得某些AP 的信号较微弱,或者覆盖范围较小,因此实验中根据每个AP 被检测到的RSS信号强度之和以及每个AP 被检测到的次数分别筛选AP,筛选结构如表2所示。
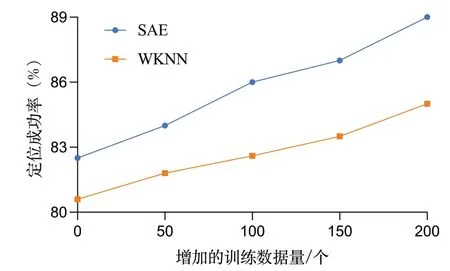
Fig.8 Positioning success rate for every 50 additional newly generated data图8 每增加50个新生成数据的定位成功率

Table 2 AP screening results in data set 2表2 数据集2中AP筛选结果
采用两种准则筛选AP 后的定位结果如图9、图10 所示。图9 中筛选AP 强度之和大于300(108 个AP)的精度最好,SAE 算法的平均定位误差为1.61m,WKNN 在2.26m,定位精度提高29%。而图10 中筛选AP 被收到次数大于3个(144 个AP)的精度最好,SAE 的定位精度在1.6m,WKNN 在2.31m。从图中也可观察到,当AP 数量足够多时,继续增加AP,算法性能并不会有大的提升。
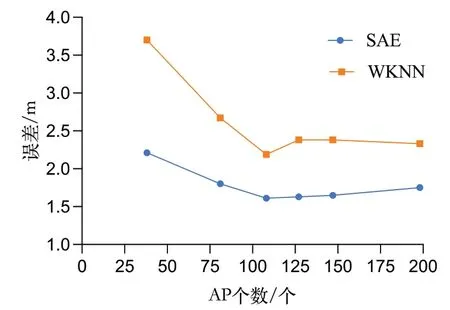
Fig.9 Positioning error obtained by filtering the number of APs based on the sum of AP intensity图9 基于AP强度之和筛选AP得到的定位误差
为了进一步验证算法的定位性能,图11 给出了数据集2 中本文所提算法、WKNN 算法的定位误差累计分布函数。在本实验中,在原有的92 个离线指纹库中,加入15 个由深度神经网络生成的新指纹。由误差累计分布曲线可观察到,整体曲线表明本算法在抑制大误差和提高平均定位误差的性能上均优于其他3 种方法。具体而言,上述4种算法在数据集2 中的平均定位误差分别是1.49m、2.18m、1.75m 和2.33m,与WKNN 算法相比,该算法定位精度提高约36.1%。
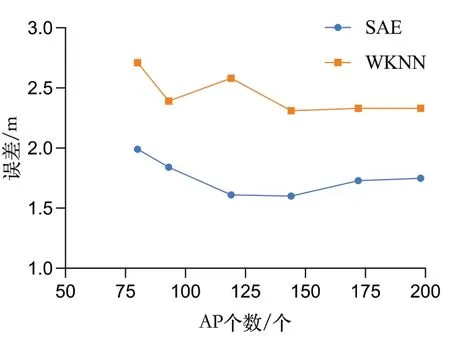
Fig.10 Error obtained by screening the number of APs based on the detection time of AP图10 基于AP被检测的次数筛选AP个数得到的误差

Fig.11 Comparison of positioning performance of different methods图11 不同算法的定位性能比较
3 结语
本文提出了一种基于深度自动编码器的离线指纹重构和室内定位方法。通过公共数据集和实际办公环境收集数据实验,对所提算法在区域类定位和精度定位中的性能进行了验证和分析。实验结果表明,更多的指纹训练数据可以提高算法定位精度。而使用更多新生成的指纹数据,有利于节省构建指纹库的时间和成本。通过与现有一些定位算法比较,在采用同样数量的指纹数据时,通过深度神经网络重构的高密度指纹库和堆叠式自编码器的定位模型,该算法在区域类定位中有利于定位成功率提升,在精确定位中则能有效降低定位误差。

