基于威布尔分布的新能源汽车驱动电机可靠性分析
王道成,李唯真
(长安大学 汽车学院,陕西 西安 710064)
随着我国新能源汽车行业的快速发展,混合动力汽车、燃料电池汽车、纯电动汽车等新能源汽车所占市场份额不断增加,新能源汽车相关可靠性问题逐渐成为研究热点[1-2]。
驱动电机作为新能源汽车的一个重要总成,其能否长时间可靠工作对新能源汽车的安全性、经济性和动力性具有重要影响[3]。针对新能源汽车驱动电机的可靠性分析方法,目前国内外学者研究方法可主要分为基于故障数据的可靠性分析和基于故障物理的可靠性分析方法[4-8]。SHU[6]基于电机控制器中各组件的故障率,分析各部件电机控制器的可靠性指标对电动汽车使用寿命的影响趋势,从而发现薄弱环节,有利于对驱动电机做进一步设计和维护。严婷婷[7]基于电机失效模式,分析电机失效对电机性能的影响,并以此建立了相关可靠性分析模型。陈诗怡[8]针对某驱动电机典型失效模式,基于驱动电机故障物理方法,进行多失效模式的可靠性建模,并以此进行可靠性分析和相关优化设计。
由于受试验时间和人力、物力成本的影响,驱动电机试验寿命数据通常具有小样本量的特点,增加其分布类型参数估计的难度。为此,本文针对具有小样本量特点的驱动电机故障时间数据,利用灰色模型GM(1,1)进行灰生成,充分挖掘数据信息,对驱动电机故障数据进行三参数威布尔分布参数估计,并根据参数估计结果完成驱动电机寿命可靠性分析。
1 可靠性分析流程
针对完全故障样本的驱动电机试验寿命数据的可靠性分析流程如图1 所示。
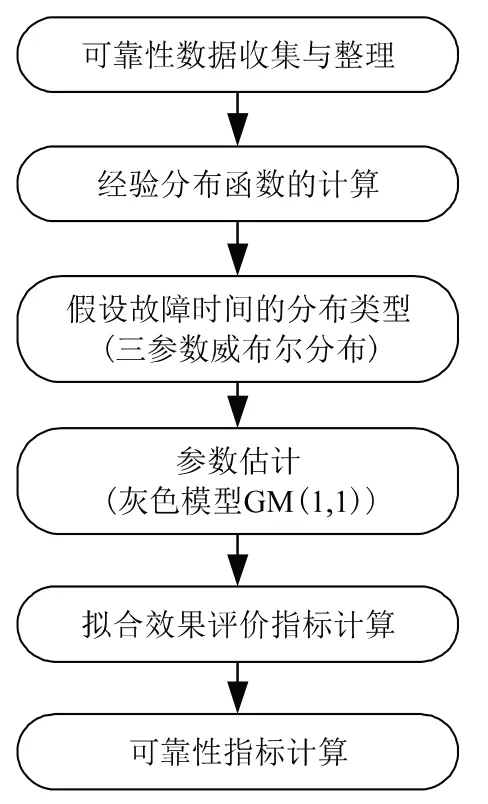
图1 可靠性分析流程
1)可靠性数据收集与整理:整理驱动电机故障时间数据,并按其数值大小进行升序排序。
2)经验分布函数计算:判断驱动电机故障时间数据数量,采用相应的计算公式计算其经验分布函数。
3)假设样本的分布类型:本文采用三参数威布尔分布模型。
4)参数估计:对原始故障时间序列作灰生成,建立灰色模型GM(1,1),完成位置参数、尺度参数和形状参数的参数估计。
5)拟合效果评价指标计算:本文采用均方根误差(Root Mean Square Error, RMSE)和相对均方根误差(Normalized Root Mean Square Error,NRMSE)对样本数据的拟合效果进行评价。
6)可靠性指标计算:主要为驱动电机平均寿命。
2 理论算法模型
2.1 经验分布函数计算模型
故障样本对应的经验分布函数计算,是进行分布类型参数估计和可靠性分析的前提和基础。当样本量较大时,可直接采用经验分布函数定义公式计算,而对于小样本量完全故障样本,直接采用经验分布函数定义公式计算时,会产生较大的误差。为此,常采用海森公式、数学期望公式和近似中位秩公式等,其中,如式(1)所示的近似中位秩公式最为常用。
式中,i为失效样本的序号;n为样本总量;Fn(ti)为第i个失效样本对应的经验分布函数。
2.2 三参数威布尔分布模型
在威布尔分布研究方面[9-13],三参数威布尔分布相比于两参数威布尔分布,引入了位置参数,更能充分和灵活地描述数据分布规律,因此,也广泛应用于各领域故障数据可靠性分析工作中,但位置参数的引入也同时加重了参数估计的复杂程度。三参数威布尔分布的分布函数F(t)、概率密度函数f(t)和可靠度函数R(t)分别为
式中,γ为位置参数;m为形状参数;δ为尺度参数。
2.3 基于灰色模型 GM(1,1)的三参数威布尔分布参数估计方法
针对威布尔分布模型,常见的参数估计方法有相关系数优化法、矩法、回归估计法和灰色估计法。其中,灰色模型GM(1,1)在分析小样本量数据时,具良好的参数估计性能。参考文献[14]中提出的三参数威布尔分布参数估计方法,通过求解反函数可将式(2)中的F(t)变换为
若t1,t2,…,tn是所有样本按照升序排序的故障时间,则Fn(ti)是各样本故障时间按照式(1)计算得到的对应的经验分布函数,对于式(5)令:
将式(6)中的xi代入到式(5)可得:
此时,式(8)与灰色模型GM(1,1)的时间响应函数的关系为
式中,a,b为待估参数。采用最小二乘估计方法的思路,令:
则三参数威布尔分布中位置参数γ和形状参数m的估计结果为
同理,对于三参数威布尔分布中的尺度参数δ,令:
则最小二乘估计结果为
此时,三参数威布尔分布中尺度参数δ的估计结果为
2.4 参数估计效果评价
在分布类型参数估计效果评价指标方面,如式(19)和式(20)所示,均方根误差RMSE 和相对均方根误差NRMSE 都可以对参数估计结果进行较好的衡量,均方根误差RMSE 和相对均方根误差NRMSE 越小,表明参数估计效果越好。
式中,Fn(ti)为根据参数估计结果计算得出ti经验分布函数。
3 案例应用
如表1 所示,为某型号驱动电机的试验故障时间数据,其中的经验分布函数采用式(1)所示的近似中位秩公式求得。
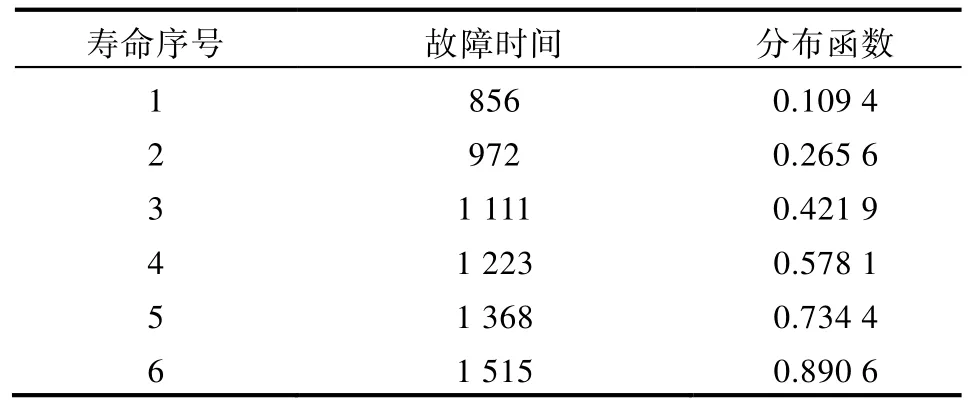
表1 驱动电机故障时间信息
利用前述三参数威布尔分布参数估计计算方法,得出过程矩阵B、Y和M的计算结果为
从而得到位置参数γ、形状参数m和尺度参数δ的估计结果分别为γ=414.407 0、m=3.074 5、δ=862.000 6。
此时,该型号批次驱动电机试验故障时间数据三参数威布尔分布参数估计结果分别如图2 和图3 所示。
根据估计结果,计算均方根误差RMSE 和相对均方根误差NRMSE 的数值为0.018 99 和0.033 51。
结合均方根误差、相对均方根误差和图2、图3 所示的驱动电机故障概率分布函数估计结果和故障概率密度函数估计结果,可以看出三参数威布尔分布估计结果与原始数据拟合效果较好,可有效描述驱动电机故障时间分布趋势。最终可得到该型号批次驱动电机的平均试验寿命θ为
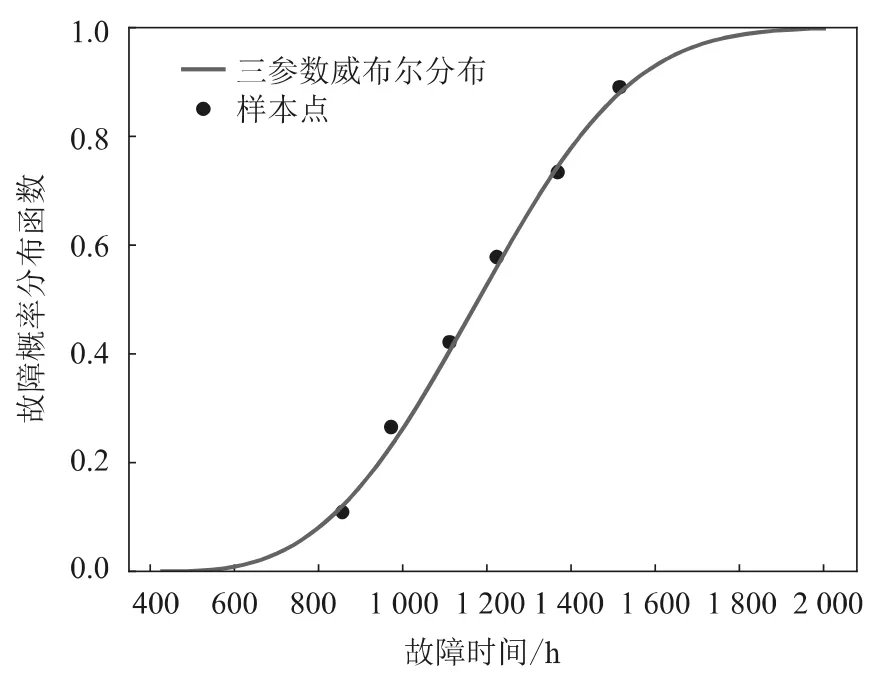
图2 故障概率分布函数估计结果

图3 故障概率密度函数估计结果
4 结论
本文在完全故障样本数据可靠性分析体系的基础上,利用灰色模型GM(1,1)对某型号驱动电机小样本量实验故障数据建立三参数威布尔分布模型并完成相关可靠性分析,得出其平均故障寿命θ为1 185.005 7 h。同时,误差分析结果表明,三参数威布尔分布模型的拟合精度高,可靠性评估结果也可进一步支撑驱动电机后续使用维护,保证产品质量。

