基于GeoGebra数学实验的在线题组测试*

福建省福州高级中学(350007) 赖晓晖

“互联网+”教育为个性化学习带来便利.目前的高中数学在线学习,通常是文本、视频讲解为主,辅之以在线答疑.高中数学教学中经常遇到含参数的动态图形问题,动态图形问题常是教学难点.在线学习中,学生只能看视频中教师的演示过程,无法亲自动手参与实验,重复看视频录像,也只是重复看同一个演示过程,还有没有其他可能呢?学生无法确认.这样还是不能很好地突破难点.如果学生能动手操作数学实验,“经历直观感知、操作确认,猜想验证”[1],升华到思辨论证,可以较好地建构知识体系.笔者尝试将在线测试与GeoGebra数学实验融合,获得了较好的教学效果.

1 GeoGebra数学实验

GeoGebra是一款集作图、运算、交互为一体的功能强大的数学软件.GeoGebra是基于JavaScript编写的开源软件,用GeoGebra制作的实验课件很适合于在线呈现与操作.它可用绘图工具、指令、脚本编程完成作图,制作的数学实验的交互功能很好.“点、线、面、几何体都是GeoGebra的对象,通过属性设置或编写脚本,可以个性化地设置、改变对象的属性[2].”在GeoGebra官网,可以在线制作数学实验,也可以在本机上制作数学实验课件,再生成在线实验.

2 在线题组测试

GeoGebra官网提供了“活动”页面,“活动”可以将GeoGebra课件、单项/多项选择、图片、文字符号、文件、视频、链接集中在一个页面.利用这个页面,笔者设计出基于GeoGebra数学实验的在线题组测试.“活动”可以应用为“课程”,在线学习的学生进入课程后,就可以进行在线测试和在线探究实验,教师可以在线查看测试的实时结果,明了每个学生每道题答题的正确与错误,知晓每位学生测试的实时进度.

数学题组可以围绕某一类知识,采用题目训练的方式,让学生针对该类知识和相关问题进行练习,以达到对该类知识的充分理解和在具体的问题情境中活学活用,从而让学生在针对某类知识的题目中找寻规律,发现题组中蕴含的知识和解题技巧[3].这一类知识,可以是一个微专题,甚至更小的一个知识块,通过设计有内在逻辑关系的数学题组来揭示问题的基本原理、进行变式训练.设计数学题组要求由浅入深、层层递进,引导学生积极思考、主动探究,进而突破难点、掌握规律、理解问题本质.

在实验探究过程中,无论是二维图形,还是三维图像,GeoGebra都能直观地呈现动态变化图像,学生可以通过在线操作数学实验,观察由参数变化引起的观测量的具体变化,还可以用GeoGebra 度量、计算某个量,从而验证或否定自己的疑问或猜想,或者在观察变化情况后主动探求规律.这些都有利于提升学生在线学习的兴趣和效果.

教师通过在线题组测试结果可以了解每个学生完成题组情况(如图1 图2),准确了解教学目标达成情况,适当调整线上或线下的教学进度.

图1 学生完成测试的进展

图2 各选项选择的人数

3 在线题组测试的结构

经过多次实践、总结,笔者认为探究性的在线测试的构成可以是:

(1)引言: 对即将探究的问题作概要描述,还可以对核心知识点作解析;

(2)测试1: 对很基础的内容进行测试,也就是后续学习中需要掌握的内容;

(3)测试2: 该在线题组希望解决的问题,难度高于测试1,也是本题组和实验探究要突破的问题;

(4)GeoGebra 数学实验1: 以测试2 为基础制作的数学实验,学生可以动手操作,这个实验可以包括后面的测试将涉及的实验;

(5)视频/文字讲解、小结: 讲解测试2;

(6)测试3: 与测试2 难度相当的变式问题;

(7)测试4: 比测试2 难度相当或稍大的变式问题;

(8)GeoGebra 数学实验2: 如果GeoGebra 数学实验1 不能涵盖测试3 和4,可以增加一个或两个数学实验;

(9)视频/文字讲解、小结: 对测试3、4 解答、小结,甚至提出新问题给学生思考.

通过有梯度、递进的题组的引导及动手实验,学生专注于某一小类问题的探究与实验, 题组将学生思维引向深入,有梯度的题组能降低问题解决的门槛,让学生感到对学习解决这类问题有信心、能上手,递进式题组带给学生成功的体验,有成就感.一大类问题可以设置多个题组,小步子递进,能让一部分学生感到学有所得,又能提升学生的问题意识、引导学生思考,让学生感到还有更深入的问题可以探究.

实验探究除了帮助学生解答疑问、理解问题,将带给学生更多启发和思考.自己提出问题并尝试自己解决问题是GeoGebra 数学实验探究的目标.能提出问题是学生的思维充满活力的表现.应当鼓励学生对问题大胆猜想,并借助于适当的工具(如: GeoGebra 数学实验)验证自己的猜想是否正确.这是学生学会研究的必经之路,也是培养学生创新意识的有效途径.

GeoGebra 数学实验将抽象问题可视化, 学生在思考问题之后,能用直观图形帮助理解,利于直观想象素养的提升.“如果要用一句话描述数学教育的根本,那就是培养学生的数学直观,因为数学的结论是‘看’出来的,不是‘证’出来的,依赖的是数学直观,这是‘三会’的现实表现.数学直观是一个人长期进行数学思维形成的,是逐渐养成的一种思维习惯.这个思维习惯日积月累就形成了数学素养[4].”

笔者认为,按上述结构,基于GeoGebra 数学实验的在线题组测试可以实现在线测试与实验探究的相互融合.

4 在线题组测试举例

活动1球与正方体的截切问题

问题1已知正方体ABCD-A1B1C1D1的棱长为1,则以该正方体的中心O为球心,当球O与正方体外接时,球半径为( )

问题2已知正方体ABCD-A1B1C1D1的棱长为1,则以该正方体的中心O为球心,当球O与正方体的12 条棱相切时,球O与正方体的交线长为( )

A.6πB.C.D.12π

数学实验1: 小球的球心是正方体ABCD-A1B1C1D1的中心O,当球半径变化时,请观察球与正方体的位置关系.特别注意三种位置关系: 球与正方体内切、球与正方体的棱相切、球与正方体外接.

问题3以D为球心,半径为1 的球D与棱长为1 的正方体ABCD-A1B1C1D1相交,则球D与正方体的交线长为( )

A.2πB.C.πD.

问题4以D为球心,半径为的球D与棱长为1 的正方体ABCD-A1B1C1D1相交,则球D与正方体的交线长为( )

A.2πB.C.D.

数学实验2: 小球的球心是正方体ABCD-A1B1C1D1的顶点D, 当球半径变化时, 请观察球与正方体的位置关系.注意球半径r在下列情况下的交线:r ＜1、r= 1、

活动1 的题组比较侧重于对球与正方体位置关系的判断,四个问题可以使用同一个数学实验完成探究,数学实验1截图如图3,数学实验2 当时截图如图4.所以在视频、文字的解析中,结合动态图像、截图,告诉学生球半径等于多少的时候,符合题目所述的情形.问题4(如图5)有一定难度,也是下一个题组要解决的问题.

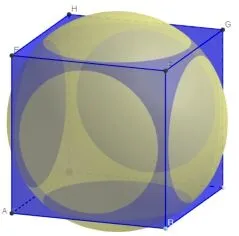
图3

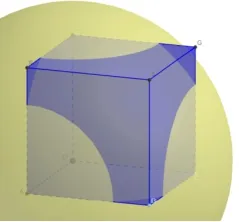
图4

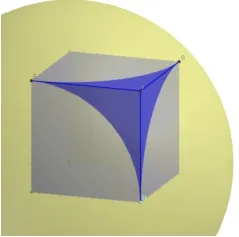
图5

活动2与球相关的交线长度问题

问题1已知正方体ABCD-A1B1C1D1的棱长为2,则以该正方体的中心O为球心,若正方体的面ABCD截球O所得圆O1与正方形ABCD内切,则球半径为( )

问题2已知正方体ABCD-A1B1C1D1的棱长为2,则以该正方体的中心O为球心,为半径的球与正方体的表面的交线长为( )

A.0 B.2πC.4πD.6π

数学实验1: 以该正方体的中心O为球心,半径在变化的小球,当半径变化时,请观察球与正方体的棱相切到外接的交线的变化,可以通过按钮改变观察的视角.

问题3已知正方体ABCD-A1B1C1D1的棱长为2,则以该正方体的面ABCD的中心M为球心,为半径的球与正方体的表面的交线长为( )

问题4已知正方体ABCD-A1B1C1D1的棱长为2,球O与该正方体的各个面相切,则平面ACB1截此球的截面的面积为( )

数学实验2: 小球以正方体的顶点D为球心,当球D的半径变化时,请观察球与正方体交线的变化.(如图10)

图10

问题2 的直观图和正视图截图如图6、7,学生可以通过设置的按钮控制视角,便于全方位观察几何图形.通过直观图和正视图的对比观察,学生容易理解这个问题.数学实验1是解决问题2 所需要的数学实验,和上一个活动的实验1 类似,但观察要求不一样.

图6

问题3 的截图如图8,要求学生在实验操作及视频讲解后基本掌握截面问题.问题4 的截图如图9,球心到截面的距离d的计算稍有变化,可以加深了R2=r2+d2的理解.

图8

图9

经过两个题组的训练、四个数学实验的操作验证,学生对球与正方体的截面问题会有个较全面、深刻的认识.在每个题组中,问题与数学实验紧密相关、相互支撑.题组与数学实验设计的目标是: 学生通过实验操作、直观想象、逻辑推理和数学运算,适当迁移,能够理解、掌握一类数学问题的数学本质.

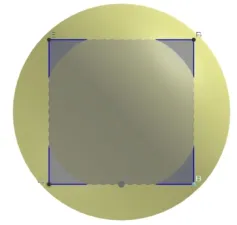
图7

5 结语

通过有限的几道题, 引导学生解决一小类问题.通过有限个在线数学实验, 引导学生研究问题、增长素养.基于GeoGebra 数学实验的在线题组测试让在线学习也可以有不小的收获.