以数学史带动学生内驱力,为课堂思政添砖加瓦*
——以“数系的扩充和复数的概念”为例
长江大学信息与数学学院学科(434023) 孙 浩 刘彩云
1 引言
美国著名的教育心理学家奥苏贝尔提出:“内驱力是指学生学习的社会性需求.这种需求一旦产生,学生便对学习表现出一定程度的兴趣、主动积极的情感态度、良好的注意和克服困难的意志努力, 从而发动并维持学习行为的进行,使其积极投入到学习活动中去.”简言之,内驱力就是内部动力,也就是动机.因此要想学生主动投入到数学学习中,就要采取各种有效措施激发学生内驱力.法国数学家亨利·庞加莱曾说:“如果我们想要预测数学的未来,那么适当的途径是研究这门学科的历史和现状.”[1]毫无疑问,数学的跌宕发展历史可以吸引学生,激发学生的好奇心,使其产生积极主动的态度.
课程思政主要形式是将思想政治教育元素融入到各门课程中去,潜移默化地对学生的思想意识、行为举止产生影响.课程思政首先展现的是一种科学思维;其次是创新思维,在课程思政建设的过程中,也需要创新思维来实现课程思政的创新发展.[2]目前全国盛行课程思政,可以以数学史为载体进行课堂思政,从新的方向探索课堂思政的途径,使课堂思政蓬勃发展.
本文以人教版高中数学必修二第七章第一节“数系的扩充和复数的概念”为例,探讨如何在课堂中用数学史带动学生内驱力,如何用数学史丰富课堂思政.
2 教学设计与实施
2.1 情境引入
师: 同学们,大家好.很高兴和大家共同学习必修二第七章第一节的有关内容,数系的扩充和复数的概念.首先请同学们跟随老师回顾一下我们从小到大的数是如何产生的.数这一概念源于事物个数的表示,在社会发展中,逐步学会了以对应的方法来表示事物的个数,如“屈指”计数,“结绳”计数、“堆石子”计数等,然后人们从计数过程中抽象出数字0、1、2、3、4......并将它们称为自然数.接着是哪个数产生了呢?
生: 随着生产生活的发展,人们意识到仅用数量表示一个事物是不全面的,还应加上表示方向的符号,因此为了表示相反意义的量,负数产生了.
师: 是的,看来同学们对数的历史发展都有一定的了解.渐渐地,人们发现仅仅有整数是不够的,例如在等额分配问题中,三个人分两个苹果,每个人应分得多少呢? 该结果无法用整数表示,于是......
生: 分数出现了!
师: 没错.早在五百年前,毕达哥拉斯学派的优秀弟子发现在边长为1 的正方形中,其对角线长无法用整数之比,也就是无法用有理数来表示,他的这一发现使无理数第一次出现在人们面前,而且求得边长为1 的正方形的对角线长引发了第一次数学危机, 同学们有兴趣可以课后了解一下.现在相信每一位同学都可以灵活的运用根号进行无理数的相关运算,但同学们知道吗? 从公元前500年无理数的第一次发现,到17 世纪法国数学家笛卡尔引入根号这一符号再到19 世纪无理数体系的完全确立,整整经历了2300 多年.
生: 原来数学史的发展这么曲折,我们现在学习的一个小知识都可能是数学家们经历上百年近千年创造发现的.
师: 是啊,这是一个长期且艰难的过程.那么总结一下数系的扩充过程是怎样的呢?
生: 由自然数系扩充到整数系,再扩充到有理数系,最后扩充到实数系.
师: 很好,我们也可以用Venn 图进行表示.其实数系的扩充中有两个字一直推动着数系的发展,那就是运算.在自然数集中,加乘封闭;接着引入整数是我们减法的需要;在有理数集中可以进行加减乘除;在实数集中运算就已经完备了.那同学们有没有发现在运算过程中什么是一直不变的呢?
生: 是运算律.
师: 对,在数系扩充过程中运算律是保持不变的,这也是数系扩充的一大特点.同学们还能不能发现其他的特点呢?
生: 老师,我发现扩充后的数集仍然包括原来的数集.
师: 很好,这样我们就总结出了数系扩充的两大特点.
生: 老师,数系扩充到实数就结束了吗? 还能不能继续扩充呢?
师: 同学们提出的这个问题很有价值,很多数学家们之所以成为数学家,其原因就在于他们能勤于思考,勤于提问题,勤于发现数学中不完备的地方,勤于探究数学的新领域.大家想知道数系能否继续扩充,咱们先看这样一个问题.
设计意图课堂开始带领同学们回顾数的发展历史,既可以让学生感受数学发展的艰辛历程,又可以让学生融入数学史,激发学生内驱力;同时通过启发学生,让学生站在数学家的角度提出问题,推动课堂进展.
2.2 探究新知
师: 有没有两个数和为10,积为40 呢?
生: 设这两个数分别为x,y,可得方程即x2-10x+4=0,Δ<0,所以无解.
师: 看来同学们都是用咱们学过的知识求得无解.其实这个问题是1545年,意大利数学家、物理学家、医学家卡尔达诺(又称卡丹、卡尔丹)在他的《重要的艺术》一书中提出的,但是卡尔达诺并不是求得无解,而是得到结果为和
(学生疑惑)
师: 其实当时的卡尔达诺也像同学们一样疑惑,负数怎么能开根号呢? 但是咱们先抛开疑惑算一下这两个数的和是否为10,积是否为40 呢?
师: 没错,可以说卡尔达诺是受着良心的谴责写出了这两个在当时并不被人们接受的数,他虽然是历史上第一个把负数平方根写进公式中的数学家,但是他并不承认它的存在,卡尔达诺心想这数太诡异了,所以称它为“诡辩式的数”,也因此与数学的一大发现失之交臂.
生: 那太遗憾了,老师,我相信肯定还有其他数学家继续研究负数平方根.
师: 是的,1572年,意大利数学家拉斐尔·邦贝利在他的《代数》一书中讨论了三次方程的根,他首先利用因式分解求解方程x3+15x+4=0,得到三个实数解为这是在当时看起来很正常的三个实数解;但是这个方程并没有这样结束,而是邦贝利又用卡尔达诺发明的用于解一元三次方程的卡尔达诺公式求解了一下,卡尔达诺公式就是对形如x3+px+q= 0(p >0,q >0)方程求解的其中一个求根公式:那么利用求根公式求出来的其中一个解是什么呢?
师: 没错,那它对应通过因式分解求出来的三个根中的哪个呢?
生: 好像都不是,是卡尔达诺公式出错了吗?
细胞胞浆可见的棕黄色颗粒为β-catenin蛋白的阳性表达,棕黄色颗粒越多,表达越明显。高脂造模后,模型组中β-catenin蛋白表达明显高于正常组(P<0.01);与模型组相比,三种药物均能降低β-catenin ,Wnt抑制剂WIF降低作用较强(P<0.01),护心康组和阿托伐他汀组也有明显的降低作用(P<0.05);WIF降低β-catenin的作用较阿托伐他汀强(P<0.05),图2、表2。
师: 当时邦贝利也和同学们有相同的疑问,他多次检查公式并计算,发现这个结果是正确的,他想这个结果是两项相加,还能不能继续化简呢? 这两项的区别是什么呢?
生: 只相差一个符号.
(学生思考)
设计意图以数学史中的数学问题等为线索,以具体的数学史情境为背景,让学生走进数学史,以数学家的角度发现问题、提出问题、解决问题,一改直接教授知识的课堂,利用数学史激发学生的好奇心,使学生产生认知冲突,从而主动积极探究,烘托了课堂气氛.
2.3 新知构建,例题讲解
师: 不知道同学们心中是否有了自己的解决方法.为了解决负数开平方问题,我们可设想引入一个新数i,并规定:i2=-1 且实数可以与i 进行四则运算,运算时满足加、乘的运算律(交换、结合、分配律),这个i 最早是在1777年,欧拉首次提出的,我们称之为虚数单位[3].
生: 为什么用i 这个字母而不用其他的呢?
师: i 是取自笛卡尔创立的虚数imaginary 一词的首字母,原义是它只存在于虚幻之中,这样同学们就能更加清晰地记住这个字母了.实数可以与i 进行四则运算,实数a与i 相加可以写为...
师: 实数a与i 相乘可以写为...
生:bi.
师: 实数a和实数b与i 的积相加,结果记作...
生:a+bi.
师: 很好,那同学们思考并小组讨论能否用一个统一的形式来表示这些结果呢?
(小组讨论)
生: 可以用a+bi 表示.
师: 同学们的思维都非常活跃,但是这个结果是不是缺少什么东西呢?a和b有没有范围呢?
生:a,b ∈R.
师: 对,那么这个统一的形式或者说这个新数,我们就写为a+bi(a,b ∈R).其实从虚数单位的引入到新数系的完全确立,其中经历了200 多年,一个新数系想要确立的最大难点在于突破人们的认知障碍,随着虚数单位的引入、新数a+bi(a,b ∈R)的构造,为了确定新数系,我们还应该确定哪些相关概念呢? 带着这个问题我们将进行接下来的学习.
首先是复数的有关概念: 形如a+bi(a,b ∈R)的数叫做复数,通常用字母z表示,即z=a+bi(a,b ∈R),这一表达形式叫做复数的代数形式,其中a叫做复数的实部,b叫做复数的虚部;全体复数所形成的集合叫做复数集,一般用C表示,即C={a+bi|a,b ∈R}[4].
例1写出复数
的实部和虚部(学生回答).
师: 在之前学实数的过程中,确定完实数概念后对实数进行了一系列分类,同学们能否类比实数的分类对复数的分类提出自己的想法呢?
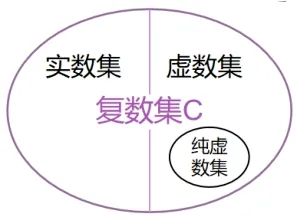
师: 从Venn 图中可以看出实数集是复数集的什么呢?
生: 子集.
师: 具体来说是...
生: 真子集.
例2说明这些数中,哪些是实数,哪些是虚数,哪些是纯虚数? (学生回答)
师: 由刚刚学习的概念,我们不难发现一个复数其实是由它的实部、虚部共同决定的,如果我们在复数集中任取两个复数,如何判断这两个复数是否相等呢?
在复数集C={a+bi| a,b ∈R}中任取两个数a+bi,c+di(a,b,c,d ∈R),我们规定:a+bi=c+di ⇔a=c且b=d.
生: 也就是如果两个复数相等,则这两个复数的实部对应相等,虚部对应相等.
师: 很好,那两个复数能比较大小吗?
生: 虚数带i 怎么比较大小呢?
师: 复数带i 是无法比较大小的,只有两个复数都为实数时才能比较大小,虚数和实数、虚数和虚数之间不能比较大小.
例3若4+bi=a-2i,求实数a,b的值(学生回答).
设计意图在知识的讲解中仍然穿插数学史的内容,同时在每个知识点后安排习题,及时巩固内容.
2.4 课堂小结,延伸课堂
师: 以上就是我们今天学习的新内容,接下来请同学们跟随老师的思路一起回顾今天的学习内容.今天我们通过数字发展的片段了解了数系的扩充过程,并且跟随着数学史的发展站在数学家的角度通过解决一系列问题引入了虚数单位i,并构造新数a+bi(a,b ∈R);为了得到完整的数系定义,我们对复数、复数集及复数的代数形式给出了数学解释;同时我们类比实数得到了复数的分类、复数相等的概念.同学们在学习的过程中有没有体会到用了什么数学思想呢?
生: 类比推理.
师: 很好.复数在实际生活中应用非常广泛,可以用在量子力学、流体力学信号分析等领域.
生: 老师,数系还能再扩充吗?
师: 同学们能提出这个问题说明确实认真思考过了,其实现在也有数学家在研究这个问题,希望同学们经过本节课的学习,能够根据数系扩充的特点寻找数学中的矛盾,说不定有一天你们也能建立一个新的数系.
2.5 作业布置
必修二第70 页练习1、2、3 和研究性作业: 借助信息网络,探究复数在生产生活中的应用,并写一份研究小报告.
3 教学反思
3.1 追随数学步伐,沐浴课堂思政
在数系的扩充和复数的概念这一节的教学中,是在数学史的基础上实施数学教学活动,也就是在具体的数学教学中,根据数学史的发展历程进行设计,从而让学生站在数学家的角度,引导学生重复数系扩充的关键步骤,进一步加深学生对数学思想的理解.数学史作为课程思政的一种形式有助于学生理解数学的发展,将数学知识和数学思想结合起来,使学生更好的把握数学发展的脉络,理解数学的本质,开阔学生的数学眼界,增强其创造性和创新性,知道一些数学知识从何而来,为何而来,是谁历经了困难将其证明出来提供给世人学习,在经历数学史的过程中进行知识的建构,使抽象的数学知识和方法变得更加灵活生动[5].在本节课中,教师将复数的发展脉络呈现给学生,让学生亲身体验虚数单位等的由来、复数体系的建构;同时,也能让学生了解数学家的故事,从而给学生树立正面榜样,激励学生直面挫折,例如数学家卡尔达诺发现了负数平方根但没有承认,从而错失了机会,邦贝利勇于探索负数平方根,进而解决了负数平方根与实数之间的矛盾,启发学生在数学的学习中要有创新思维,勇于突破原有数学知识的禁锢.
3.2 追随数学步伐,激发学生内驱力
课堂如果枯燥无味,学生必然对所学知识毫无兴趣,因此,数学课堂不能只是数学知识的讲解以及练习的循环往复,而是应该让学生真正对数学产生兴趣.因此可以在教学中融入数学史,首先数学史本身就是人类探索的过程,在老师的启发指导下,这些过程很容易被学生接受;其次根据历史发展脉络讲解知识可以加深学生对知识的的体验性,提高学生对数学知识的亲近感;最后,数学家的事迹有助于培养学生学习数学的态度,激发学生的动机[6].将数学史穿插在课堂中,能够激发学生的好奇心和求知欲,激发学生内驱力,从而提高课堂教学效率,增强课堂氛围.

