一种适用于卷积结构的非图像数据预处理方法

黄 涛, 陈颖悦, 陈玉明, 曾念峰

(1.厦门理工学院 计算机与信息工程学院,福建 厦门 361024; 2.易成功(厦门)信息科技有限公司,福建 厦门 361024)

0 引 言

近年来,以深度神经网络(deep neural networks,DNN)为代表的机器学习方法逐渐兴起[1],在其内部可以自动实现对数据的特征学习,提高工作效率.卷积神经网络模型(convolutional neural networks,CNN)作为DNN的代表性架构,更是在机器视觉[2]和图像处理[3]等领域大放异彩.然而,实际生活场景中的基因组[4]、转录组[5]、和金融分析等数据都是非图像形式的;传统机器学习技术(Machine Learning,ML)可以在这些领域取得广泛应用,CNN却因其输入受限而无法适用.幸运的是,国内外的科研人员们从未停止过对这一研究邻域的尝试.Schmidhuber 于1997年研究出了LSTM网络[6],它较好的克服了RNN不擅长处理长序列的问题,在自然语言处理[7]领域得到广泛应用;Yoshua等提出擅长处理序列信号的循环神经网络(recurent neural network,RNN)[8];2017年,Google推出了基于纯注意力机制[9]实现的Transformer网络模型[10].随后,一系列诸如GPT[11],BERT[12]等用于机器翻译的注意力机制的网络模型层出不穷.除了提出新型算法,能否通过其他手段使得卷积结构也能具有处理部分非图像数据的能力.带着这样的问题,从另一个角度出发,从非图像数据的源数据入手,试图改变源数据的格式使其满足卷积结构的输入要求.鉴于此,本文中,笔者在实验中将选自UCI和Kaggle平台的连续型数据分别处理为一维和二维卷积网络能够识别的特征向量以及图像矩阵,结合自定义的卷积网络结构,寻求更加简洁高效的非图像数据处理方法.经过与ML中经典模型的比较,证明了所提出的适用于卷积结构的非图像数据预处理方法能够有效的解决部分非图像数据无法使用卷积网络结构的困境,并能够在分类性能上取得一定的突破.

1 非图像数据的归一化

归一化处理在模式识别[13]中应用广泛,其用途主要分为2类:一类作为特征提取前的预处理技术;另一类是对特征提取后的特征向量进行特征转换.当其作为预处理技术时,可以消除不同特征间的量纲差异,从而获得更好的分类效果.不同的归一化方法适用于不同的数据分布模型.针对一维卷积的数据预处理方法中,选择表现效果较优的标准归一化.

1) 标准归一化(Z-score normalization)

(1)

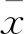
鉴于图像中相邻元素共享相似信息的特点,在处理面向二维卷积结构的数据时采用了对数归一化方法,该方法能够在一定程度上保持原始特征间的关系.

2) 对数归一化(Log normalization)

XMinf=minXtrain(f,:)

(2)

Xtrain(f,:)←log(Xtrain(f,:)+|XMinf|+1)

(3)

XMaxf=max(Xtrain)

(4)

(5)

其中,Minf取自所有训练样本中的最小值,以便使用训练极值对测试集进行归一化操作.如果按最小值调整后,测试集中有特征小于0会被钳制为0;相应的,测试集中大于1的特征钳制为1.此时的数据同样分布在[0,1]之间.

2 非图像数据降维与可视化

为满足卷积网络结构低维和图像数据局部相关的需求,使用经典的T-SNE非线性降维算法对源数据进行特征提取以及可视化操作.

2.1 T-SNE 算法

T-SNE主要用于将高维数据降低维度到二维或三维进行可视化展示[14].实验中将数据降到二维以方便在平面中展示数据信息.T-SNE算法的实现分为2个主要步骤:第一步在高维空间中将样本间欧式距离转换为样本的概率分布,以表达点与点之间的相似度;第二步在二维平面中重构这些点的概率分布,使用梯度下降法优化2个分布之间的KL散度.条件概率pj‖i(x)是样本xi选择xj作为邻居的主要依据.

(6)

其中x∈Rd,σi是以样本xi为中心的高斯方差.与其类似,定义出低维映射样本yi和yj之间的条件概率qj|i.

(7)

DKL(p‖q)=E[lbp(x)-lbq(x)],

(8)

(9)

2.2 非图像数据的可视化

图像由若干个相关像素组成,像素的位置会对CNN的特征提取精度产生一定的影响.实验中通过余弦距离衡量样本之间的相似度并按照相似度大小排列,将相似样本以样本簇的形式插入到图像中,便于有效特征的提取.

将包含d个的特征向量(样本)x通过转置变换可以转换为特征矩阵,利用T-SNE的可视化方法,可以将经过处理的向量放置到二维笛卡尔坐标系中.结合样本之间的相似度,遵循“相似近邻,迥异疏远”的原则确定特征矩阵的位置.此后,每个特征向量都可以在坐标系中确定自己的位置.坐标以(xj,yj)的形式存在,xj,yj分别代表原始特征向量和其在二维平面上的相似映射.确定位置之后将特征值映射到坐标系中,形成每个样本对应的灰度特征图.

图1是使用UCI中的Cargo数据集(它有3 942个样本和97维特征)进行处理后生成的图片样例.

图1 分类标签为1,2,3的样本Fig.1 Sample Images with Classification Labels 1,2 and 3

通过以上图像可以发现,特征值会对灰度图的颜色产生一定影响,这也是卷积神经网络判别不同类别样本的主要依据.

3 自定义卷积神经网络模型

随着深度学习的兴盛,卷积神经网络在计算机视觉和图像处理中的表现大大超越了其他算法模型,呈现统治之势.组合经典的卷积结构组件搭建自定义神经网络模型,用于分析经过预处理的非图像数据,探索卷积结构对连续型数据的适用性.以下详细介绍自定义一维和二维卷积神经网络的构建过程.

3.1 自定义一维卷积网络模型

传统一维CNN多用于处理时序数据,它的输入是一个特征向量和一个卷积核,输出也是一个特征向量.实验中的自定义一维卷积网络模型基于Sequential容器构建,其内部添加由Conv1D层 、BatchNormalization层以及DropOut层组合形成的一维卷积块.卷积得到的相关特征展平后被接着放入全连接层,在输出层中调用Softmax函数进行概率判定,最终得到理想的函数模型.搭建简捷高效的网络模型一直是科研工作者的追求,为了降低网络规模加快模型的收敛速率,采用了1*1卷积核和表现效果较优的LeakyReLu激活函数.紧接着,在模型装配阶段设置了Adam优化器并指定适用于多分类任务的交叉熵损失函数进行参数优化.最后,对封装好的模型进行训练,在其内部启用EarlyStopping机制以保证获得最佳的模型参数,避免过拟合现象的发生.自定义一维卷积网络模型如图2所示.

3.2 自定义二维卷积网络模型

二维卷积神经网络是整个卷积神经网络体系的典型代表,它是图像处理任务的不二选择.自定义二维卷积网络模型由经典的”Conv-BN-ReLu-Pooling”标配单元块以及2个全连接层堆叠而成.不同于自定义一维卷积网络模型,二维卷积模型的卷积层内部分别使用了3*3和5*5卷积核,以便于提取更多有益信息.此外,为了缩减特征图的尺寸,降低网络的参数量,模型中加入了可用于信息聚合的最大池化层.具体的自定义二维卷积网络模型如图3所示.

图2 自定义一维卷积网络模型架构 图3 自定义二维卷积网络模型架构Fig.2 Custom 1D Convolutional Network Model Fig.3 NCNN Network Architecture Diagram

3.3 适用于卷积网络的数据预处理方法

3.3.1 一维卷积网络数据预处理方法(One-dimensional convolutional network data preprocessing method,CNPM1D)

输入:多维连续数据值.

输出:不同类别的概率值.

步骤:

1) 读取数据集,进行数据清洗(填充空白值,删除奇异数据等);

2) 切分数据集指定标签特征,将数据集按照8∶2的比例分割为训练集和测试集;

3) 使用Z-score normalization对数据进行归一化处理;

4) 改变训练集和测试集数据的形状(改为特征向量形式)用于网络的输入;

5) 构建自定义一维卷积模型,指定超参数和早停机制并装配模型;

6) 模型训练、参数保存,可视化训练过程.

3.3.2 二维卷积网络数据预处理方法(Two-dimensional convolutional network data preprocessing method,CNPM2D)

输入:多维连续数据值.

输出:不同类别的概率值.

步骤:

1) 读取数据集、进行数据清洗,指定标签项;

2) 数据随机重采样,降低不平衡数据集对分类结果的影响;

3) 按照8∶2的比例切分数据集;

4) 对数据进行Z-score Normalization归一化处理;

5) 运用T-SNE算法对源数据进行降维操作,使用转置变换将降维后的数据转换为图像矩阵;

6) 可视化得到的灰度图像,判别图像所属类别;

7) 构建自定义二维卷积网络模型,将固定大小为120*120的图像送入卷积模型进行卷积操作;

8) 最后保存模型,使用模型对测试集进行类别判断,进行训练过程的可视化展示.

4 实验分析

为了验证自定义网络模型的泛化能力,在选取数据集时从样本容量、特征数量等多方面进行考量,最终从UCI和Kaggle平台上选取了6个常用的数据集,各个数据集的具体信息如表 1 所示.

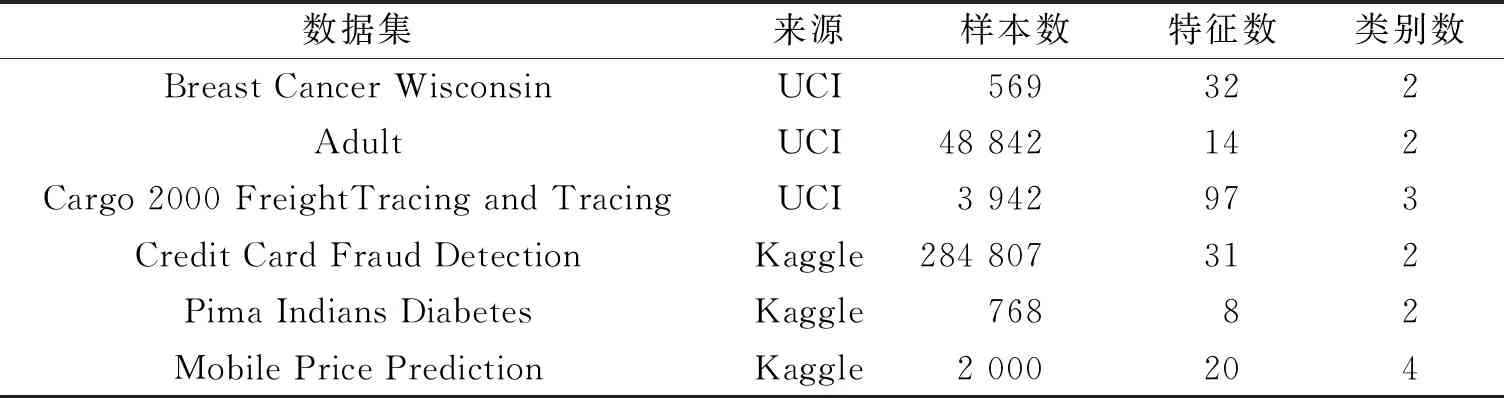
表1 实验中所选用数据集的详细信息Tab.1 Specific Information of the Data Set Selected for the Experiment

提出了2种针对卷积结构的数据预处理方法,分别适用于一维和二维卷积神经网络.实验中以分类精度为评估指标,从多个角度进行数据分析和实验对比,以探究所提方法的实验效果.

4.1 2种自定义模型对比

基于常用卷积结构构建的两种自定义网络模型用于处理经过预处理的目标数据.同一数据集先后被转换为特征向量和图像矩阵,用于比较一维和二维卷积网络模型的分类性能.表2是二者的实验效果对比.

表2 CNPM1D 与 CNPM2D 模型的分类性能对比Tab.2 Comparison of the Classification Performance of CNPM1D and CNPM2D Models

通过数据比较可以发现,相同条件下,一维卷积模型的分类精度要略优于二维卷积,这与2者的适用范围所关联.一维卷积常用于处理信号和时序等连续型数据,二维卷积网络普遍用于图像数据.实验中通过降维,数值转换等手段将原本连续的数值型数据转换为图像矩阵,虽说基本符合二维卷积的实验要求,但必定会在转换的过程中造成有益特征的丢失,产生实验误差.此外,一维卷积结构在处理连续型数据具有先天的优势,产生这样的实验效果也符合设计初期的猜想.

4.2 不同分类方法对比

传统机器学习领域的分类器凭借其简单易实现的特点得到工业界的广泛应用,实验中使用几种经典的分类器模型与所提出的自定义卷积模型进行分类效果比较.其中LR,SVM,DT,GB分别代表逻辑回归、支持向量机、随机森林以及高斯贝叶斯分类模型.表3选用CNPM1D与其他算法进行比较,具体情况如下.

表3 CNPM1D与不同机器学习分类器的性能对比Tab.3 Performance Comparison of CNPM1D with Different Machine Learning Classifiers

不难发现,与其他算法相比,CNPM1D方法在多数数据集上取得了较好的分类效果.在常用的breast cancer wisconsin中,CNPM1D的分类精度高出分类效果最好的LR算法近2.6 %,达到了99.12 %.在多分类问题上,该方法也可以取得较为优异的成绩.例如cargo 2000 freight tracing and tracing上其能够与DT算法一样,取得1.0的精度.虽然它并非在所有的数据集上都能获得最好的分类效果,但相对于其他机器学习算法来说有了一定程度的提升.

4.3 实验效果可视化展示

实验过程中使用可视化技术展现训练过程可以及时发现模型存在的问题,进而调整出更加精确的模型.CNPM1D方法在Breast Cancer Wisconsin数据集上的训练精确度和训练损失如图4-5所示,其中纵坐标的t,v分别代表模型的训练集和验证集的精度,横坐标e代表训练次数,纵坐标a表示精度,l是损失度.

图4 模型训练精确度图 图5 模型训练精确度图Fig.4 Model Training Accuracy Diagram Fig.5 Model Training Accuracy Diagram

通过图4和图5可知,自定义卷积网络模型收敛速度较快,训练过程比较稳定.训练集在数据迭代80～100次之间达到精度顶峰,验证集精确度有所波动但整体上与训练集保持相同趋势.模型的损失呈明显下降趋势,迭代的前20次损失下降最为明显,80～100次迭代期间损失较为平稳,基本达到了最低值;所以该模型在迭代80～100次的情况下可以取得最好的分类结果.

5 总 结

传统的一维CNN多用于时序预测、文本处理等领域,二维CNN在图像处理方面独占鳌头.本文中,笔者从细微处入手,探索卷积网络处理非图像数据(连续数值)的能力.经过实验验证,发现卷积结构在非图像数据上也能够取得优于传统机器学习算法的效果,进而提出了一维卷积网络数据预处理方法(CNPM1D)和二维卷积网络数据预处理方法(CNPM2D).经过与传统的分类模型进行效果对比,发现使用了预处理方法后的卷积模型尤其是自定义一维卷积网络在低维的数据集上效果较好.与CNPM2D结合使用的二维自定义卷积网络的效果虽不一维卷积那么明显,但是也在传统模型的效果上有了一定的提升.此外,不同的归一化方法对实验结果也会产生较大的影响,这就需要在数据预处理之前对数据分布有一个大致的了解,确保可以选择最佳的预处理方法,从而获得更好的分类效果.大数据时代下信息交错、数据互融,需要使用合适的降维算法去除干扰特征,降低网络的复杂度和参数规模;以简单的网络模型完成复杂的任务.此次的实验只是通过简单的方法尝试了卷积网络处理非图像数据的可能性,工作上还存在着很多可研究空间.如何将非图像数据转化为彩色图像,卷积网络结构能否直接处理声音等非连续数值型数据等等.未来的工作中,将继续致力于探索CNN对非图像数据的适用性,完善非图像卷积神经网络的用途.