基于改进蚁群算法的物流无人机路径规划
宁雨舟 赵蕊
(安徽财经大学 安徽省蚌埠市 233000)
快递行业如今存在的问题以及无人机的优势:
(1)快递人员送货车辆不统一,类型较为复杂。在城区中人员来往密集,街上车流量较大,传统车辆送货方式不仅效率低下,而且容易发生交通事故。而无人机相较于这种传统的运送方式,不仅运输效率高,而且其可以不受地面交通情况的影响,安全系数也大大提高。
(2)安全问题和技术问题。电子商务的迅速发展,快递运输过程中的安全问题也越来越被人们所重视;但大部分情况下快递人员都是直接上岗工作的,专业技能有限。而无人机对于人力的要求低,对技术要求同样不高,一个快递员可以同时操作数十架无人机进行送货,大大降低了运送成本,同时使货物在运送过程中的安全性得到提高。
(3)乡村地区派件难,运输成本高。在经济发达的城区快递配送仍存在问题的今天,经济落后的乡村地区快递配送更是难上加难,虽然乡村人流量较小,但是乡村客户分散,物流集中点少,且各配送点之间距离较远,采用车辆运输不仅会出现绕路,还使得配送成本大幅度提高。而无人机的主要能源为电能,可以节省成本,同时,无人机可以去到汽车难以去往的地方,在偏远山区及农村的快递配送过程中将会发挥更大优势。
创新部分:
1 无人机的路线规划
1.1 模型构建
问题描述:假设在某个城市区域内进行无人机配送任务,其中物流仓库与若干起降点的坐标均已知,现在需要寻找一条在无人机从物流仓库出发到达各起降点卸载货物,并返回物流仓库的一条最短最优路线。如何在保证飞机安全飞行,供电充足的情况下寻找到一条最优最短路径将是本实验的重点。蚁群算法是受到20所示50年代仿生学的启发,由意大利学者M.Dorigo 等首先提出的一种新型的模拟进化算法,该算法在求解组合问题中表现出优良的特性。因此,蚁群算法也一直被用来解决路径规划问题。蚁群算法求解路径问题的关键部分是在信息素矩阵的更新。更新的结果直接导致蚁群算法的最优路线。每一代蚂蚁行走的路线表示待优化的可行解,蚁群行走的所有路径构成解空间,每一只蚂蚁行走的时候都会释放一种信息素。随着时间的推进,每一代蚂蚁走过的相同路径的信息素就会越来越高(当然也会伴有一定数量的信息素挥发),那么信息素较高的路径就有更大概率被选择,从而找出更优路线。
1.2 环境模型构建
若要对无人机的配送路径进行科学的规划,首先要对城市的三维飞行环境进行建模。本实验采用栅格法对城市模型进行建模,栅格法是利用VB 等软件对地图建模的一种方法,简单来说就是将障碍物模拟成小方格的集合,相当于将场景的所有事物进行二值化替代,障碍物为1,非障碍物为0。假设该城市区域是一个三维空间中的长方体,其长宽高分别由a,b,c 个正方体栅格所组成。其中a=ROUNDUP(xmax/Mlength),b=ROUNDUP(ymax/Mlength),c=ROUNDUP(zmax/Mlength),Mlength为每个栅格正方体的长度,xmax,ymax,zmax,为三维长方体模型的长宽高,ROUNDUP()为向上取整函数。栅格法构建完成后飞行的环境如图1所示,当无人机从物流仓库出发后,经历各起降点选择一条最优最短的路径飞行。
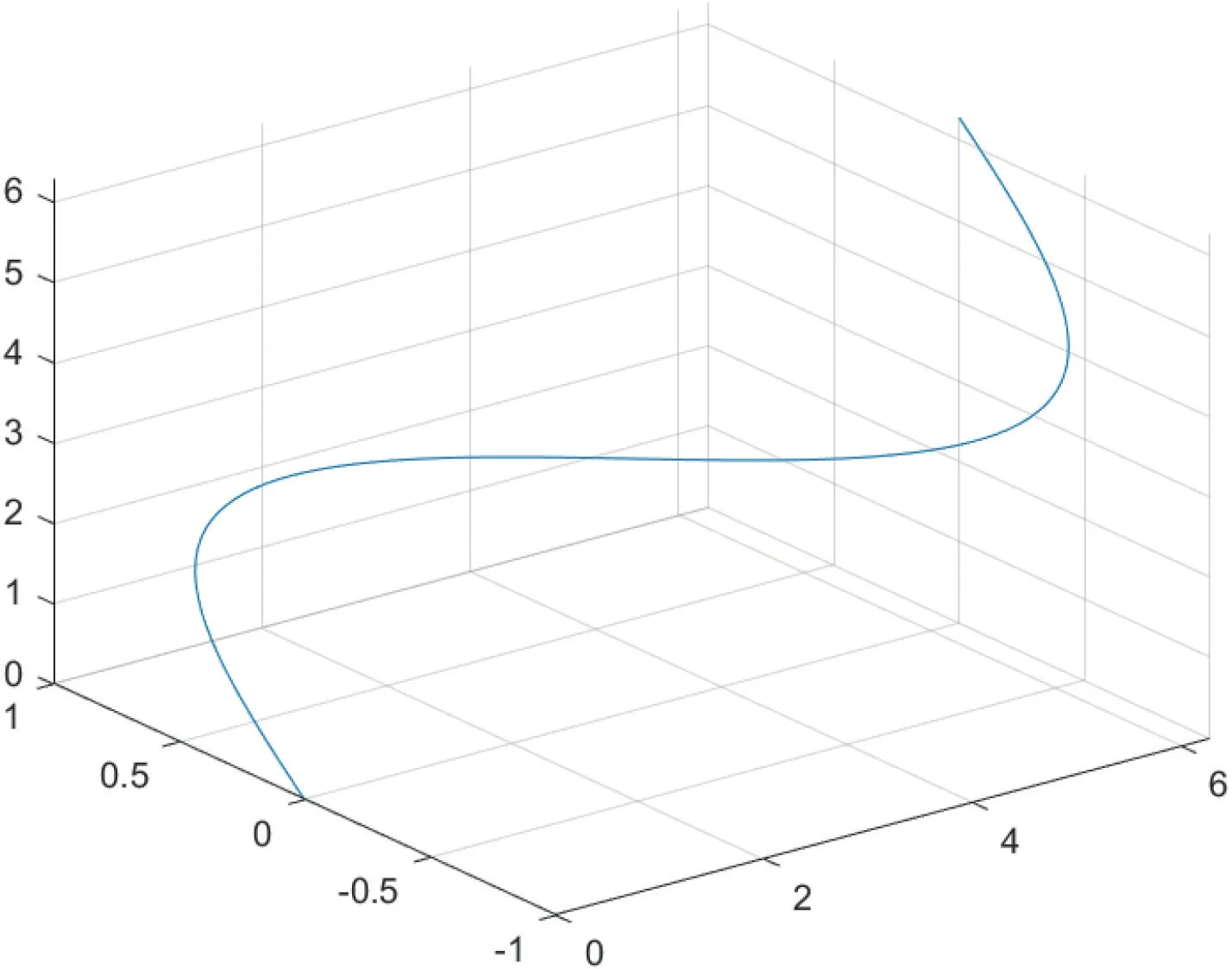
图1
1.3 约束条件
(1)最大载重约束:由于无人机大小以及动力限制,无人机可运送的货物重量也必须控制在一定的范围内,否则会增加飞行过程中的安全隐患,同时难以完成正常的配送任务。
(2)最大续航约束:无人机电池的存储能力有限,考虑到无人机的起降以及在特殊情况下的悬停造成的耗能,无人机的整个配送过程中的耗能应为其电池最大储能的85%~90%。
(3)最大高度约束:通过栅格法对环境模型的构建,无人机在配送过程中高度的确定除了不能超过该城市约定的最大高度外,还应考虑到配送路径上各建筑的高度。
(4)最大转弯角度约束:为保证无人机在运输过程中飞行姿态的稳定以及对货物的保护,其在配送过程中的转弯角度应当小于其最大转弯角度。
2 模型求解
2.1 蚁群算法
2.1.1 传统的信息素浓度
在真实环境里,随着时间的推移蚂蚁释放的信息素会逐渐蒸发。假设蒸发速度一定,那么在相同时间内,信息素浓度越高的路径残留的信息量则越多。这一特性对下一代蚂蚁寻路有很好的指导作用。据此,给出信息素的更新公式:
式中,τij(t)为t 时刻在ij 连线上残留的信息量,初始时刻设每条路径上的信息量相等,即τij(t)=C(C 为常数),ρ 为新系数残留系数(取值在0~1 之间), 表示第k 只蚂蚁在本次循环中留在路径ij 上的信息量。
在这些计算公式的假设下,用不同的方式设置这些参数,即有以下三种模型:
(1)Ant-Circle System 模型(也称蚁圈模型)。根据M.Dorigo 的Ant-Circle System 模型,有:
式中Lk为第k 只蚂蚁在本次循环中所走路径长度,Q 为常量。
(2)Ant-Quantity System 模型(也称蚁量模型)。
式中dij为节点i 到节点j 之间的距离。
(3)Ant-Density System 模型(也称蚁密模型)。
在以上三种模型中,后两种模型都是利用的局部信息,而第一种模型利用的是整体信息。
2.1.2 选择概率
ηij=1 ⁄dij
2.2 A*算法
A*被广泛应用于路径规划的启发式算法,通过估价函数f*判断无人机的飞行轨迹点的优劣,引导算法快速收敛,即:
f(x)=g(x)+h(x)
g(x)为起点到当前节点的实际代价,h(x)为当前节点到终点的预估代价,即启发函数。
用A*算法进行路径搜索时,可将搜寻区域简化成一组可量化的节点,查找最短路径时,从起点开始,检查其相邻的方格,然后向四周扩展,直至找到目标。
3 基于A*算法的蚁群算法改进
3.1 残留信息量改进
设m 为蚁群中蚂蚁的数量,n 为包含配送中心在内的所有配送点的数量,dij(i,j=1,2,3,4,...,n)为配送点i 到配送点j 的距离,bi(t)为t 时刻位于配送点i 的蚂蚁只数。如果在时间间隔(t,t+1)中,m 只蚂蚁都从当前城市选择下一个城市,则经过n 个时间间隔,所有的蚂蚁都走完n 个城市,构成一轮循环,此时按照以下方法修改各条路径上的残留信息:
式中,L.set为所有蚂蚁经过路径ij 点在本次循环中所走路径长度L 的集合。
3.2 选择概率改进
f(xj)为估价函数,通常估价函数越小越容易被选择,所以这里使用估价函数的倒数。
3.3 估价函数——f(xj)
f(xj)=g(xj)+h(xj),通常情况下取启发式函数h(xj)=djs(djs为当前位置到终点的距离),但由于该路径起点和终点是同一个位置,不能用欧氏距离求解当前位置到终点的距离。同时,配送问题仅仅只考虑距离问题远远不够,因此,设置代价函数时考虑以下两点:
(1)距离某两个配送点距离相同,优先考虑配送较重的物件。
(2)全局配送距离的能耗。
然后以一定的权重将这两点加入到代价函数中。
如图2所示,如果L1=L4,在配送点1 可卸货物重量m1 大于在配送点m3 可卸货物重量,那么按照图中配送方式相比于从“起点→配送点3 →配送点2 →配送点1 →终点”将会更加节能。
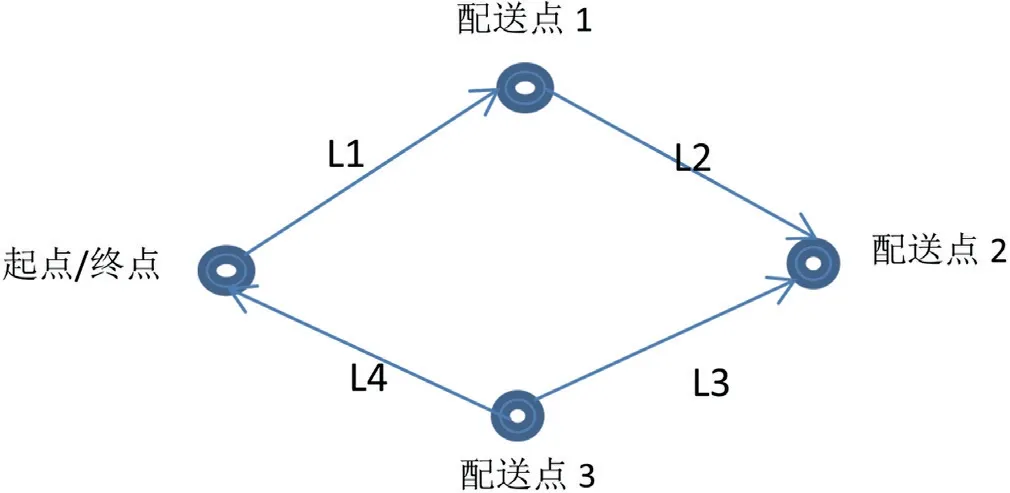
图2
据此设置代价函数f(xj)如下:
f(xj)=μ*g(xj)+λ*h(xj)
μ、λ 是对代价函数g(xj)和启发式函数h(xj)设置的权重。满足:μ+λ=1 且λ>0.5。
3.4 代价函数——g(x)
mi表示无人机在配送点i 的重量,(xi,yi)表示无人机在配送点i 的坐标,(xj,yj)表示无人机在配送点j 的坐标。配送点i 和配送点j 是配送路径中两个相连续的配送点。当i=0 时,则认为是起点。
3.5 启发式函数——h(xj)
h(xj)=mj*(Lk-d0j)
Lk表示蚂蚁在本次循环中所走过的路劲长度,d0j表示起始点到配送点j 的距离。
如图3所示,如果L1=L4,在配送点1 可卸货物重量m1 大于在配送点m3 可卸货物重量,那么按照图中配送方式相比于从“起点→配送点3 →配送点2 →配送点1 →终点”将会更加节能。
图3
3.6 算法流程
实验仿真:
3.6.1 初始化参数
本次实验在matalb 软件下进行仿真,用m×m 大小的宫格模拟试验环境,黑色方格表示障碍物,白色方格表示可行点,红色方格则表示算法走过的路径。最大迭代次数Nmax为100,每条路径的初始信息量C 为8,初始无人机数量m 为50,L.set,allowed集合初始化为空。
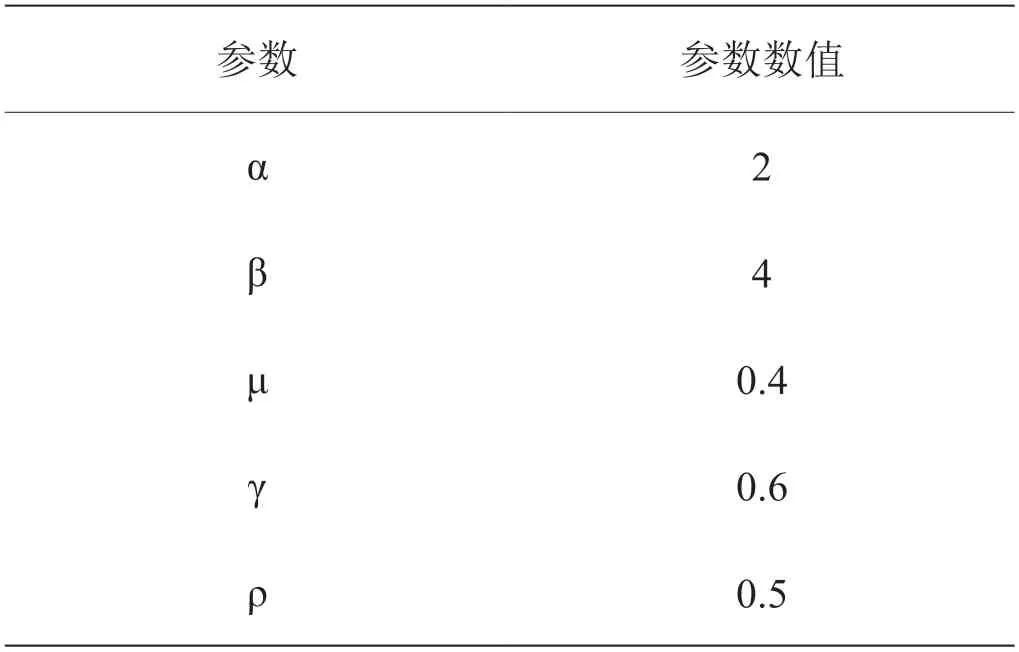
参数参数数值α 2 β 4 μ 0.4 γ 0.6 ρ 0.5
3.6.2 实验仿真数据
(1)未优化仿真路径;
如图4所示。
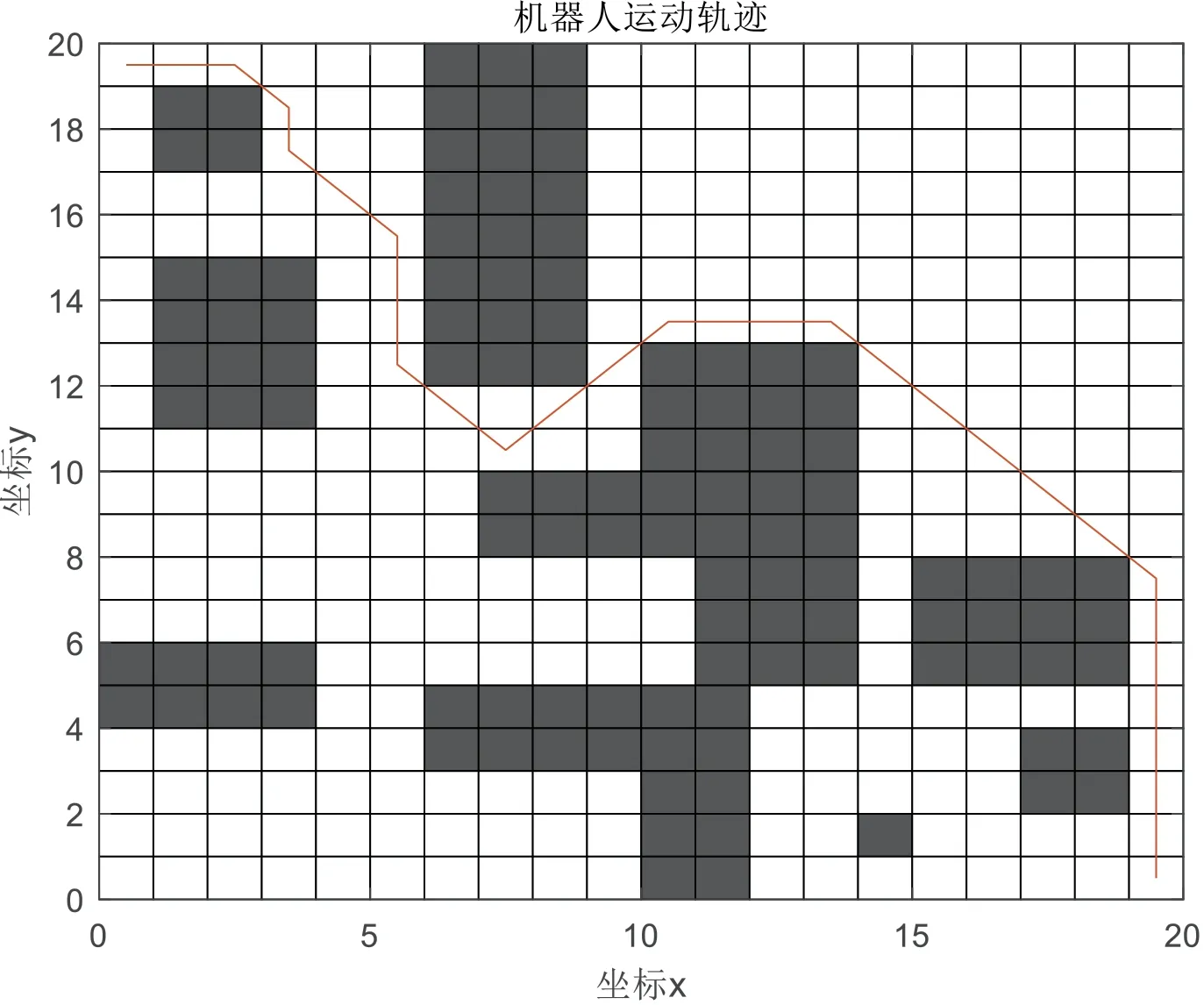
图4
(2)经优化后仿真路径;
如图5所示。
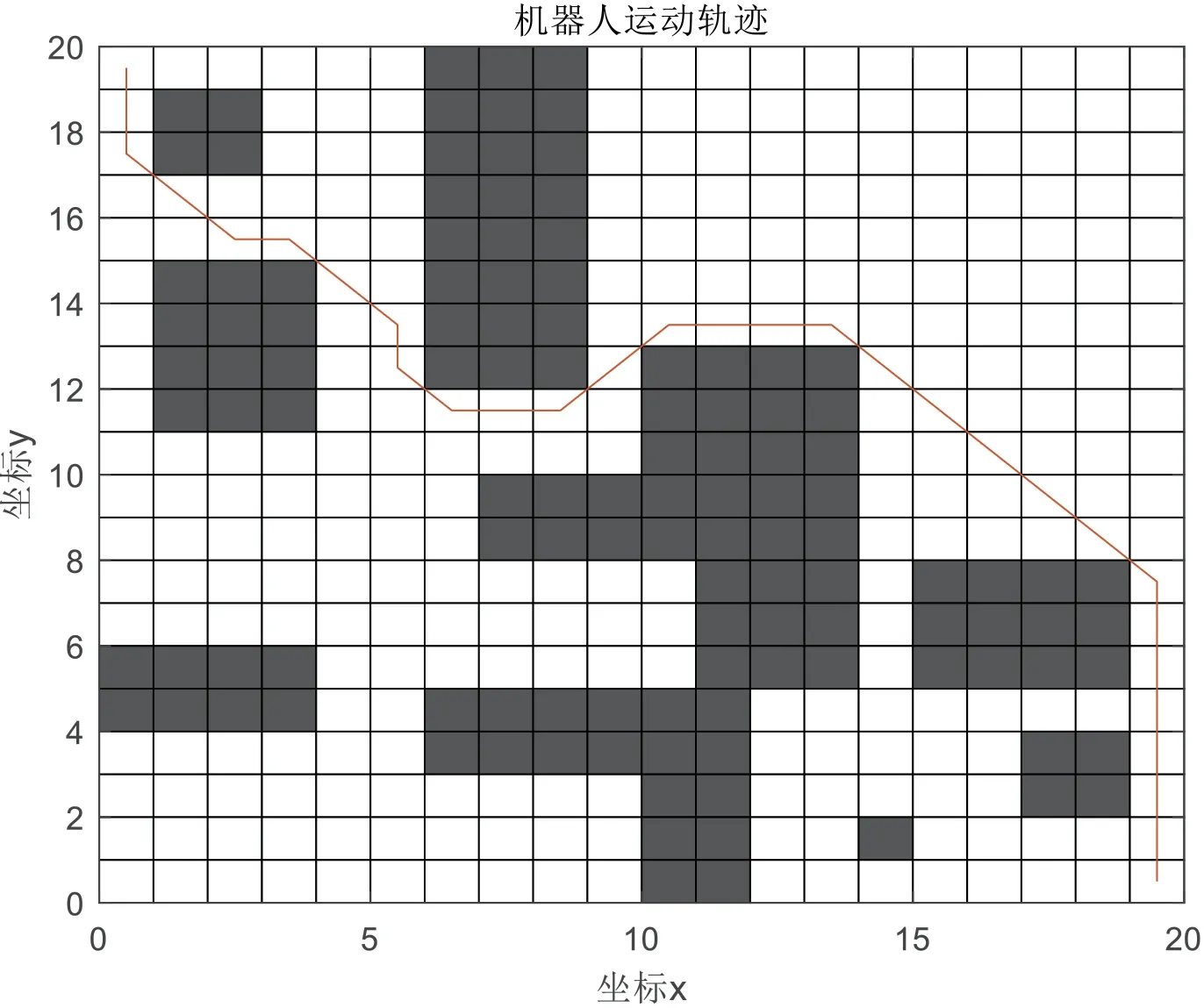
图5
(3)实验分析。
改进的蚁群算法计算出可行节点的选择概率之后,使用轮盘赌对可行解点进行选择,经过一轮循环之后,构建出一组可行解。通过以上实验数据分析得出:改进后的蚁群算法收敛速度更加稳定迅速,寻找最优路径的能力相较于传统的蚁群算法较为显著。
4 结语
本文针对城市环境中无人机的路径规划问题,利用栅格法对城市环境进行三维模型构建,同时考虑到无人机在运输过程最大载重,最大续航,最大高度,最大转弯角度等约束条件,提出了一种基于A*算法的改进蚁群算法。在模型的求解中,通过对残留信息量以及选择概率的改进,引导系统向最优解的方向进化。引入估价函数,代价函数,启发式函数,使无人机在路径规划以及能源消耗方面更具优势。仿真结果表明,改进的蚁群算法在路径点数、时间规划、能源消耗方面都具有明显减少。证明了该改进算法的可应用性。

