基于神经网络的铜矿伽马能谱分析

尤瀚庭 樊港

（东华理工大学机械与电子工程学院 江西省南昌市 330013）

能谱识别技术作为核与辐射探测领域的关键性技术，国内外相关专家一直致力于该技术的理论研究与技术创新。由于探测器性能、背景噪声等因素的影响[1]，传统核素识别在处理复杂能谱数据时，误差较大，识别率较低[2]。为了克服这个难题，近年来针对能谱这种高维度、非线性的数据，全谱分析方法逐渐得到发展，主要工具有人工神经网络、粒子群算法、K-L 变换等[3]。

近年来计算机技术飞速发展，为了使机器设备在处理复杂数据时具有智能思维能力，人工神经网络（ANN）在最近三十年中不断发展。目前，基于神经网络的全谱分析方法受到重视。1991年，Olmos 等人[4]首次提出了在伽马能谱分析中使用人工神经网络。1995年，Keller等人[5]使用人工神经网络进行核素识别，从结果可以看出，人工神经网络提高了核素识别速度与准确度。2015年刘议聪等人[6]提出了基于人工神经网络的核素识别方法，使用主成分分析法（Principal component analysis，PCA）提取主要特征，实现数据降维。2019年Liang 等人应用空间填充曲线将1*1024 的伽马能谱转化为32*32的二维数据，具有更快的收敛速度和更小的损失函数[7]。2020年，王瑶等学者通过滤波平滑等数据处理方法处理放射性核素能谱数据，研究长短期记忆神经网络（Long Short-Term Memory，LSTM）算法[8]在核素识别领域的应用。

由此可见，神经网络解决伽马能谱分析问题已经成为该领域的热点。本文主要使用神经网络处理PGNAA技术探测铜矿后产生的特征伽马能谱。由于实测数据不足，采用MCNP 仿真软件构建数据集，通过设计卷积神经网络模型完成对模拟伽马能谱的分析。

图1：矿石与相关概念的关联[9]

1 数据集构建

神经网络的训练需要大量数据，实验获取的数据数量不足以支撑神经网络的训练，故需要采用模拟的方法构建数据集。本文采用MCNP 软件，基于蒙特卡罗方法生成伽马能谱。MCNP 软件是国际公认的分析中子和伽马射线输运问题的程序，其主要输入文件有栅元卡（定义构成整个系统的各个基本介质单元及相应的物理信息）、曲面卡（定义组成栅元的曲面信息）、数据卡（包含反应类型、源描述、材料描述等其他信息）。使用MCNP 方法构建数据集的难点在于MCNP 是基于统计理论的软件，如果输入文件的数据卡中矿石元素含量不发生变化，则基于伯努利大数定律，最后的结果会非常接近，不利于提升神经网络的鲁棒性。因此使用MCNP构建数据集将矿石样本不足的问题转变为铜矿石元素含量如何构成。

矿石一般由矿石矿物和脉石矿物组成。矿石矿物又称有用矿物，是可以被利用的金属或非金属矿物。脉石是指与有用矿物伴生的无有用组分且没有可用性能的矿物，又称为无用矿物[9]。因此，铜矿其实是有用矿物和脉石的组合。本研究选取江西铜矿相关研究记录的350条金属矿物的电子探针探测结果，300 条各种脉石的化学成分分析结果，通过按照不同比例混合脉石与金属矿物得到了1600 条模拟铜矿数据。

根据我国的采矿技术，铜矿边界品位一般为0.2%，工业品位为0.4-0.5%，0.5-1.4%的为低品位矿石，1.4-2%的为中等品位矿石，2%以上的为高品位矿石[10]。由于数据集类别不均衡，将脉石与低于边界品位的铜矿作为第一类，边界品位到工业品位（0.2-0.5%）矿石合并为第二类，将低品位矿石与中等品位矿石（0.5-2%）合并作为第三类，铜矿品位超过2%的作为第四类，以此为标准设立多分类标签。

此外，铜矿床中常伴生有铅、锌、铁等元素，当伴生元素达到一定含量时不可以忽略其经济价值，需要进行综合评价和回收考虑。伴生矿物随主矿产一同开采加工，不会格外产生采矿、运输、破碎等费用，但伴生矿物需要分离与提取，某些情况下需要特殊的生产装置，故需要在核算经济成本的条件下合理回收。

基于表1，对每个模拟数据中上述元素含量大于综合利用标准的设为正类，反之为负类，构建标签数为5的多标签数据集。

表1：常见伴生矿物工业综合利用标准[10]

2 数据二维化

能谱数据与时间序列存在一定相似性。目前，空间填充曲线法、格拉姆角场和马尔科夫转移场常用于将一维数据转换成二维数据。其中，格拉姆角场的优点是其主对角线包含原始值与时间信息，因此可以通过主对角线重建序列。本文采用此方法进行能谱数据二维转换[11]。

对于一个待转化的铜矿伽马能谱序列Y={y1,y2,…,yN}，N=1,2,…,1024， 首先将能谱序列Y={y1,y2,…,yN} 中的每一个值都进行规范化，规范化后记为中的每一个值 都在[-1,1]的区间内。规范化公式如下所示：

使用反三角函数将每个 变为极坐标系下的角度φi，φi的区间为[0,π]。对应的极坐标半径ri采用其所在道址数ni和道址总数N 的比值表示，因此ri处于(0,1]的区间内。具体公式如下：

利用式（1）和式（2）对能谱序列进行缩放后，将直角坐标系中的能谱序列使用极坐标表示，通过每个点之间的角度和来进行格拉姆求和角场（Gramian Angular Summation Fields，GASF）定义，GASF 如下所示：

通过GASF 矩阵，一维的铜矿伽马能谱转化为二维形式，且包含伽马能谱不同道址的信息之间的联系。但从上式可以得知，GASF 矩阵大小为N×N（本文数据N为1024，即1024×1024）。对于铜矿伽马能谱数据来说，采样道址总数为1024，导致GASF 矩阵维度极大，不利于后续处理[12]。

从图2 中可以看到，能谱数据中前200 道的计数远超其他道，在变为格拉姆求和角场时，其他道址的数值由于经过压缩导致GASF 矩阵中200 至1024 道的信息损失严重。为此，借鉴NLP的分词思想，将能谱进行分割，提出分段式GASF 变换。将1024 道的能谱信号分为16个64 道的信号，并采用k=2 的PAA 算法[11]进行压缩。此外，由于900 道之后探测器的探测效率极低，900 道之后对应的能量段内的特征峰几乎都被统计涨落淹没，因此897道至1024道共128道的数据采用k=4进行压缩。1024 道的能谱数据最终转换为15*32*32 的矩阵，与直接转变相比，该方法可以将GASF 矩阵的数据大小缩小约60 倍且保留大部分信息。能谱经过变换后第449～832道的能谱图像如图3。

图2：对1024 道进行GASF 变换的结果

图3：能谱449 ～832 道变换结果

对比图2 与图3，由于分段GASF 方法以每段中数值最大与最小的点为标准进行缩放，避免了不同谱段数值差距过大导致的GASF 方法变换过程中带来的信息损失。同时，所有数据都被限制到[-1,1]之间，相当于对所有数据进行了一次规范化，保证了所有数据处于同一数量级下，避免数值过大的数据占据过大的权重，有利于神经网络的收敛。

3 神经网络搭建与结果

卷积神经网络（CNN）可以在监督模式下自动学习训练权重，并不断从样本数据中提取特征，其对于图像识别有很好的效果。卷积神经网络的结构特性包括稀疏连接、权值共享、时间或空间上的下采样。卷积神经网络主要由卷积层、子采样层和全连接层组成。卷积运算后，样本特征将映射到下一层，然后使用该层提取数据特征。卷积层和采样层交替形成输入层的特征提取层，然后将特征提取后的数据用作新的输入层，继续提取特征。最后，这些特征信息在经过作为分类器的全连接层计算后，在输出层得到分类结果。

在卷积神经网络中，设I(t)为模型输入，s(t)为卷积映射，K(t)为卷积核，那么卷积运算如下所示：

基于卷积神经网络的铜矿品位分类是多分类问题，有益组分识别是多标签问题。通过one-hot 编码，多分类任务标签可以转换为标签个数为4 的多标签形式。因此两个任务的损失函数均选用二元交叉熵损失函数（Binary Cross Entropy Loss，BCELoss），其定义如下：

其中yi是第i 个样本的真实标签，值为0 或1，pi表示预测第i 个样本为正例的概率。使用BCELoss，要求样本必须属于[0,1]，故本文模型的全连接层全部使用Sigmoid 激活函数。在Pytorch 架构下使用BECWithLogitsLoss，该损失函数在进行损失计算之前自动对全连接层的输出进行Sigmoid 操作。

经过分段格拉姆角场变换后，神经网络的输入从1*1024 转变为15*32*32，通过Pytorch 构建如图4所示的ResNet 神经网络，Resblock1 维持通道数与图片高宽不变，Resblock2 则将通道数翻倍、图片高宽减半，Resblock2 与最大池化层的不同在于最大池化层只会使图片的高宽减半而不增加通道数。由于图片高宽仅有32*32，因此在最大池化层与Resblock2 一共5 次图片高宽减半的作用下，最后可以得到480*1*1 的块，通过两次全连接得到最终的结果。

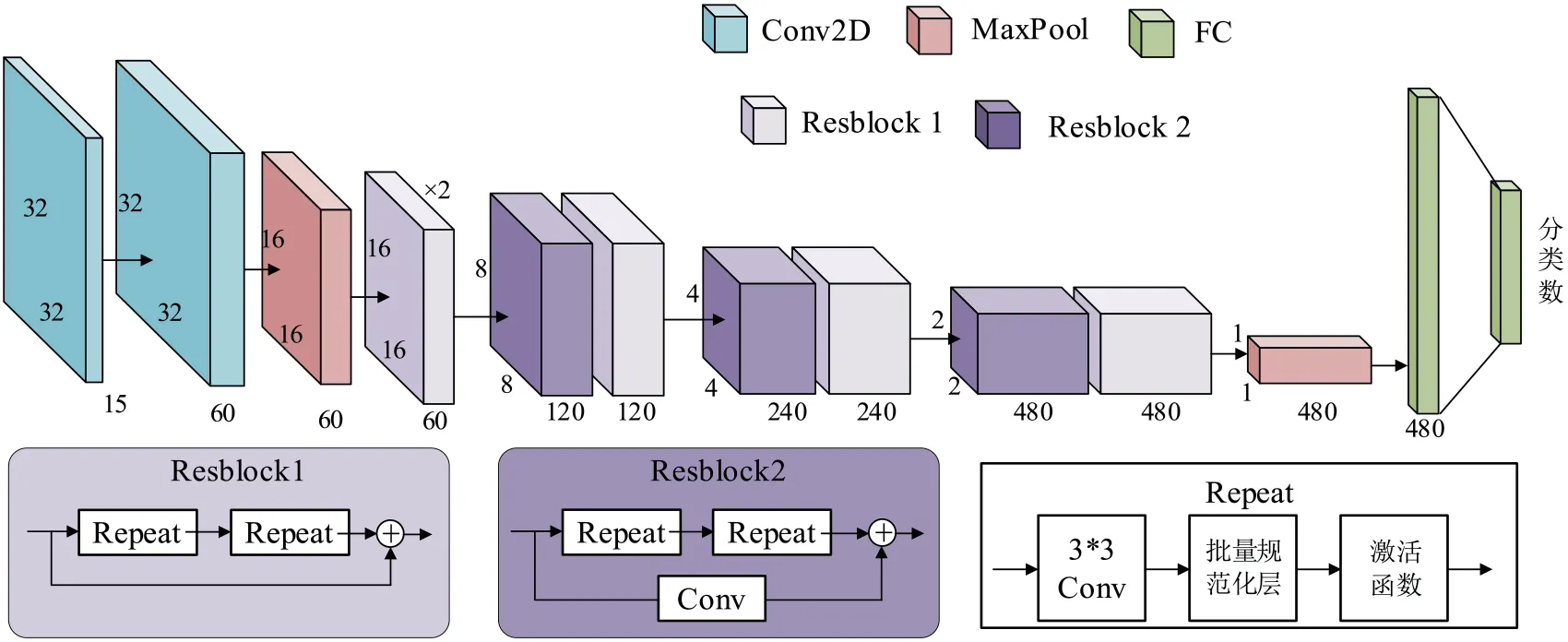
图4：ResNet 网络结构

ResNet 在多分类与多标签任务上的准确率如图5所示，由图中可以看出铜矿中多种有益组分识别任务比铜矿石品位分类任务的准确率低，且模型收敛速度更慢。铜矿品位分类任务在230 多个epoch 左右模型即收敛，准确率在450epoch 时达到94.9%。有益组分识别任务在300epoach 左右仍有较大波动，在训练中还出现了准确率大幅下降的情况，最终识别准确率为93.9%。

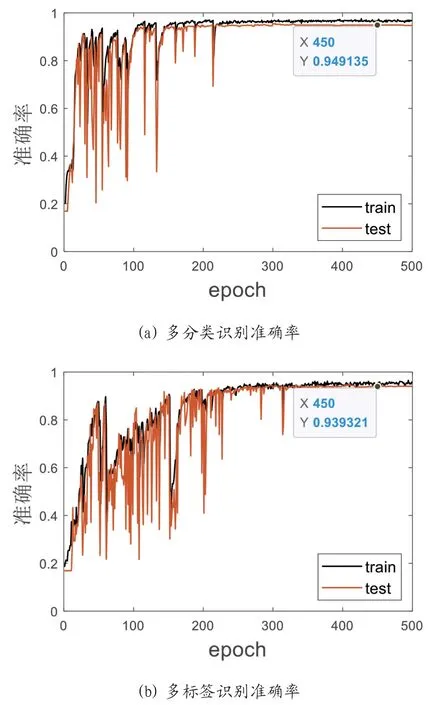
图5：ResNet 对两种任务的准确率

除了ResNet 网络，本文还使用了一些常用的机器学习算法和神经网络模型进行对比，结果如表2。

表 2：各种算法识别准确率

从表2 中可以看出，深度学习对比传统机器学习具有较大的优势，而本文提出的分段格拉姆角场变换联合ResNet 神经网络进行铜矿能谱识别的方法准确率最高。

4 结论

本文通过MCNP 仿真软件构建了1600 条铜矿伽马能谱。由于伽马能谱各道址之间的计数差距极大，提出分段格拉姆角场二维化方法，将一维的能谱数据转变为包含计数与道址信息的二维数据，并联合ResNet 神经网络对伽马能谱进行分析。经过实验，该方法的准确率最高，对于MCNP 模拟铜矿伽马能谱进行的铜矿品位分类与有益组分识别任务准确率分别达到94.9%和93.9%。