Assembly Unit Resource Balancing Strategy based on Discrete Production Mode

REN Qingchuan

(1. Sichuan Jiuzhou Electric Group Co., Ltd., Mianyang 621000, China; 2. Sichuan Avionics-System Laboratory of Lightweight Design and Manufacturing Engineering, Mianyang 621000, China)

Abstract：Aiming at the characteristics of obvious block division and strong discreteness in the assembly production mode of electronic products, this paper proposes a composite U-shaped flexible assembly line model, and establishes a multi-objective optimization mathematical model on this basis. According to the characteristics of the model, the improved ranked positional weight(RPW) method is used to adjust the generation process of the initial solution of the genetic algorithm, so that the genetic algorithm can be applied to the block task model. At the same time, the adaptive cross mutation factor is used on the premise that tasks between different blocks are not crossed during cross mutation, which effectively improves the probability of excellent individuals retaining. After that, the algorithm is used to iterate to obtain the optimal solution task assignment. Finally, the algorithm results are compared with actual production data, which verifies the validity and feasibility of the assembly line model for discrete production mode proposed in this paper.

Keywords： discrete production mode; composite U-type flexible assembly line; genetic algorithm; resource balance

1 Introduction

The assembly production mode of electronic products has the characteristics of obvious block and high discreteness. The construction mode of flexible assembly line often becomes the bottleneck of intelligent manufacturing in military industry. The difference between the assembly process of electronic products and the assembly process of civil products is that the assembly of electronic products usually needs to be checked with the assembly, so that the problems can be returned to the assembly station in time for repair. Therefore, the assembly process is divided by the detection process and has obvious block characteristics. The traditional whole U-shaped assembly line is L-shaped along the assembly time axis in the local range, the reverse is not good, and the detection task can only be located after the same block assembly task, which has a great influence on the assembly line balance.

The composite U-shaped flexible assembly line model needs to optimize the assembly task allocation under the consideration of assembly line balance. The common methods include linear programming[3-6], particle swarm optimization[7-10], bee colony algorithm[11-12], genetic algorithm[13-14], hybrid algorithm[15-16], etc. Genetic algorithm is widely used because of its good convergence and high robustness. References [17-19] used genetic algorithm for mixed assembly line; references [20-21] applied genetic algorithm to assembly line with random operation time; In references[22], genetic algorithm is applied to wire harness assembly line. The above researches show that genetic algorithm is suitable for solving various assembly line problems.

However, the actual test block problem in the assembly of electronic products has not been considered in the process of task allocation and resource balance. The layout and simulation models are unreasonable, and the solutions of various intelligent algorithms are difficult to implement in actual production. Therefore, this paper proposes a composite U-shaped flexible assembly line model. Based on the characteristics of task block, this model adjusts the overall U-shaped structure into a series of small U-shaped structures. The tasks in each block are assigned to a small U-shaped, and the external of several small U-shaped series also constitutes a U-shaped. On this basis, genetic algorithm is used to solve the optimal assembly line balancing task allocation scheme. In this paper, the generation process of the initial solution of the algorithm is improved to adapt to the new model, and the improved RPW method[23]is used to improve the quality of the initial solution. In addition, the adaptive probability is used to keep the excellent individuals as much as possible and improve the mutation probability of the poor individuals. Finally, the algorithm is applied to the actual production line, which effectively improves the production efficiency of the optimized discrete assembly line.

2 Task partitioning and assembly line

The proposed model consists of two parts. The first part is the assembly task block model, and the second part is the composite U-shaped assembly line model. The first part is formed by dividing the assembly task into blocks; the second part is formed by adjusting the assembly line structure.

2.1 Assembly task partitioning model

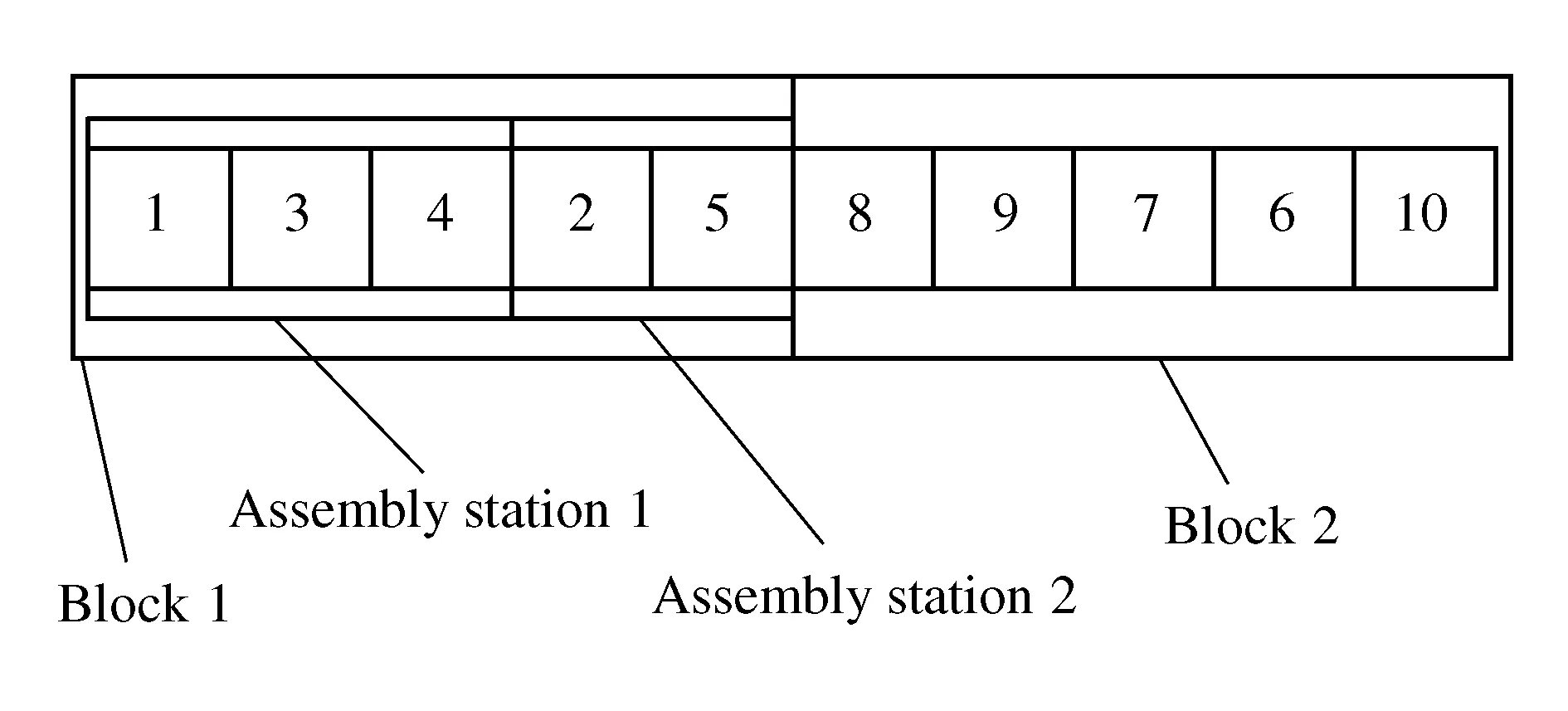
In the assembly production mode of electronic products, the workstation is the basic unit, in which the assembly quality of this part needs to be tested after completing some assembly tasks. Therefore, the detection operation is characterized by obvious assembly process block. Considering this feature, the assembly process is divided into blocks to make the whole assembly process modular. Thus the assembly task block model is established. The block examples in Figure 1 are used to illustrate that 5 and 11 are detection tasks. The dotted line divides all tasks into two parts. The first part is 1-5, and the second part is 6-11.

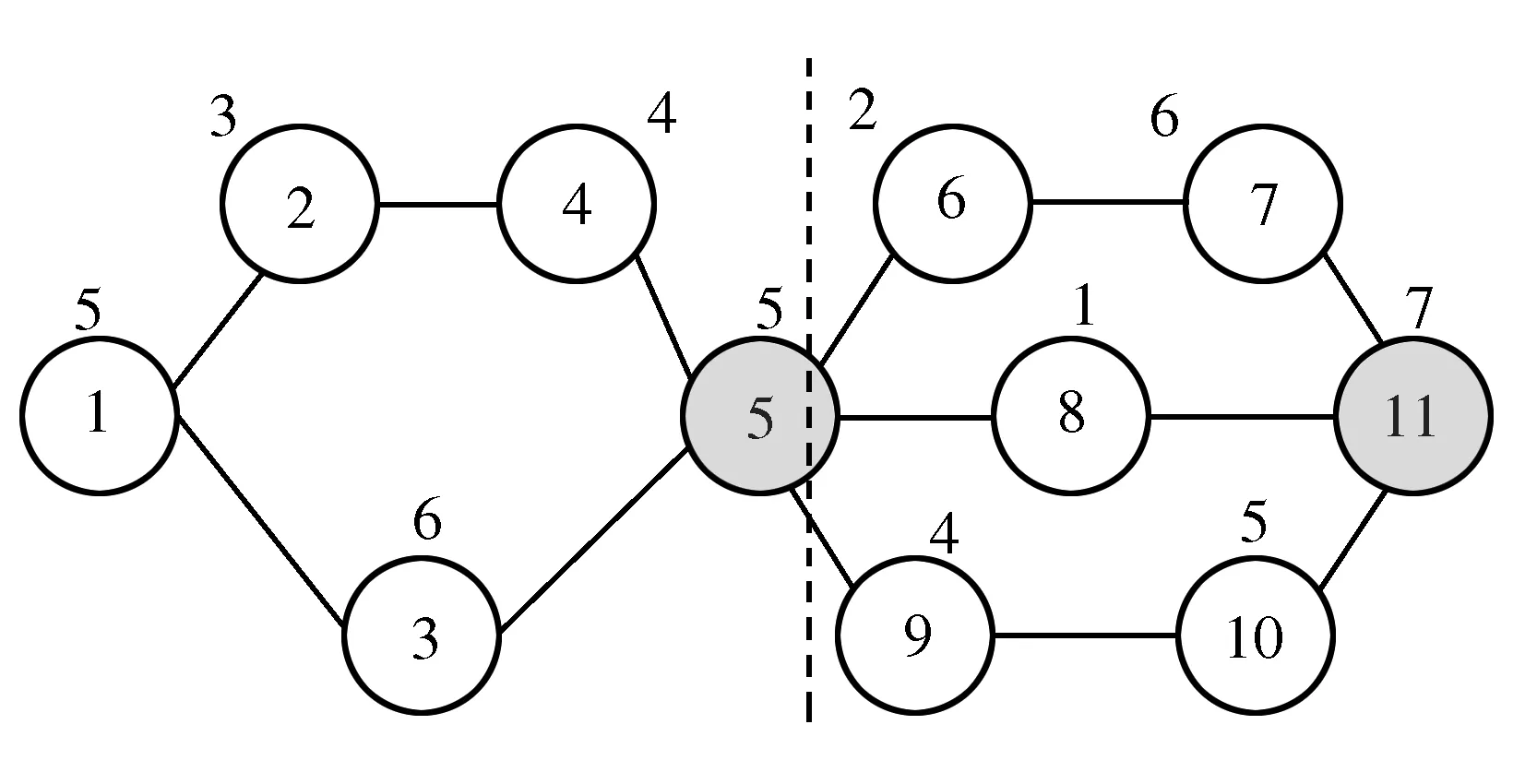
Figure 1 Partitioning example

2.2 Composite U-shaped assembly line model

After establishing the assembly task block model, in order to adapt to the characteristics of its block, the assembly line is adjusted, and the composite U-shaped flexible assembly line model is proposed. This model is based on the traditional whole U-shaped flexible assembly line, which is divided into blocks on the original whole U-shaped structure. Each block forms a small U-shaped structure, and several small U-shaped structures are connected in series to form a large U-shaped structure of the whole assembly line. The composite U-shaped assembly line after block is shown in Figure 2 and Figure 3. Among them,A,B,CandDrepresent the divided blocks,C1,C2andC3are the smallest unit workstations in each part.

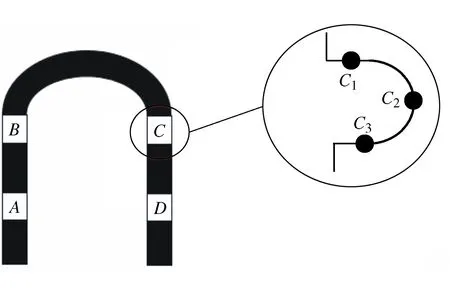
Figure 2 U-shaped assembly line partitioning

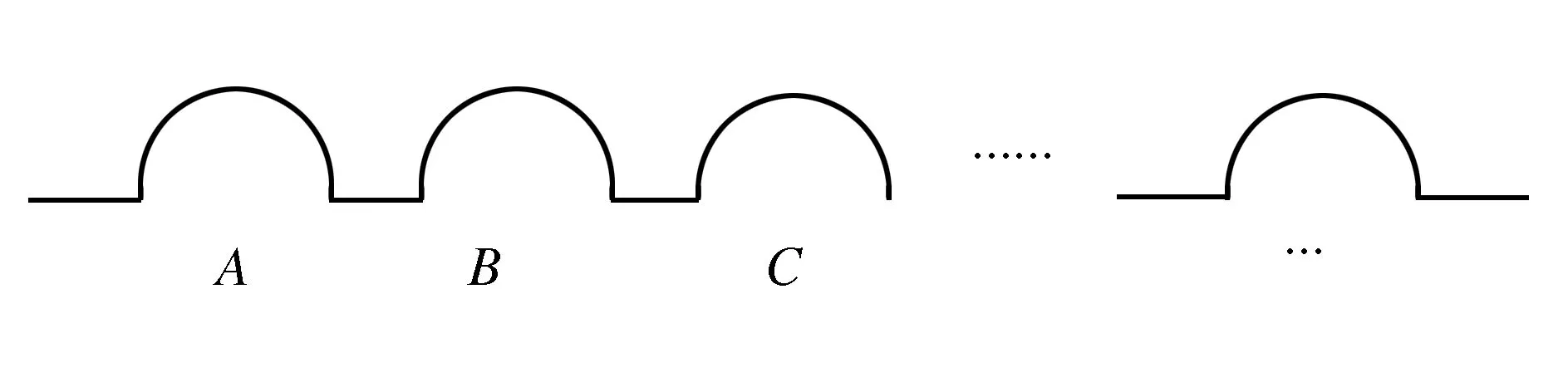
Figure 3 Composite U-shaped assembly line

Considering the external structure, the movable trajectory of the assembly personnel on the line after the block is completed is shown in the dotted line in Figure 4, where the dotted lineArepresents the moving trajectory within the block, and the dotted lineBrepresents the moving trajectory between the blocks. TrajectoryArelies on a small U-shaped structure to achieve resource scheduling in the block. The trajectoryBinherits the characteristics of the traditional U-shaped assembly line and realizes the scheduling of inter-block resources. The existence of these two trajectories improves the flexibility of resource scheduling on the entire assembly line.

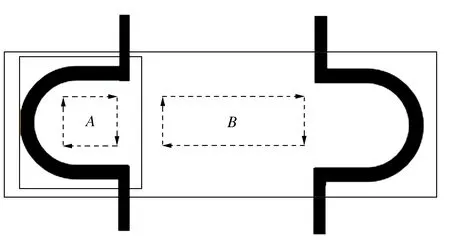
Figure 4 Assembly line moving path

3 Composite U-shaped assembly line balancing model

3.1 Model assumptions

To simplify the mathematical model of composite U-shaped flexible assembly line, the following assumptions are proposed:

1) Only considering the normal assembly time consumption, not considering the workpiece transportation time, waiting time and failure time.

2) After dividing the block, the task of the next block is not associated with the task of the previous block.

3) Each assembly process takes a fixed time, if not fixed, use the expectation of normal distribution of process time.

4) Do not consider the assembly process, assembly quality does not meet the requirements to return to repair.

3.2 Symbol description and mathematical model

1) Symbol description

iis the task number;

Iis the total task set,I={1,2,3,4,…,n}, wherenis the total number of tasks;

Jis the total station set,J={1,2,3,4,…,m}, wheremis the total station number;

Kis the assembly task priority relation matrix;

CTis the equipment beat time;

RTis the set of remaining time,RT={rt1,rt2,rt3,…,rtj}, wherertjdenotes the remaining time of the workstation with station numberj;

Tis the task time set,T={t1,t2,t3,…ti}, wheretirepresents the assembly time of the assembly task with the task serial numberi;

p(i) is the immediate preceding task of taski;

q(i) is the next task of taski;

LEis the efficiency of assembly line;

SIis the smoothness index of assembly line;

(1)

2) Mathematical model

(2)

(3)

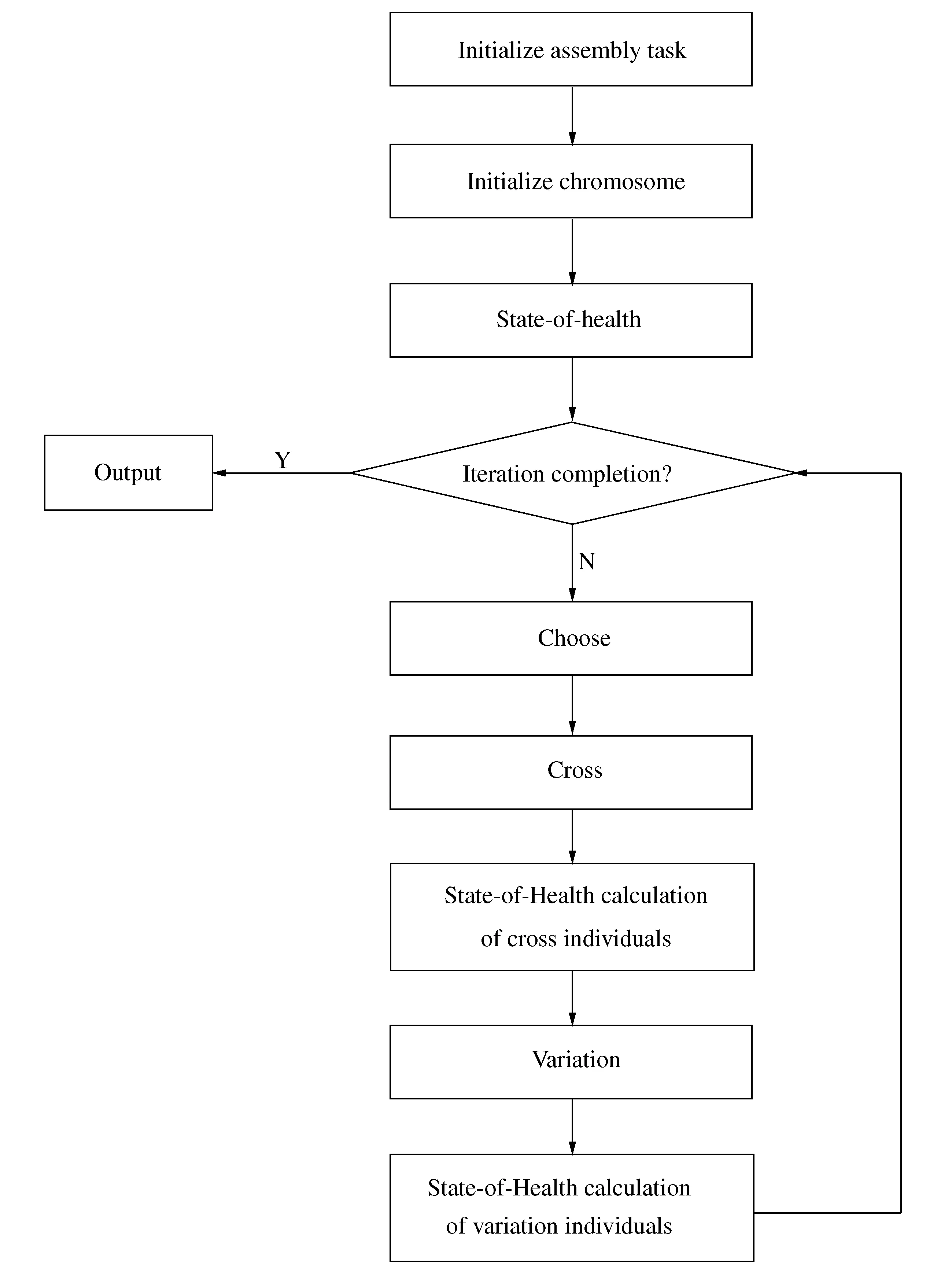
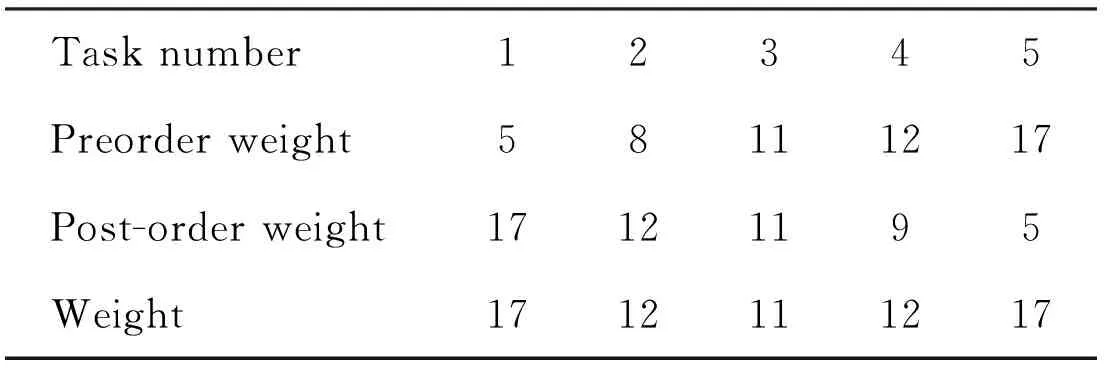
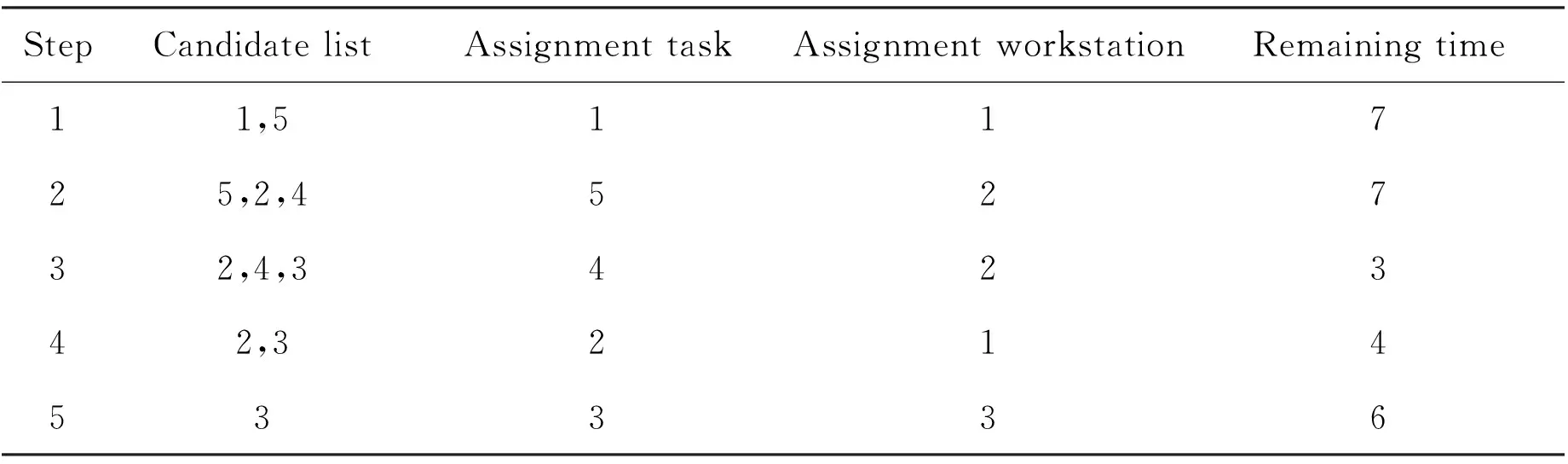
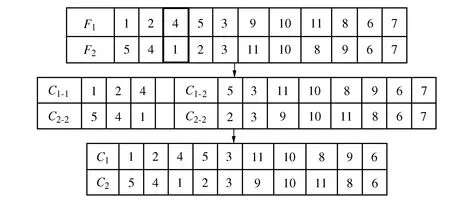
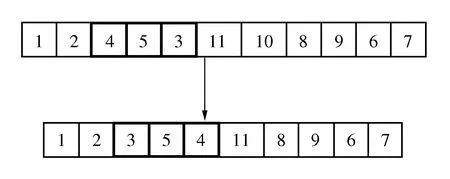
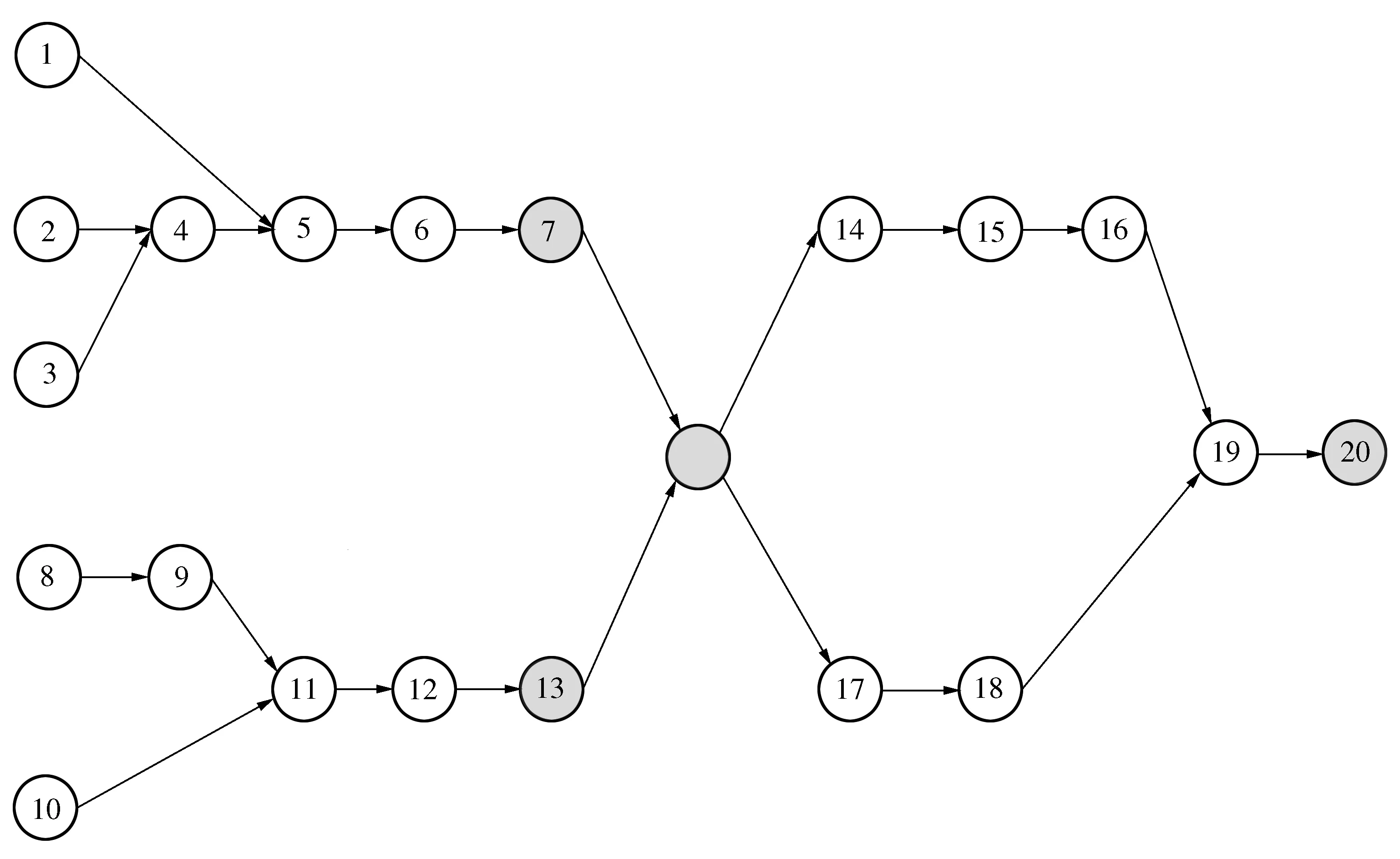
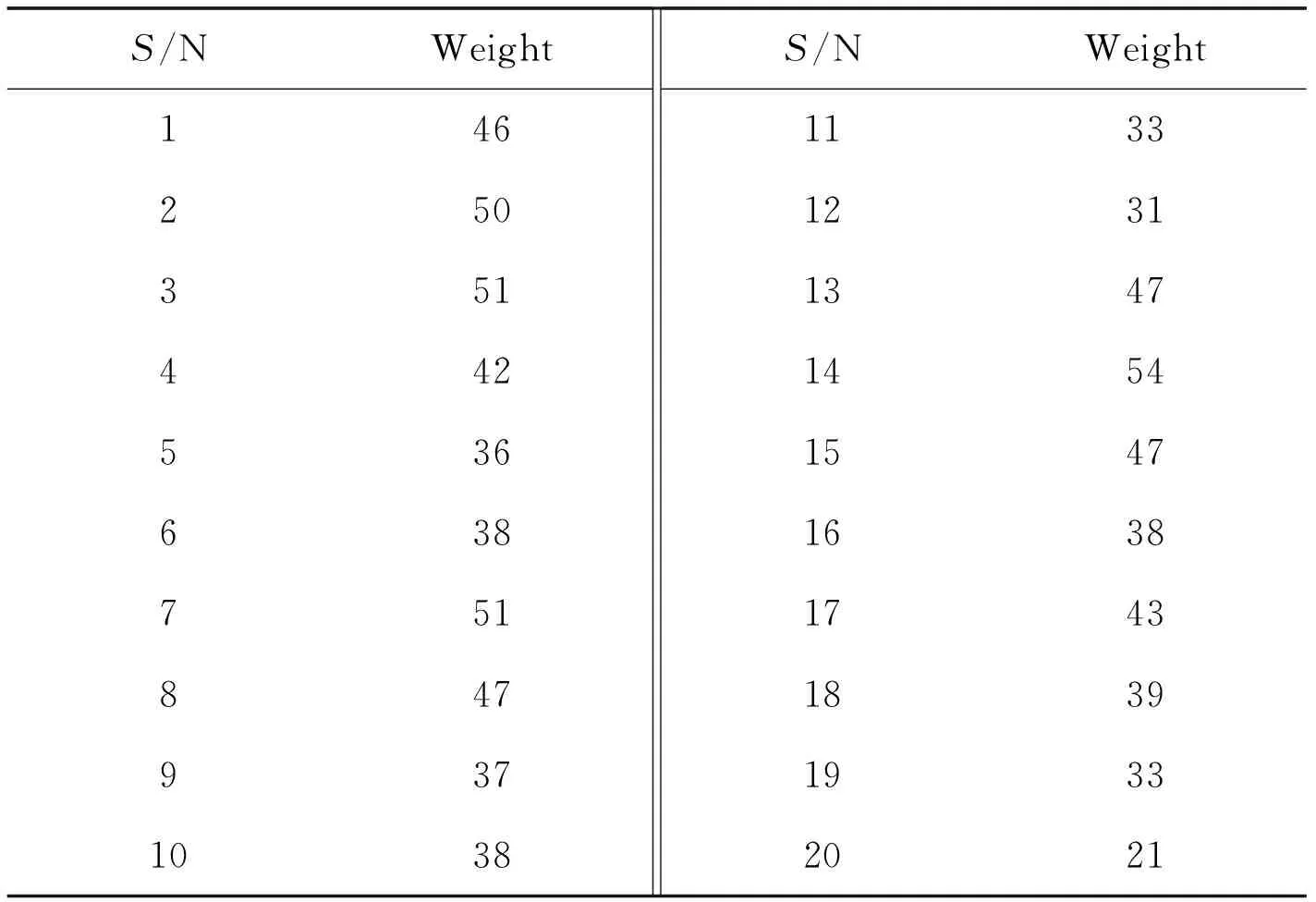
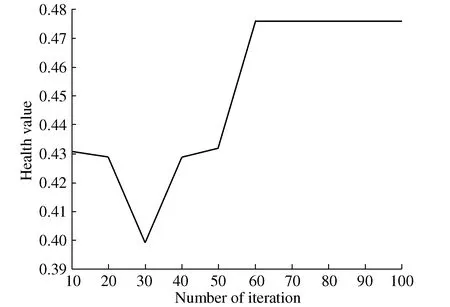
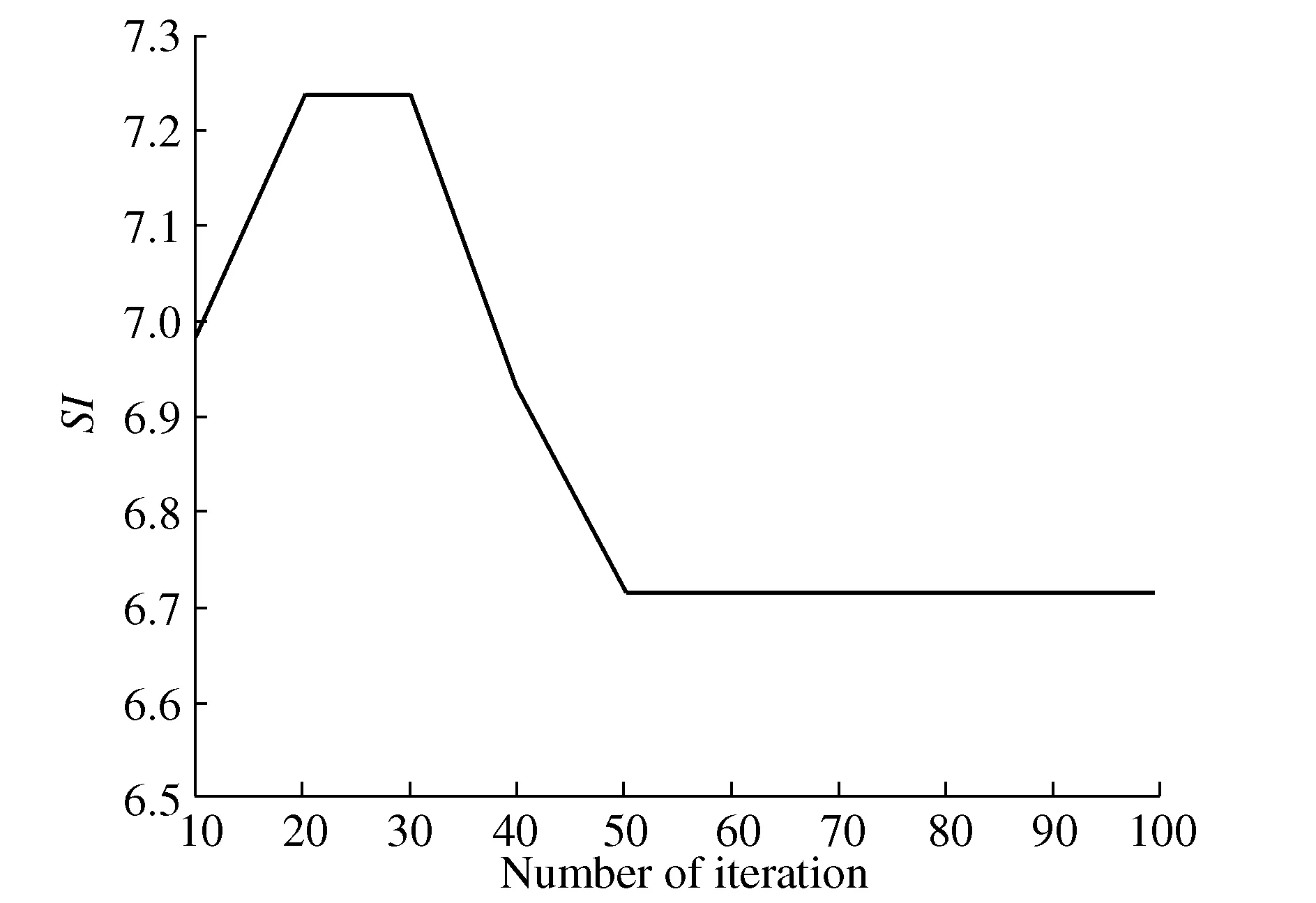
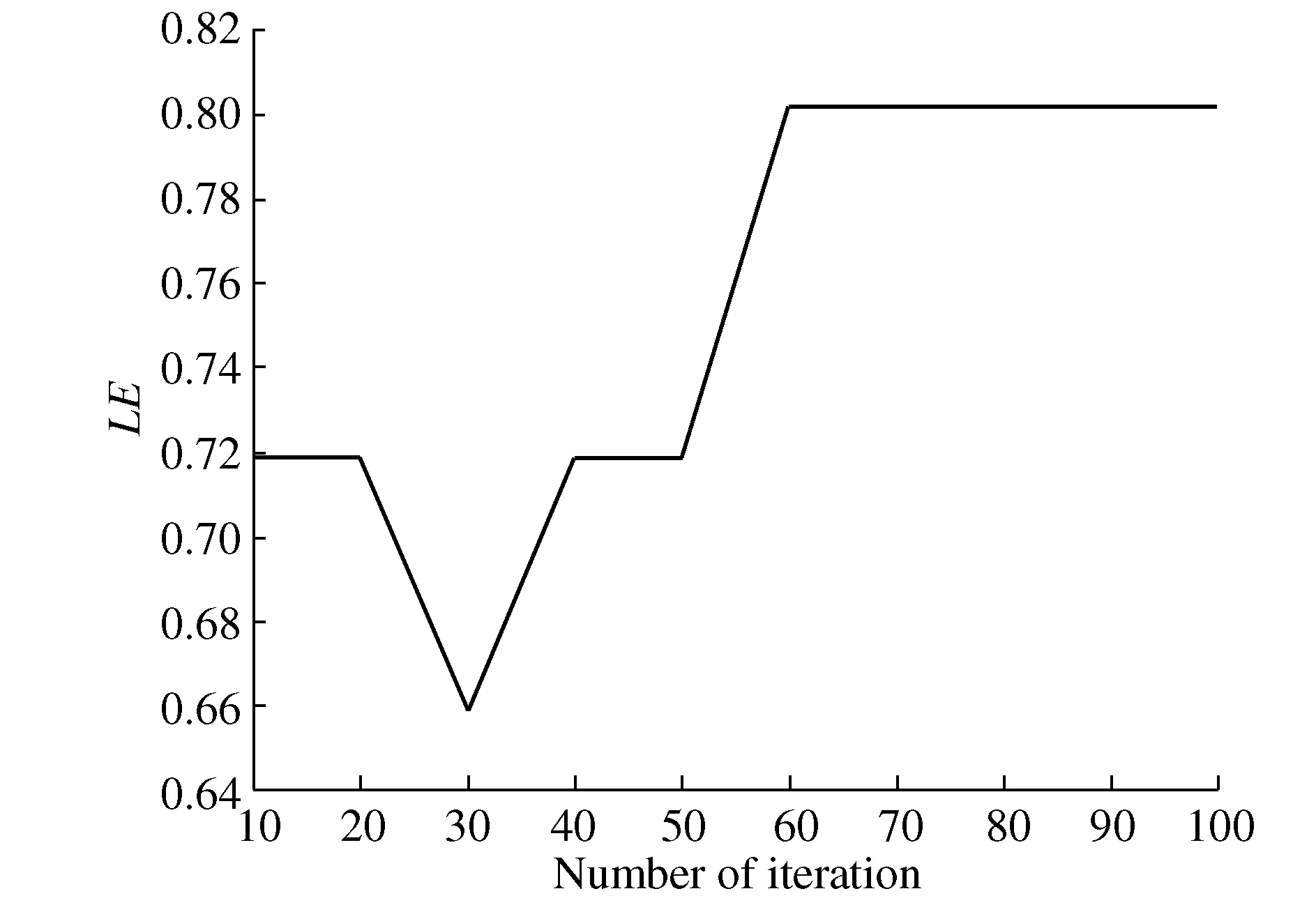
∑ti

0≤rti≤CT,∀j∈J,rti∈T

K(i,Q(I))∩K(P(i),i)=1

4 Genetic algorithm

Usually in the process of solving genetic algorithm, crossover probability operatorPcand mutation probability operatorPmare fixed values, which may have an impact on good individuals, because good individuals also have a certain probability of crossover and mutation. Therefore, this paper uses adaptive method to solvePcandPm, try to retain the best individuals while increasing the probability of poor individual crossover and mutation. The specific operation process is as follows:

(4)

(5)

Where:fmaxis maximum fitness of population;favgis population average fitness;f′ is the fitness value of the intersection of the two crossover individuals;fis variation individual fitness value;k1,k2,k3,k4are constants, and between 0-1.

In this paper,k1=1.0,k2=0.5,k3=1.0,k4=0.5. After using the adaptive crossover and mutation operator, each crossover and mutation requires the health of the individual, so after the crossover and mutation, the health of the newly generated individual needs to be calculated. The whole process of the algorithm is shown in Figure 5.

Figure 5 Genetic algorithm solution flow chart

4.1 Initial solution

When the genetic algorithm is used to solve the optimal allocation problem of assembly tasks, the chromosome is the set formed by the mapping of assembly tasks according to the allocation process. This mapping is the method of generating the initial solution. In this paper, the real number coding method is used to arrange each assigned task into a chromosome in turn, and a matrix containing block information and workstation information is also generated, as shown in Figure 6.

Figure 6 Chromosome example

The improved RPW method is used to solve the initial solution. Taking Figure 1 as an example, the specific operation is as follows:

Step 1: Divide the task into blocks.

Step 2: Take out the first block, calculate all task weights in the block, and get the task weights in Table 1.

Table 1 Task weight

Step 3: The tasks are arranged in order of weight from high to low.

Step 4: Randomly select one of the tasks with the highest weight and assign it to the first workstation.

Step 5: Select the task assignment from the remaining task sort table to each workstation. The allocation of subsequent tasks first finds the workstations that have been assigned their pre-order or post-order tasks according to the assembly task priority relationship matrix. If no sequential task has been assigned, it is assigned to the new workstation; if the sequential tasks have been allocated and the workstation meets the beat condition, it is randomly assigned to the workstation that meets the condition, otherwise it is assigned to the new workstation. Assuming that each workstationCT=12, the specific operation is shown in Table 2.

Table 2 Task allocation

Step 6: Form a chromosome fragment with the allocated block.

Step 7: Repeat steps 2-6 until all blocks are allocated.

Step 8: Splice all chromosome fragments into a complete chromosome in the order of blocks.

Step 9: Determine whether the chromosome already exists in the population. If it exists, restart the cycle of steps 2-9. If it does not exist, add it to the population until the initial population is generated.

4.2 Health calculation

Since the chromosome health is needed to calculate the operation probability in the process of crossover and mutation, it is necessary to recalculate the chromosome health after crossover and mutation. In the process of crossover and mutation, ifrtj≤0, the case is 0.

4.3 Selection

This paper uses roulette wheel method for population selection. The probability wheel is constructed by using the fitness of all individuals in the population. Finally, the offspring population is selected from the parent population pool by random selection.

4.4 Crossing

The crossover process plays an important role in the iterative process of genetic algorithm. Its essence is to exchange the partial structure of two parents to generate new individuals. Crossover is an important means to make excellent individuals appear in the population. In this paper, the method of order crossover is adopted. This method is improved on the basis of single point crossover, which can better retain the parent information and retain the existing constraint relationship and block relationship of the assembly line as much as possible. The chromosomal crossover is shown in Figure 7, and the specific operations are as follows:

Figure 7 Chromosomal crossover

Step 1: Calculate the crossover probability.

Step 2: Determine whether the cross operation.

Step 3: Generate the crossover point, select the left part of the chromosome of theF1crossover point as the partial chromosomeC1-1of the offspringC1, and the partial chromosome of theC2is the left part of theF2crossover point.

Step 4: The gene inC1-1was deleted fromF2, and the remaining part remained in the original order to formC1-2. Finally,C1-1andC1-2were spliced to formC1.

4.5 Mutation

The mutation operation can effectively avoid the local optimum in the iteration process of the genetic algorithm, so the larger mutation probability should be used as far as possible, but the excessive mutation probability will make the genetic algorithm become a random search algorithm. The adaptive mutation probability calculation used in this paper can effectively solve the above problems. The diagram of variation operation is shown in Figure 8, and the specific operations are as follows:

Figure 8 Diagram of variation operation

Step 1: Calculate mutation probability.

Step 2: Determine whether the mutation operation.

Step 3: Generate mutation points. If it is located at the edge of the block, the mutation point gene is exchanged with the adjacent gene position; if it is not located at the edge of the block, the gene positions on both sides are exchanged.

4.6 Optimal solution

In this paper, the solution with the highest health degree after a certain number of iterations is taken as the optimal solution.

5 Case experiment

In order to verify the effectiveness and reliability of the method, this paper takes a certain type of photoelectric component as the analysis object, and conducts a case study on the obvious blocks of its assembly process. The assembly relationship is shown in Figure 9. Among them, 7,13,20 three tasks represent detection work. Details of each assembly task and schedule is shown in Table 3, the weight of each task as shown in Table 4.

Figure 9 Assembly relationship diagram

Table 3 Assembly task details

Table 4 Assembly task weight

The number of blocks, the number of tasks contained in each block, the time consumption of each assembly task, the weight of tasks and other information are converted into a matrix and input into MATLAB. TheCTtime is set to 23, the iteration is set to 100 times, and the data is recorded every 10 times, as shown in Table 5.

Table 5 Optimal individuals and number of iterations

The three line charts of Figure 10, Figure 11 and Figure 12 show the health value, smoothness index (SI) and assembly line efficiency(LE) at different iterations. When the number of iterations is 10, the health value is 0.431,SIis 6.980, andLEis 0.719 4. When the iteration is completed, the health value is 0.476, the optimalSIvalue is 6.714, and the optimalLEvalue is 0.802 4.

Figure 10 Health degree

Figure 11 Assembly line smoothness index

Figure 12 Assembly Line Efficiency

From the above results, it can be seen that after using the improved genetic algorithm to optimize the assembly line, the smoothness and efficiency of the entire assembly line are at a better value, which can make the entire production smoother. In the actual production process, the typical photoelectric components of the assembly lineLEstatistics for 78.33%, less than 80.24%. And because do not pay attention to the assembly line load balance andSIis poor, usually greater than 9.0.

In addition, in actual production, there will be no fourth assumption in the design of mathematical models in this paper. However, due to the existence of a small U-shaped structure, the model in this paper is more flexible in repairing when problems are detected. Therefore, it is concluded that the assembly line scheme in this paper is better than the actual assembly line scheme.

6 Conclusion

In this paper, the construction mode of discrete assembly line of electronic products is studied. Firstly, the assembly line structure is heuristically adjusted according to the high assembly quality requirements of typical photoelectric component electronic products and the need to be assembled and inspected. After that, a mathematical model is established and an improved algorithm is designed for the characteristics of assembly task block. Then, the task of assembly line is allocated by algorithm in MATLAB, and the optimal method of assembly task allocation is obtained after iteration. Finally, compared with the actual production data, the feasibility of the algorithm optimization scheme in this paper is illustrated. In addition, considering the characteristics of the small U-shaped structure of the composite U-shaped assembly line proposed in this paper, it is concluded that this scheme is superior to the current assembly line scheme.