考虑多因素影响的无人机碰撞风险评估

童 亮,甘旭升,张宏宏,金剑勇

(1.空军工程大学 空管领航学院, 西安 710051;2.中国人民解放军95140部队, 广东惠州 516000)

0 引言

随着航空工业技术的快速发展,无人机凭借其机动能力强、成本低、风险小等特点,在军事、农业、交通等领域发挥越来越重要的作用。由于缺乏可靠的冲突解脱能力,无人机目前通常在隔离空域内运行[1]。融合空域是指无人机与有其他有人机同时运行的空域。为了保证无人机在融合空域执行任务的可靠性,降低对空域带来的不安全影响,需要对无人机碰撞风险概率进行评估[2]。

国内外对航空器飞行碰撞风险评估进行了一系列研究,最早用于碰撞风险评估的模型是Reich模型[3-4],分析了由于航空器位置误差造成的碰撞风险。EVENT模型用来评估纵向间隔与侧向间隔的碰撞风险[5]。石磊等基于三维布朗运动模型,计算出航空器碰撞概率[6]。王松涛等人综合考虑高空风等环境因素对碰撞概率的影响[7]。杨新湦以碰撞风险为量化指标,基于尾涡强度对无人机与民机的纵向安全间隔进行评估[8]。张宏宏为解决无人机在复杂低空环境内运行安全性较低的现状,提出了基于飞行环境的风险评估方法,为低空无人机航路规划方法提供参考[9]。谷志鸣利用蒙特卡洛对冲突解脱算法可靠性进行评估[10]。张兆宁提出基于考虑所需CNS(communication,navigation and surveillance)性能、防撞系统和高空风等影响因素作用下的碰撞风险评估[11]。

目前,国内外对民航客机之间的碰撞风险已有一定的研究,但是对融合空域内无人机避撞风险的研究相对较少。传统研究中,有人航空器之间的碰撞风险集中于考虑人为因素的影响,学者们从不同的角度、维度对人为因素的进行了定性、定量的阐述。无人机没有机载的飞行驾驶员对飞机进行直接操纵,缺乏有人机与有人机之间“看见即躲避”的避撞方式,使得融合空域内无人机与有人机在避撞过程中主要依赖于无线信号/指令的传输,无线信号/指令的传输过程中易受到多种环境因素的干扰,导致信号/指令出现中断、丢包等现象,进而影响无人机避撞行为的执行,从而引发相撞事故。无人机进入融合空域与有人机共同运行是一种趋势,尤其是无人机与民航班机在融合空域中的共同运行。因此,需要对无人机在融合空域内的碰撞风险评估进行深入研究。

本文针对无人机进入融合空域的现实需求,引入适用于无人机的速度障碍法模型。对融合空域内影响无人机与民航客机定位误差的关键因素构成与分布进行了分析。利用蒙特卡洛方法对经典冲突场景下的碰撞风险进行仿真,利用具体的理论数据得出无人机与有人机之间碰撞风险评估结果,为无人机进入融合空域提供一种理论参考。

1 无人机避撞模型

针对无人机在融合空域内避障问题,国内外学者将智能优化算法[12-13]、势场法[14-15]、几何法[16-17]等方法应用在冲突解脱领,均取得不错效果。Jérémy Omer[18]将基于时间离散的航迹优化算法和基于空间离散化的航迹优化算法以及单次调整的航迹优化算法进行了比较。从综合表现来说单次调整优化算法能够解决更为复杂的情况,并且算法得到的冲突消解机动产生的消耗较少,计算时间适中。因此,本文选取基于速度障碍法的集中式单次调整优化方法作为评估对象。

速度障碍法定义了一个障碍区域,当无人机与入侵障碍物的相对速度落在障碍区域之外,便可完成冲突解脱[19]。如图1所示,A与O点分别为无人机与动态障碍物的位置,速度分别为v1、v2,相对速度为v=v1-v2,无人机与障碍物之间的安全距离设为d1,无人机与障碍物之间的连线AO与v1、v2的夹角分别为θ1、θ2。无人机与障碍物之间的动态关系可转化成以相对速度vR运行的无人机与静止障碍物之间的关系。

图1 速度障碍模型示意图Fig.1 Diagram of speed barrier model

无人机可以通过改变航向与速度,使得相对速度vR落在速度障碍区之外,实现避障。

1.1 航向调整

如图2所示,无人机仅通过调整航向进行避障,无人机航向调整前后与坐标轴的夹角分别为θ1与θ′1,相对速度调整前后分别为vR与v′R,无人机速度调整前后分别为v1与v′1,则有,根据文献[20],冲突解脱过程中,无人机航向调整量Δθ1为:

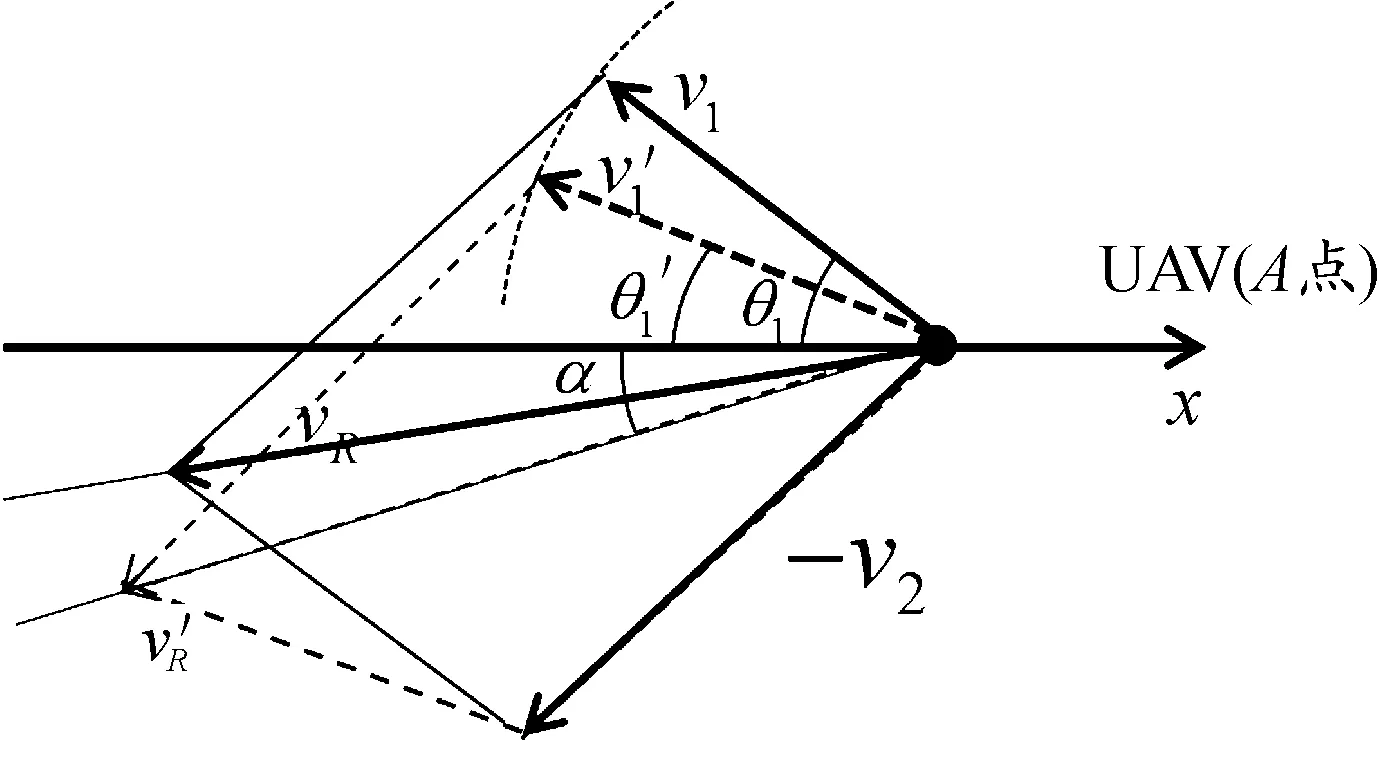
图2 无人机航向调整前后相对速度矢量示意图Fig.2 Schematic diagram of relative velocity vector of UAV before and after course adjustment

Δθ1=θ′1-θ1= arcsin(v2sin(θ2-α)/v1)-α-θ1

(1)

1.2 速度调整

如图3所示,无人机仅通过调整速度大小进行避障,根据文献[20],冲突解脱过程中,无人机速度调整量Δv1为:

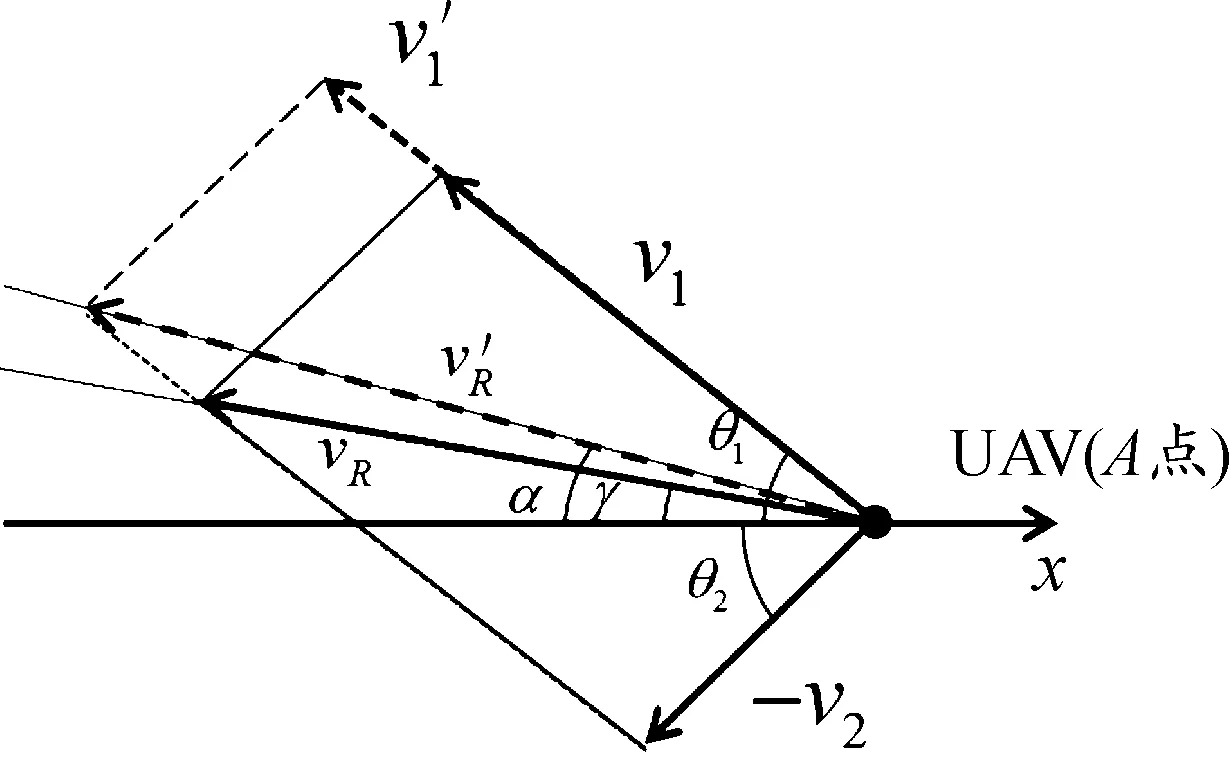
图3 无人机速度调整前后相对速度矢量示意图Fig.3 Schematic diagram of relative velocity vector of UAV before and after speed adjustment

Δv1=v′1-v1=v2sin(θ2+α)/sin(θ1-α)-v1

(2)

基于速度障碍法的集中式单次调整优化方法,无人机实现对障碍物规避并及时恢复到原航迹[20],效果较好,但假设过于理想,忽略了无人机运行不确定性因素对避障的影响,因此需要综合考虑影响因素,对碰撞风险进行评估。

2 无人机运行影响因素分析

无人机在融合空域内运行时,受到多随机因素影响,定位误差随着影响因素变化,造成一定程度的偏航,甚至导致无人机与空域内动态障碍物的危险接近、空中相撞,威胁无人机安全运行。本文选取影响无人机偏航的关键因素进行研究,假设造成无人机误差的各个环境要素之间相互独立,对多因素影响下的无人机碰撞风险进行评估。

2.1 导航性能对无人机定位影响

目前,无人机定位方式主要是采用GPS卫星导航,其误差来源主要有卫星误差、传播误差与接收误差。卫星误差主要包括星历误差、星钟误差以及相对论效应影响等,传播误差主要包括电离层延迟误差、对流层折射误差与多路径误差,接收误差主要包括接收机时钟误差、噪声误差与接收机天线相位中心误差[21]。GPS一般采用三星定位原理,除3个用于定位的卫星外,还需要一个原子钟,由第四个卫星代替,假设各个卫星对无人机定位影响相互独立,互不干涉。本文以P码编码方式为例,图4给出了各种误差来源造成的定位误差以及系统总误差[21]。

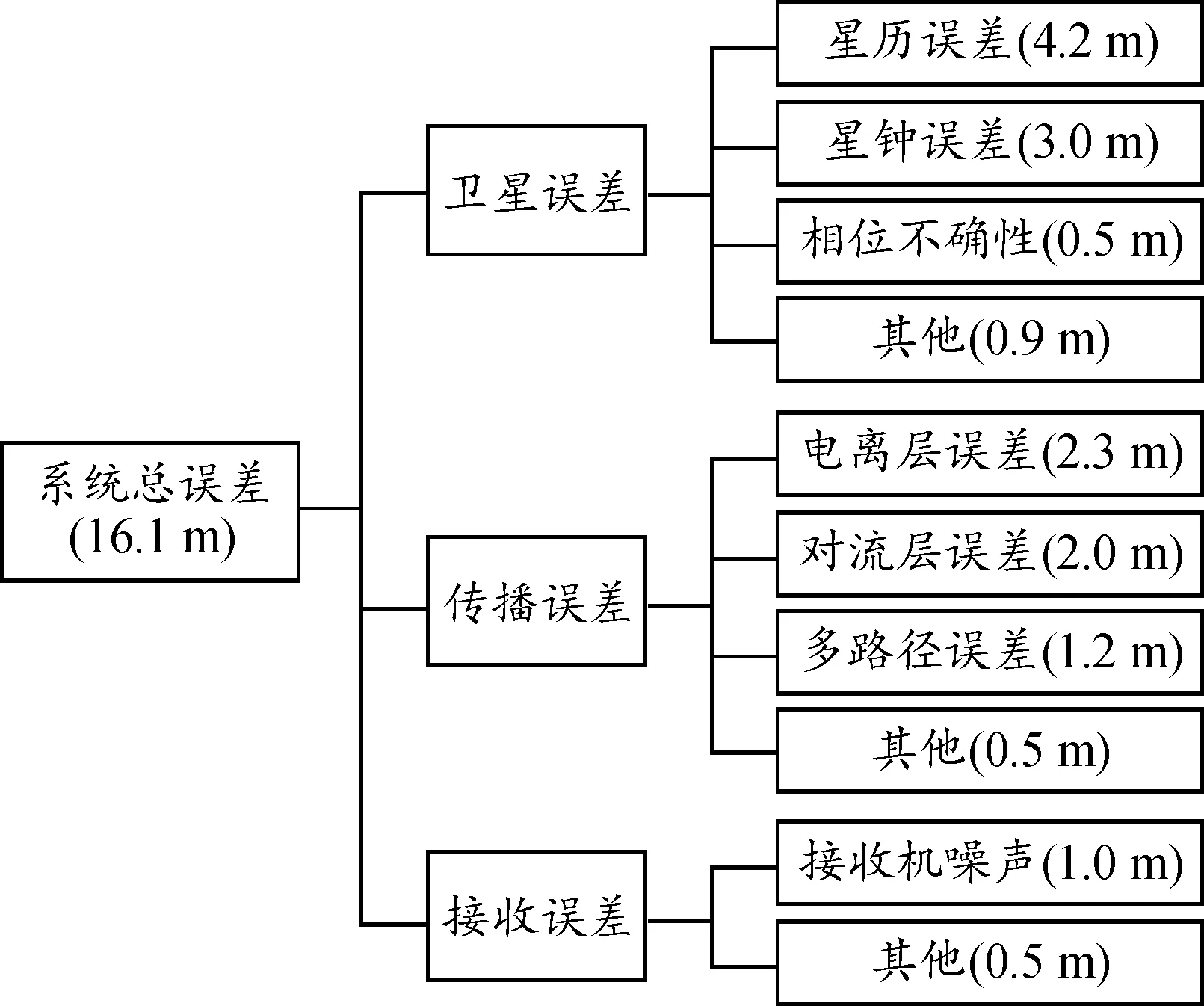
图4 各类误差对定位误差的影响Fig.4 The effect of various errors on positioning errors

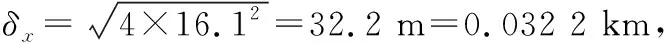
(3)

2.2 气象因素对无人机定位影响

空域内运行中的无人机极易受到不确定气象因素的影响,造成定位误差,假设无人机飞行所受顺风及逆风频率相同,无人机在高空风影响下的定位误差εw符合正态分布[22],密度函数表示为:

(4)

式中,μw与σw分别表示单独考虑气象因素(高空风)时,无人机定位误差的均值与方差。

2.3 无人机状态改变造成的位置误差

融合空域内的无人机通过改变航向或速度,实现冲突解脱,而在实际运行时,无人机航向与速度的改变并非瞬间完成,存在一定的延迟与位置误差。无人机系统的时间延迟不仅与机身操纵系统到响应时间、数据链信息传输延迟等因素有关,还与无人机地面站信息处理时间、链路上下传输延迟等因素有关[23]。

2.3.1改变航向时的定位误差

根据速度障碍法避障原理,无人机在AB航线上运行,到B点进行瞬间转向,再向BC方向继续运行。而实际运行的无人机受性能约束,为实现等效转向效果,需要在A点以P为圆心,为半径进行转向,运行到C点之后恢复直线航行,为理论转向角度,如图5所示。

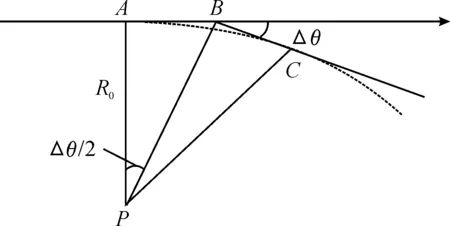
图5 无人机改变航向示意图Fig.5 Diagram of UAV changing course

由于无人机转弯时受到指令延迟、转弯速度等因素影响,无人机期望转弯角度与实际转角之间产生偏差,其实际的转弯角度Δθ′服从正态分布,概率密度表示为:

(5)

2.3.2改变速度时的定位误差

根据速度障碍法避障原理,无人机可改变自身速度大小实现避撞。实际无人机速度变化受自身性能约束,不可能瞬间完成变速,如图6所示,无人机运行速度由v1变为v′1时,飞行航程S为图中阴影面积,可表示为:

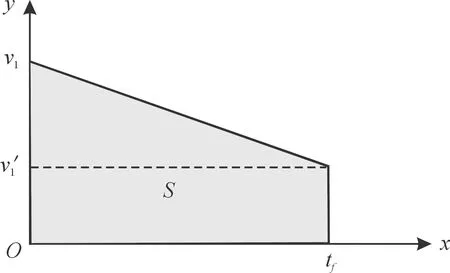
图6 无人机改变速度示意图Fig.6 Diagram of UAV changing speed

(6)

式中,tf为无人机变速结束时间,受自身性能约束,可表示为:

(7)

式中,amax为无人机最大加速度。

无人机按照最大加速度amax指令改变速度时,受到不确定性因素干扰影响,实际最大加速度amax服从正态分布,表示为:

(8)

式中,σa是加速度的方差,取0.01。

2.4 民航客机定位误差

无人机在融合空域内运行时动态障碍物类型众多,这里选取民航客机作为动态障碍物,无人机通过执行避撞策略实现冲突解脱。根据文献[11],运行中的航空器由于定位误差,会偏离理论航行路线,造成碰撞风险。民航飞机导航误差通常由导航精度引起的,密度函数服从期望值为0的双指数分布,可表示为:

(9)

式中:a为位置参数,b为尺度参数且b>0,二者为偏航误差概率密度中的参数。

根据所需导航性能(required navigational performance,RNP)定义,RNPn指航空器在n海里之内,以95%的概率偏离航线的距离[11]。则有:

(10)

3 仿真分析

为验证速度障碍法避障的有效性,本节运用环境进行仿真,其中无人机与民航飞机的初始位置、航向与运行速度给定,应用蒙特卡洛算法,分析运行中的不确定性因素对避障算法的影响。根据无人机运行特点,无人机安全圆半径设为15 km,机载传感器探测半径设为100 km。

相对于巡航阶段,民机进离场与起降阶段时飞行高度较低,也是与无人机发生冲突,产生危险接近最多的阶段。本文构建的冲突场景为无人机与进离场与起降阶段时民航客机航线交叉相遇下的冲突解脱场景,结合我国航空器飞行间隔标准,根据航空器运行最小间隔距离,对碰撞风险进行分类评估[24],如表1所示,当两机最小间隔距离小于1.76 km时,定为严重事故,当两机最小间隔距离处于1.76～3 km时,定为危险接近,当两机最小间隔距离处于3～10 km时,定为飞行冲突,当两机最小间隔距离处于10～15 km时,定为存在风险,当两机最小间隔距离大于15 km时,定为安全运行。

表1 事故风险等级划分Table 1 Classification of accident risk levels

3.1 冲突场景仿真

选取大型无人机与民航航机作为碰撞对象,融合空域内不确定因素参数具体数据如表2所示。无人机与民航客机初始信息如表3所示。

表2 所需参数值Table 2 Required parameter value

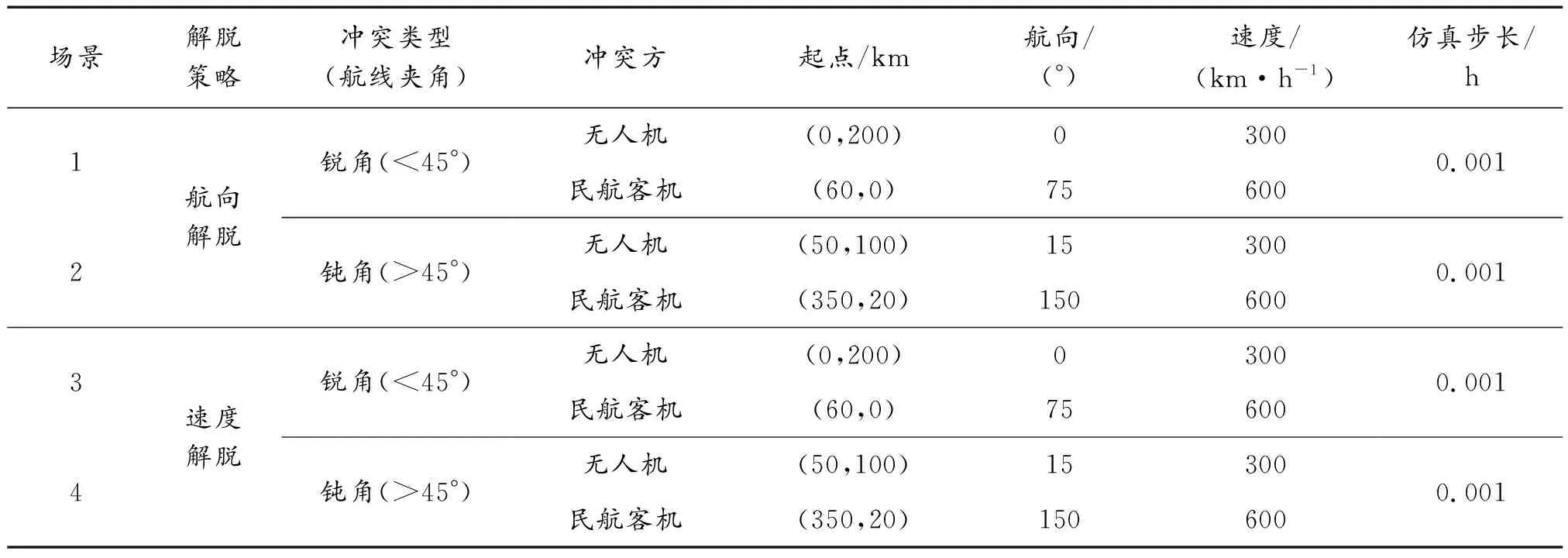
表3 无人机与民航客机初始信息Table 3 UAV and civil aircraft initial information

场景1、场景2分别为无人机任务航线与民航客机航线夹角分别为锐角、钝角的冲突场景,根据速度障碍法避障策略,无人机通过单独调整航向,改变无人机与民航客机之间的相对速度,实现融合空域内的避撞。场景1中无人机与民航客机之间的理论航迹图、双方理论间隔与实际间隔分别如图7所示。

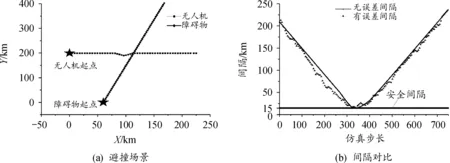
图7 场景1仿真示意图Fig.7 Scenario 1 simulation diagram

场景3、场景4分别为无人机任务航线与民航客机航线夹角分别为锐角、钝角的冲突场景,根据速度障碍法避障策略,解脱策略采用速度解脱,无人机通过单独调整速度大小,改变无人机与民航客机之间的相对速度,实现融合空域内的避撞。场景3中无人机与民航客机之间的理论航迹图、双方理论间隔与实际间隔分别如图8所示。

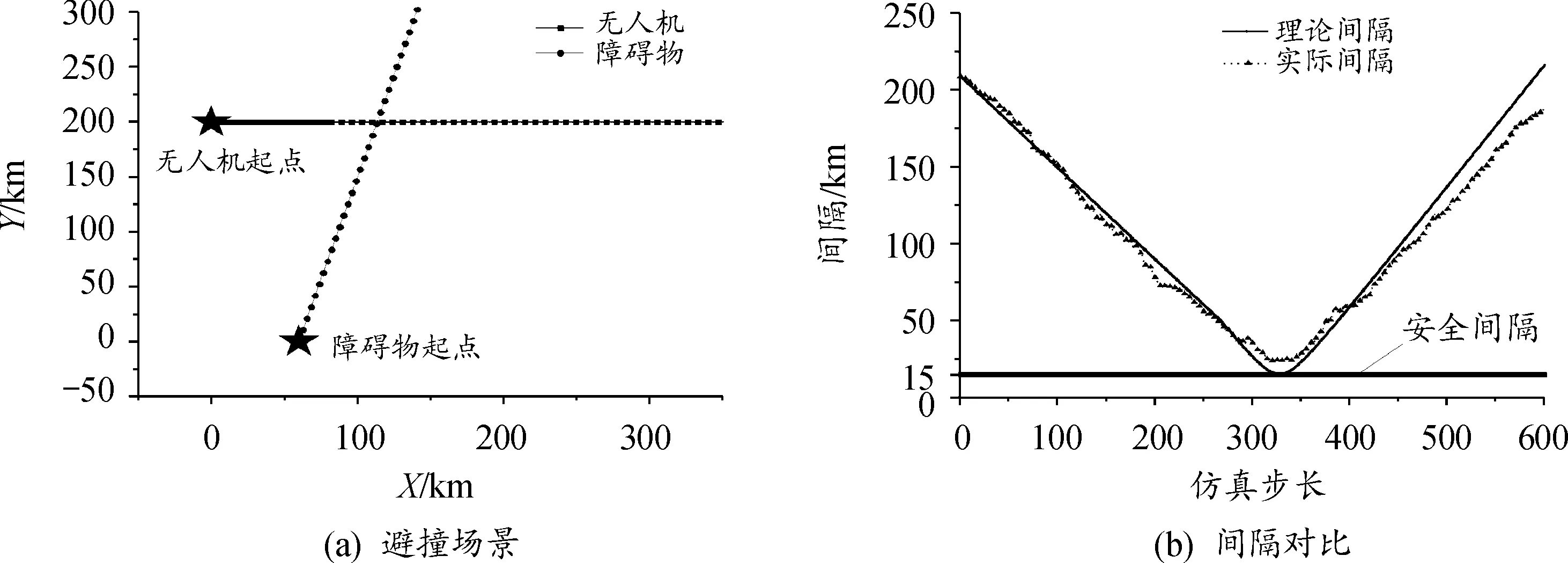
图8 场景3仿真示意图Fig.8 Scenario 3 simulation diagram

场景2、场景4避撞场景、间隔对比仿真图与场景1、场景3类似,限于篇幅不再罗列。

采用蒙特卡洛仿真模拟,对场景1～场景4分别进行10万次重复实验,统计无人机与民航客机之间的风险等级分别处于严重事故、危险接近、飞行冲突、存在风险、安全运行等5个等级下的发生次数,具体数据如表4所示,分布如图9所示。

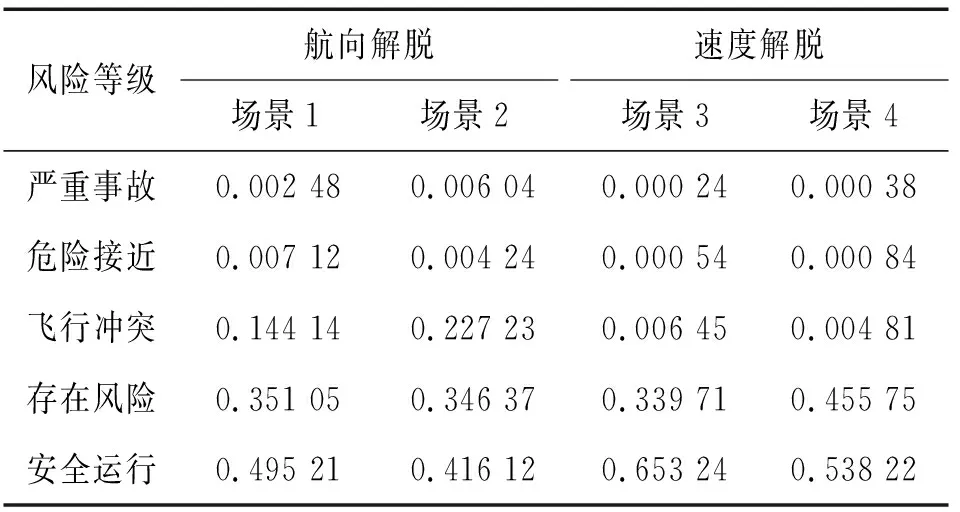
表4 不同场景下事故率统计Table 4 Accident rate statistics under different scenarios

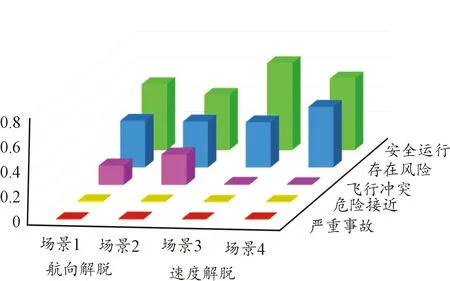
图9 不同场景下事故率分布Fig.9 Accident rate distribution under different scenarios

分析场景1～场景4中各风险等级发生概率,可以发现航向解脱与速度解脱2种策略在一定程度上均能避免无人机与民航客机之间的严重事故,但离国际民航组织提出的有人机总体安全目标水平(target level of safety,TLS)次事故/飞行小时还有一定差距;同时在同等误差条件下,速度解脱策略造成的严重事故往往更低,因此在同等冲突场景下,应优先选择速度解脱策略进行避撞。

3.2 民航客机定位误差对安全目标水平的影响

为更精确描述民航客机定位误差对安全目标水平的影响程度,针对场景1,保持其他误差参数不变,对不同RNP性能环境下的避撞效果进行仿真,如图10所示,无人机与民航客机的碰撞严重事故率随着避撞间隔的增大而降低,同时,民航客机导航性能越精确,达到同等安全目标时所需的避撞间隔越小。

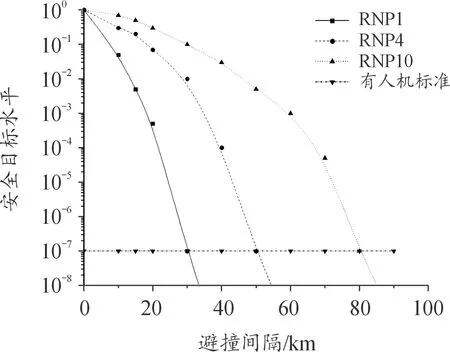
图10 民航客机定位精度对安全目标水平的影响Fig.10 Influence of positioning accuracy on safety target level of civil aircraft

3.3 无人机转向误差对安全目标水平的影响

将无人机转向误差方差值σ分别设为0.05、0.01与0.15,对在3种转向误差下的无人机安全目标水平进行实验,得到如图11所示结果,仿真结果表明:在合理误差下,无人机转向误差对安全目标水平影响程度较小。

图11 无人机转向误差对安全目标水平的影响Fig.11 Influence of UAV steering error on safety target level

3.4 高空风影响下的定位误差对安全目标水平的影响

选取高空风影响下的定位误差为研究对象,分别研究物理量在σ、2σ、3σ下的误差,具体分布如图12所示。可知,同一避撞间隔下,定位误差取值增大,安全目标水平的取值相应增大,安全性越低;随着避撞间隔的增大,安全目标水平取值减小,安全性提高。

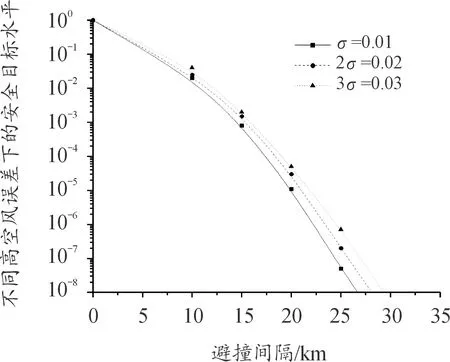
图12 不同高空风误差下的安全目标水平示意图Fig.12 Safety target level diagram under different upper air wind errors

3.5 无人机碰撞间隔设置

目前,无人机与民航客机之间的安全间隔距离暂无明确标准,本文将安全间隔距离分别设为10～20 km,以场景1为研究对象,在同等误差条件下进行1 000万次蒙特卡洛仿真,各安全间隔下的严重事故发生概率如图13所示。可以看出,无人机与民航客机发生严重事故概率随安全间隔的增大而减小,当安全间隔变为25 km左右时,严重事故发生概率大约与有人机总体安全目标水平(次事故/飞行小时)相等,为无人机融入有人机空域的安全间隔设置提供了评估方式。

图13 严重事故概率变化趋势Fig.13 Trend of serious accident probability

4 结论

当前国内外对无人机在融合空域内冲突解脱技术的研究较多,实验案例往往仅验证解脱算法的有效性,很少有从安全性的角度对解脱算法进行考虑,并且目前对融合空域内无人机运行安全评估体系还很缺乏。因此,利用蒙特卡洛技术对无人机与民航客机的冲突解脱算法进行大规模仿真,得到如下结论:

1) 航向解脱与速度解脱2种策略在一定程度上均能避免无人机与民航客机之间危险接近,避障间隔设置越小,离国际民航组织提出的有人机总体安全目标水平差距越大。在同等误差条件下,速度解脱策略造成的严重事故往往更低,因此在同等冲突场景下,应优先选择速度解脱策略进行避撞。

2) 无人机与民航客机的碰撞严重事故率随着避撞间隔的增大而降低,同时,民航客机导航性能越精确,达到同等安全目标时所需的避撞间隔越小。在合理误差下,无人机转向误差对安全目标水平影响程度较小。

3) 无人机与民航客机发生严重事故概率随安全间隔的增大而减小,当安全间隔设为25 km左右时,严重事故发生概率大约与有人机总体安全目标水平相等,为无人机与障碍物、电子围栏安全间隔的设置提供了一种理论计算方式。