多层复合回音壁微腔热振荡效应的理论研究
程肯 王铁军


摘 要 多层复合材料微腔能够观察到单一材料无法实现的独特现象。本文在理论上分析了由丝状蛋白和聚二甲基硅烷(PDMS)涂覆的二氧化硅微球腔热振荡效应,并观察到该复合回音壁微腔独特的振荡波形。该波形由两个不同速度的振荡周期组成,在慢速的振荡周期中包含着若干快速的振荡周期,并且快速的振荡只出现在丝状蛋白和二氧化硅的温度上升区间。我们基于耦合模理论构建的热动力学方程解释了这一现象。这种双频振荡同时出现的现象在传感器领域有着潜在应用价值。
关键词 回音壁模式;微球腔;热振荡效应;复合材料
基于回音壁模式的光学谐振器越来越得到人们的重视,因为其能通过连续的内反射将光囚禁在微腔中,从而达到增加内部场强的效果。回音壁模式光学微腔从结构上来说可分为微球腔、微环腔和微泡腔等。基于这些特性,目前研究人员已经在分插滤波器[1,2]、生物分子感测[3]、微激光器[4]、腔量子电动力学[5]等方面进行了深入研究。
回音壁光学微腔具有较高的品质因子和较低的模式体积,能极大增强微腔内的光场能量密度,产生丰富的非线性效应现象。在各种光场形成的非线性效应中,最为常见的便是热非线性效应[6-8],包括热双稳态[9]和热振荡。一方面,热光非线性效应会带来器件的不稳定;另一方面,基于热光效应的非线性特性具有某些重要的实际应用价值[10]。值得注意的是,当谐振器中采用具有多种热光特性的材料时,将会出现更多有趣的现象。近十年来,对微腔内部通过两种或两种以上效应相互竞争而产生的周期性自激振荡的研究已相当深入。到目前为止,已经在未涂覆的单一材料观察到非线性热振荡现象,例如二氧化硅微球体[11]、氟化钡微盘腔[12]和近来新兴的铌酸锂微盘腔[13]中。除此之外,在带有涂覆层的复合微腔中也观察到了类似的现象,例如涂有聚二甲基硅烷涂层的微环芯腔[14]、涂有聚甲基丙烯酸甲酯涂层的微盘腔[15]以及丝状蛋白涂覆的微球腔[16]等。
为了填补双层以上复合回音壁微腔热振荡效应的研究空白,我们在理论上提出了一种复合三层回音壁微球腔(二氧化硅丝状蛋白PDMS)。
我们基于耦合模理论和热光动力学方程构建了相应的模型,并使用龙格库塔法进行理论仿真。理论分析发现其透射谱波形不同于以往研究中所独特的现象,该输出谱振荡波形由快慢两个振荡周期组成,存在着慢速的振荡中包含快速振荡的“双频振荡”。这种特有现象是由于聚二甲基硅烷材料相对于丝状蛋白材料具有更高热敏性,因此在丝状蛋白完成一个振荡周期的时间内,泵浦光能推动聚二甲基硅烷层中完成多次振荡。该模型表明透射谱可以同时表征两种振荡频率,在传感器和光学调制中可能具有重要应用。
1 理论模型
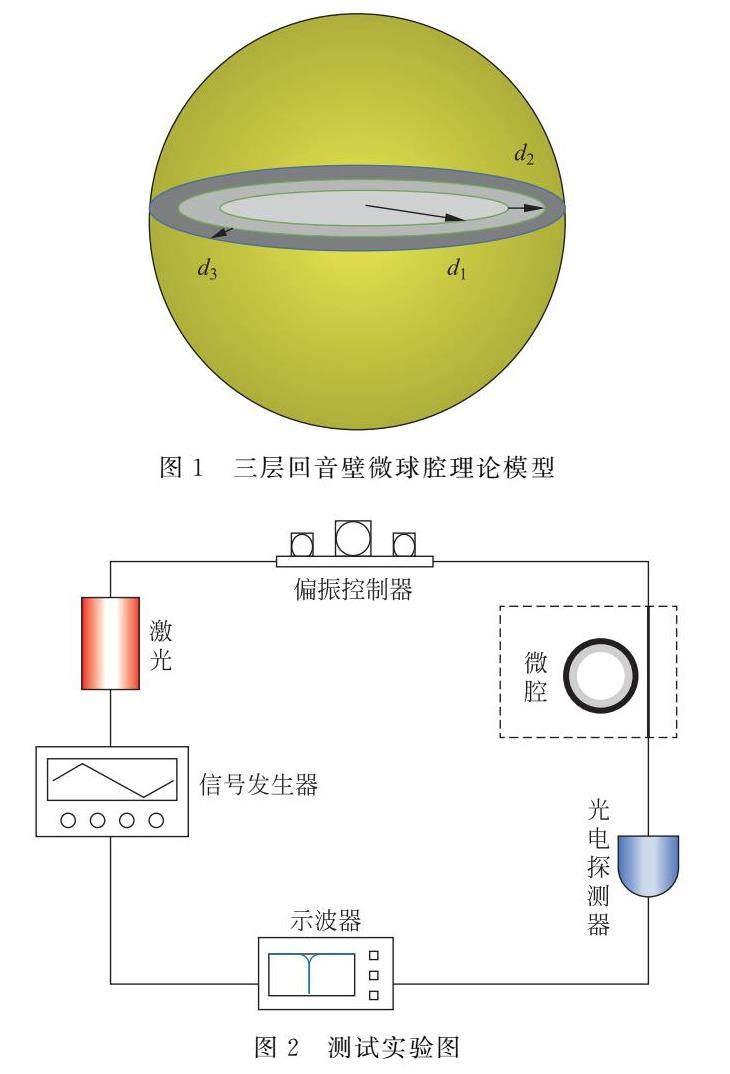
本部分我们将根据耦合模理论和热动力学方程来表征系统的透射谱。图1为横截面示意图。我们所使用的多层复合谐振器由内部为二氧化硅微球腔腔(如图1横截面白色区域所表征,半径d1 =21μm)的外面渡上一层(厚度d2=30nm)絲状蛋白夹层组成,然后再在该双层复合微球腔的基础上渡上一层(厚度d3 =30nm)聚二甲基硅烷(PDMS)的外层(如图1横截面深灰色区域所表征)。
理论上,我们设计的实验原理图如图2所示。泵浦光从激光器射出后经过偏振控制器来使其进入偏振状态。我们通过光纤锥耦合的方式将光耦合进微腔中,当有泵浦光通入光纤后,在锥形区域会产生倏逝波,这样就能实现与微腔的耦合。随后,透射光被光电探测器探测,其透射谱成像于相连的示波器上。
聚二甲基硅烷和丝状蛋白具有很好的透光性,且其透射率和二氧化硅相近,因此三层回音壁微腔与锥形光纤形成的耦合系统与常见的微球腔与锥形光纤耦合系统原理相同,其原理如图3所示。
在 这个基本光纤锥和微腔耦合的系统中,a t 表示微球腔内回音壁模式的光强,ain、ao 分别光纤内输入和输出的光强,k 为微腔和光纤的耦合系数,t 表示光纤和微腔中光的透过系数,我们得到微球腔内的模动力学方程为
2 数值模拟结果与分析
经过数值拟合得到的透射谱、温度变化和谐振波长的变化关系如图4所示。
我们可以看到三层回音壁微腔的振荡波形呈现出快速和慢速相结合的现象。慢速的振荡波形与仅包含丝状蛋白和二氧化硅的双层微腔的振荡波形相似,并且每一个快速的振荡波形也间断式出现,快速振荡周期数逐步增加,这个可以解释为热膨胀效应(二氧化硅的正效应与丝状蛋白的负效应相互竞争)和热光效应(二氧化硅的正效应和其他两个涂层的负效应相互竞争)以及考虑了二氧化硅的快慢两个散热过程,产生了不同时间跨度内不同的振荡效应。下面对谐振波长式(5)三层中各自的热振荡效应影响冷腔波长的系数进行分析。如图4(d)(e),快速振荡周期主要和聚二甲基硅烷的热振荡效应有关,而对于仅考虑内部两层的热光效应和机械延展效应基本遵循的振荡波形时,最外层的涂覆层对其他两层的热振荡影响较小。同时,从图4(d)表明,快速的热振荡效应间断性出现,且只出现在慢速振荡周期的一侧。下面我们截取两个周期进行系统分析。
从图4(d)(e)图中可以知道,二氧化硅层的正热光效应推动谐振波长红移,丝状蛋白层中的热膨胀效应和丝状蛋白、PDMS中的负热光效应推动谐振波长蓝移。若前者效应强于后者,则谐振波长整体增加,反之,则减小。由于聚二甲基硅烷对温度的敏感性要高于丝状蛋白,且热吸收系数高于后者两个量级以上,因此能够在内部两层完成一个慢速振荡周期中的温度上升阶段便完成多个快速振荡周期,类似聚二甲基硅烷与二氧化硅双层耦合模型中的整个振荡过程[14]。当谐振波长增加得比扫描波长增加的速度快时,失谐量开始增加,透射谱回升,腔内的能量减少,直至腔内的能量不足以推动腔模的温度继续升高时,二氧化硅与丝状蛋白中的温度开始降低;PDMS和丝状蛋白下降速度比二氧化硅快得多,没有了二氧化硅中的正热光效应的推动,腔内的振荡就在短时间内不能产生,这就是在慢速振荡周期的下降部分不能产生快速振荡的原因。由于之前腔模已经积累了较大的温升,支持谐振波长持续增长,这导致每个慢速振荡周期越长,也就为聚二甲基硅烷产生更多的快速振荡提供了条件。同时,随着反应的进行,在第五个慢速振荡周期中(见图5(d)) 会出现一个无振荡的真空期,其原因是模式体积内积累足够的能量,温度越高,丝状蛋白模式体积内的温度上升速度也就越快。随着丝层的升温速度快到一定程度后其负效应导致谐振波长虽然稍有增加但失谐量无法增加很多反而开始减小。此时PDMS层的温度保持稳定,当腔内的能量不足以支持丝状蛋白的吸收速率时,丝状蛋白的温度升高速度开始趋缓,谐振波长也开始由于耦合进腔内的能量逐渐减少,失谐量逐步增加,直至下一个快速振荡周期开始。在第六个慢速振荡周期中,当吸收功率不再能满足二氧化硅的热耗散时,失谐量逐渐增大,此后丝状蛋白和PDMS的能量快速耗散掉,相对体积更大、积累更多能量的二氧化硅的温度会缓慢减小。图5为截取第一个和第五个振荡周期的理论结果图。
3 结语
本文研究了该复合回音壁微腔内的热振荡效应,发现由二氧化硅、丝状蛋白和聚二甲基硅烷所组成的复合微腔能够实现两种振荡周期并存的热振荡效应。我们构建了相应的热力学方程,并尝试解释了整个物理过程来探讨产生这种独特机制的原因,发现每个慢速的振荡周期都包含着逐渐增多的快速振荡周期,并且快速振荡周期只出现在慢速振荡周期的上升过程。下一步,我们将在实验上验证这一理论模型。该复合回音壁微腔模型理论上能同時表征两个振荡频率,在传感器、光学开关和光学调制方面有着潜在应用价值。
致谢: 感谢刘晓斐博士对本文提供的帮助;本论文受到国家自然科学基金项目(62071064)和北京邮电大学研究生专业课程建设教革项目(2022ZY119)的资助。
参 考 文 献
[1] MANOLATOU C, KHAN M J, FAN S, et al. Coupling ofmodes analysis of resonant channel add-drop filters[J].IEEE Journal of Quantum Electronics, 1999, 35(9):1322-1331.
[2] CHU S T, LITTLE B E, PAN W, et al. An eight-channeladd-drop filterusing vertically coupled microring resonatorsover a cross grid[J]. IEEE Photonics Technology Letters,2002, 11(6):691-693.
[3] ZHU J, OZDEMIR S K, XIAO Y F, et al. On-chip singlenanoparticle detection and sizing by mode splitting in an ultrahigh-Q microresonator[J]. Nature Photonics, 2010,4(122): 46-49.
[4] VOLLMER F, ARNOLD S. Whispering-gallery-mode biosensing:label-free detection down to single molecules[J].Nature Methods, 2008, 5(7):591-596.
[5] SPILLANE S M, KIPPENBERG T J, VAHALA K J, et al.Ultra-high-Q toroidal microresonators for cavity quantumelectrodynamics[J]. Phys.Rev.A, 2005, 71(1): 013817.
[6] KIPPENBERG T J, SPILLANE S M, VAHALA K J.Kerr-Nonlinearity Optical Parametric Oscillation in an Ultrahigh-Q Toroid Microcavity[J]. Physical Review Letters,2004, 93(8): 083904.
[7] CHAI C Z, HU X X, ZOU C L, et al. Thermal bistabilityof magnon in yttrium iron garnet microspheres[J]. AppliedPhysics Letters, 2019, 114(2): 021101.
[8] PADMARAJU K, BERGMAN K. Resolving the thermalchallenges for silicon microring resonator devices[J]. Nanophotonics,2014, 3(4-5): 269-281.
[9] CARMON T, YANG L, VAHALA K. Dynamical thermalbehavior and thermal self-stability of microcavities[J]. Opticsexpress, 2004, 12(20): 4742.
[10] ANDRONICO A, FAVERO I, LEO G. Difference frequencygeneration in GaAs microdisks[J]. OpticsLetters,2008, 33(18): 2026-2028.
[11] PARK Y S, WANG H. Regenerative pulsation in silicamicrospheres[J]. Optics Letters, 2007, 32(21):3104-3106.
[12] DIALLO S, LIN G, CHEMBO Y K. Giant thermo-opticalrelaxation oscillations in millimeter-size whispering gallerymode disk resonators[J]. Optics Letters, 2015, 40(16):3834-3837.
[13] WANG J, ZHU B, HAO Z, et al. Thermo-optic effects inon-chip lithium niobate microdisk resonators[J]. OpticsExpress, 2016, 24(19):21869-21879.
[14] HE L, XIAO Y F, ZHU J, et al. Oscillatory thermal dynamicsin high-Q PDMS-coated silica toroidal microresonators[J]. Optics Express, 2009, 17(12):9571-9581.
[15] DENG Y, LIU F, LESEMAN Z C, et al. Thermo-optomechanicaloscillator for sensing applications[J]. OpticsExpress, 2014, 21(4):4653.
[16] LIU Y, JIANG X, WANG C, et al. Optothermally inducedmechanicaloscillation in a silk fibroin coated high- Qmicrosphere[J]. Applied Physics Letters, 2020, 116(20):201104.
[17] 王全龙. 回音壁模式光学微腔热非线性效应及其折射率调制特性[D]. 长春:中国科学院研究生院(长春光学精密机械与物理研究所), 2015.

