装药长径比对杆式射流成型与侵彻性能影响的数值模拟研究

杨世全，王守乾，冯高鹏

(中国工程物理研究院总体工程研究所，四川 绵阳 621999)

0 引言

杆式射流又称聚能杆式侵彻体或高速杆式弹丸,是一种侵彻性能介于聚能射流和射弹之间的侵彻体,相比传统聚能射流,具有对炸高不敏感,药型罩利用率高,可形成更大开孔口径等优点;相比爆炸成型弹丸,具有飞行速度更高、长度更长、截面动能比更大、侵彻能力更强等优点,因此在对付一些装甲防护、砖墙和钢筋混凝土等目标的攻坚弹药上具有较好的应用前景[1]。国内相关学者[2-10]针对杆式射流成型及侵彻性能采用理论分析、数值模拟和试验验证的方式开展了大量研究,重点分析了不同药型罩构型以及起爆方式和起爆精度等对最终结果的影响,获得了一些规律性认识。但由于影响杆式射流成型和侵彻性能的因素包括药型罩材料、罩型、装药结构以及起爆方式等诸多因素,且各因素之间的许多细节问题尚未完全认识清楚。理论分析提供了一种简便快捷的分析方式,但分析时往往基于一定的假设,缺乏对问题的直观认识。试验方式可获得问题的直观认识,也被认为是研究问题的有效途径,但其周期长、投入高,且很难单纯的从试验结果对问题进行深入的分析。因此数值模拟杆式射流成型及对目标靶体的侵彻过程,并结合一些关键过程参量的变化对结果进行深入的分析就成为问题研究的主要途径。

在装药长径比对杆式射流成型及侵彻影响研究方面,李伟兵等[11]运用LS-DYNA软件模拟了聚能杆式侵彻体的成型,并通过X光成像试验进行了验证,获得了侵彻体飞行稳定性较佳的装药长径比。张万君等[12]运用LS-DYNA软件的二维多物质纯ALE算法,建立不同装药长径比有限元模型,数值模拟了6种不同装药长径比的半球形聚能装药产生射流的过程,获得了射流不易断裂、均匀性较好的装药长径比。崔魁文等[13]基于一种球锥形药型罩,运用AUTODYN软件开展了聚能杆式侵彻体成型的数值模拟,分析了装药长径比对杆式射流成型的影响,获得了相对较优的装药长径比。杨世全等[14-15]前期针对某等壁厚球缺型药型罩结构,以数值模拟方式开展了杆式射流成型和对混凝土靶侵彻性能的影响研究,首先分析了起爆直径对最终结果的影响,对射流成型机理进行了初步探索,进而采用正交试验方法,分析了药型罩壁厚、装药高度和起爆直径3个影响因素对射流参数和混凝土靶体的侵彻深度5个评估指标的敏感性,并得到了获得最大侵深的参数组合。

因此,针对同样等壁厚球缺型药型罩结构,采用LS-DYNA3D显示动力学分析软件,就装药长径比对杆式射流成型和对混凝土靶侵彻性能的影响开展进一步研究。结合射流成型理论,从装药爆轰波成长以及爆轰波阵面与药型罩作用的机理层面,分析装药长径比对最终结果的影响,并对射流成型机理进行深入探索。

1 药型罩及装药结构

典型等壁厚球缺型药型罩结构如图1所示,装药结构为圆柱加圆锥台的组合结构,采用装药尾端中心一点起爆方式进行起爆。

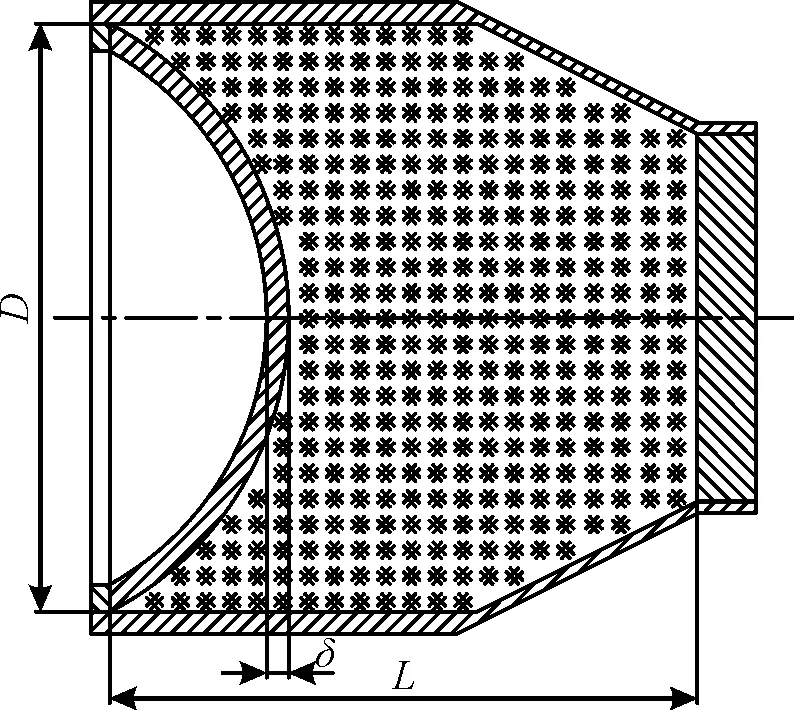
图1 药型罩及装药结构Fig.1 The structure of liner and charge

图中药型罩外圆曲率半径为93 mm,装药圆柱段直径D为160 mm,圆锥台小端面直径为100 mm,药型罩壁厚δ为7 mm,L为装药高度。通过调整装药圆柱段高度使其具有不同装药高度,L与D之比L/D为0.5～1.7,以步长为0.1来确定不同数值模拟方案。

2 数值模拟分析模型

2.1 算法选择及几何模型的建立

在数值模拟研究中,涉及到装药爆轰过程中炸药自身产物膨胀、药型罩压垮和射流成型等复杂大变形问题以及射流和混凝土靶体相互作用,为此采用LS-DYNA3D中的多物质ALE算法和流固耦合方式进行三维数值模拟。药型罩、装药和空气采用欧拉单元,单元采用多物质ALE算法,用以模拟炸药爆轰、药型罩压垮和侵彻体成型过程中物质在单元间的流动;壳体和混凝土靶采用拉格朗日单元,两种单元间采用流固耦合方式来模拟相互间作用。

取结构的1/2进行建模,在对称面上施加对称边界约束,空气域大小取Φ240 mm×2 000 mm,其直径为装药口径的1.5倍,在空气域外边界上施加透射边界以模拟无限空气域。射流对混凝土靶侵彻的数值模型中,统一取炸高为2倍装药口径,同时为减小靶体边界对结果的影响,取靶体尺度为Φ500 mm×1 000 mm。所有模型均采用八节点六面体单元和基本相同的网格尺度及同样的网格划分方式进行网格划分,对混凝土靶,在射流与靶体作用的区域,网格尺度与药型罩及装药结构基本一致,网格尺度为2.5 mm,而在该区域之外采用相对较粗的网格,数值模拟的有限元模型分别如图2和图3所示。对射流成型和射流侵彻混凝土靶的数值模拟,取计算时长分别为0.45 ms和1 ms,步长统一设为1 μs,统计计算结束时的射流相关参数。

图2 射流成型有限元模型Fig.2 Finite element model of jetting forming

图3 射流侵彻混凝土靶体有限元模型Fig.3 Finite element model of jetting penetrating to concrete target

2.2 材料模型及状态方程参数选取

药型罩材料为紫铜,采用J-C模型[16]描述材料在装药爆轰驱动下从低应变率到高应变率下的动态行为,采用GRUNEISEN状态方程[17]描述材料压力和体积应变关系,主要参数采用文献[18]的模型数据。

炸药采用高爆燃烧材料模型模拟炸药爆轰,爆轰过程中化学能释放用燃烧反应率及高能炸药状态方程来控制。采用JWL状态方程描述材料压力、内能和比容的关系[19],主要参数选用文献[20]中PBX-9404-3装药的相关数据。

空气考虑为无黏性理想气体,在冲击膨胀下假设为等熵过程,且符合 律状态方程。采用不计偏应力的NULL模型,用LINEAR_POLYNOMIAL状态方程描述材料压力和体积应变关系[17]。研究中取空气初始密度ρ0=1.225 kg/m3,初始压力P0=1×105Pa,绝热指数γ=1.4。

由于混凝土是一种复杂多孔介质复合材料,具有微观各向异性和宏观各向同性特点,采用JHC模型。模型考虑了大应变、高应变率和高压情况,同时结合损伤理论考虑了当混凝土裂纹出现或压垮后其强度降低的材料行为,主要参数选用文献[21]中模型数据。

3 数值模拟结果及分析

3.1 数值模拟结果

不同装药长径比L/D下,不同时刻的典型射流形态以及计算终止时刻射流侵彻后的典型靶体形态分别如表1和图4所示,计算终止时刻杆式射流相关参数和对靶体的侵彻深度X如表1所示。表中vj、vt和Δv分别为射流头部、尾部和头尾速度差;有效射流长度l为去掉射流尾裙部分的实体长度;射流长径比l/d为射流有效长度与其平均直径之比,其平均直径为在射流长度上每隔2 mm取一点,得到该点处的射流直径,通过不同点处射流直径得到整个射流的平均直径;射流直径均方差σ表示射流均匀程度,其值越小,表示射流越均匀,其计算公式为:

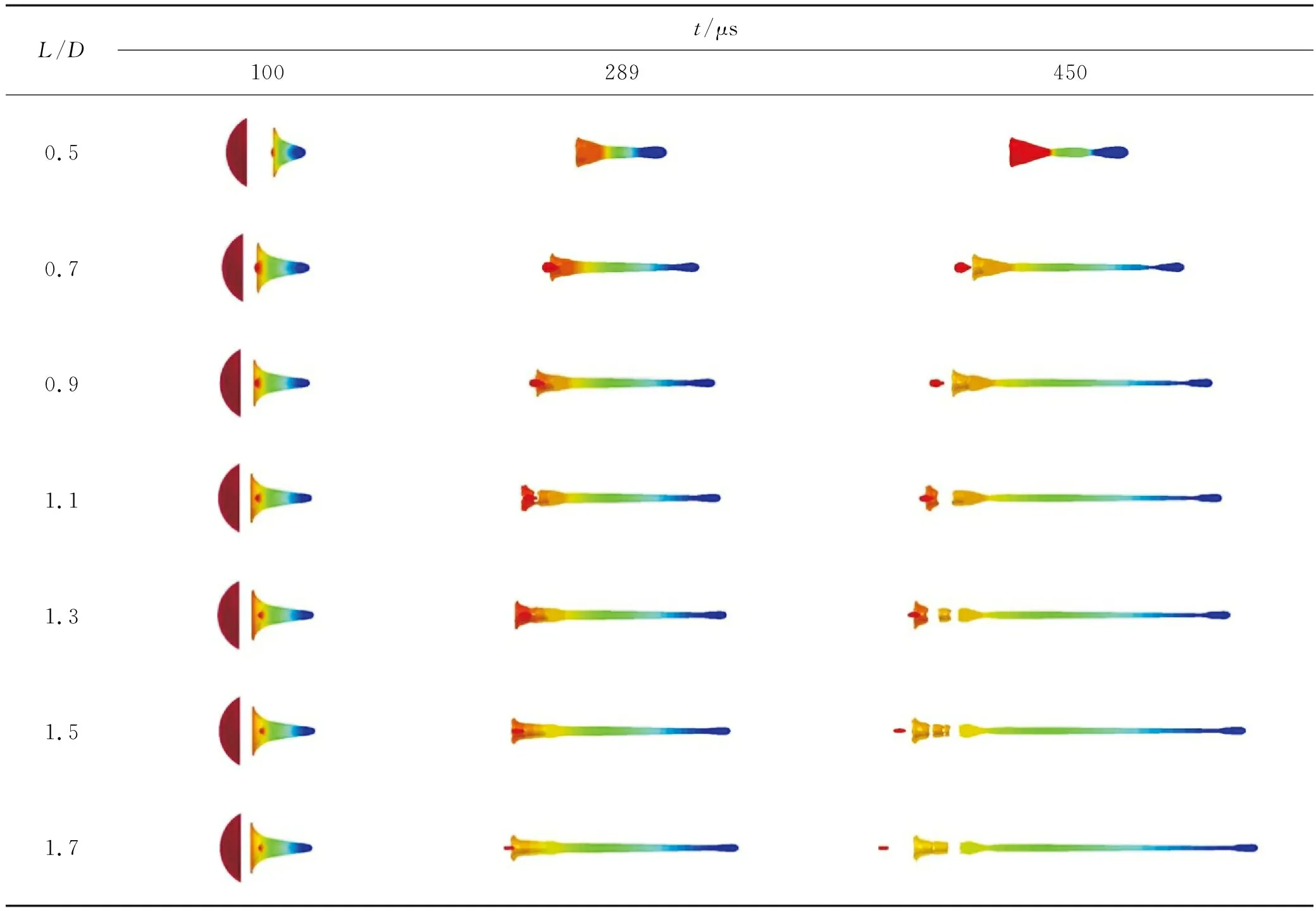
表1 不同时刻的杆式射流形态Table 1 The JPC shapes at different moments

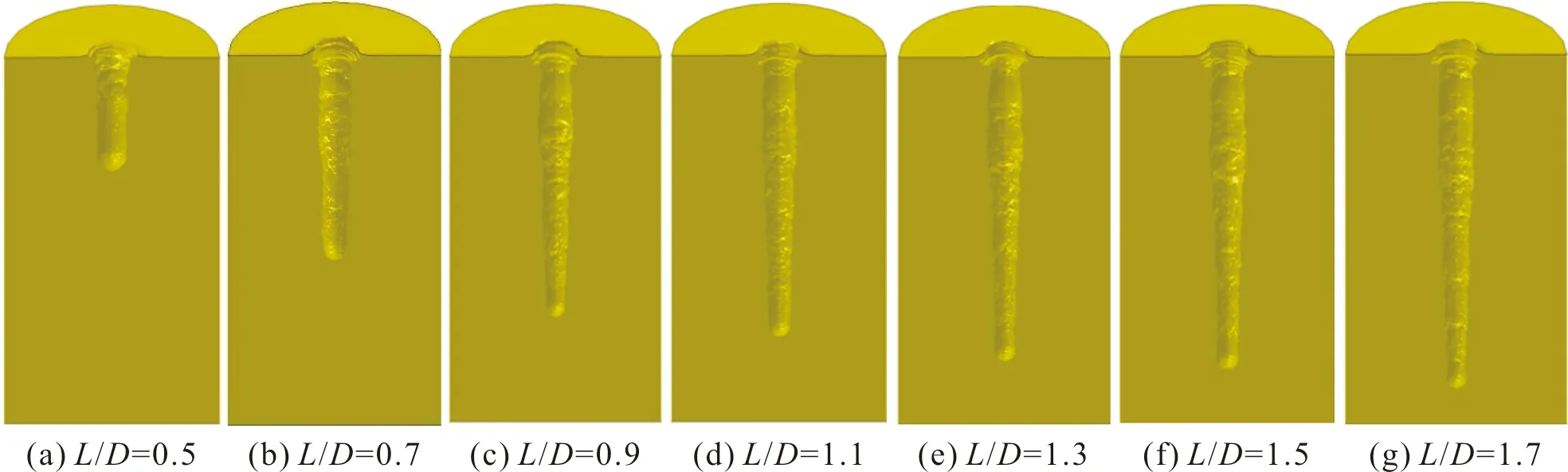
图4 计算终止时刻射流侵彻后的靶体形态Fig.4 The target shapes after JPC penetrating at numeration terminate time

(1)

式中,d为射流长度上不同点处射流直径di(i=1,2,…,n)的平均值。

表2和图5为射流速度、长度和对混凝土靶体的侵彻深度随装药长径比的变化关系。由结果可看出:随着装药长径比的增大,在计算终止时刻的射流头尾部速度以及头尾速度差更大,最终形成的有效射流长度也越长,对靶体的侵彻深度也越大,各结果的增加幅度均随装药长径比的增大而逐渐减小。

表2 计算终止时刻杆式射流参数和侵彻深度Table 2 The JPC parameters and penetrating depth at numeration terminate time

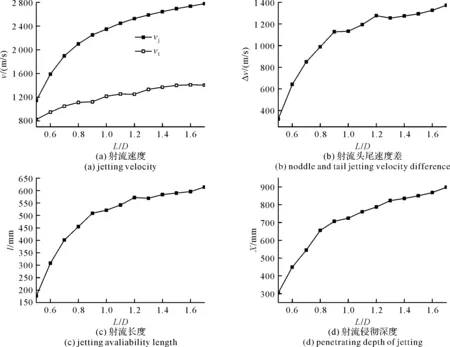
图5 射流参数和侵彻深度随L/D的变化关系Fig.5 The variety relation between the jetting parameters and penetrating depth with L/D

图6进一步给出了射流长径比和直径均方差随装药长径比的变化关系。由结果可看出:射流长径比随装药长径比的增大而增大,直径均方差随装药长径比的增大而减小,其增大和减小的幅度均随装药长径比的增大而逐渐减小,同时射流长径比的增大对应着其直径均方差的减小,表明射流长径比越大时,形成的射流越均匀,与图4所示不同装药长径比下的射流形态相符。

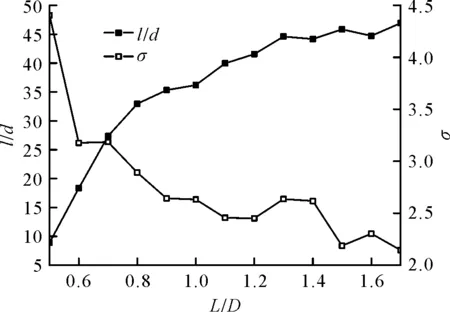
图6 射流长径比和直径均方差随L/D的变化关系Fig.6 The variety relation between the length-to-diameter and diameter standard deviation of jetting with L/D

3.2 结果分析

依据射流成型理论[20],射流头部速度vj的表达式为:

(2)

式中:v0为罩微元压合速度;β,α,δ分别为压合角、锥角和偏转角;对于确定的药型罩,α为一给定值,射流速度就与罩微元压合速度、压合角和偏转角相关。

由式(2)可知,要获得更高的射流速度,需要获得更高的药型罩微元压合速度v0,同时需尽可能降低罩微元偏转角δ,以降低罩微元压合角β,这就需要装药起爆后在药型罩上能获得更高的作用压力,同时还需有较好的爆轰波形,以降低爆轰波阵面与药型罩顶面间的夹角。

数值模拟进一步给出了不同装药长径比下,图7为装药爆轰波到达药型罩端面时刻的爆轰波形以及最终作用到药型罩上的压力以及不同装药长径比下的装药质量M与初始装药长径比下装药质量M0之比值随装药长径比的变化关系,如图8所示。

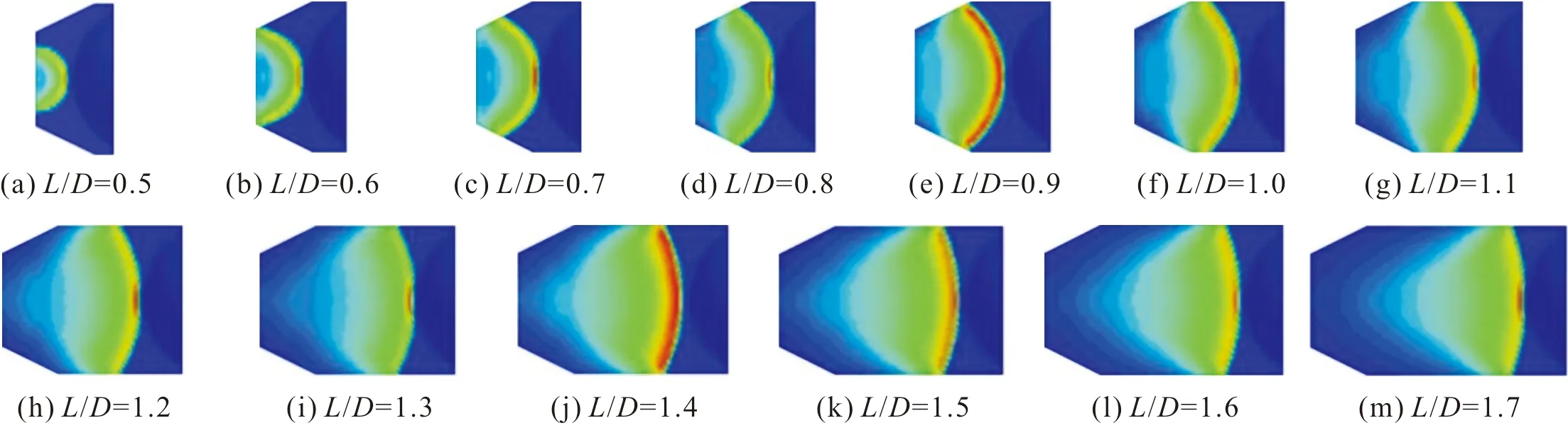
图7 不同L/D下爆轰波到达药型罩端面时刻的爆轰波形Fig.7 The charge detonation wave shape at detonation wave arriving to liner head face under different L/D

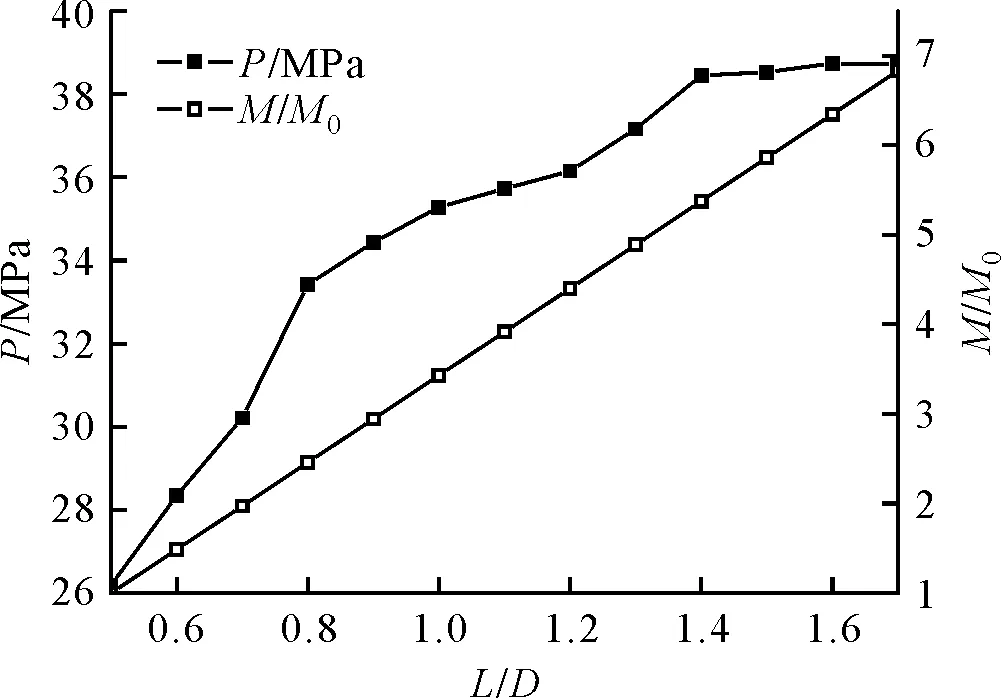
图8 作用到药型罩上的压力与和装药质量比随L/D的变化关系Fig.8 The variety relation between the pressure acting on liner, mass ratio of charge and L/D

由结果可看出,在研究中的起爆方式下,装药起爆后形成一球面爆轰波,当其到达药型罩顶端时,爆轰波与药型罩的接触面为一球面。随着装药长径比的增大,装药爆轰波的成长越充分,其到达药型罩顶端时形成球面爆轰波的半径也越大,爆轰波阵面与药型罩外壁的夹角也越小相应作用到药型罩表面的有效压力也越大从而进一步增大了药型罩的压垮速度并有效减小了压合角,也越有利于射流成型,使形成的射流具有更高速度,形成有效射流的长度也更长,对靶体的侵彻深度也相应更大。

从图7的结果还可看出,随着装药长径比的增大,最终爆轰波阵面与药型罩外壁夹角减小的幅度也逐渐降低,反应到图8中作用到药型罩上压力的增大幅度也逐渐减弱,即随着装药长径比增大,其对作用到药型罩上压力增大的贡献逐渐减弱。

从图8可看出,装药质量比随其长径比呈线性递增,在装药长径比由0.5增加到0.9时,装药爆轰作用到药型罩上的压力由26.19 MPa增加到34.43 MPa,而装药质量比则由1增加到2.94,前者增加的比率为20.60,显著高于后者增加的比率4.86,即药型罩上的压力增加幅度显著高于装药质量比增加幅度,此时射流头尾速度、头尾速度差、有效长度和对靶体的侵彻深度都显著增加,其增幅分别达到了96.59%、36.23%、251.89%、188.13%和131.37%,其中射流有效长度和对靶体的侵彻深度更是成倍的增长,即此时装药长径比的增加对射流成型的贡献较明显。在装药长径比由0.9增加到1.4时,装药爆轰作用到药型罩上的压力由34.43 MPa增加到38.45 MPa,而装药质量比由2.94增加到5.37,前者增加的比率为8,明显小于装药长径比由0.5增加到0.9时,亦略高于后者增加的比率4.86,此时最终获得的射流头尾速度、头尾速度差、有效长度和对靶体侵彻深度的增幅仅为17.41%、21.9%、12.95%、14.71%和18.22%,其中射流有效长度和对靶体的侵彻深度增幅不到20%,即装药长径比的增加对射流成型的贡献已逐渐微弱。而当装药长径比由1.4增加到1.7时,装药爆轰作用到药型罩上的压力由38.45 MPa增加到38.72 MPa,而装药质量比由5.37增加到6.83,前者增加的比率仅为0.9,显著低于后者增加的比率4.86,此时最终获得的射流头尾速度、头尾速度差、有效长度和对靶体侵彻深度的增幅仅为5.11%、2.59%、7.81%、5.13%和7.53%,均远小于10%,即装药长径比的增加对射流成型的贡献已非常微弱。这与图8得出的在装药长径比为1.4时,作用到药型罩上的爆轰波阵面已趋近于平面,此时进一步增大装药长径比对射流成型的贡献已非常微弱结果相符,分析结论也与文献[11-13]的结论相符。

综上所述,在装药长径比由0.5增加到0.9时,增加装药长径比可显著提高射流性能,随着装药长径比的进一步增加,其对射流成型的贡献逐渐减弱,当装药长径比高于1.4时,增大装药长径比对射流成型已基本没有贡献,只会显著增大战斗部装药空间和质量。综合考虑战斗部质量、空间和射流威力,战斗部装药长径比不宜超过1.4,在受限战斗部质量和空间,且为中心一点起爆条件下,可优选装药长径比为0.9或1.0。

4 结论

针对某等壁厚球缺型药型罩结构,基于ANSYS/LS-DYNA3D显示动力学分析软件,采用多物质ALE算法和流固耦合方式,较好地模拟了不同条件下装药爆轰波的成长及射流成型过程,分析了装药长径比对杆式射流成型和对混凝土靶体侵彻性能的影响,并对杆式射流成型机理进行了初步探索,得到主要结论:

1)随着装药长径比的增大,装药爆轰波的成长越充分,其到达药型罩顶端时形成球面爆轰波的半径也越大,爆轰波阵面与药型罩外壁的夹角也越小,相应作用到药型罩表面的有效压力也越大,也越有利于射流的成型,对靶体的侵彻深度也相应更大。

2)在装药长径比由0.5增加到0.9时,作用到药型罩上的压力的增加幅度显著高于装药质量增加幅度,增加装药长径比可显著提高射流性能;当装药长径比超过1.0时,作用到药型罩上的压力的增加幅度明显低于装药质量增加幅度,此时装药长径比的增加,对射流成型的贡献逐渐减弱,在装药长径比为1.4时,作用到药型罩上的爆轰波阵面已趋近于平面,此时进一步增大装药长径比对射流成型已非常微弱。

3)综合考虑战斗部质量、空间和射流威力,战斗部装药长径比不宜超过1.4,在受限战斗部质量和空间,且为中心一点起爆条件下,可优选装药长径比为0.9或1.0。