融合卷积神经网络和最短路径计算的染色体三维重构

赵凤娇,钟 诚

(广西大学 计算机与电子信息学院,南宁 530004)(广西高校并行分布式计算技术重点实验室,南宁 530004) E-mail：1913392073@st.gxu.edu.cn

1 引 言

越来越多的研究表明,基因组的结构和功能是相互统一的,染色体的三维结构对基因表达调控等多种细胞功能非常重要,重建染色体的三维结构对研究基因活动的潜在机制具有重要意义[1].染色体构象捕获(3C)技术[2],特别是与新一代测序技术结合的高通量染色体构象捕获(Hi-C)技术[3],为染色体三维结构的研究提供了全基因组的基因位点相互作用频率(IF)数据.

目前已有不少方法使用Hi-C数据进行染色体三维重构,其中一些是基于距离约束实现的方法[4].文献[5]建立了一个概率模型,由Hi-C数据确定空间距离,然后使用马尔可夫链蒙特卡罗方法从数据中生成一个代表性样本,以重建染色体三维结构.文献[6]将染色体三维重构表述为半定规划问题,并利用黄金分割法确定出将IF值转换为空间距离的合适参数,以实现重建染色体的三维结构.文献[7]通过泊松分布计算IF与空间距离之间的关系,采用多模型预测控制方法推断染色体三维结构.以上几种方法可以重建出质量相对较好的染色体三维结构,然而由于算法模型的复杂性,它们只能有效处理几百个基因位点大小的IF矩阵,无法处理更高分辨率的IF数据.文献[8]使用基于构象能量和流形学习的方法来预测染色体的三维结构.文献[9]将多维缩放(MDS)方法[10]与高斯公式推断的相邻基因位点局部相关性相结合,从染色体的IF矩阵中推断出染色体三维结构.文献[11]利用贝叶斯理论[12]定义染色体三维结构空间的条件概率分布,使用分层优化策略找出满足给定约束条件下概率最高的染色体三维结构.ShRec3D方法[13]使用最短路径算法预处理填充稀疏的IF矩阵,然后使用MDS方法重建染色体的三维结构.MDSGA方法[14]改进了ShRec3D算法,使用遗传算法优化最短路径推断的距离,然后使用MDS方法重构染色体三维结构.虽然与ShRec3D算法相比,MDSGA方法提高了重构的三维结构的精度,然而大大增加了算法所需的时间.

卷积神经网络(CNN)是深度学习的主流模型之一,已在图像处理、计算机视觉和自然语言处理等领域得到广泛应用[15].为了在高分辨率染色体数据上有效重构出精度更高的染色体三维结构,本文研究提出一种融合CNN和最短路径计算的染色体三维重构方法.余下的第2节详细阐述重构算法;第3节给出本文算法和同类具有代表性算法在Hi-C数据上的实验结果;第4节总结本文的工作并给出下一步研究方向.

2 方 法

本文将Hi-C技术产生的染色体相互作用频率(IF)数据构成一个n×n规模的矩阵A,其中n代表基因位点的数量,矩阵元素Aij保存的是第i个基因位点和第j个基因位点之间的IF值.Hi-C实验得到的IF数据组成的矩阵常常是稀疏的[16],为了提高染色体三维重构精度,首先需要降低IF矩阵的稀疏程度.为此,本文首先通过CNN建模,将原始稀疏IF矩阵推断形成相对稠密IF矩阵,然后将相对稠密IF矩阵转换为距离矩阵,依据距离矩阵构造加权无向图,并计算图中任意两顶点之间的最短距离,在此基础上运用多维缩放方法在完整距离矩阵上实现染色体三维重构.下面详细阐述本文给出的融合卷积神经网络和最短路径计算的染色体三维重构方法.

2.1 推断相对稠密IF矩阵

为了从染色体的原始IF矩阵推断出相对稠密IF矩阵,本文构建的CNN模型在训练中将原始IF矩阵作为已知的相对稠密IF矩阵,将使用随机下采样方法处理原始IF矩阵得到的结果作为稀疏IF矩阵.

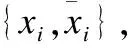
(1)

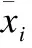
本文参考文献[15]搭建CNN框架,所构建的染色体三维重构CNN框架由3种不同类型的卷积层组成,具体结构如图1所示.

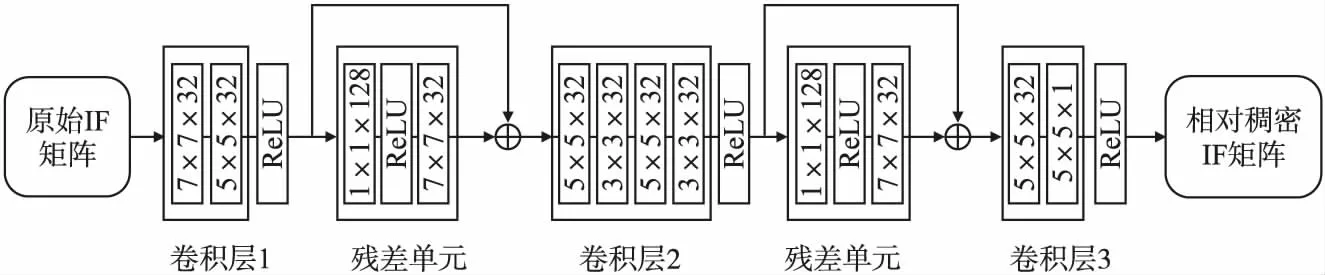
图1 染色体三维重构的卷积神经网络模型框架Fig.1 Convolution neural network model framework for 3D chromosome reconstruction

图1中CNN框架的第1层用于提取和表示染色体稀疏IF矩阵上的特征,第2层用于调整矩阵的大小,第3层用于将提取到的特征非线性映射到相对稠密IF矩阵上,然后输出推断结果.CNN框架中的修正线性单元(ReLU)用于非线性激活函数,残差单元用于防止随着网络深度的增加,出现退化现象.

本文使用Tensorflow实现CNN模型,权重参数根据Xavier初始化方法进行初始化,使用随机梯度下降法对卷积核权值进行更新.

2.2 推断完整距离矩阵

染色体IF矩阵的大部分有效数据都集中在矩阵对角线附近,而偏离对角线的远距离数据则几乎没有.虽然使用CNN建模可以很好地推断出染色体IF矩阵中对角线附近的缺失值,但是偏离对角线的远距离位置的数据依然很稀疏.为此,本文将相对稠密IF矩阵转换为距离矩阵,然后通过最短路径算法计算得到染色体的完整距离矩阵.

IF矩阵中的相互作用频率越大,两个对应的基因位点间的欧氏距离就越小.设Bn×n表示相对稠密IF矩阵,其中Bij代表第i个基因位点和第j个基因位点间的IF值;Cn×n表示矩阵B对应的距离矩阵,其中Cij代表第i个基因位点和第j个基因位点间的欧氏距离;i=1,2,…,n,j=1,2,…,n.本文通过翻转相对稠密IF矩阵得到距离矩阵：

(2)

当Bij为0时,表示第i个基因位点和第j个基因位点之间的IF数据缺失,此时Bij对应的Cij为未知距离,用-1表示.距离矩阵对角线元素的值表示某个基因位点和自身之间的距离,其值为0.

若距离矩阵中某一行或某一列除对角线外其余位置的元素值都为-1,则表示Hi-C实验没有收集到该行或该列对应基因位点的有效数据,这样的基因位点对染色体三维重构没有帮助,因此将它的数据从矩阵中移除.本文使用移除无效数据后得到的距离矩阵构建加权无向图,距离矩阵中的基因位点作为图的顶点,两个基因位点之间的距离作为图中对应顶点之间边的权值.若两个基因位点之间的距离值为-1,则图中对应顶点间无边.初始时,若两个顶点vi和vj之间有边,则以边的权值作为vi和vj之间的最短路径长度;若它们之间无边,则其最短路径长度为∞.然后利用最短路径算法求解更新任意一对顶点vi和vj之间的最短路径,i=1,2,…,m,j=1,2,…,m,m≤n.本文将两两顶点之间的最短路径长度作为对应基因位点在三维结构中的欧氏距离,以推断出染色体的完整距离矩阵.

2.3 推断染色体三维结构

获得染色体的完整距离矩阵后,本文使用多维缩放(MDS)方法进行染色体三维重构.MDS方法可以将数据样本从高维空间转换到低维空间,同时确保低维空间中任意两个样本之间的欧氏距离与对应高维空间中的欧氏距离尽可能的相等.设染色体的完整距离矩阵为Dm×m,其中Dij代表第i个基因位点和第j个基因位点之间的距离,重构的染色体结构三维坐标矩阵为F3×m,其中F·i代表第i个基因位点的三维坐标(F1i,F2i,F3i);F·j代表第j个基因位点的三维坐标(F1j,F2j,F3j),则矩阵F和矩阵D中的元素值应尽可能满足以下约束条件：

Dij=‖F·i-F·j‖

(3)

‖F·i-F·j‖表示F·i和F·j之间的欧氏距离.

设S为F的内积矩阵,即S=FTF,由式(3)可以推导得到矩阵S和矩阵D满足如下关系[10]：

(4)

求出Sij之后,i=1,2,…,m,j=1,2,…,m,进而求解S的3个最大的特征值λ1、λ2、λ3以及对应的3个特征向量X1、X2、X3,构成对角矩阵Λ=diag(λ1,λ2,λ3)和特征向量矩阵X=(X1,X2,X3),则可以求出染色体结构的三维坐标矩阵F=Λ1/2XT.推断出三维坐标矩阵F后,即可使用绘图工具绘制出染色体的三维结构.

2.4 算法描述

算法1形式描述了本文给出的融合卷积神经网络和最短路径计算的染色体三维重构算法(简记为CS3dC算法).

算法1.CS3dC

输入：Hi-C数据矩阵Hl×l;染色体原始IF矩阵An×n,l、n为矩阵中染色体基因位点的数量

输出：染色体三维坐标矩阵F3×m,m为有矩阵中染色体效基因位点的数量

Begin

1.从染色体Hi-C数据集中学习染色体IF矩阵的特征,训练出具有利用IF矩阵元素值推断出其邻近区域元素值能力的CNN模型;

2.使用CNN模型根据染色体原始IF稀疏矩阵An×n推断形成相对稠密矩阵Bn×n;

3. fori=0 ton-1 do //从矩阵B计算距离矩阵C

4. forj=0 ton-1 do

5. ifi=jthen

6.C[i][j]←0; //距离矩阵对角线值为0

7. else ifB[i][j]>0 then

8.C[i][j]←1/B[i][j];

9. else

10.C[i][j]←(-1);

11. end if

12. end for

13.end for

14.fori=0 ton-1 do //移除距离矩阵C中无效的行和列

15. is_empty←True;

16. forj=0 ton-1 do

17. ifC[i][j]>0 then

18. is_empty←False;

19. break;

20. end if

21. end for

22. if is_empty=True then

23. 移除矩阵C的第i行和第i列;

24. end if

25.end for

26.fork=0 tom-1 do //推断出完整距离矩阵D

27. fori=0 tom-1 do

28. forj=0 tom-1 do

29. ifD[i][j]>C[i][k]+C[k][j]then

30.D[i][j]←C[i][k]+C[k][j];

31. end if

32. end for

33. end for

34.end for

38.fori=0 tom-1 do //计算内积矩阵S的值

39. forj=0 tom-1 do

41. end for

42.end for

43.解方程|S-λE|=0,获得矩阵S的3个最大的特征值λ1、λ2和λ3,构成对角矩阵Λ=diag(λ1,λ2,λ3);

44.将λ1、λ2和λ3代入线性方程(Sx-λx)=0,解得特征向量X1、X2和X3,组成特征向量矩阵X=(X1,X2,X3);

45.计算三维坐标矩阵F=Λ1/2XT;

End

算法CS3dC的步1用于训练CNN模型,所需时间为O(n2);步2使用CNN模型推断相对稠密矩阵Bn×n,所需时间为O(n2);步3～步13使用相对稠密矩阵B计算出距离矩阵Cn×n,所需时间为O(n2);步14～步25用于找出并移除距离矩阵C中无效的行和列,所需时间为O(n2);步26～步34执行从距离矩阵Cm×m推断得到完整距离矩阵Dm×m,所需时间为O(m3);步35所需时间为O(m2),步36和步37所需时间均为O(m);步38～步42计算内积矩阵S的值,所需时间为O(m2);步43和步44所需时间均为O(m2);步45计算三维坐标矩阵F,所需时间为O(m2).因此,算法CS3dC的时间复杂度为O(n2+m3)=O(n3),m≤n.算法CS3dC运行过程中使用染色体Hi-C数据矩阵Hl×l、原始IF矩阵An×n、相对稠密矩阵Bn×n、距离矩阵Cn×n、完整距离矩阵Dm×m、内积矩阵Sm×m以及三维坐标矩阵F3×m,因此算法所需的空间复杂度为O(l2+n2+m2+m)=O(l2+n2),m≤n.

本文算法CS3dC通过融合卷积神经网络和最短路径计算从染色体原始IF矩阵推断出完整距离矩阵,降低了染色体矩阵的稀疏程度,减少了使用MDS算法重构染色体三维过程中不确定值的数量,从而提高了重构结果的精度.

3 实 验

实验在广西大学Sugon 7000A超级并行计算机系统(1)https：//hpc.gxu.edu.cn/上进行,使用CX50-G30计算节点,其CPU为2×Intel Xeon Gold 6230,共40核,配置192GB DDR4内存,操作系统为64位版本的CentOS 7.4,采用Python3.7编程实现算法.

本文使用的实验数据来自高通量基因表达数据库(2)https：//www.ncbi.nlm.nih.gov/geo/中登记号为GSE63525的数据集,该数据集中包含多种不同类型细胞的Hi-C相互作用频率矩阵数据[17].本文选用规模为342.46MB的人类B淋巴细胞数据集GM12878中的1～17号染色体数据作为CNN建模的训练集,18号染色体数据作为验证集,19～22号染色体数据作为测试集;选用规模为342.43MB的人类红白血病细胞K562数据集、规模为342.46MB的人类胚肺成纤维细胞IMR90数据集和规模为260.55MB的小鼠B淋巴细胞CH12-LX数据集测试算法的染色体三维重构效果.以上所有数据集分辨率均为100Kb,比对质量(MAPQ)≥30.

实验测试了本文算法CS3dC与具有代表性的同类算法ShRec3D[13]、MDSGA[14]的均方根误差值(RMSE)、Pearson相关系数值(PCC)和所需的运行时间,其中RMSE值越小、PCC值越大,则说明重建得到的染色体三维结构与真实结构越接近,重建效果越好.

3.1 训练卷积神经网络的实验

本文参照文献[18]的设置方式,将CNN训练的随机下采样比率设置为1/16、稀疏IF矩阵子矩阵规模的参数p设置为40、相对稠密IF矩阵子矩阵规模的参数q设置为28.本文设置CNN训练的学习率为0.001,每次处理的样本大小为256,最大训练次数为200,当达到最大训练次数或者验证集上的损失不再发生变化时停止训练.

本文使用Pearson相关系数值(PCC)作为CNN模型训练效果的测试指标,CNN训练过程中验证集上的的损失值(Loss)和PCC值变化情况如图2所示.

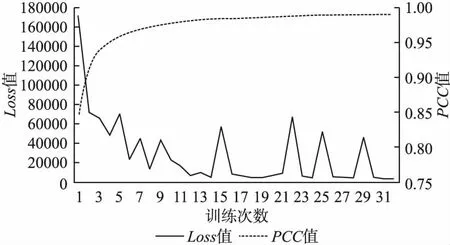
图2 CNN在验证集上的Loss值和PCC值Fig.2 Lossand PCCof CNN on the validation set

由图2可知,随着训练次数的增加,验证集上的Loss值先是急剧下降,然后下降趋势变缓,在下降过程中有降有升,但总体趋势是下降;验证集上的PCC值先是快速增大,然后增速变缓,最终趋近于1.这表明在训练过程中,开始时CNN的收敛速度很快,模型的训练效果也有很大的提升,然后CNN的收敛速度降低,模型的训练效果提升也变得缓慢,最终CNN停止收敛,此时CNN模型的训练效果也达到最佳.

本文将训练好的CNN模型应用到染色体三维重构中,用于从染色体稀疏的原始IF矩阵中推断相对稠密IF矩阵.

3.2 人类细胞数据集上的实验

表1 算法在K562数据集上运行得到的RMSE值和PCC值Table 1 RMSEand PCCobtained by running three algorithms on K562 data set

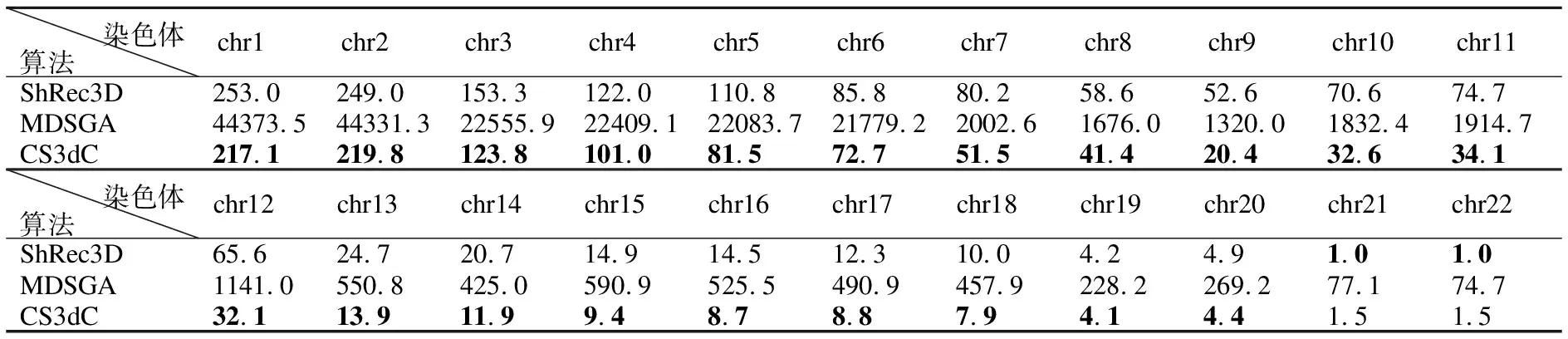
表2 算法在K562数据集上运行所需的时间(s)Table 2 Required time(s) of running three algorithms on K562 data set

首先测试算法ShRec3D、MDSGA和本文算法CS3dC在人类红白血病细胞K562数据集上的RMSE值、PCC值和所需的运行时间,实验结果分别如表1和表2所示.

表1表明,对于K562数据集的1～22号染色体,本文算法CS3dC获得的RMSE值最低,算法MDSGA的RMSE值次之,算法ShRec3D的RMSE值最高;对于K562数据集的1～22号染色体,本文算法CS3dC的PCC值最大,算法ShRec3D的次之,算法MDSGA的最小.这是因为算法ShRec3D仅使用最短路径方法推算距离矩阵中的缺失值,算法MDSGA使用遗传算法进一步优化距离矩阵中的最短路径距离,而本文算法CS3dC融合卷积神经网络和最短路径计算推断完整距离矩阵,从而使得完整距离矩阵中的数据有更高的精度,进而在染色体三维重构过程中始终能够获得更低的RMSE值和更大的PCC值.

由表2可知,在3种算法中,对于K562数据集的1～20号染色体,本文算法CS3dC的运行时间最少;对于20～22号染色体,算法ShRec3D运行时间最少,其次是本文算法CS3dC的运行时间,算法MDSGA的运行时间最多.从整体上看,本文算法CS3dC的运行时间平均值最少,为50.0秒;算法ShRec3D的运行时间平均值次之,为67.5秒;算法MDSGA的运行时间平均值最多,达到8686.8秒.

为了进一步测试算法在其他人类细胞数据集上运行的性能,实验比对了算法ShRec3D、MDSGA和本文算法CS3dC在人类胚肺成纤维细胞IMR90数据集上的RMSE值、PCC值和所需的运行时间,结果如表3和表4所示.

从表3可以看到,本文算法CS3dC的RMSE值在所有染色体上都显著低于其他两种算法MDSGA和ShRec3D;与算法MDSGA和ShRec3D相比,本文算法CS3dC的PCC值更大.这表明在IMR90数据集上仍然是本文算法CS3dC的染色体三维重构效果最好,与真实情况最接近.

表3 算法在在IMR90数据集上运行得到的RMSE值和PCC值Table 3 RMSEand PCCobtained by running three algorithms on IMR90 data set

表4 算法在IMR90数据集上所需的运行时间(s)Table 4 Required time(s) of running three algorithms on MR90 data set

表4的结果表明,对于IMR90数据集的1～17号染色体,本文算法CS3dC所需的运行时间最少,算法ShRec3D的次之,MDSGA的最多;对于18～22号染色体,算法ShRec3D所需的运行时间最少,本文算法CS3dC的次之,算法MDSGA的最多.对于1～22号染色体,本文算法CS3dC的运行时间平均值最低,为49.1秒;算法ShRec3D的运行时间平均值次之,为58.9秒;算法MDSGA的运行时间平均值最多,高达8708.5秒.

综上所述,无论是在K562数据集上还是在IMR90数据集上,本文算法CS3dC都能够在所需运行时间平均值最少的情况下,获得比算法ShRec3D和MDSGA更好的染色体三维重构效果.

3.3 小鼠B淋巴细胞数据集上的实验

为了测试算法在其他不同物种细胞数据集上的染色体三维结构重构效果,本文使用小鼠B淋巴细胞CH12-LX数据集测试算法ShRec3D、MDSGA和本文算法CS3dC的RMSE值、PCC值和所需的运行时间,实验结果分别如表5和表6所示.

由表5可知,对于CH12-LX数据集的1～19号染色体,本文算法CS3dC获得的RMSE值均是3种算法中最低的,且所有值均小于1,而算法MDSGA和ShRec3D的值均大于1;对于CH12-LX数据集的1～19号染色体,本文算法CS3dC的PCC值一直是3种算法中最高的.这表明,本文算法CS3dC在小鼠物种数据上的染色体三维重构效果明显优于其他2种算法ShRec3D和MDSGA.

表6的结果表明,对于1～15号染色体和17、18号染色体,本文算法CS3dC所需的运行时间最少,对于16、19号染色体,算法ShRec3D所需的运行时间最少.在整个数据集上,本文算法CS3dC的运行时间平均值为35.4秒,算法ShRec3D的运行时间平均值为44.5秒,算法MDSGA的运行时间平均值为2131.6秒.因此,从整体上看,本文算法CS3dC在小鼠B淋巴细胞CH12-LX数据集上所需的运行时间是最少的.

上述结果表明,本文算法CS3dC可以在较短的时间内重构出精度更高的小鼠B淋巴细胞染色体三维结构.

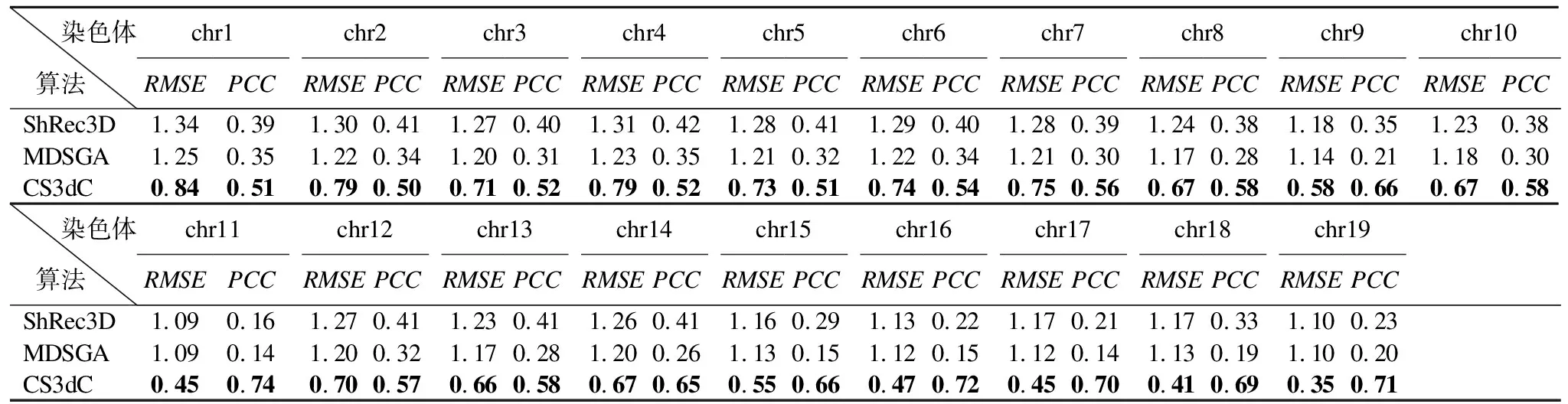
表5 算法在CH12-LX数据集上运行得到的RMSE值和PCC值Table 5 RMSEand PCCobtained by running three algorithgs on CH12-LX data set

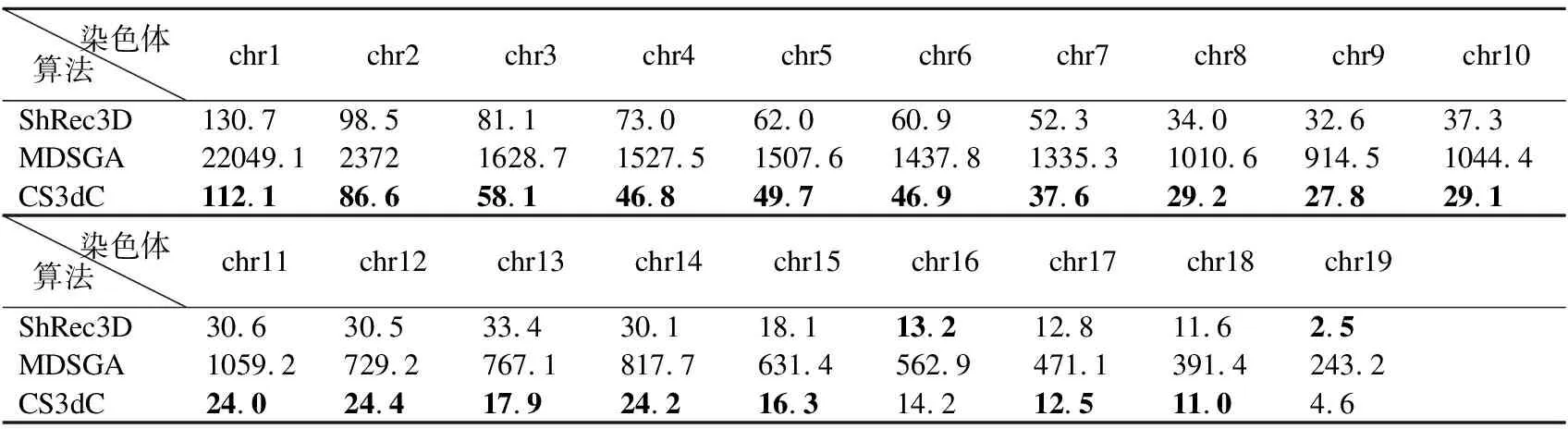
表6 算法在CH12-LX数据集上所需的运行时间(s)Table 6 Required time(s) of running three algorithms on CH12-LX data set

图3 算法重构的染色体三维结构效果Fig.3 Effect of chromosomes 3D structure reconstructed by three algorithms

综合3.2节和3.3节的实验结果可知,与算法ShRec3D和MDSGA相比,本文算法CS3dC不仅可以在人类细胞数据集上也可以在小鼠细胞数据集上,快速地重构出更准确的染色体三维结构.这说明本文提出的融合卷积神经网络和最短路径计算的染色体三维重构算法能够应用于多种物种,具有通用性.

3.4 重构的染色体三维结构可视化

在Hi-C实验中,基因位点倾向于优先与同一拓扑相关结构域(TAD)内的基因位点发生相互作用,这表明同一TAD内的基因位点在染色体三维结构中距离更近[19].本文依据在人类细胞数据集和小鼠细胞数据集上的实验数据结果,使用Python的绘图库Matplotlib绘制染色体的三维结构.以K562的3号染色体、IMR90的10号染色体和CH12-LX的18号染色体为例,算法ShRec3D、MDSGA和本文算法CS3dC重构的三维结构可视化结果如图3所示.

从图3(a)可以看到,K562数据集3号染色体的IF矩阵热图包含两个明显的TAD,本文算法CS3dC重构的染色体三维结构分为两个独立的区域(图中黑线两侧所示);与IF矩阵热图一致,而算法ShRec3D和MDSGA重构的三维结构中的两个部分区分比较模糊(图中黑线两侧所示),没有很好地体现出此染色体结构的特点.

图3(b)表明,IMR90数据集10号染色体的IF矩阵热图由两个TAD组成,本文算法CS3dC重构的染色体三维结构也可以划分为两个结构(图中黑线两侧所示),与IF矩阵热图具有对应关系,而算法ShRec3D和MDSGA重构的三维结构区分度很低,可视化效果较差.

从图3(c)也可以看出,CH12-LX数据集18号染色体的IF矩阵热图包含3个较大的TAD,本文算法CS3dC重构的染色体三维结构分为3个紧密的结构(图中黑线两侧所示),与染色体IF矩阵热图表现出的特征相似,而算法ShRec3D和MDSGA的重构结果难以区分,未能有效表示此染色体的三维结构.

上述结果表明,相比于算法ShRec3D和MDSGA,本文算法CS3dC重构得到的染色体三维结构与染色体的IF矩阵热图具有更好的对应关系,它与真实的染色体三维结构具有更高的一致性.

4 结 语

本文设计的染色体三维结构重构算法的特色和新颖之处是：通过卷积神经网络建模处理染色体稀疏的原始相互作用频率矩阵数据,并融合最短路径计算推断出完整距离矩阵,降低了染色体数据的稀疏程度,然后运用多维缩放方法实现推断出精度更高的染色体三维结构,同时算法所需的运行时间较短,而且能够应用于多种物种的染色体三维重构.下一步的工作方向是探索采用其他机器学习方法,例如强化学习和联邦学习方法,建模处理染色体数据是否能获得更好的三维结构重构效果.