三疑三思三次函数*

贺 旭

浙江省宁波市北仑明港高级中学

1 问题提出

浙江省2021年高中数学教学活动评审比赛的一个环节是说题，题目分为A，B组，给选手的准备时间是40分钟，现场说题15分钟.笔者选取A组一道题进行探究.

已知三次函数f(x)=x3-x,设P0(x0,y0)为函数y=f(x)曲线上异于对称中心的任一点，在点P0处的切线l0交曲线点于点P1，在P1点处的切线l1交曲线于点P2，求三角形P0P1P2的面积S△P0P1P2.

图1

解：对三次函数f(x)=x3-x求导，得f′(x)=3x2-1.

联立

同理求点P2的坐标.

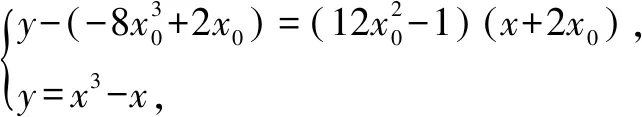
S△P0P1P2的求法有两种：割和补.

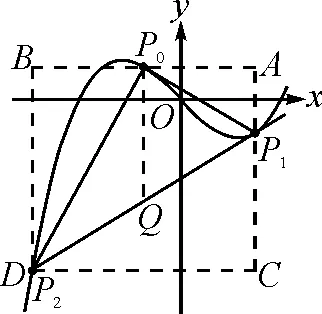
图2

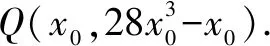
所以S△P0P1P2

法2(补法)：如图2，补出矩形ABCD.

所以S△P0P1P2

=S矩形ABP2C-S△AP0P1-S△BP0P2-S△CP1P2

2 三疑

说题比赛时，选手们主要有3个疑问：①无法求出交点P1，P2；②无法求出三角形面积；③没有将这道题进行推广.

2.1 求交点

对于疑问①，可以直接利用拆项进行因式分解从而求出点P1的横坐标；也可以观察图形，发现直线P0P1与曲线只有两个交点，而方程联立得到的是三次方程，因此必有一个重根，易知重根是x=x0，这样就可以求得另一个根x=-2x0.求点P2时，可以根据点P1的横坐标直接进行迭代，也可以类比点P1的坐标求法，一模一样求一遍.

2.2 求面积

三角形面积的求法常用的有三种：直接法、割法、补法.对这道题而言，运算量最小的是割法，直接法最繁琐，不推荐，补法普适性强，易于推广.现对三角形的面积用补形法进行深入探究.

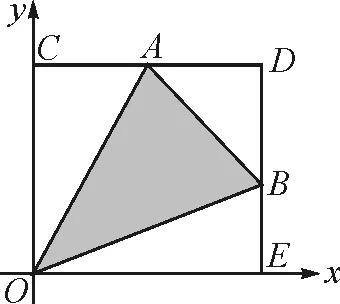
图3

如图3，已知三角形的三个顶点O(0,0),A(x1,y1),B(x2,y2)，求三角形OAB的面积S△OAB.

S△OAB

=S矩形OEDC-S△DAB-S△CAO-S△EBO

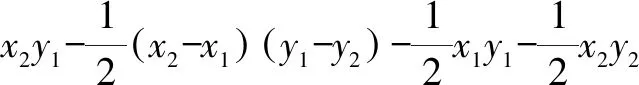
图4

如图4，已知△ABC,A(x1,y1),B(x2,y2),C(x3,y3)，求三角形ABC的面积S△ABC.

任意三角形通过平移都能经过原点，变成图3，这里将图4的A点平移到原点，则

这样就推导出平面内任意三角形的面积公式.

2.3 再推广

已知三次函数f(x)=ax3+bx+c，设P0(x0,y0)为曲线y=f(x)上异于对称中心的任一点，在P0处的切线l0交曲线于点P1，在P1处的切线l1交曲线于点P2，求三角形P0P1P2的面积S△P0P1P2.

解：对三次函数f(x)=ax3+bx+c求导，得f′(x)=3ax2+b.

a(x+2x0)(x-x0)2=0.

所以x1=x0,x2=-2x0，即P1(-2x0,f(-2x0)).用迭代法直接写出P2(4x0,f(4x0)).所以

因此，我们可以发现三角形的面积只与三次函数的三次项系数有关.

3 三思

3.1 且算且思

综合性强的数学题常常难以一眼望穿，需要且算且思，摸着石头过河，边算边想边观察，答案可能在不经意间露出端倪，再通过细细揣摩完善解题过程.本文中在求点P1的横坐标时，有如雾中的感觉，在经历了一系列复杂的运算后，求得x=-2x0，通过迭代的思想就能猜出想点P2的横坐标为x=4x0.踏破铁鞋无觅处，轻松得到点P1，P2的坐标.

3.2 多思少算

三思而后行，做事前多思考，谋定而后动能避免很多麻烦，少走许多冤枉路.高中阶段求面积的方法很多，就公式法来说有三种：

3.3 算后反思

一道题解完后并不代表着结束，而是要反问自己“还有其他方法吗？”“能不能推广到一般情况？”“这道题考查的本质是什么？”通过反思，优化解法，深度理解题意，提升自身素养.对于文中的面积问题，思考如何求平面内任意三角形的面积；将题目中的特殊三次函数换成一般三次函数，又会有什么结论.在不断反问与反思中，探索发现，真可谓：涉浅水者见虾，其颇深者察鱼鳖，其尤甚者观蛟龙[1].